ID3决策树算法及其Python实现_id3可以用基尼指数吗?

一.理论基础

1. 纯度（purity）
对于一个分支结点，如果该结点所包含的样本都属于同一类，那么它的纯度为1，而我们总是希望纯度越高越好，也就是尽可能多的样本属于同一类别。那么如何衡量“纯度”呢？由此引入“信息熵”的概念。

2. 信息熵（information entropy）
假定当前样本集合D中第k类样本所占的比例为pk（k=1,2,…,|y|），则D的信息熵定义为：

             Ent(D) = -∑k=1 pk·log2 pk    （约定若p=0，则log2 p=0）

  显然，Ent(D)值越小，D的纯度越高。因为0<=pk<= 1,故log2 pk<=0，Ent(D)>=0. 极限情况下，考虑D中样本同属于同一类，则此时的Ent(D)值为0（取到最小值）。当D中样本都分别属于不同类别时，Ent(D)取到最大值log2 |y|.
1
2
3

3. 信息增益（information gain）
假定离散属性a有V个可能的取值{a1,a2,…,aV}. 若使用a对样本集D进行分类，则会产生V个分支结点，记Dv为第v个分支结点包含的D中所有在属性a上取值为av的样本。不同分支结点样本数不同，我们给予分支结点不同的权重：|Dv|/|D|, 该权重赋予样本数较多的分支结点更大的影响、由此，用属性a对样本集D进行划分所获得的信息增益定义为：

           Gain(D,a) = Ent(D)-∑v=1 |Dv|/|D|·Ent(Dv)
1

其中，Ent(D)是数据集D划分前的信息熵，∑v=1 |Dv|/|D|·Ent(Dv)可以表示为划分后的信息熵。“前-后”的结果表明了本次划分所获得的信息熵减少量，也就是纯度的提升度。显然，Gain(D,a) 越大，获得的纯度提升越大，此次划分的效果越好。

4. 增益率(gain ratio)
基于信息增益的最优属性划分原则——信息增益准则，对可取值数据较多的属性有所偏好。C4.5算法使用增益率替代信息增益来选择最优划分属性，增益率定义为：

           Gain_ratio(D,a) = Gain(D,a)/IV(a)
1

其中

           IV(a) = -∑v=1 |Dv|/|D|·log2 |Dv|/|D|
1

称为属性a的固有值。属性a的可能取值数目越多（即V越大），则IV(a)的值通常会越大。这在一定程度上消除了对可取值数据较多的属性的偏好。

  事实上，增益率准则对可取值数目较少的属性有所偏好，C4.5算法并不是直接使用增益率准则，而是先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。
1

5. 基尼指数(Gini index)
CART决策树算法使用基尼指数来选择划分属性，基尼指数定义为：

          Gini(D) = ∑k=1 ∑k'≠1 pk·pk' = 1- ∑k=1  pk·pk

  可以这样理解基尼指数：从数据集D中随机抽取两个样本，其类别标记不一致的概率。Gini(D)越小，纯度越高。

  属性a的基尼指数定义：

         Gain_index(D,a) = ∑v=1 |Dv|/|D|·Gini(Dv)

  使用基尼指数选择最优划分属性，即选择使得划分后基尼指数最小的属性作为最优划分属性。
1
2
3
4
5
6
7
8
9

二.代码实现

上传数据集

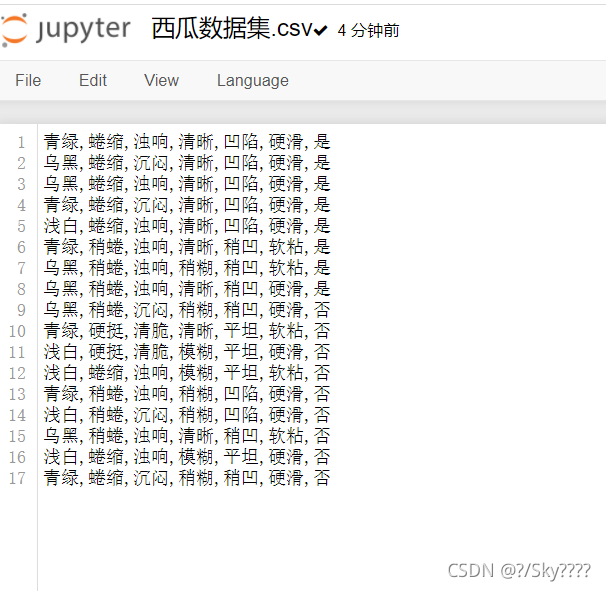
具体代码

import numpy as np
import pandas as pd
import sklearn.tree as st
import math
import matplotlib
import os
import matplotlib.pyplot as plt

data = pd.read_csv('西瓜数据集.csv',header=None)
data


def calcEntropy(dataSet):
    mD = len(dataSet)
    dataLabelList = [x[-1] for x in dataSet]
    dataLabelSet = set(dataLabelList)
    ent = 0
    for label in dataLabelSet:
        mDv = dataLabelList.count(label)
        prop = float(mDv) / mD
        ent = ent - prop * np.math.log(prop, 2)

    return ent

# index - 要拆分的特征的下标
# feature - 要拆分的特征
# 返回值 - dataSet中index所在特征为feature，且去掉index一列的集合
def splitDataSet(dataSet, index, feature):
    splitedDataSet = []
    mD = len(dataSet)
    for data in dataSet:
        if(data[index] == feature):
            sliceTmp = data[:index]
            sliceTmp.extend(data[index + 1:])
            splitedDataSet.append(sliceTmp)
    return splitedDataSet
# 返回值 - 最好的特征的下标
def chooseBestFeature(dataSet):
    entD = calcEntropy(dataSet)
    mD = len(dataSet)
    featureNumber = len(dataSet[0]) - 1
    maxGain = -100
    maxIndex = -1
    for i in range(featureNumber):
        entDCopy = entD
        featureI = [x[i] for x in dataSet]
        featureSet = set(featureI)
        for feature in featureSet:
            splitedDataSet = splitDataSet(dataSet, i, feature)  # 拆分数据集
            mDv = len(splitedDataSet)
            entDCopy = entDCopy - float(mDv) / mD * calcEntropy(splitedDataSet)
        if(maxIndex == -1):
            maxGain = entDCopy
            maxIndex = i
        elif(maxGain < entDCopy):
            maxGain = entDCopy
            maxIndex = i

    return maxIndex


# 返回值 - 标签
def mainLabel(labelList):
    labelRec = labelList[0]
    maxLabelCount = -1
    labelSet = set(labelList)
    for label in labelSet:
        if(labelList.count(label) > maxLabelCount):
            maxLabelCount = labelList.count(label)
            labelRec = label
    return labelRec



def createFullDecisionTree(dataSet, featureNames, featureNamesSet, labelListParent):
    labelList = [x[-1] for x in dataSet]
    if(len(dataSet) == 0):
        return mainLabel(labelListParent)
    elif(len(dataSet[0]) == 1): #没有可划分的属性了
        return mainLabel(labelList)  #选出最多的label作为该数据集的标签
    elif(labelList.count(labelList[0]) == len(labelList)): # 全部都属于同一个Label
        return labelList[0]

    bestFeatureIndex = chooseBestFeature(dataSet)
    bestFeatureName = featureNames.pop(bestFeatureIndex)
    myTree = {bestFeatureName: {}}
    featureList = featureNamesSet.pop(bestFeatureIndex)
    featureSet = set(featureList)
    for feature in featureSet:
        featureNamesNext = featureNames[:]
        featureNamesSetNext = featureNamesSet[:][:]
        splitedDataSet = splitDataSet(dataSet, bestFeatureIndex, feature)
        myTree[bestFeatureName][feature] = createFullDecisionTree(splitedDataSet, featureNamesNext, featureNamesSetNext, labelList)
    return myTree


# 返回值
# dataSet 数据集
# featureNames 标签
# featureNamesSet 列标签
def readWatermelonDataSet():
    dataSet = data.values.tolist()
    featureNames =['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']
    #获取featureNamesSet
    featureNamesSet = []
    for i in range(len(dataSet[0]) - 1):
        col = [x[i] for x in dataSet]
        colSet = set(col)
        featureNamesSet.append(list(colSet))
    
    return dataSet, featureNames, featureNamesSet
# 能够显示中文
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.serif'] = ['SimHei']

# 分叉节点，也就是决策节点
decisionNode = dict(boxstyle="sawtooth", fc="0.8")

# 叶子节点
leafNode = dict(boxstyle="round4", fc="0.8")

# 箭头样式
arrow_args = dict(arrowstyle="<-")


def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    """
    绘制一个节点
    :param nodeTxt: 描述该节点的文本信息
    :param centerPt: 文本的坐标
    :param parentPt: 点的坐标，这里也是指父节点的坐标
    :param nodeType: 节点类型,分为叶子节点和决策节点
    :return:
    """
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)


def getNumLeafs(myTree):
    """
    获取叶节点的数目
    :param myTree:
    :return:
    """
    # 统计叶子节点的总数
    numLeafs = 0

    # 得到当前第一个key，也就是根节点
    firstStr = list(myTree.keys())[0]

    # 得到第一个key对应的内容
    secondDict = myTree[firstStr]

    # 递归遍历叶子节点
    for key in secondDict.keys():
        # 如果key对应的是一个字典，就递归调用
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        # 不是的话，说明此时是一个叶子节点
        else:
            numLeafs += 1
    return numLeafs


def getTreeDepth(myTree):
    """
    得到数的深度层数
    :param myTree:
    :return:
    """
    # 用来保存最大层数
    maxDepth = 0

    # 得到根节点
    firstStr = list(myTree.keys())[0]

    # 得到key对应的内容
    secondDic = myTree[firstStr]

    # 遍历所有子节点
    for key in secondDic.keys():
        # 如果该节点是字典，就递归调用
        if type(secondDic[key]).__name__ == 'dict':
            # 子节点的深度加1
            thisDepth = 1 + getTreeDepth(secondDic[key])

        # 说明此时是叶子节点
        else:
            thisDepth = 1

        # 替换最大层数
        if thisDepth > maxDepth:
            maxDepth = thisDepth

    return maxDepth


def plotMidText(cntrPt, parentPt, txtString):

    """
    计算出父节点和子节点的中间位置，填充信息
    :param cntrPt: 子节点坐标
    :param parentPt: 父节点坐标
    :param txtString: 填充的文本信息
    :return:
    """
    # 计算x轴的中间位置
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    # 计算y轴的中间位置
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    # 进行绘制
    createPlot.ax1.text(xMid, yMid, txtString)


def plotTree(myTree, parentPt, nodeTxt):
    """
    绘制出树的所有节点，递归绘制
    :param myTree: 树
    :param parentPt: 父节点的坐标
    :param nodeTxt: 节点的文本信息
    :return:
    """
    # 计算叶子节点数
    numLeafs = getNumLeafs(myTree=myTree)

    # 计算树的深度
    depth = getTreeDepth(myTree=myTree)

    # 得到根节点的信息内容
    firstStr = list(myTree.keys())[0]

    # 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴（比如说第一次：初始的x偏移量为：-1/2W,计算出来的根节点中心位置为：(1+W)/2W，相加得到：1/2），当前y轴偏移量作为y轴
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)

    # 绘制该节点与父节点的联系
    plotMidText(cntrPt, parentPt, nodeTxt)

    # 绘制该节点
    plotNode(firstStr, cntrPt, parentPt, decisionNode)

    # 得到当前根节点对应的子树
    secondDict = myTree[firstStr]

    # 计算出新的y轴偏移量，向下移动1/D，也就是下一层的绘制y轴
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD

    # 循环遍历所有的key
    for key in secondDict.keys():
        # 如果当前的key是字典的话，代表还有子树，则递归遍历
        if isinstance(secondDict[key], dict):
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            # 计算新的x轴偏移量，也就是下个叶子绘制的x轴坐标向右移动了1/W
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            # 打开注释可以观察叶子节点的坐标变化
            # print((plotTree.xOff, plotTree.yOff), secondDict[key])
            # 绘制叶子节点
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            # 绘制叶子节点和父节点的中间连线内容
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))

    # 返回递归之前，需要将y轴的偏移量增加，向上移动1/D，也就是返回去绘制上一层的y轴
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD


def createPlot(inTree):
    """
    需要绘制的决策树
    :param inTree: 决策树字典
    :return:
    """
    # 创建一个图像
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    # 计算出决策树的总宽度
    plotTree.totalW = float(getNumLeafs(inTree))
    # 计算出决策树的总深度
    plotTree.totalD = float(getTreeDepth(inTree))
    # 初始的x轴偏移量，也就是-1/2W，每次向右移动1/W，也就是第一个叶子节点绘制的x坐标为：1/2W，第二个：3/2W，第三个：5/2W，最后一个：(W-1)/2W
    plotTree.xOff = -0.5/plotTree.totalW
    # 初始的y轴偏移量，每次向下或者向上移动1/D
    plotTree.yOff = 1.0
    # 调用函数进行绘制节点图像
    plotTree(inTree, (0.5, 1.0), '')
    # 绘制
    plt.show()
dataSet, featureNames, featureNamesSet=readWatermelonDataSet()
testTree= createFullDecisionTree(dataSet, featureNames, featureNamesSet,featureNames)
createPlot(testTree)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292

运行结果

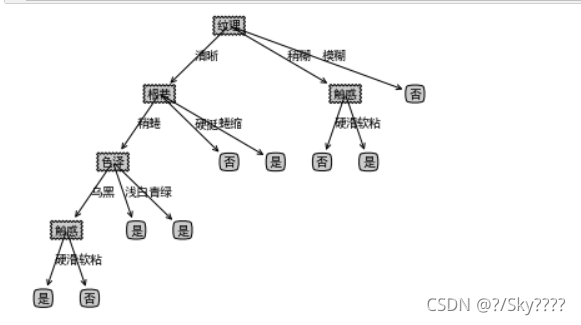
三.用sk-learn库对西瓜数据集，分别进行ID3、C4.5和CART的算法代码实现。

• 决策树的剪枝

剪枝是决策树停止分支的方法之一，剪枝有分预先剪枝和后剪枝两种。预先剪枝是在树的生长过程中设定一个指标，当达到该指标时就停止生长，这样做容易产生“视界局限”，就是一旦停止分支，使得节点N成为叶节点，就断绝了其后继节点进行“好”的分支操作的任何可能性。不严格的说这些已停止的分支会误导学习算法，导致产生的树不纯度降差最大的地方过分靠近根节点。后剪枝中树首先要充分生长，直到叶节点都有最小的不纯度值为止，因而可以克服“视界局限”。然后对所有相邻的成对叶节点考虑是否消去它们，如果消去能引起令人满意的不纯度增长，那么执行消去，并令它们的公共父节点成为新的叶节点。这种“合并”叶节点的做法和节点分支的过程恰好相反，经过剪枝后叶节点常常会分布在很宽的层次上，树也变得非平衡。后剪枝技术的优点是克服了“视界局限”效应，而且无需保留部分样本用于交叉验证，所以可以充分利用全部训练集的信息。但后剪枝的计算量代价比预剪枝方法大得多，特别是在大样本集中，不过对于小样本的情况，后剪枝方法还是优于预剪枝方法的。

1.ID3代码

# 读取西瓜数据集
import numpy as np
import pandas as pd
df = pd.read_table(r'D:/watermelon.txt',encoding='utf8',delimiter=',',index_col=0)
df.head()
# 由于上面的数据中包含了中文汉字，所以需要对数据进一步处理
'''
属性：
色泽 1-3代表 浅白 青绿 乌黑 根蒂 1-3代表 稍蜷 蜷缩 硬挺
敲声 1-3代表 清脆 浊响 沉闷 纹理 1-3代表 清晰 稍糊 模糊
脐部 1-3代表 平坦 稍凹 凹陷 触感 1-2代表 硬滑 软粘
标签：
好瓜 1代表 是 0 代表 不是
'''
df['色泽']=df['色泽'].map({'浅白':1,'青绿':2,'乌黑':3})
df['根蒂']=df['根蒂'].map({'稍蜷':1,'蜷缩':2,'硬挺':3})
df['敲声']=df['敲声'].map({'清脆':1,'浊响':2,'沉闷':3})
df['纹理']=df['纹理'].map({'清晰':1,'稍糊':2,'模糊':3})
df['脐部']=df['脐部'].map({'平坦':1,'稍凹':2,'凹陷':3})
df['触感'] = np.where(df['触感']=="硬滑",1,2)
df['好瓜'] = np.where(df['好瓜']=="是",1,0)
#由于西瓜数据集样本比较少，所以不划分数据集，将所有的西瓜数据用来训练模型
Xtrain = df.iloc[:,:-1]
Xtrain = np.array(Xtrain)
Ytrain = df.iloc[:,-1]
# 调用sklearn内置的决策树的库和画图工具
from sklearn import tree
import graphviz
# 采用ID3算法，利用信息熵构建决策树模型
clf = tree.DecisionTreeClassifier(criterion="entropy")
clf = clf.fit(Xtrain,Ytrain)
# 绘制决策树的图形
feature_names = ["色泽","根蒂","敲声","纹理","脐部","触感"]
dot_data = tree.export_graphviz(clf
,feature_names=feature_names
,class_names=["好瓜","坏瓜"]
,filled=True
,rounded=True
)
graph = graphviz.Source(dot_data)
graph
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

熵和信息增益
设S是训练样本集，它包括n个类别的样本，这些方法用Ci表示，那么熵和信息增益用下面公式表示：
信息熵：

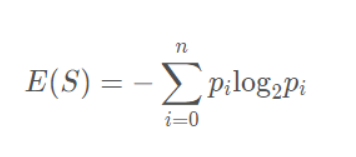
其中pi表示Ci的概率
样本熵：

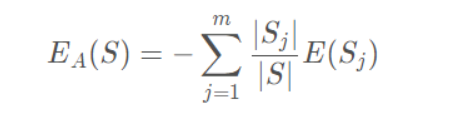
其中Si表示根据属性A划分的S的第i个子集，S和Si表示样本数目
信息增益：

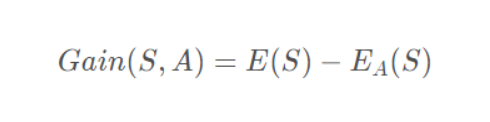
ID3中样本分布越均匀，它的信息熵就越大，所以其原则就是样本熵越小越好，也就是信息增益越大越好。

2.C4.5实现

（1）对比ID3的改进点
C4.5算法是用于生成决策树的一种经典算法，是ID3算法的一种延伸和优化。C4.5算法对ID3算法进行了改进 ，改进点主要有：

用信息增益率来选择划分特征，克服了用信息增益选择的不足，
信息增益率对可取值数目较少的属性有所偏好；
能够处理离散型和连续型的属性类型，即将连续型的属性进行离散化处理；
能够处理具有缺失属性值的训练数据；
在构造树的过程中进行剪枝；
（2）特征选择
特征选择也即选择最优划分属性，从当前数据的特征中选择一个特征作为当前节点的划分标准。 随着划分过程不断进行，希望决策树的分支节点所包含的样本尽可能属于同一类别，即节点的“纯度”越来越高。

（3）信息增益率
信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，C4.5算法采用信息增益率来选择最优划分属性。增益率公式

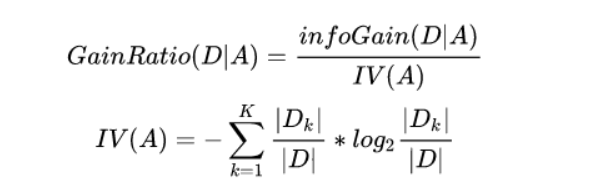
信息增益率准则对可取值数目较少的属性有所偏好。所以，C4.5算法不是直接选择信息增益率最大的候选划分属性，而是先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择信息增益率最高的。
（4）对连续特征的处理
当属性类型为离散型，无须对数据进行离散化处理；

当属性类型为连续型，则需要对数据进行离散化处理。具体思路如下：

（5）剪枝
通过信息增益比计算得到的决策树也需要进行剪枝，剪枝方法同ID3算法。

3.CART算法

CART算法构造的是二叉决策树，决策树构造出来后同样需要剪枝，才能更好的应用于未知数据的分类。CART算法在构造决策树时通过基尼系数来进行特征选择。
对于训练样本集，其基尼指数如下：

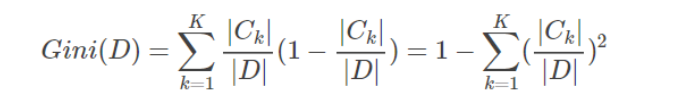
如果样本集合D根据特征Am的取值可以分为两部分D1和D2，那么在特征Am的条件下，D的基尼指数如下：

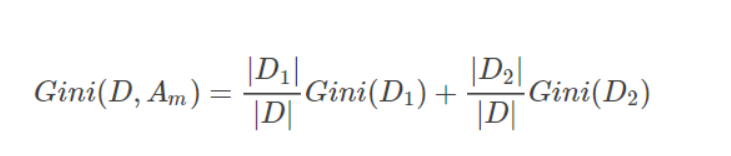
基尼指数Gini(D)表征着数据集D的不确定性，而在特征Am的条件下，D的基尼指数则表征着在特征Am确定的条件下D的不确定性，因此基尼指数之差和信息增益及信息增益比一样，可以表征特征Am对数据集D的分类的能力。
决策树构建

• 输入： 训练数据集D，特征集A，结点样本数阈值δ，基尼指数阈值ϵ
• 输出： CART二叉决策树TT
• step1 若样本特征集为空，则TT是一棵单节点数，其类别为D中样本数最多的类，返回T；否则，转到step2。
• step2
  对数据集D，计算特征集A中所有特征所有可能切分点的基尼指数，若基尼指数的值均小于给定阈值ϵ，则TT是一棵单节点数，其类别为D中样本数最多的类，返回T；否则，转到step3。
• step3
  选择基尼指数最小的特征Amin和相应切分点α作为根节点的特征值和切分标准，根据D中样本是否等于α（或≤α≤α，或≥α≥α）将D分为两个子集D1和D2，将D1和D2分别分配到两个子结点中，若子结点样本数均小于给定阈值δ，则该子结点是一个叶结点，若两个子结点均为叶结点，返回T；否则，返回T并转到step4。
• step4 对于非叶子结点，令D等于该子结点所对应的数据集，特征集A=A−{Amin}，递归的调用step1-step3，返回子树T。
• 输入： CART算法生成的决策树T
• 输出： 最优决策树Tα
• step1 若T为单结点树或由一个根结点和两个叶结点构成的树，返回T；否则，k=0,α0=0,T0=T，转到step2。
• step2
  k=k+1，计算Tk−1所有内部结点t的g(t)值，g(t)的最小值为αk，g(t)取最小值处的结点为tk，剪掉以tk为根结点的子树Ttk，并以tk处类别最多的样本作为新的叶结点tk的类，得到[αk,αk+1)上的最优子树Tk。
• step3 若Tk是由一个根结点和两个叶结点构成的树，转到step4；否则，转到step2。
• step4
  利用验证数据集对最优子树序列T0,T1,⋯,TL进行测试，选择对于验证数据集有最小基尼指数的最优子树作为最终的最优决策树Tα，返回Tα。

总结

了解了ID3，C4.5，CART算法之间的优点和缺点，改进的不同之处。

参考

https://blog.csdn.net/cxq_baby/article/details/97510434，
https://www.cnblogs.com/dennis-liucd/p/7905793.html，
https://icode9.com/content-4-1201589.html