蚁群算法理解与实现_蚁群算法解决图的着色

蚁群算法，也是优化算法当中的一种。蚁群算法擅长解决组合优化问题。蚁群算法能够有效的解决著名的旅行商问题（TSP），不止如此，在其他的一些领域也取得了一定的成效，例如工序排序问题，图着色问题，网络路由问题等等。接下来便为大家简单介绍蚁群算法的基本思想。

蚁群算法，顾名思义就是根据蚁群觅食行为而得来的一种算法。单只蚂蚁的觅食行为貌似是杂乱无章的，但是据昆虫学家观察，蚁群在觅食时总能够找到离食物最近的路线，这其中的原因是什么呢？其实，蚂蚁的视力并不是很好，但是他们又是凭借什么区寻找到距离食物的最短路径的呢？经过研究发现，每一只蚂蚁在觅食的过程中，会在沿途释放出一种叫做信息素的物质。其他蚂蚁会察觉到这种物质，因此，这种物质会影响到其他蚂蚁的觅食行为。当一些路径上经过的蚂蚁越多时，这条路径上的信息素浓度也就越高，其他蚂蚁选择这条路径的可能性也就越大，从而更增加了这条路径上的信息素浓度。当然，一条路径上的信息素浓度也会随着时间的流逝而降低。这种选择过程被称之为蚂蚁的自催化行为，是一种正反馈机制，也可以将整个蚁群认定为一个增强型学习系统。

为了让大家更好的理解上文中提到的蚁群觅食行为，这里通过一张图片来说明蚁群觅食行为。

如图所示，A点为一个蚁穴，设定其中有两只蚂蚁，蚂蚁1和蚂蚁2。B点为食物所在位置，C点只是路径上的一点。假设ABC形成一个等边三角形，且两只蚂蚁的移动速度均相同。

在t0时刻，两只蚂蚁在蚁穴中，在他们面前有两条路可以选择，即AB或AC。两只蚂蚁随机进行选择，我们假设蚂蚁1选择了路径AC，而蚂蚁2选择了路径AB。

在t1时刻是，蚂蚁1走到了C点，而蚂蚁2走到了B点，即食物所在位置。他们在其经过的路径上释放了信息素，在途中用虚线表示。之后蚂蚁2将食物运往蚁穴，此时它有两种选择，走BC或走CA，但是BC上信息素浓度为0，因此选择CA进行原路返回，返回时依然在沿途释放信息素，蚂蚁1则从C点向B点进发。

等到t2时刻时，蚂蚁2到达了蚁穴A点，蚂蚁1到达了食物所在位置B点，此时蚂蚁2再次出发去搬运食物，它发现AB路径上的信息素浓度要高于AC路径上的信息素浓度（AB路径上有两条虚线，AC路径上只有1条虚线）。因此蚂蚁2选择AB路径去搬运食物，而蚂蚁1则在B点获取到了食物，接下来返回蚁穴，但是它也有两种选择，一种是原路返回，另一种便是走线路AB。蚂蚁1发现AB路径上的信息素浓度要高于BC路径上的信息素浓度，因此它将选择AB来返回蚁穴。

如此往复，AC、BC路径的信息素浓度会越来越低，AB路径上的信息素浓度会越来越高，所以AC路径上将没有蚂蚁再次经过，两只蚂蚁都只会选择路径较短的AB线路去搬运食物。

以上便是蚁群算法的基本原理。

接下来介绍蚁群算法的数学模型，我们以TSP问题为例来进行说明。

TSP（Traveling Salesman Problem）问题，中文叫做旅行商问题：什么是TSP问题，也许有些人还不太清楚。这里做个简要的介绍。TSP问题及著名的旅行商问题，记得第一次接触这个问题是在本科时学习运筹学课程时碰到的一个问题，因此，这个问题是运筹学领域或也可以说是数学领域中的一个著名的问题。这个问题简单描述就是：假设一个旅行商人，他要遍历n个城市，但是每个城市只能遍历一次，最终还要回到最初所在的城市，要求制定一个遍历方案，使经过的总路程最短。

接下来便用蚁群算法对这个问题进行求解：

首先列出一些蚁群算法中涉及到的参数及其符号：

：蚂蚁数量，约为城市数量的1.5倍。如果蚂蚁数量过大，则每条路径上的信息素浓度趋于平均，正反馈作用减弱，从而导致收敛速度减慢；如果过小，则可能导致一些从未搜索过的路径信息素浓度减小为0，导致过早收敛，解的全局最优性降低

：信息素因子，反映了蚂蚁运动过程中积累的信息量在指导蚁群搜索中的相对重要程度，取值范围通常在[1, 4]之间。如果信息素因子值设置过大，则容易使随机搜索性减弱；其值过小容易过早陷入局部最优

：启发函数因子，反映了启发式信息在指导蚁群搜索中的相对重要程度，取值范围在[3, 4.5]之间。如果值设置过大，虽然收敛速度加快，但是易陷入局部最优；其值过小，蚁群易陷入纯粹的随机搜索，很难找到最优解

：信息素挥发因子，反映了信息素的消失水平，相反的反映了信息素的保持水平，取值范围通常在[0.2, 0.5]之间。当取值过大时，容易影响随机性和全局最优性；反之，收敛速度降低

：信息素常数，表示蚂蚁遍历一次所有城市所释放的信息素总量。越大则收敛速度越快，但是容易陷入局部最优；反之会影响收敛速度

：城市数量

：城市i到城市j之间的距离

：t时刻，城市i与城市j之间的信息素浓度

：t时刻，蚂蚁k从城市i向城市j转移的概率

：启发函数，表示蚂蚁从城市i转移到城市j的期望程度，这里我们取值为

：蚂蚁k待访城市的集合，初始时刻中有个元素，即排除掉蚂蚁一开始所在城市以外的其他城市，随着时间推移，其中的城市越来越少，直到为空，表示遍历完所有的城市

：表示在所有蚂蚁遍历完所有城市时，第k只蚂蚁对城市i与城市j之间信息素浓度总增加量的贡献量

：表示所有蚂蚁遍历完所有城市时，城市i与城市j之间信息素浓度的累积增加量

：表示蚂蚁k遍历完所有城市后经历的总路程长度

接下来给出三个公式：

公式一：

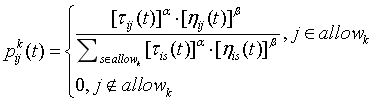
从公式中可以看出信息素因子为信息素浓度的指数，启发函数因子为启发函数的指数，这样便很好理解这两个参数所起到的作用了，分别决定了信息素浓度以及转移期望对于蚂蚁k从城市i转移到城市j的可能性的贡献程度。

公式二：

这个公式反映了信息素浓度的迭代更新规律，可以看出，所有蚂蚁遍历完一次所有城市后，当前信息素浓度由两部分组成，第一部分即上次所有蚂蚁遍历完所有城市后路径上信息素的残留，第二部分为本次所有蚂蚁遍历完所有城市后每条路径上的信息素的新增量。

公式三：

公式三反映了每只蚂蚁对于自己经过的城市之间路径上信息素浓度的贡献量，可以看出，其经历的路程越长，则对于沿途上信息素浓度的贡献量也就越低，如果经历的路程越短，则对于沿途上信息素浓度的贡献量也就越高，结合公式二可以看出，信息素浓度累积贡献量大的路径被选择的概率也就大，这就是为什么能够选出最短路径的原因。关于的计算还有一些其他模型，这里就不详细介绍了，我们这里给出的是ant cycle system模型，也是TSP问题中常用的一种模型。

最后给出蚁群算法解决TSP问题的流程：

组合参数设计策略：

由于蚁群算法对于参数的敏感程度较高，参数设置的好，算法的结果也就好，参数设置的不好则运行结果也就不好。

以上便是蚁群算法的基本原理，以下附上本人用python编写的关于蚁群算法的程序（程序中的参数需要根据具体问题自己进行调整）：

import os
import numpy as np
from numpy import random as rd
import matplotlib.pyplot as plt
np.set_printoptions(linewidth=1000, suppress=True)
# 在D盘根目录放置存放城市间距离矩阵的.txt文件distance.txt，或者存放城市坐标的.txt文件coordinate.txt，城市坐标排成一行，每个坐标用(x,y)表示。
###########distance.txt内容示例##################
"""
0 80 31 83 82 54 100 53 
80 0 58 82 26 35 10 20 
31 58 0 52 82 86 90 75 
83 82 52 0 14 29 41 34 
82 26 82 14 0 60 28 51 
54 35 86 29 60 0 44 66 
100 10 90 41 28 44 0 8 
53 20 75 34 51 66 8 0 
"""
# 如果为n行n列，则说明有n个城市，从第一行到最后一行分别代表城市0到城市n-1，第一列到最后一列也分别代表城市0到城市n-1
# 其中每个元素代表两个城市间的距离，对角线为0是因为自己到自己的距离为0
#############################################
# txt文件中同一行的每个数据之间用空格间隔
# 如果在D盘下两个文件均存在，则只读取distance.txt中的内容
# 根据具体问题复杂程度需要具体调整蚁群算法中的相关参数
os.chdir('D:')
 
 
class ACA(object):
 
    def __init__(self, m, pher_0, alpha, beta, rho, Q, iter_times):
        '''
        :param Q: 信息素常数，表示每只蚂蚁循环一次释放的信息素总量，因此如果选择的路径长度长的话，则路径上信息素浓度Q/L就低
        :param m: 蚂蚁数量，应该大约是城市数量的1.5被
        :param pher_0: 每条路径上的初始时刻信息素浓度
        :param alpha: 信息素因子
        :param beta: 启发函数因子
        :param rho: 信息素挥发程度，取值在0到1之间
        :param iter_times: 算法的迭代次数（外层循环次数，所有蚂蚁遍历完一次所有城市为一次外层循环，所有蚂蚁每遍历一个城市为一次内层循环）
        '''
        self.iter_times = iter_times
        self.Q = Q
        self.rho = rho
        self.alpha = alpha
        self.beta = beta
        self.m = m
        # self.distance_mat为城市间距离矩阵
        if os.path.exists("./distance.txt"):
            self.distance_mat = np.loadtxt(fname="./distance.txt").astype(np.float64)
        elif os.path.exists("./coordinate.txt"):
            self.city_coordinate = [eval(i) for i in np.loadtxt(fname="./coordinate.txt", dtype=np.object)]
            print("城市坐标（0号城市~%d号城市）" % (len(self.city_coordinate) - 1), self.city_coordinate)
            self.distance_mat = self.calc_distance(self.city_coordinate)
        else:
            raise Exception("请按照指定方式命名txt文件名，如果是城市间距离矩阵以distance.txt命名，如果是城市坐标则以coordinate.txt命名")
        print("城市间距离矩阵：\n", self.distance_mat)
        assert np.all(np.logical_not(np.array([self.distance_mat[i, i]
                for i in range(self.distance_mat.shape[0])], dtype=np.bool))), "距离矩阵有误，对角线元素应该为0"
        # self.pher_mat表示城市间信息素浓度矩阵，初始时刻各个城市间信息素浓度均为pher_0
        self.pher_mat = np.array([[pher_0] * self.distance_mat.shape[0]] * self.distance_mat.shape[0])
        # 随机放置蚂蚁初始位
        self.ant_init_position = rd.randint(0, self.distance_mat.shape[0], self.m)
        # 启发函数
        self.heu_f = 1 / (self.distance_mat + np.eye(self.distance_mat.shape[0], dtype=np.float64))
        # self.best_lenth以及self.best_path用来存放每一次迭代最优路径长度以及最优路径
        self.best_lenth = []
        self.best_path = []
 
    def run(self):
        for i in range(self.iter_times):
            # passed_city用来记录每只蚂蚁当前时刻已经路过的城市
            passed_city = [[city] for city in self.ant_init_position]
            for i in range(self.distance_mat.shape[0] - 1):
                # 一次内循环代表所有蚂蚁遍历了一个城市，排除自己初始化时所在城市，每只蚂蚁应该遍历self.distance_mat.shape[0] - 1个城市，
                # 因此内循环应该循环self.distance_mat.shape[0] - 1次
                for passed_ct in passed_city:
                    # 用循环变量passed_ct依次遍历每一只蚂蚁已经路过的城市, 每次遍历出的是一个列表
                    # allow_city为当前蚂蚁还没有遍历到的城市
                    allow_city = list(set(range(self.distance_mat.shape[0])) - set(passed_ct))
                    if len(allow_city) == 1:
                        passed_ct.extend(allow_city)
                        continue
                    # 每只遍历到的蚂蚁从其还没有遍历过的城市allow_city中选择下一个城市select_city,选择依据为概率p_i_j，
                    # 建立一个列表p，表示当前蚂蚁在当前城市到allow_city中每一个城市的概率
                    p = []
                    for allow_ct in allow_city:
                        p_dividend = self.pher_mat[passed_ct[-1], allow_ct] ** self.alpha * self.heu_f[passed_ct[-1], allow_ct] ** self.beta
                        p_divisor = 0
                        for allow_ct_inner in allow_city:
                            p_divisor += self.pher_mat[passed_ct[-1], allow_ct_inner] ** self.alpha * self.heu_f[passed_ct[-1], allow_ct_inner] ** self.beta
                        p_ = p_dividend / p_divisor
                        p.append(p_)
                    select_city_index = p.index(max(p))
                    # 将当前蚂蚁选择出的下一个遍历的城市select_city添加到当前蚂蚁已遍历的城市passed_ct中
                    select_city = allow_city[select_city_index]
                    passed_ct.append(select_city)
            # 更新信息素浓度
            delta_pher_k = []
            delta_pher_mat = np.zeros(self.distance_mat.shape)
            for ant_passed_city in passed_city:
                accumulate_lenth = self.calc_passed_lenth(ant_passed_city)
                delta_pher_k.append(self.Q / accumulate_lenth)
            for i in range(self.m):
                for k in range(self.distance_mat.shape[0] - 1):
                    delta_pher_mat[passed_city[i][k], passed_city[i][k + 1]] += delta_pher_k[i]
                delta_pher_mat[passed_city[i][-1], passed_city[i][0]] += delta_pher_k[i]
            self.pher_mat = (1 - self.rho) * self.pher_mat + delta_pher_mat
            # 所有蚂蚁遍历过一遍所有城市后再次初始化所有蚂蚁的所在城市
            self.ant_init_position = rd.randint(0, self.distance_mat.shape[0], self.m)
            ant_count_passed_path = []
            for i in range(self.m):
                ant_count_passed_path.append(passed_city.count(passed_city[i]))
            best_path_index = ant_count_passed_path.index(max(ant_count_passed_path))
            self.best_path.append(passed_city[best_path_index])
            self.best_lenth.append(self.calc_passed_lenth(passed_city[best_path_index]))
        print("最短路径为(城市编号)：", self.best_path[-1] + self.best_path[-1][:1])
        print("最短路径长度为：", self.best_lenth[-1])
 
    def calc_passed_lenth(self, passed_city):
        lenth = 0
        for i in range(len(passed_city) - 1):
            lenth += self.distance_mat[passed_city[i], passed_city[i + 1]]
        lenth += self.distance_mat[passed_city[-1], passed_city[0]]
        return lenth
 
    def calc_distance(self, city_coordinate):
        """
        :param city_coordinate_mat: 城市坐标
        :return:
        """
        distance = [np.sqrt(np.sum((np.array(i) - np.array(j)) ** 2)) for i in city_coordinate for j in city_coordinate]
        distance = np.array(distance).reshape(len(city_coordinate), len(city_coordinate))
        return distance
 
    def draw(self):
        fig = plt.figure()
        ax = plt.subplot(1, 1, 1)
        ax.plot(np.arange(self.iter_times), self.best_lenth, "*-", color="r", label="best lenth of path every iteration")
        ax.set_xlabel("iteration times")
        ax.set_ylabel("lenth")
        ax.legend()
        plt.show()
        try:
            len(self.city_coordinate)
        except Exception as e:
            pass
        else:
            fig = plt.figure()
            ax = plt.subplot(1, 1, 1)
            x = [self.city_coordinate[i][0] for i in self.best_path[-1] + self.best_path[-1][:1]]
            y = [self.city_coordinate[i][1] for i in self.best_path[-1] + self.best_path[-1][:1]]
            ax.plot(x, y, "o--", color="r", label="route", linewidth=2.5)
            count = 0
            for x_, y_ in zip(x, y):
                count += 1
                if count == len(x):
                    break
                plt.text(x_, y_, "%d(city_%d)" % (count, self.best_path[-1][count - 1]), fontsize=10)
            ax.set_xlabel("x")
            ax.set_ylabel("y")
            ax.set_title("The order of traversing the city")
            ax.legend()
            ax.grid()
            plt.show()
 
 
def main():
    aca = ACA(12, 6, 4.5, 3, 0.6, 500, 2000)
    aca.run()
    aca.draw()
 
 
if __name__ == "__main__":
    main()