数据结构基础和算法图解(2)——线性表_数据结构 线性表locateelem

2. 线性表

2.1 线性表的逻辑结构

1. 线性结构
   线性结构的基本特征为：一个数据元素的有序（次序）集
2. 线性表的抽象数据类型
   线性表是一种最简单的线性结构，线性表的抽象数据类型定义如下：

ADT List{
数据对象：
D={ai|ai∈ElemSet,i=1,2,...n，n>=0}
称n为线性表的表长，称n=0时的线性表为空表
数据关系：
R1={<ai-1,ai>|ai-1,ai∈D，i=2,...,n}
{ 设线性表为（a1,a2,...,ai,....,an}称i为ai在线性表中的位序}
本操作：
结构初始化操作
结构销毁操作
引用型操作
销毁操作
}ADT；
1
2
3
4
5
6
7
8
9
10
11
12
13

3. 线性表的基本操作

(1)结构初始化操作
InitList（&L）
（2）结构销毁操作
DestroyList(&L)
（3）引用型操作
ListEmpty（L） （线性表判空）
ListLength（L） （求线性表的长度）
PriorElem（L，cur_e,&pre_e)(求数据元素的前驱)
NextElem(L,cur_e,&next_e)（求数据元素的后继）
GetElem(L,i,&e)（求线性表某个数据元素，返回线性表中第i个元素的值）
LocateElem(L,e,compare()) （定位函数，返回L中第一个与e相等的位序）
ListTraverse(L,visit())（遍历线性表，初始条件是线性表L存在）
（4）结构初始化操作
ClearList（&L）（线性表置空）
PutElem（&L，i，e）（将e的值赋给第i个元素）
ListInsert（&L，i，e）（插入数据元素，在第i个元素前插入新的元素e，L的长度增1）
ListDelete（&L，i,&e)（删除L的第i个元素，并用e返回其值，L的长度减1）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2.1.1 例题

1. 选修同一门课的学生是线性结构（√）
2. 农贸市场的人群是线性结构（x）
3. 将线性表置为空表，就是销毁这个线性表（x）
4. 线性表的长度必然大于零（X）
5. 线性表中的每个元素，既有前驱，又有后继（X)

2.2 线性表的操作

2.2.1 合并集合

假设有两个集合A和B分别用两个线性表LA和LB表示，即线性表中的数据元素即为集合中的成员，现在求
一个新的集合，要求
A=A∪B
A={1,2,4,6,7}
B={1,3,9,8}

操作步骤：

1. 从线性表LB中依次查看每个数据元素
2. 依值在线性表LA中进行查访
3. 若不存在，则插入之

⭐️ 合并两个数组

void union(List &la,List lb){
	la_len=listlength(la);
	lb_len=listlength(lb);
	for(i=1;i<lb_len;i++){
		GetElem(lb,i,e);
		if(!LocateElem(la,e,equal()))
		   ListInsert(la,++la_len,e);
	}
}
1
2
3
4
5
6
7
8
9

2.2.2 过滤集合中的重复元素

已知一个非纯集合B，试构造一个纯集合A，使A 中只包含B中所有各不相同的数据元素
初始：A={ }，B={6,2,9,3,6}
结果： A={6,2,9,3}
上述问题可以演绎为：
将存在于集合B中的元素逐个放入空集合A中，但A中不能有重复元素，算法策略与例1相同。

⭐️ 过滤集合中的重复元素

void union(List&la,list lb){
	InitList(la);
	la_len=ListLength(la);
	lb_len=listlength(lb);
	for(i=1;i<=lb_len;i++){
		GetElem(lb,i,e);
		if(!LocateElem(la,e,equal()))
			ListInsert(la,++la_len,e);
	}
}
1
2
3
4
5
6
7
8
9
10

2.2.3合并有序表

有序表
若线性表中的数据元素相互之间可以比较，并且数据元素在线性表中依值非递减或者非递增有序排列，
则称改线性表为有序表（Ordered List）
A={1,4,5,7,9,12,15,17,20}
B={2,3,6,6,8}
C=A∪B={1,2,3,4,5,6,6,7,8,9,12,151,7,20}

⭐️ 合并两个有序数组

void MergeList(List la,List lb,List&lc){
	//本算法将非递减的有序表la和lb归并为lc
	InitList(LC);//构造空的线性表lc
	i=j=1;
	k=0;
	la_len=listlength(la);
	lb_le=listlength(lb);
	while((i<=la_len)&&(j<=lb_len)){//la和lb均不为空
		//la和lb均不为空
		GetElem(la,i,ai);
		GetElem(lb,j,bj);
		if(ai<=bj){
			ListInsert(lc,++k,ai);//将ai插入到lc中
			++i;
		}
		eles{
			ListInsert(lc,++k,bj);//将bj插入到lc中
			++j;
		}
	}
	while(i<=la_len){//当la不为空时
		GetElem(la,i++,ai);
		ListInsert(lc,++k,ai);
	}//插入la表中的剩余元素
	while(j<=lb_len){//当lb不为空时
		GetElem(lb,++j,bj);
		ListInsert(lc,++k,bj);
	}//插入lb表中的剩余元素
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

2.3 顺序表

2.3.1线性表的顺序存储结构

length: 当前元素个数（当前已经占用的存储空间的大小）
listsize: 当前分配的存储空间大小
ElemType *elem : 指向存储空间的基地址

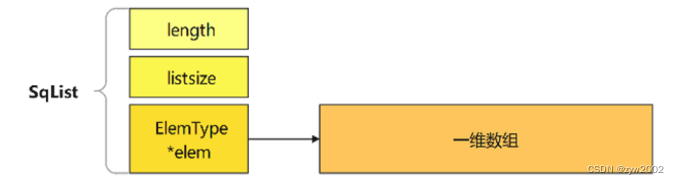
2.3.1.1 顺序表初始化

#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
typedef struct{
	ElemType *elem; //存储空间基址
	int length;//当前长度
	int listsize;//当前分配的存储容量
}SqList; //称为 顺序表
//顺序表的初始化
Status InitList_Sq(SqList& L){
	L.elem=(ElemType*)malloc(LIST_init_SIZE*sizeof(ElemType));
	if(!L.elem)exit(OVERFLOW);
	L.length=0;
	L.listsize=LIST_INIT_SIZE;
	return OK;
}//Init_Sq
//算法时间复杂度O（1）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

2.3.2 顺序表的查找

int LocateElem_Sq(SqList L,ElemType e,Status (*compare)(ElemType,ElemType)){
	//在顺序表中查询第一个满足判定条件的数据元素
	//若存在，则返回它的位序，否则返回0
	i=1; //i 的初值为第1元素的位序
	p=L.elem;
	while(i<=L.length&&!(*compare)(*p++,e))
		++i;
	if(i<=L.length)
		return i;
	else 
		return 0;
}//LocateElem_Sq
//算法时间复杂度O（ListLength(L)
1
2
3
4
5
6
7
8
9
10
11
12
13

2.3.1.3 例题

1. 编程时如何定义顺序表

typedef struct{
	int *elem;//存储空间基址
	int length;//当前长度
	int listsize; //当前分配的存储容量，以sizeof(ElemType)为单位
}SqList; //称为顺序表
1
2
3
4
5

2. malloc函数如何使用

L.elem=(int*)malloc(LIST_INIT_SIZE*sizeof(int));
1

3. 如何引用顺序表中的变量

// 第一个元素a0: L->elem[0]
//第i个元素ai: L->elem[i-1]
//第n个元素an： L->elem[n-1] 或者L->elem[L->length-1]
1
2
3

2.3.2 顺序表的插入

Status LisInsert_Sq(SqList&L,int i,ElemType e){
	if(i<1||i>L.length+1)
		return ERROR; //插入位置不合法
	if(L.length>=L.listsize){//分配存储空间
		newbase=(ElemType *)realloc(L.elem,
		(L.listsize+LISTINCREMENT)*sizeof(ElemType));
		if(!newbase)
			exit(OVERFLOW);
		L.elem=newbase;
		L.listsize+=LISTINCREMENT;
	}
	q=&(L.elem[i-1]);//q指示插入位置
	for(p=&(L.elem[L.length-1]);p>=q;--p)
		*(p+1)=*p; //插入位置及之后位置向后移位
	*q=e; //插入e
	++L.length; //表长增1
	return OK
}
//时间性能 若在线性表中任何一个位置上进行插入的概率都是相等的，则移动元素的期望值为： n/2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

2.3.2.1例题

1. 长度为n的顺序表，一共有 n+1 个插入位置，在第i个元素前插入一个新的元素，要移动的元素个数是 n-i+1
2. 指针q指向顺序表的第i个元素用c语言程序表示：

q=&（L.elem[i-1]);
1

3. 在顺序表中，指针p所指向的元素后移一位：

*(p+1)=*p;
1

2.3.3 顺序表的删除

Status ListDelete_Sq(SqList &L,int i,ElemType &e){
	if((i<1)||(i>L.length))
		return ERROR;//删除位置不合法
	p=&(L.elem[i-1]);// p为被删除元素的位置
	e=*p; //被删除元素的值赋给e
	q=L.elem+L.length-1; //表尾元素的位置
	for(++p;p<=q;++p)
		*(p-1)=*p;//被删除元素之后的元素左移
	--L.length;//表长减1
return OK
}
//删除算法的时间性能
// E=qi(n-i) 求和（i-1到n）
//若假定在线性表中任何一个位置上进行删除的元素概率相等 则 E=n-1/2
1
2
3
4
5
6
7
8
9
10
11
12
13
14

2.3.3.1 例题

1. 长度为n的顺序表，一共有 n 个删除位置，如果要删除第i个元素，要移动的元素个数是 n-i个
2. 指针q指向顺序表（表长为n）的元素用c语言程序表示

q=&(L.elem[n-1]);
//或
q=L.elem+L.length-1;
1
2
3

3. 在顺序表中，指针p所指向的元素前移一位如何用c语言程序表示：

*(p-1)=*p;
1

2.3 单链表

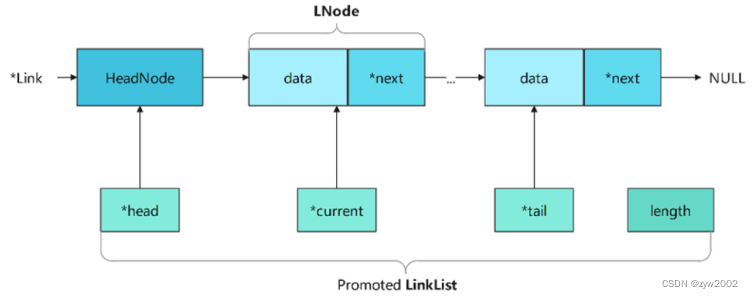
用一组地址任意的存储单元存放线性表中的数据元素
结点和单链表的类C语言描述

Typedef struct LNode{
	ElemType data; //数据域
	struct LNode *next //指针域
}LNode,*LinkList;
LinkList L; //L为单链表的头指针
1
2
3
4
5

2.3.1 生成链表

生成链表的过程是结点逐个插入的过程
⭐️ 头插法生成链表

void CreateList_L(LinkList& L,int n){ 
	//逆序输入n个数据元素，建立带头结点的单链表
	L=(LinkList)malloc(sizeof(LNode));
	L->next=NULL; //先建立一个带头结点的单链表
	for(i=n;i>0;--i){
		p=(LinkList)malloc(sizeof(LNode));
		scanf(&p->data); //输入元素值
		p->next=L->next;
		L->next=p; //插入
	}
}//插入
1
2
3
4
5
6
7
8
9
10
11

2.3.2 获取元素

Status GetElem(LinkList L,int i,ElemType &e){
	p=L->next;
	j=1;
	while(p&&j<i){
		p=p->next;
		++j;
	}
	if(!p||j>i)
		return ERROR;//第i个元素不存在
	e=p->data; //取得第i个元素
	return OK;
}
//算法时间复杂度 O（n） n为单链表的长度
1
2
3
4
5
6
7
8
9
10
11
12
13

2.3.3 单链表存储结构改进

typedef struct LNode{
	ElemType data;
	struct LNode *next;
}*Link,*Position;
typedef struct{
	Link head,tail;//分别指向头结点和最后一个结点的指针
	int len;//指示链表长度
	Link current;//指向当前被访问的结点的指针，初始位置指向头结点
}LinkList;
1
2
3
4
5
6
7
8
9

2.3.4 例题

1. L是单链表的头指针，L指向头结点，单链表的第一个元素如何指向
   L->next;
2. 指针p指向单链表中的第i个元素ai，ai+2如何指向？
   p->next->next;
3. 欲在单链表的尾部增加一个新结点，必须遍历整个链表？
   要看单链表的结构而定

2.3.5 单链表的插入

1. 找到线性表中第i-1个结点
2. 修改其指向后继的指针

Status ListInsert_L(LinkList L,int i,ElemType e){
	//本算法在链表中第i个结点之前插入新的元素e
	p=L;
	j=0;
	while(p&&j<i-1){
		p=p->next;
		++j; //寻找第i-1个结点
	}
	if(!p||j>i-1)
		return ERROR; //i大于表长或者小于1
	S=(LinkList)malloc(sizeof(LNode)); //生成新结点
	s->data=e;
	s->next=p->next;
	p->next=s; //插入
}
//算法时间复杂度 O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

2.3.5.1 例题

1. 指针p指向单链表的第i个元素ai，欲在ai后面连续插入两个元素m和n，写出主要算法

s=(LinkList)malloc(sizeof(LNode));
s->data=m;
s->next=p->next;
p->next=s;
p=s;
s=(LinkList)malloc(sizeof(LNode));
s->data=n;
s->next=p->next;
p->next=s;
1
2
3
4
5
6
7
8
9

2.3.6 单链表的删除

// 将链表第i个元素删除
Status ListDelte(LinkList L,int i,Elmetype &e){
	p=L; j=0;
	while(p->next&&j<i-1){
		p=p->next;
		++j;
	}
	if(!(p->next)||j>i-1)
		return ERROR;
	q=p->next;
	p->next=q->next;
	e=q->data;
	free(q);
	return OK;
}

//清空链表
void ClearList(&L){
	while(L->next){
		p=L->next;
		L->next=p->next;
		free(p);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

例题

1. 连续删除两个元素

q=p->next;
p->next=q->next;
free(q);
q=p->next;
p->next=q->next;
free(q);
1
2
3
4
5
6

2.4 单循环链表

最后一个结点的指针域的指针又指回头结点的链表
判别链表最后一个结点的条件是： 后继结点是否指向头结点

Typedef struct LNode{
	ElemType data; //数据域
	struct LNode *next //指针域
}LNode,*LinkList;

void CreatList(LinkList L,int n){
	int i;
	Lnode *p,*s;
	p=L;
	for(i=1;i<n;i++){
		s=(LinkList)malloc(sizeof(LNode));
		s->data=i+1;
		s->next=p->next;
		p->next=s;
		p=s;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2.5 双向链表

typedef struct DuLNode{
	ElemType data; //数据域
	struct DuLNode *prior; //指向前驱的指针域
	struct DuLNode *next; //指向后继的指针域
}DuLNode, *DuLinkList;
void CreatListHead(DuLinkList L,int n){
	int i;
	LNode *p,*s;
	p=L;
	for(int i=0;i<n;i++){
		printf("请输入第%d个元素：",i+1);
		s=(DuLinkList)malloc(sizeof(LNode));
		scanf("%d",&s->data);
		s->next=p->next;
		s->prior=p;
		p->next=s;
		if(s->next)
			s->next->prior=s;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

2.5.1 双向链表的插入

s->next=p->next;
p-next=s;
s->next->prior=s;
s->prior=p;
1
2
3
4

2.5.2例题

在双向链表中的元素ai前插入一个新元素e，指针p指向结点ai，写出相应的算法语句

s=(DuLinkList)malloc(sizeof(DulNode));
s->data=e;
s->prior=p->prior;
p->prior->next=s;
s->next=p;
p->prior=s;
1
2
3
4
5
6

2.5.3双向链表的删除

q =p->next
p->next=p->next->next;
q->next->prior=p;
free(q);
1
2
3
4

2.5.3.1 例题

1. 删除双向链表中的元素ai，指针p指向结点ai，写出相应的算法语句

e=p->data;
p->prior->next=p->next;
p->next->prior=p->prior;
free(p);
1
2
3
4

2.6.1例题

2.6.1.1单循环列表的转置

Status Contrary(LinkList &L){
	t=L; //t指向单循环链表的头结点
	p=t->next; //p指向单循环链表的第一个结点
	q=p->next; //q指向单循环链表的第二个结点
	while(p!=L){
		p->next=t; //让p结点next域指针指向其前驱
		t=p; //顺链向后移动指针t
		p=q; //顺链向后移动指针p
		q=p->next; //顺链向后移动指针q
	}
	L->next=t; //让L的next域指针指向新链表的第一个结点
	return OK;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

2.6.1.2约瑟夫环

void LinkListDelete(LinkList L,int n,int m)
{//依次删除不带头结点单循环链表的第m个元素
	LNode *p,*s;
	int i,j;
	p=L;
	for(i=0;i<n;i++)
	{
		j=1;
		while(j<m-1)//直到p指向第m-1个元素
		{
			p=p->next;
			j++;
		}
		s=p->next;//s指向第m个元素，删除该结点
		p->next=s->next;
		printf("%d",s->data);
		free(s);
		p=p->next;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20