神奇cpp

这个屌丝很懒，什么也没留下！

热门标签

信号处理基础之噪声与降噪(三) | EMD降噪与VMD降噪及python代码实现_emd和vmd

作者：神奇cpp | 2024-07-04 08:12:09

踩

emd和vmd

1 EMD降噪

1.1 EMD的基本原理

经验模态分解（Empirical Mode Decomposition, EMD）是将复杂信号分解为有限个固有模态函数（Intrinsic Mode Function, IMF）和残差信号的方法，如图1所示。

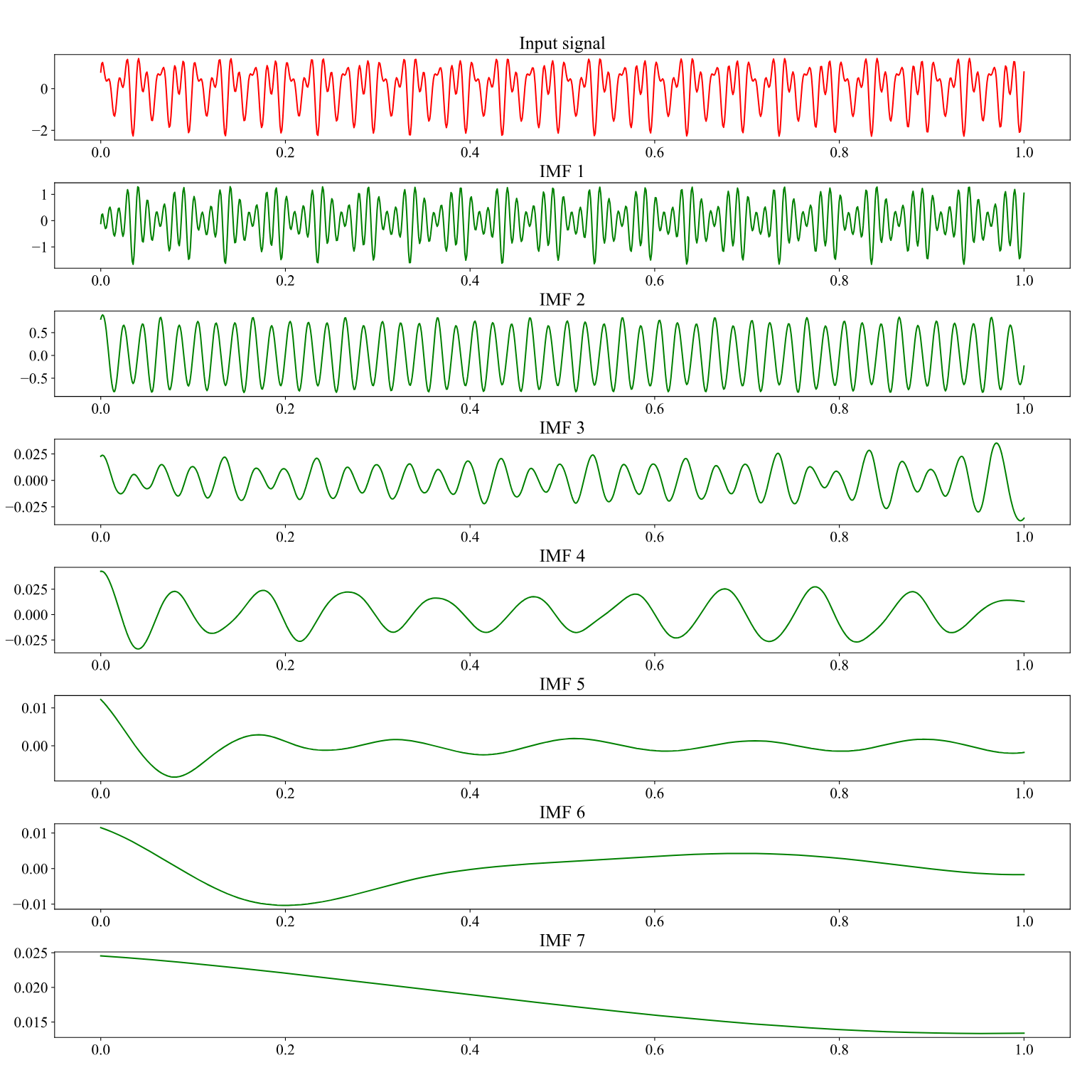
图1 EMD与IMFs

各IMF分量包含了原始信号的不同时间尺度的局部特征信号，IMF信号仅包含一种振荡模式（即单一的瞬时频率），IMF需要满足以下两个条件：

（1）极值点和过零点的数目应相等，或最多相差一个；

（2）局部最大值和局部最小值的上下包络线均值为零。

EMD分解的步骤如下：

（1）包络线获取：确定原始信号 $y(t)$ 的极大值序列 $y_{max}[n]$ 和极小值序列 $y_{min}[n]$ ，采用三次样条曲线对极值点进行拟合，形成上下包络线 $y_{max}(t)$ ， $y_{min}(t)$ ，此处常用希尔伯特变换（Hilbert Transform, HT）求取包络线，计算上下包络线的平均值：

$y_{mean}(t)=\frac{y_{max}(t)+y_{min}(t)}{2}$

（2）残余信号获取：原始信号 $y(t)$ 与平均包络信号 $y_{mean}(t)$ 做差，得到残余信号；

（3）IMF条件检验：检验 $h(t)$ 是否满足IMF条件，当满足时即获得一个固有模态函数 $c_i(t)$ ，若不满足则重复步骤（1）和（2）；

（4）残差信号获取：原始信号 $y(t)$ 与平均包络信号 $c(t)$ 做差，得到残余信号，将残差信号作为原始信号重复以上过程，不断得到各固有模态函数：

$r(t)=y(t)-c(t)$

（5）分解终止标志：当残差信号 $r(t)$ 为单调函数时，终止分解，此时原始信号可表示为：

$y(t)=\sum_{i=1}^{n}c_i(t)+r_n(t)$

1.2 EMD降噪的实现过程

根据EMD分解过程不难看出，在进行信号处理时，只需要对信号分解的IMFs和残差信号进行约束，然后采用分解得到的IMFs对信号重构，即可获得降噪的信号。基于EMD的降噪过程包括以下步骤：

（1）EMD分解：得到一系列IMFs和残差信号；

（2）IMFs筛选：筛选包含有用信息的IMFs；

（3）信号重构：将筛选的IMFs叠加，获得降噪后的信号。

不难发现，基于EMD的降噪过程中，最关键的是IMFs的筛选，目前常用的方法包括频谱筛选法、峭度/峰值因子筛选法、相关系数筛选法和自适应法（该部分暂不进行展开）等。

频谱筛选法：计算各IMF的频谱，根据需要选取频段筛选IMFs，但这种方法基于研究人员清晰知道自己所需的频段；

峭度/峰值因子筛选法：计算各IMF的峭度值或峰值因子，一般认为峭度值越大信号中包含较多的毛刺，该类信号通常与噪声相关，重构时进行去除；

相关系数筛选法：计算IMFs和原始信号的相关系数，设置合理阈值，筛选需要的IMF重构信号。一般地，相关系数介于-1和1之间，相关系数绝对值越大，信号相关性越强。

1.3 EMD的不足

采用EMD分解的方法，一般存在末端效应和模态混叠的问题。

末端效应：发生在信号的头部或者尾部，通常由于拟合包络线时末端发散导致，进而扭曲IMF末端的波形；

模态混叠：在同一个IMF分量中,存在尺度分布范围很宽却又各不相同的信号；在不同的IMF分量中,存在着尺度相近的信号。模态混叠主要是因为：在求取包络线的过程中，信号中存在异常事件，影响极值点的选取，使极值点分布不均匀，从而导致求取的包络为异常事件的局部包络和真实信号包络的组合。经该包络计算出的均值，再筛选出的IMF分量就包含了信号的固有模式和异常事件或者包含了相邻特征时间尺度的固有模式，从而产生了模态混叠现象。

1.4 EMD降噪的python实现


from PyEMD import EMD
import numpy as np
from scipy.stats import kurtosis
 
def denoised_with_EMD(data):
    imf_select = []
    order_select = []
    # EMD分解
    emd = EMD()
    imfs = emd.emd(data)
    for i in range(len(imfs)-1):
        print(kurtosis(imfs[i]))
        if kurtosis(imfs[i]) < 0:
            imf_select.append(imfs[i])
            order_select.append(i+1)
        else:
            continue
    signal_denoised = np.sum(imf_select[:len(imf_select)], axis=0)
    return imf_select, order_select, signal_denoised

2 VMD降噪

2.1 VMD的基本原理

变分模态分解（Variational Mode Decomposition, VMD）假设信号由一系列具有特定中心频率、有限带宽的子信号（IMFs）组成，如图2所示。因此VMD问题最终即是求解中心频率与带宽限制的问题，其在经典wiener滤波的基础上，通过变分问题进行求解，最终得到模态函数。VMD的数学原理和推导过程较为复杂，本文不进行详细展开，具体过程可参考文献[1]。

图2 VMD分解

实际上，变分问题最终是求解泛函的极值问题，最终可以转换成优化求解的问题，VMD过程可简单描述如下：

（1）变分问题构造/优化模型构造

以下从优化模型的角度对变分问题进行简单介绍，假设信号可分解为K个有限带宽的模态分量 $v_k(t)$ 组成，每个IMF中心频率为 $\omega(t)$ ，则优化模型可表示如下：

目标函数：通过希尔伯特变换并采用算子 $e^{-j{\omega_k}t}$ 调制得到基带，计算解调梯度的平方范数，并估计每个模分量的带宽，最终得到如下目标函数：

$min\,\,\,\sum_k|| \partial _t[(\delta(t)+\frac{j}{{\pi}t})v_k(t)]e^{-j{\omega_k}t}||^2$

约束条件：模态和等于输入信号，表示如下：

$s.t.\,\,\,\,\,\,\sum_k{v_k(t)}=y(t)$

设计变量：模态分量 $v_k(t)$ ，每个IMF中心频率为 $\omega(t)$ 。

（2）变分问题求解

以上优化模型的求解可采用诸多优化求解器，包括二次惩罚项、拉格朗日算子、增广拉格朗日函数等，各求解过程较为复杂，此处不展开讨论，感兴趣可参考文献[2]。

在使用VMD分解时，需要设定两个重要参数，即分解层数K和惩罚因子α（优化求解时引入的二阶惩罚系数），两个分解参数对结果影响较大。当分解层数K小于待分解信号的有效成分的个数时，出现欠分解，导致模态混叠，当分解层数K大于待分解信号中的有用成分的个数时，出现过分解，产生虚假分量，为了获取最佳的K值，可使用峭度最大原理、能量差值原则和优化算法进行计算。惩罚系数 α 决定着IMF分量的带宽，惩罚系数越小，各 IMF 分量的带宽越大，过大的带宽会使得某些分量包含其他分量信号；α值越大，各IMF分量的带宽越小，过小的带宽是使得被分解的信号中某些信号丢失，该系数常见取值范围为1000~3000。

2.2 VMD降噪的实现过程

与EMD降噪过程类似，VMD降噪过程如下：

（1）VMD分解：得到各模态分量IMF；

（2）IMFs筛选：筛选包含有用信息的IMFs；

（3）信号重构：将筛选的IMFs叠加，获得降噪后的信号。

2.3 VMD的优点

（1）可自定义模态个数；

（2）通过VMD方法分解出来的IMF都具有独立的中心频率，并且在频域上表现出稀疏性的特征，具备稀疏研究的特质；

（3）在对IMF求解过程中，通过镜像延拓的方式避免了类似EMD分解中出现的端点效应；

（4）通过合理的K值选取可避免模态混叠。

2.4 VMD降噪的python实现


 
import numpy as np
from scipy.stats import kurtosis
from vmdpy import VMD
 
def denoised_with_VMD(data):
    imf_select = []
    order_select = []
    # VMD分解,alpha为惩罚因子，K为分解层数，tol为优化终止条件
    u, u_hat, omega = VMD(data, alpha=2000, tau=0.0, K=4, DC=0, init=1, tol=1e-7)
    for i in range(len(u)):
        if kurtosis(u[i]) < 0:
            imf_select.append(u[i])
            order_select.append(i+1)
        else:
            continue
    signal_denoised = np.sum(imf_select[:len(imf_select)], axis=0)
    return imf_select, order_select, signal_denoised

3 算法测试

3.1 测试用例


import matplotlib.pyplot as plt
import matplotlib
 
n = 500  # 生成500个点的信号
t = np.linspace(0, 30*np.pi, n, endpoint=False)
s = np.cos(0.1*np.pi*t) + np.sin(0.3*np.pi*t) + np.cos(0.5*np.pi*t) + np.sin(0.7*np.pi*t)  # 原始信号
r = 0.5 * np.random.randn(n)  # VMD噪声
# r = 0.1 * np.random.randn(n)  # EMD噪声
y = s + r  # 加噪声
 
imf_select, order_select, signal_denoised = denoised_with_VMD(y)
n = len(imf_select) + 2
fig = plt.figure(figsize=(16, 12))
plt.subplots_adjust(hspace=0.5)
font = {'family': 'Times New Roman', 'size': 16, 'weight': 'normal',}
matplotlib.rc('font', **font)
 
plt.subplot(n, 1, 1)
plt.plot(t, y, linewidth=1.5, color='b')
plt.title('原始模拟信号', fontname='microsoft yahei', fontsize=16)
 
for i in range(2,n):
    plt.subplot(n, 1, i)
    plt.plot(t, imf_select[i-2], linewidth=1.5, color='r')
    plt.title('IMF%d'%order_select[i-2], fontname='microsoft yahei', fontsize=16)
 
plt.subplot(n, 1, n)
plt.plot(t, signal_denoised, linewidth=1.5, color='b')
plt.title('降噪信号', fontname='microsoft yahei', fontsize=16)

3.2 降噪结果

图3为EMD降噪结果，图4为VMD降噪结果。

图3 EMD降噪

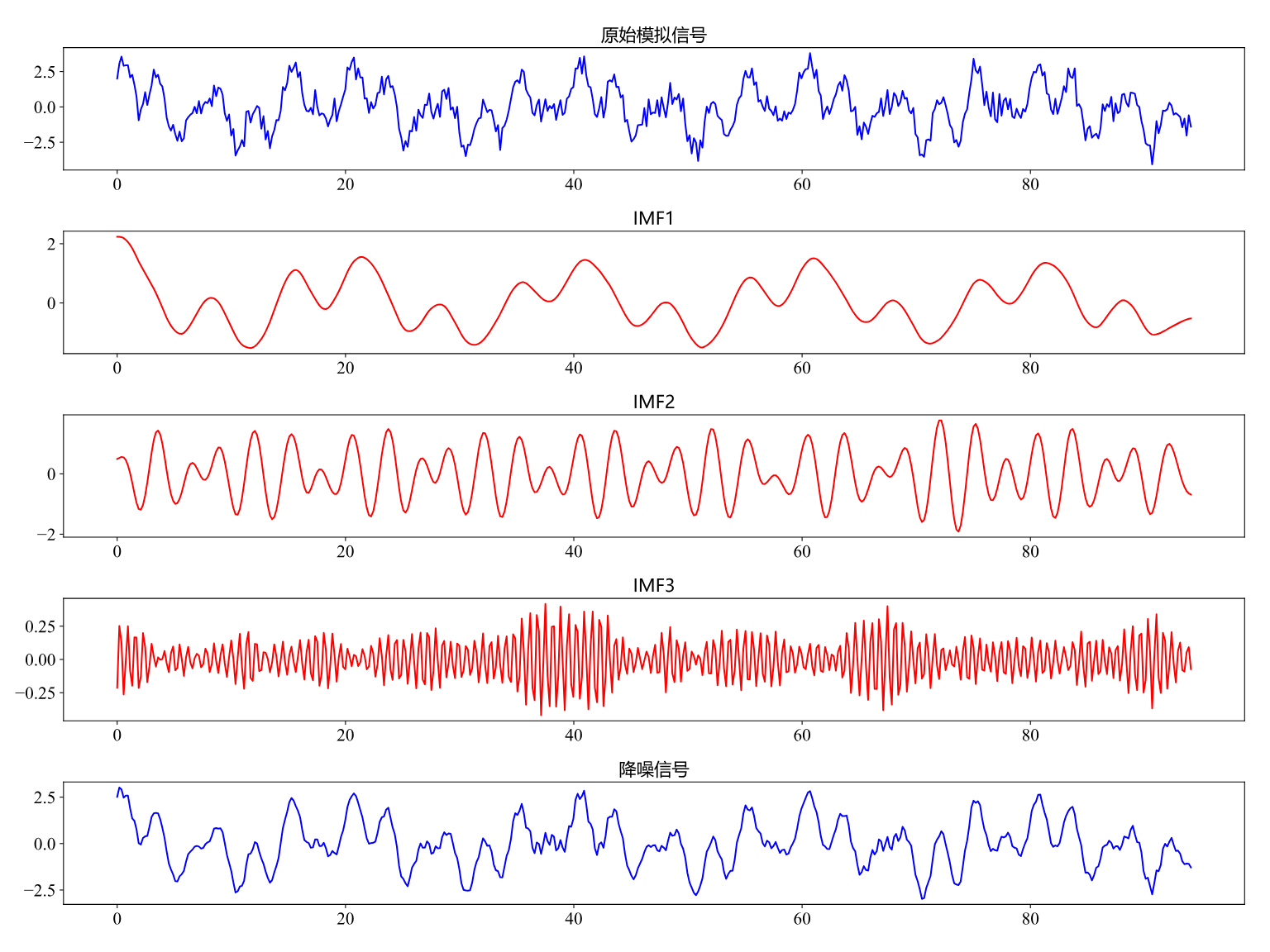
图4 VMD降噪

3.3 降噪指标

4 参考文献

[1]Dominique, Zosso, Konstantin, et al. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing A Publication of the IEEE Signal Processing Society.

[2]蔺梦雄,焦博森,杨琰,等. 基于VMD降噪的RV减速器故障诊断[J]. 北京联合大学学报,2023,37(3):7-13.

[3]https://zhuanlan.zhihu.com/p/608044525?utm_id=0

[4]https://zhuanlan.zhihu.com/p/396775790

更多内容，请关注公众号故障诊断与python学习

本文内容由网友自发贡献，转载请注明出处：https://www.wpsshop.cn/w/神奇cpp/article/detail/786195