- 1第三章:AI大模型的开发环境搭建3.1 Python编程基础3.1.2 Python库与模块_python 大语言模型 开发
- 27.1 数据库设计概述
- 3Visual Studio Code使用问题_若您正以管理员身份运行 visual studio code 用户范围的安装,更新功能会被禁用。
- 4pandas 用read_csv读取txt文件时,部分行丢失_pandas读取txt文件不全
- 5linux相对于windows环境为啥相对来说更加具有安全性_对于普通用户linux和windows哪个安全
- 6Linux权限有哪些?500代表什么意思?_权限500啥意思
- 7Redis主从配置
- 8人工智能火爆了!阿里机器人都会批改作文了!苹果开源机器学习框架;360 开源深度学习平台 XLearning;
- 9【卡车无人机协同】基于遗传算法卡车和两架无人机配送路径规划附matlab代码_卡车支持无人机运行配送
- 10NOIP 边权差值最小的生成树(小数据)_最小边权差生成树
【算法】经典算法题合集_算法大全
赞
踩
专题一:双指针
1. 移动零

题目解析

算法原理
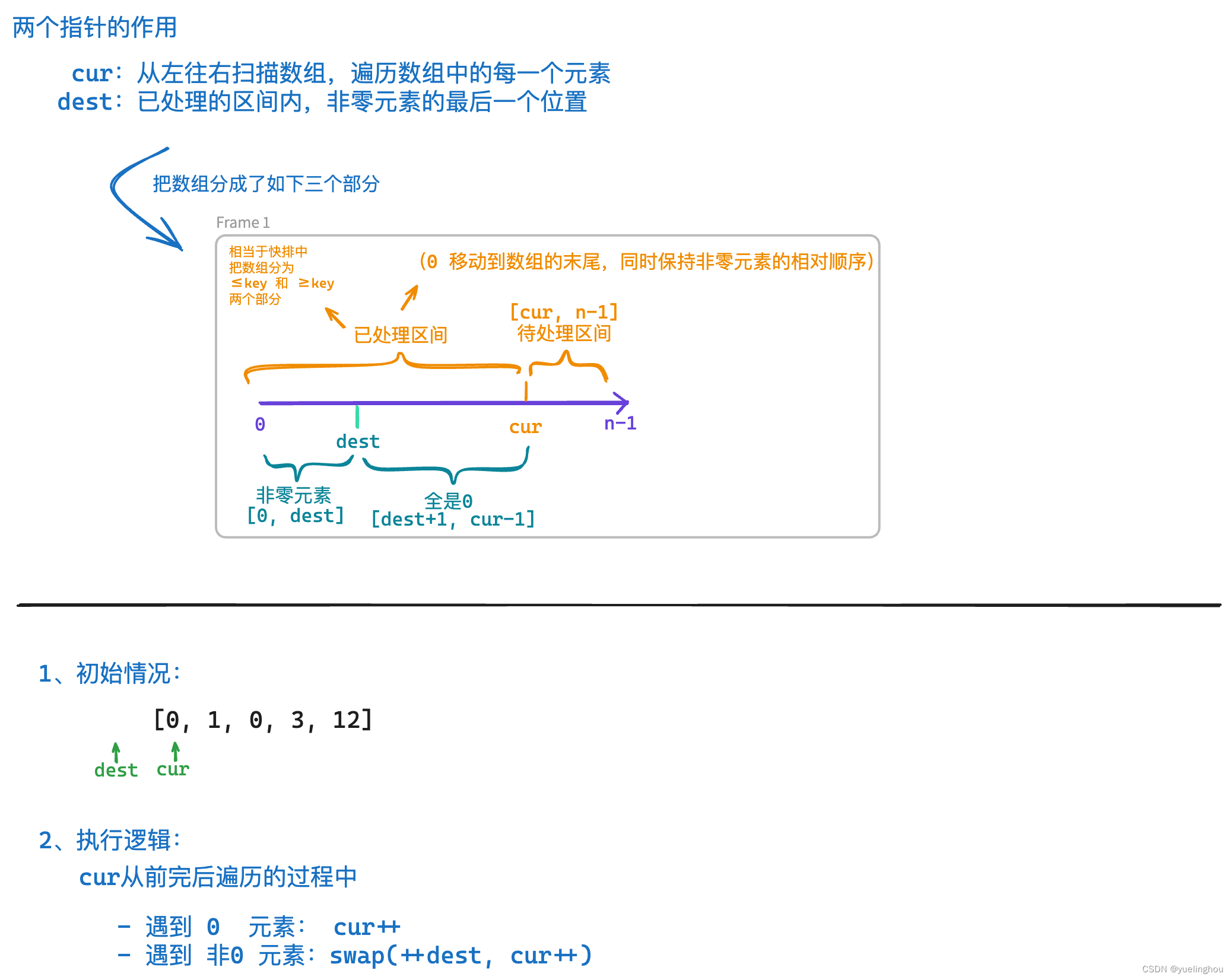
代码编写
// 写法一 class Solution { public: void moveZeroes(vector<int>& nums) { // 1、下标初始化 int dest = -1, cur = 0; // 2、数组划分 while(cur < nums.size()) { if(nums[cur]) swap(nums[++dest], nums[cur++]); else ++cur; } } }; // 写法二 class Solution { public: void moveZeroes(vector<int>& nums) { for(int dest = -1, cur = 0; cur < nums.size(); ++cur) if(nums[cur]) // 处理 非0 元素 swap(nums[++dest], nums[cur]); } }; /* - 时间复杂度:O(n) - 空间复杂度:O(1) */
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
2. 复写零

算法原理
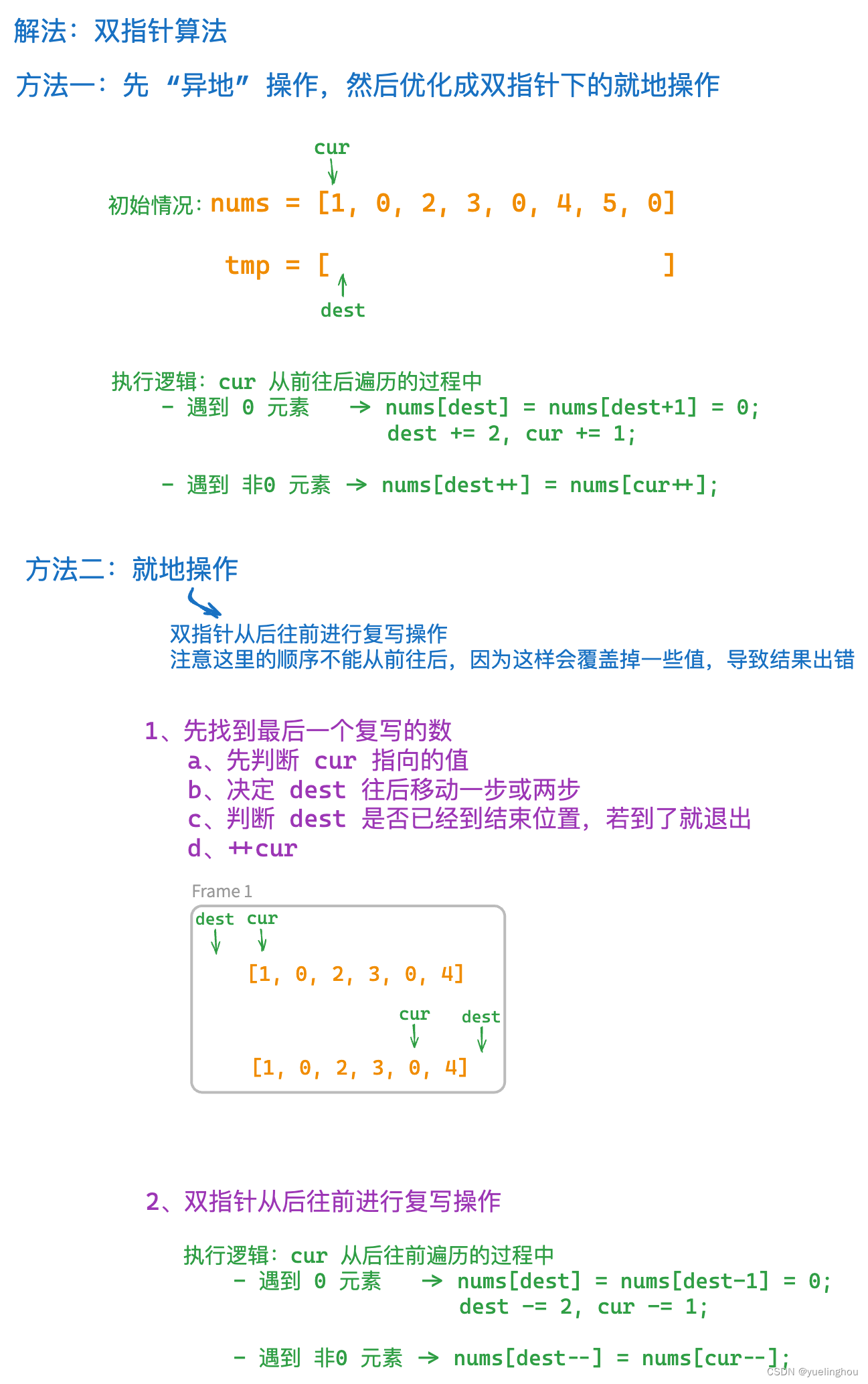
代码编写
class Solution { public: void duplicateZeros(vector<int>& nums) { // 1、初始化 int dest = -1, cur = 0, n = nums.size(); // 2、找到最后一个复写的数 while(true) { if(nums[cur]) dest += 1; else dest += 2; if(dest >= n - 1) break; ++cur; } cout << nums[cur] << endl; // 1.5、预处理 -> 让 dest 的下标有效 if(dest == n) { if(nums[cur]) --cur, --dest; else { nums[n - 1] = 0; dest -= 2; cur -= 1; } } // 2、双指针从后往前进行复写操作 while(cur >= 0) { if(nums[cur]) nums[dest--] = nums[cur--]; else { nums[dest--] = 0; nums[dest--] = 0; cur--; } } } }; /* - 时间复杂度:O(n) - 空间复杂度:O(1) */
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
3. 快乐数
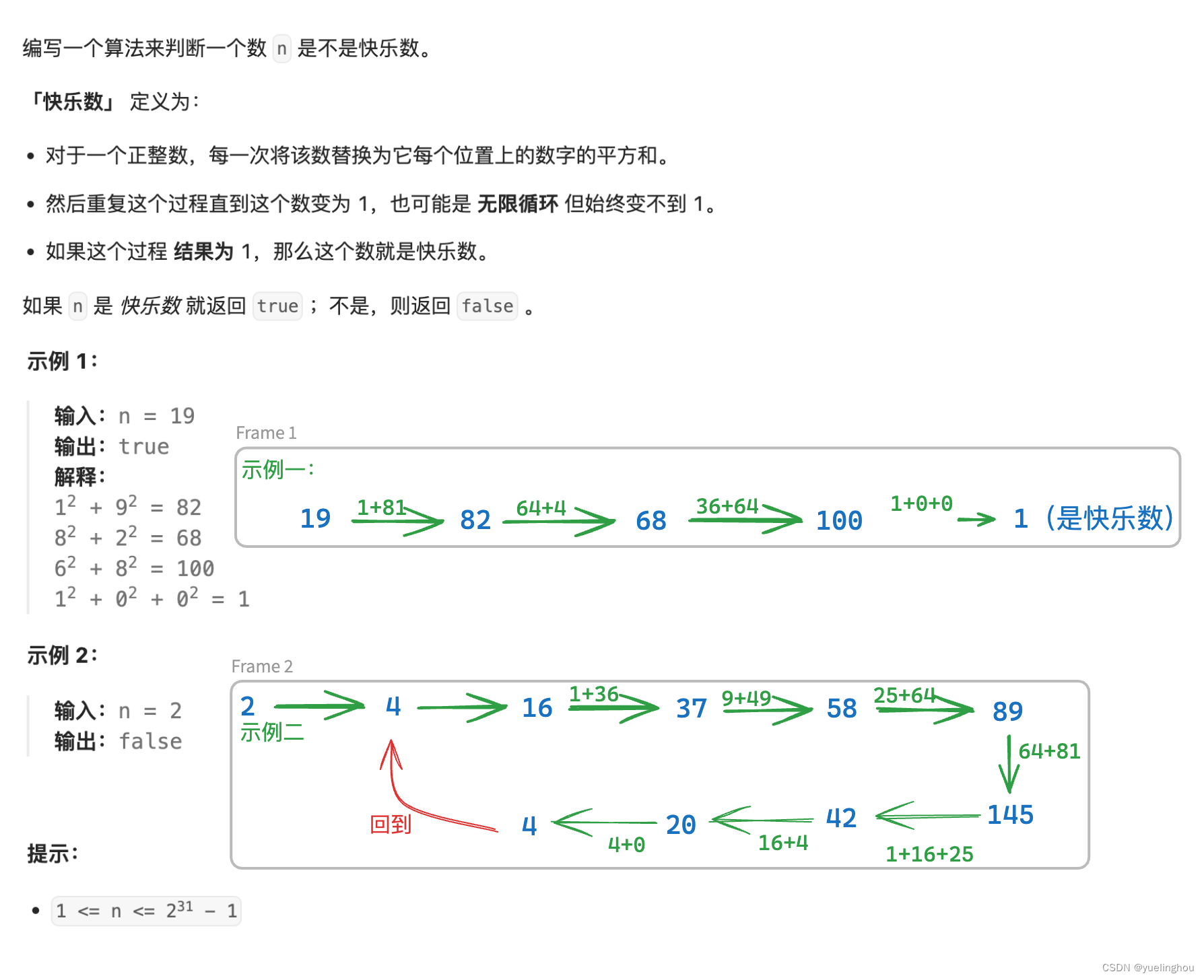
算法原理
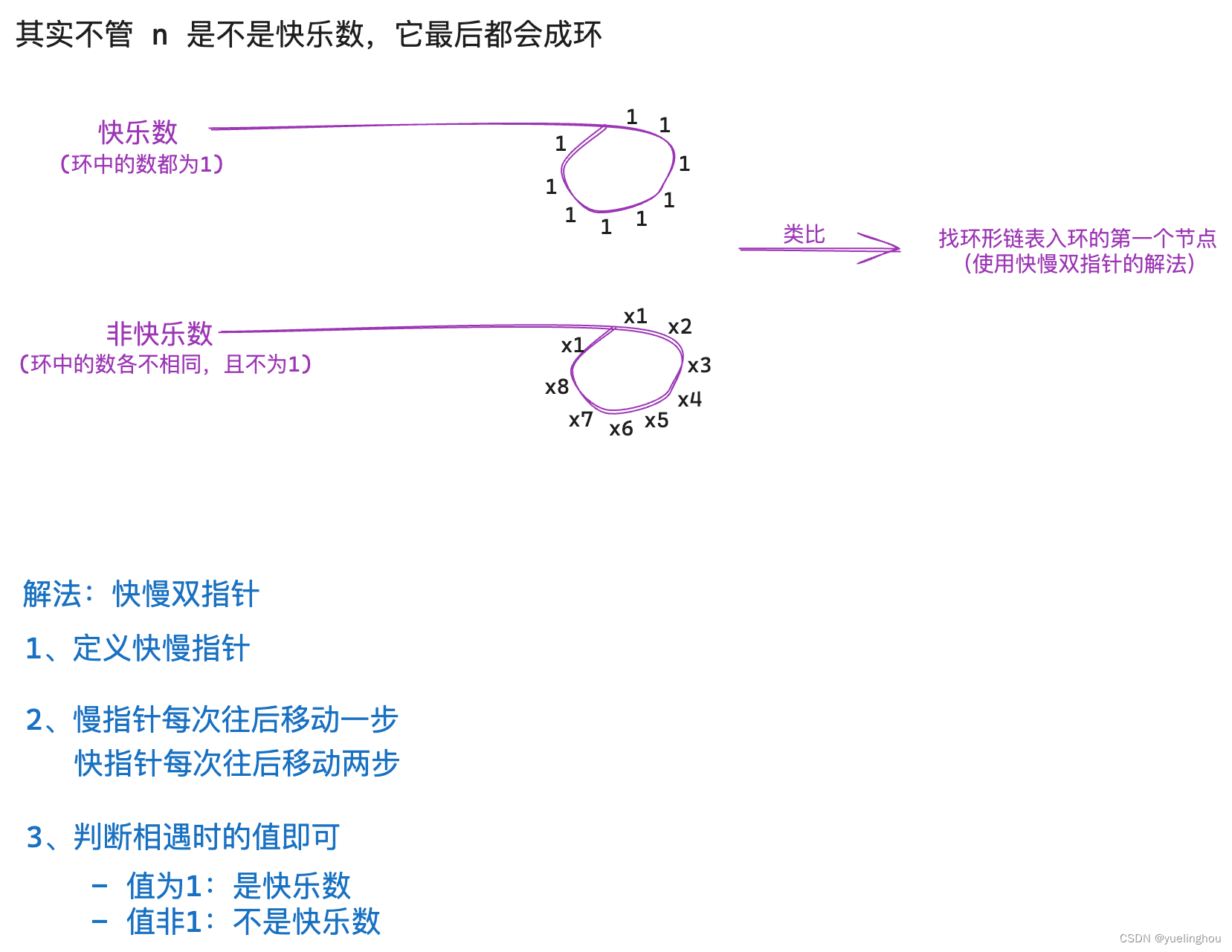
代码编写
class Solution { private: // 计算每个位置上的数字的平方和 inline static int BitSum(int num) { int ret = 0; while(num) { int t = num % 10; ret += t * t; num /= 10; } return ret; } public: bool isHappy(int n) { int slow = n, fast = BitSum(n); while(slow != fast) { slow = BitSum(slow); fast = BitSum(BitSum(fast)); } return slow == 1; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
4. 盛最多水的容器

算法原理
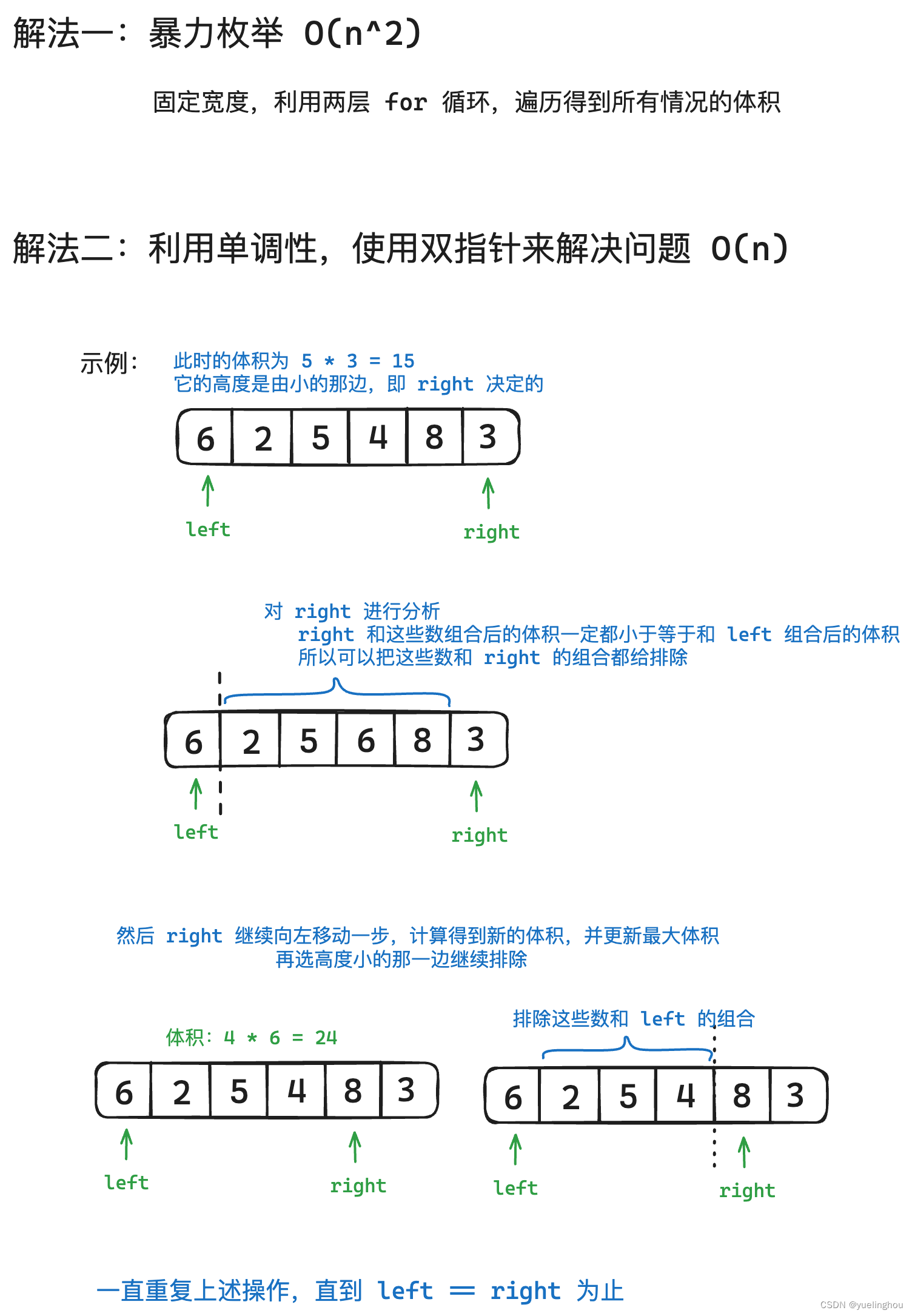
代码编写
class Solution { public: int maxArea(vector<int>& height) { int left = 0, right = height.size() - 1; int ret = INT_MIN; while(left != right) { // 容积 = 长度 * 高度 int v = (right - left) * min(height[left], height[right]); ret = max(ret, v); // 移动指针 - 谁小移动谁 height[left] < height[right] ? ++left : --right; } return ret; } }; /* - 时间复杂度:O(n) - 空间复杂度:O(1) */
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
5. 有效三角形的个数

算法原理
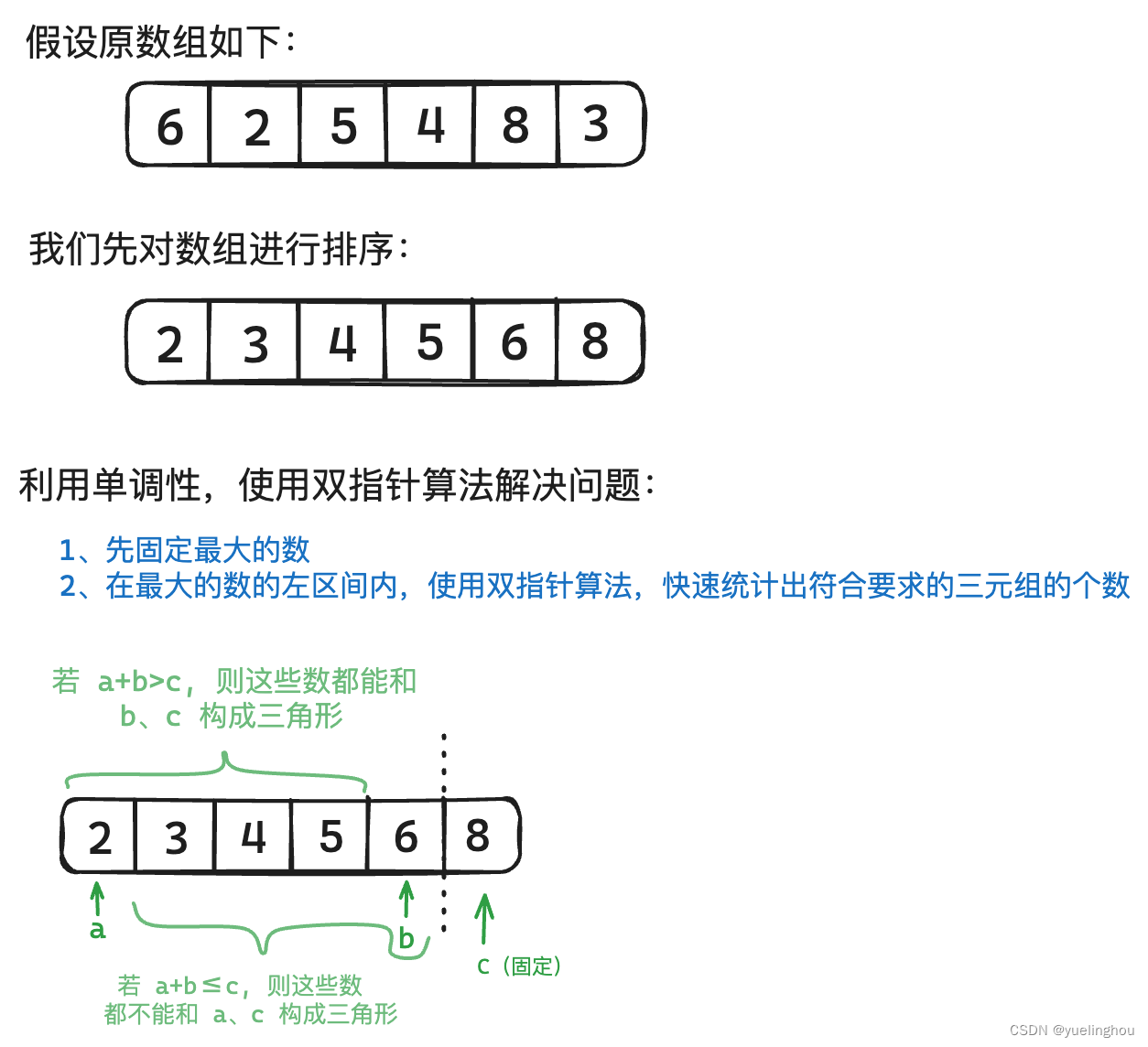
代码编写
class Solution { public: int triangleNumber(vector<int>& nums) { // 1、优化 sort(nums.begin(), nums.end()); // 2、利用双指针解决问题 int ret = 0, n = nums.size(); for(int i = n - 1; i >= 2; --i) { int left = 0, right = i - 1; while(left < right) { // 当 a+b>c ,a下标属于 [left, right-1]时,都能和 b、c 构成三角形 // 当 a+b<=c ,b下标属于[left-1, right]时,都不能和 a、c 构成三角形 if(nums[left] + nums[right] > nums[i]) { ret += right - left; --right; } else ++left; } } // 返回值 return ret; } }; /* - 时间复杂度:O(n^2) - 空间复杂度:O(1) */
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
6. 查找总价格为目标值的两个商品

算法原理

代码编写
class Solution { public: vector<int> twoSum(vector<int>& price, int target) { // 1、数据初始化 int left = 0, right = price.size() - 1; // 2、利用双指针解决问题 while(left < right) { int sum = price[left] + price[right]; if(sum < target) ++left; else if(sum > target) --right; else return {price[left], price[right]}; } // 题目没有明确说明没有结果的话会怎么样,那么该题的测试用例应该都是有结果的 // 为了照顾编译器要求一定要返回一个结果,所以我们最后返回一个空数组即可 return {}; } }; /* - 时间复杂度:O(n) - 空间复杂度:O(1) */
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
7. 三数之和

算法原理
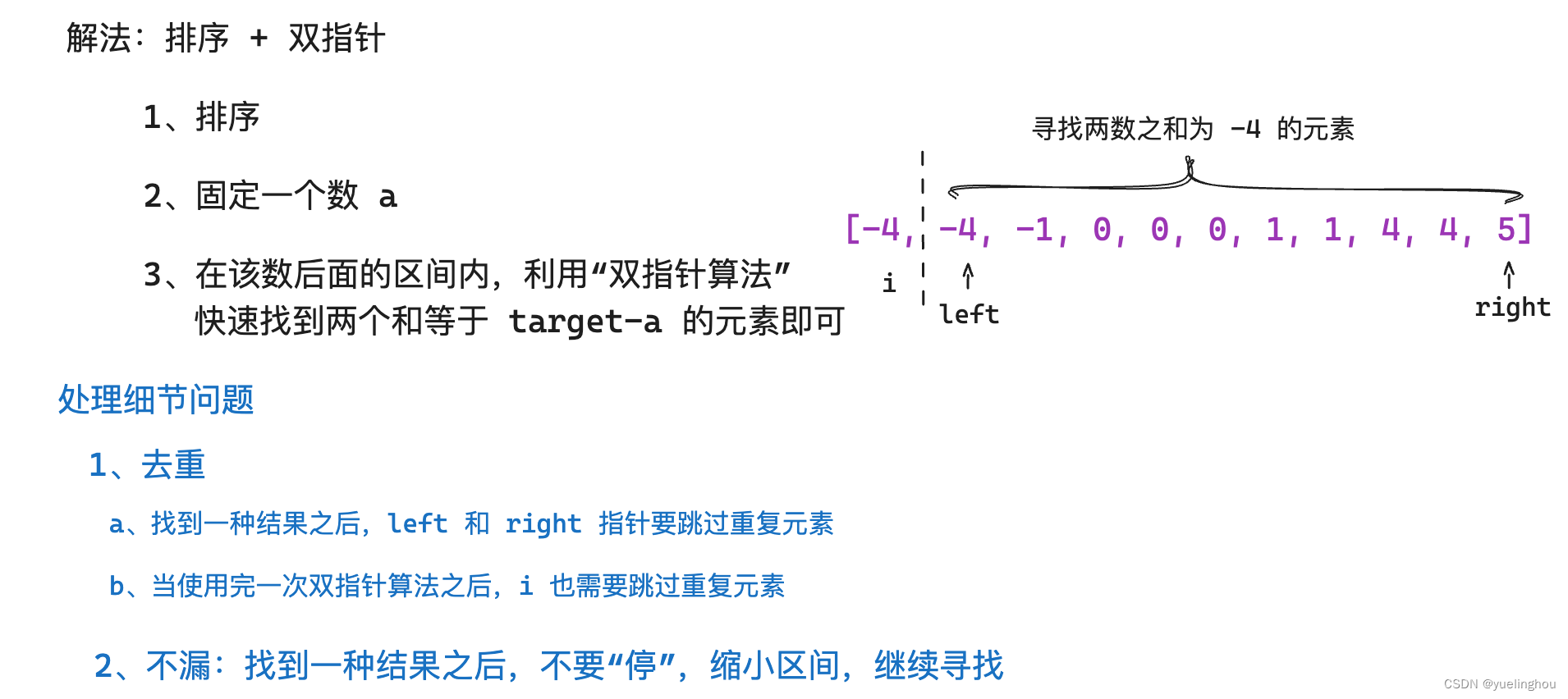
代码编写
class Solution { public: vector<vector<int>> threeSum(vector<int>& nums) { // 1、初始化 int n = nums.size(); vector<vector<int>> ret; // 2、排序 sort(nums.begin(), nums.end()); // 3、依次固定一个数 for(int i = 0; i < n - 2;) { // 4、双指针算法找到两数之和等于 aim 的元素 int left = i + 1, right = n - 1, aim = -nums[i]; while(left < right) { int sum = nums[left] + nums[right]; if(sum < aim) ++left; else if(sum > aim) --right; else { ret.push_back( {nums[i], nums[left], nums[right]} ); ++left, --right; // 保证 left、right 选择的元素不漏 // 对 left、right 已经选择过的元素去重 while(left < right && nums[left] == nums[left - 1]) ++left; while(left < right && nums[right] == nums[right + 1]) --right; } } // 保证 i 选择的元素不漏 ++i; // 对 i 已经选择过的元素去重 while(i < n - 2 && nums[i] == nums[i - 1]) ++i; } // 5、返回最终结果 return ret; } }; /* - 时间复杂度:O(n^2) - 空间复杂度:O(1) */
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
8. 四数之和

算法原理

代码编写
class Solution { public: vector<vector<int>> fourSum(vector<int>& nums, int target) { // 1、初始化 int n = nums.size(); vector< vector<int> > ret; // 2、排序 sort(nums.begin(), nums.end()); // 3、依次固定一个数,然后使用“三数之和”解决问题 for(int i = 0; i < n - 3;) { // 4、再依次固定一个数,然后使用“双指针”解决问题 for(int j = i + 1; j < n - 2;) { int left = j + 1, right = n - 1; double aim = (double)target - nums[i] - nums[j]; // 5、双指针算法找到两数之和等于 aim 的元素 while(left < right) { double sum = nums[left] + nums[right]; if(sum < aim) ++left; else if(sum > aim) --right; else { ret.push_back( {nums[i], nums[j], nums[left], nums[right]} ); ++left, --right; // 保证 left、right 选择的元素不漏 // 对 left、right 已经选择过的元素去重 while(left < right && nums[left] == nums[left - 1]) ++left; while(left < right && nums[right] == nums[right + 1]) --right; } } // 保证 j 选择的元素不漏 ++j; // 对 j 已经选择过的元素去重 while(j < n - 2 && nums[j] == nums[j - 1]) ++j; } // 保证 i 选择的元素不漏 ++i; // 对 i 已经选择过的元素去重 while(i < n - 3 && nums[i] == nums[i - 1]) ++i; } // 6、返回最终结果 return ret; } }; /* - 时间复杂度:O(n^3) - 空间复杂度:O(1) */
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
专题二:滑动窗口
1. 长度最小的子数组

算法原理

代码编写
class Solution { public: int minSubArrayLen(int target, vector<int>& nums) { int sum = 0, len = INT_MAX; for(int left = 0, right = 0; right < nums.size(); ++right) { // 1、进窗口 sum += nums[right]; // 2、判断 && 更新 while(sum >= target) { len = min(len, right - left + 1); sum -= nums[left++]; // 出窗口 } } // 3、返回值 return len == INT_MAX ? 0 : len; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
2. 无重复字符的最长字串

算法原理
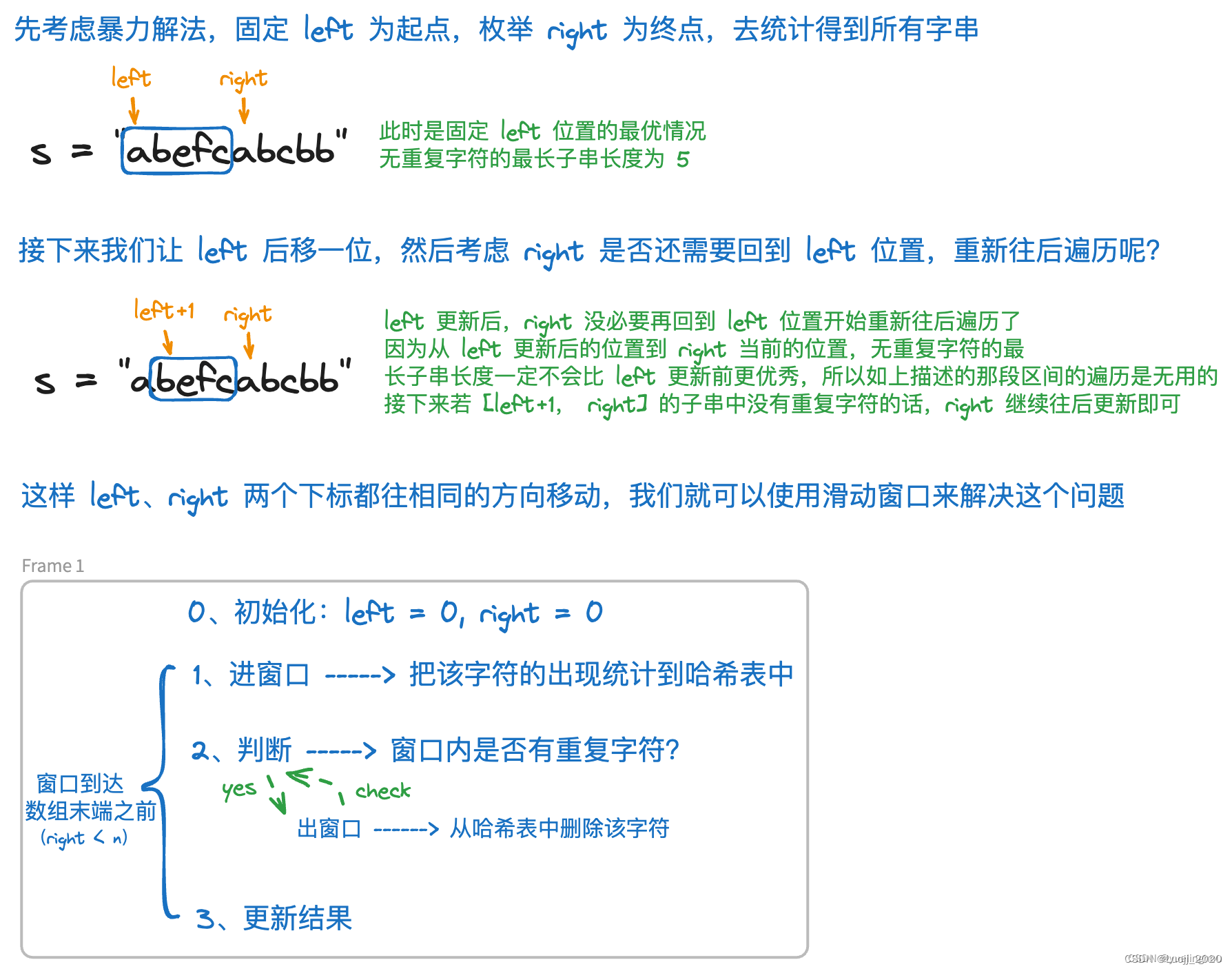
代码编写
class Solution { public: int lengthOfLongestSubstring(string s) { // 1、初始化 int len = 0, n = s.size(); unordered_map<char, int> hash; // 2、滑动窗口 for(int left = 0, right = 0; right < n; ++right) { // 进窗口 ++hash[s[right]]; // 判断 if(hash[s[right]] == 1) len = max(len, right - left + 1); else while(hash[s[right]] > 1) hash[s[left++]]--; } // 3、返回值 return len; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
3. 最大连续 1 的个数III

算法原理

代码编写
class Solution { public: int longestOnes(vector<int>& nums, int k) { // 1、初始化 int len = 0, n = nums.size(); // 2、滑动窗口 for(int left = 0, right = 0; right < n; ++right) { // 进窗口 if(!nums[right]) --k; // 检查 && 更新 if(k >= 0) len = max(len, right - left + 1); while(k < 0) if(nums[left++] == 0) ++k; } // 3、返回值 return len; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
4. 将 x 减到 0 的最小操作数

题目解析
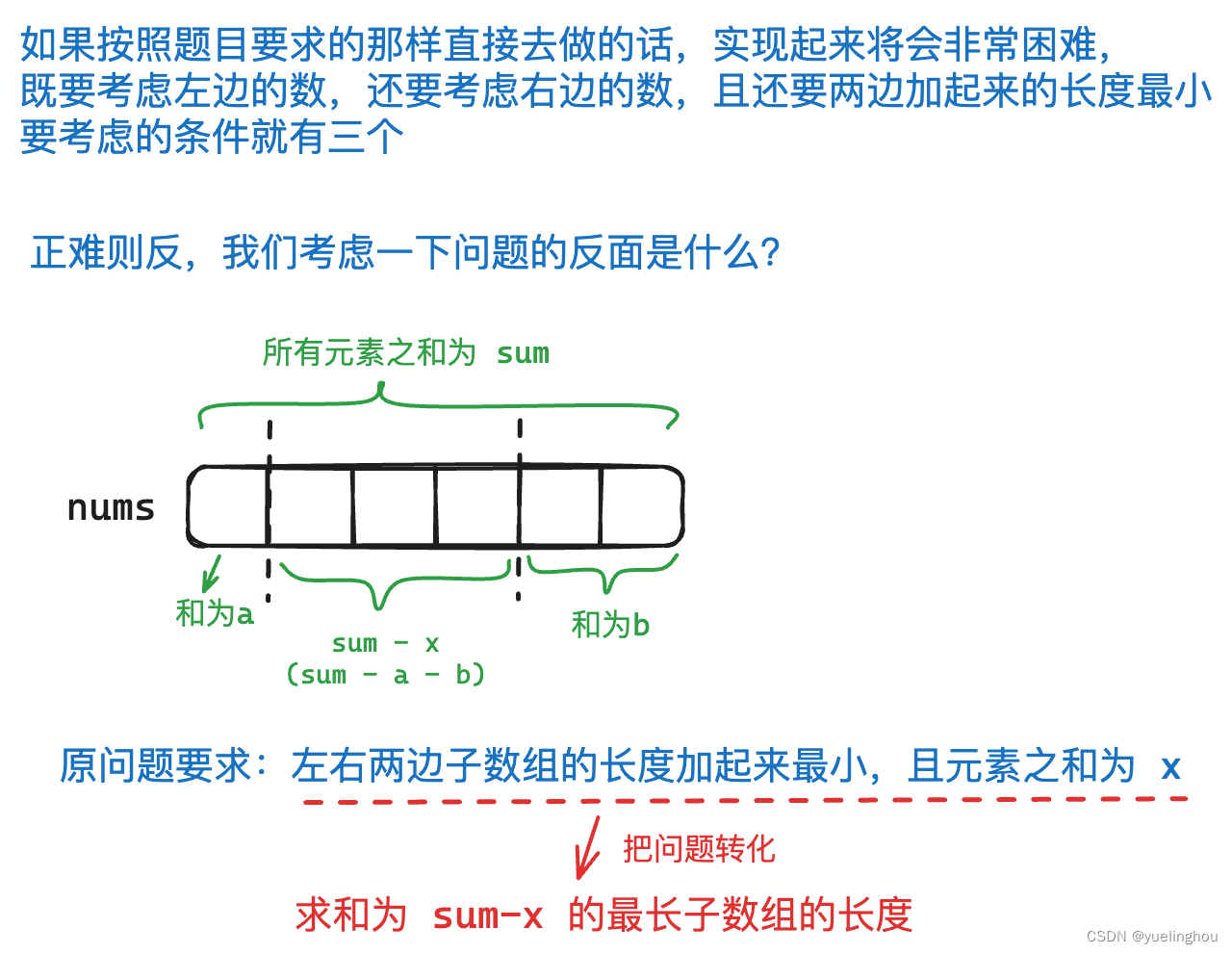
算法原理

代码编写
class Solution { public: int minOperations(vector<int>& nums, int x) { // 1、初始化 int sum = 0; for(const auto e : nums) sum += e; int target = sum - x; // 2、细节处理(数组中所有元素都大于0,所以 target 小于 0 是不存在的) if(target < 0) return -1; // 3、滑动窗口 int ret = -1; for(int left = 0, right = 0, tmp = 0; right < nums.size();) { // 进窗口 tmp += nums[right++]; // 出窗口 while(tmp > target) tmp -= nums[left++]; // 更新结果 if(tmp == target) ret = max(ret, right - left); } // 4、返回结果 return ret == -1 ? ret : nums.size() - ret; } }; /* - 时间复杂度:O(n) - 空间复杂度:O(1) */
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
5. 水果成篮

算法原理
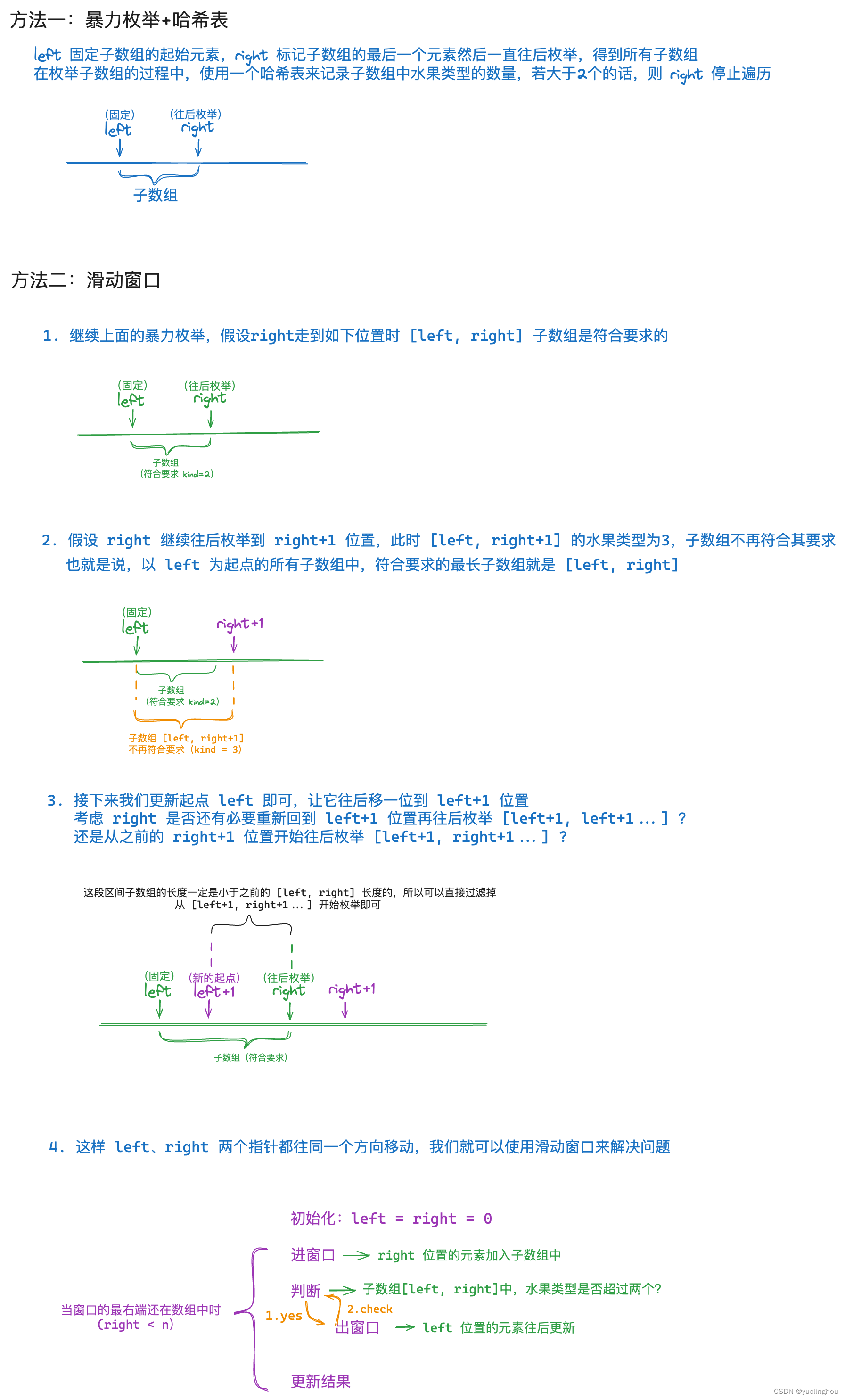
代码编写
class Solution { public: int totalFruit(vector<int>& fruits) { // 1、初始化 int ans = INT_MIN; unordered_map<int, int> hash; // <水果类型, 水果数量> // 2、滑动窗口 for(int left = 0, right = 0; right < fruits.size(); ++right) { // 进窗口 int in = fruits[right]; ++hash[in]; // 判断 while(hash.size() > 2) { // 出窗口 int out = fruits[left++]; if(--hash[out] == 0) hash.erase(out); } // 更新结果 ans = max(ans, right - left + 1); } // 3、返回值 return ans; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
6. 找到字符串中所有字母异位词

算法原理
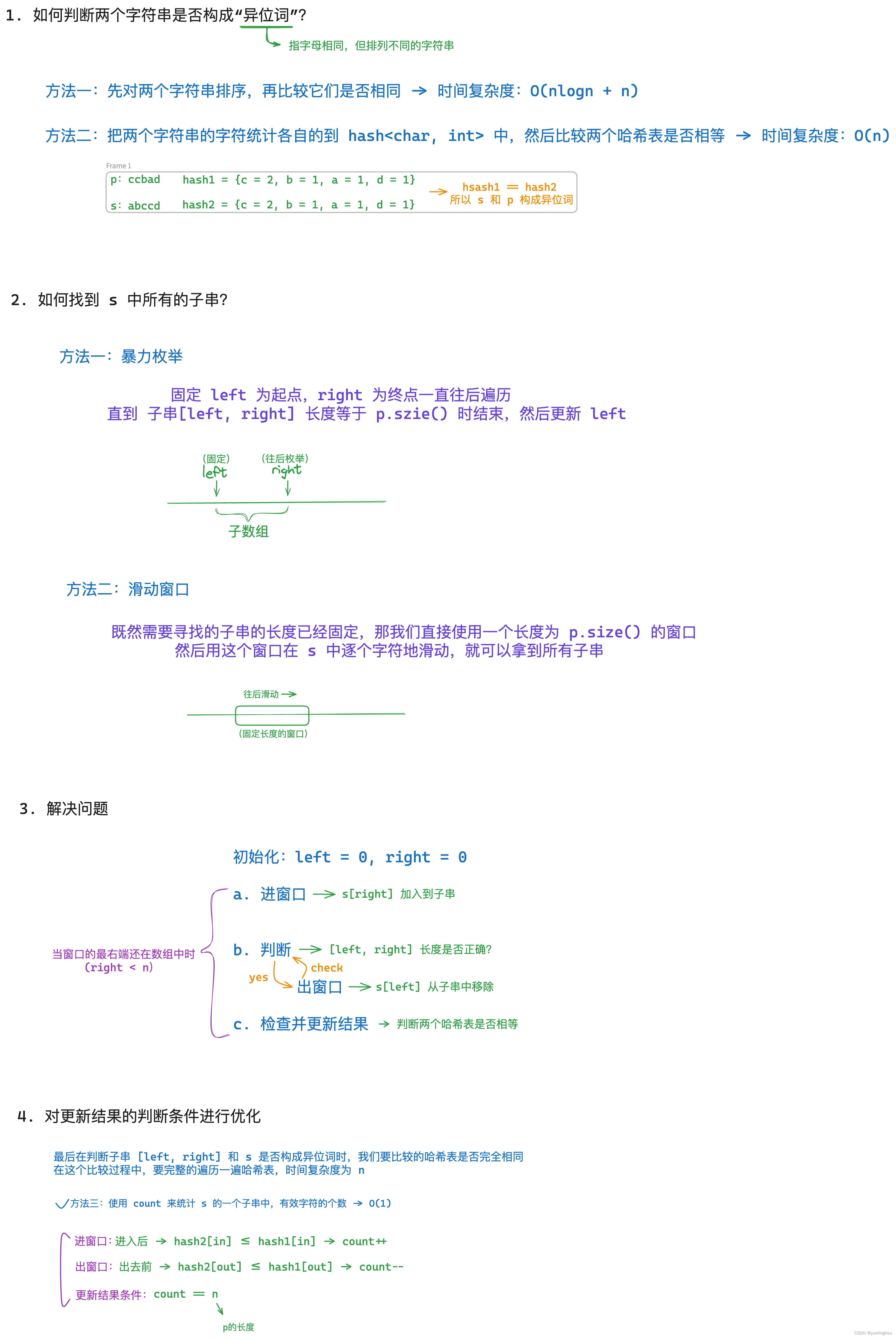
代码编写
class Solution { public: vector<int> findAnagrams(string s, string p) { // 1、初始化 vector<int> ret; int hash1[26] = {0}; //统计 p 中字符出现的次数 int hash2[26] = {0}; //统计窗口中字符出现的次数 for(const auto e : p) ++hash1[e - 'a']; // 2、滑动窗口 for(int left = 0, right = 0, count = 0; right < s.size(); ++right) { // 进窗口 + 维护 count char in = s[right]; if(++hash2[in - 'a'] <= hash1[in - 'a']) ++count; // 判断 while(right - left + 1 > p.size()) { // 出窗口 + 维护 count char out = s[left++]; if(hash2[out - 'a']-- <= hash1[out - 'a']) --count; } // 更新结果 if(count == p.size()) ret.push_back(left); } // 3、返回值 return ret; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
7. 串联所有单词的子串

算法原理

代码编写
class Solution { public: vector<int> findSubstring(string s, vector<string>& words) { // 1、初始化 int n = words.size(), step = words[0].size(); unordered_map<string, int> hash1, hash2; for(const auto& e : words) ++hash2[e]; // 2、滑动窗口 vector<int> ans; for(int i = 0 ; i < step; ++i) { for(int left = i, right = i, count = 0; right + step <= s.size(); right += step) { // 进窗口 string in = s.substr(right, step); if(hash2.count(in) && ++hash1[in] <= hash2[in]) ++count; // 判断 while(((right - left) / step + 1) > n) { string out = s.substr(left, step); if(hash2.count(out) && hash1[out]-- <= hash2[out]) --count; left += step; } // 更新结果 if(count == n) ans.push_back(left); } // 每完成一组滑动窗口,就重置 hash1 hash1.clear(); } // 3、返回值 return ans; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
8. 最小覆盖子串

算法原理
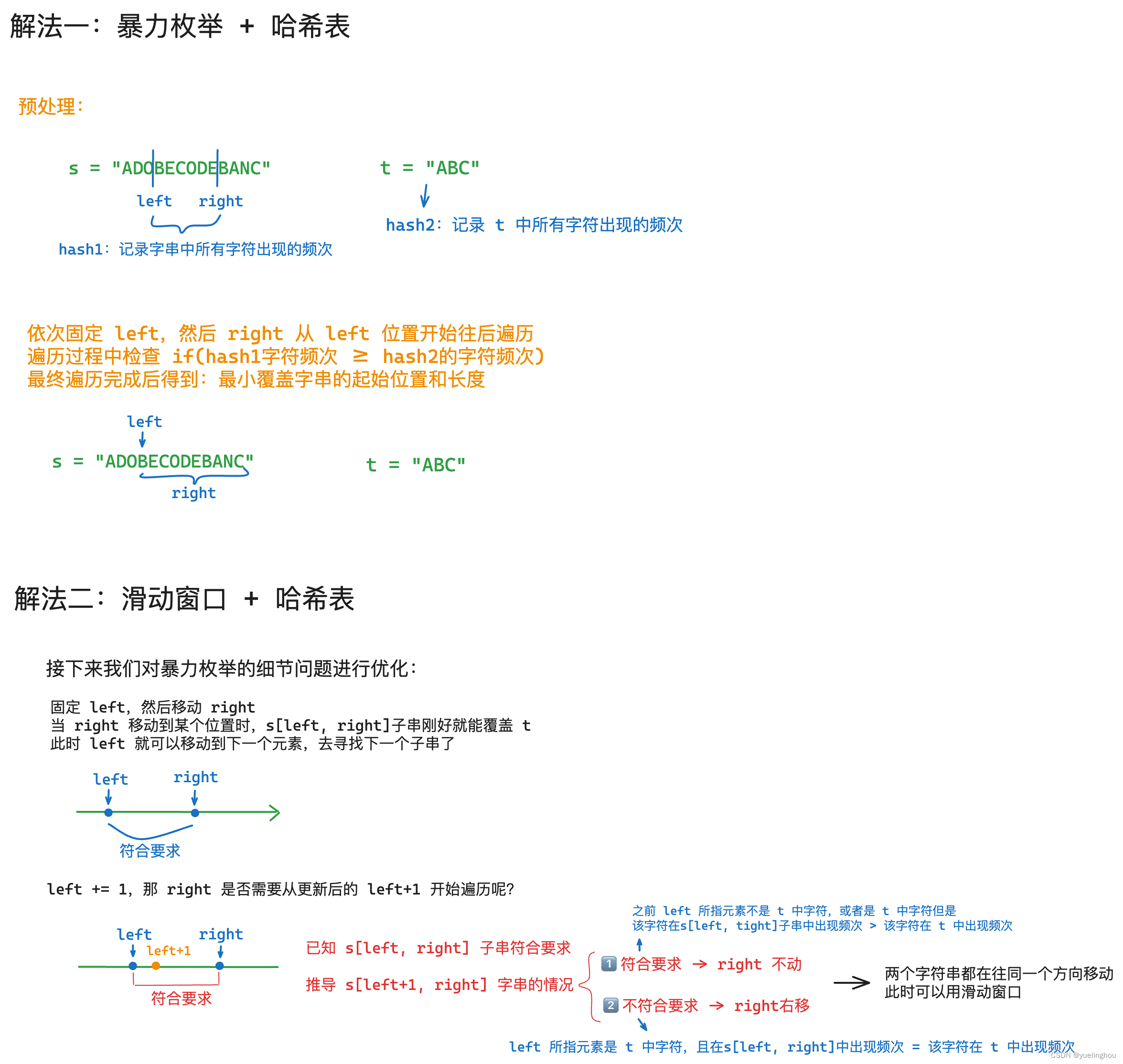
代码编写

class Solution { public: string minWindow(string s, string t) { // 1、初始化(题目说:s 和 t 由英文字母组成,所以我们可以使用定长数组来代替哈希表) int hash1[128] = {0}, hash2[128] = {0}, kind = 0; for(const auto e : t) if(hash2[e]++ == 0) ++kind; // 2、滑动窗口 int begin = -1, len = INT_MAX; for(int left = 0, right = 0, count = 0; right < s.size(); ++right) { // 进窗口 && 更新count char in = s[right]; if(++hash1[in] == hash2[in]) ++count; // 更新count && 出窗口 while(count == kind) { // 更新结果 if(right - left + 1 < len) { begin = left; len = right - left + 1; } char out = s[left++]; if(hash1[out]-- == hash2[out]) --count; } } // 3、返回值 return len == INT_MAX ? "" : s.substr(begin, len); } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
专题三:二分查找

1. 二分查找

算法原理
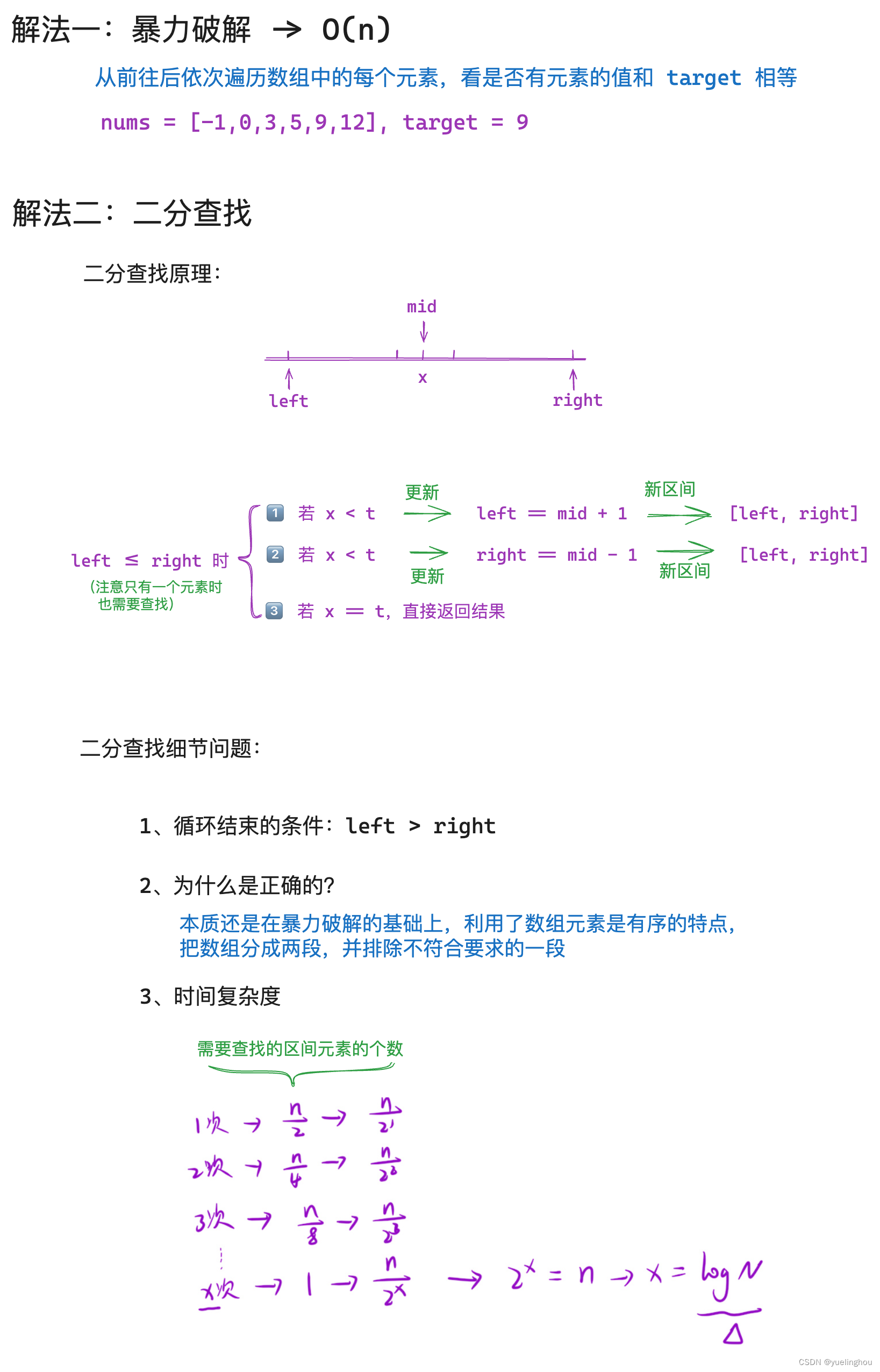
代码编写
class Solution { public: int search(vector<int>& nums, int target) { int left = 0, right = nums.size() - 1; while(left <= right) { int mid = left + (right - left) / 2; //防止溢出 if(nums[mid] < target) left = mid + 1; else if(nums[mid] > target) right = mid - 1; else return mid; } return -1; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
总结朴素二分模板

2. 在排序数组中查找元素的第一个和最后一个位置

算法原理
代码编写
class Solution { public: vector<int> searchRange(vector<int>& nums, int target) { int n = nums.size(); // 特殊情况处理 if(!n) return {-1, -1}; // 1、二分找左端点 int left = 0, right = n - 1, begin = -1; while(left < right) { int mid = left + (right - left) / 2; if(nums[mid] < target) left = mid + 1; else right = mid; } // 2、判断是否有结果 && 标记左端点 if(nums[left] != target) return {-1, -1}; else begin = left; // 3、二分找右端点 right = n - 1; while(left < right) { int mid = left + (right - left + 1) / 2; if(nums[mid] <= target) left = mid; else right = mid - 1; } // 4、返回最终结果 return {begin, right}; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
总结:查找边界的二分模板
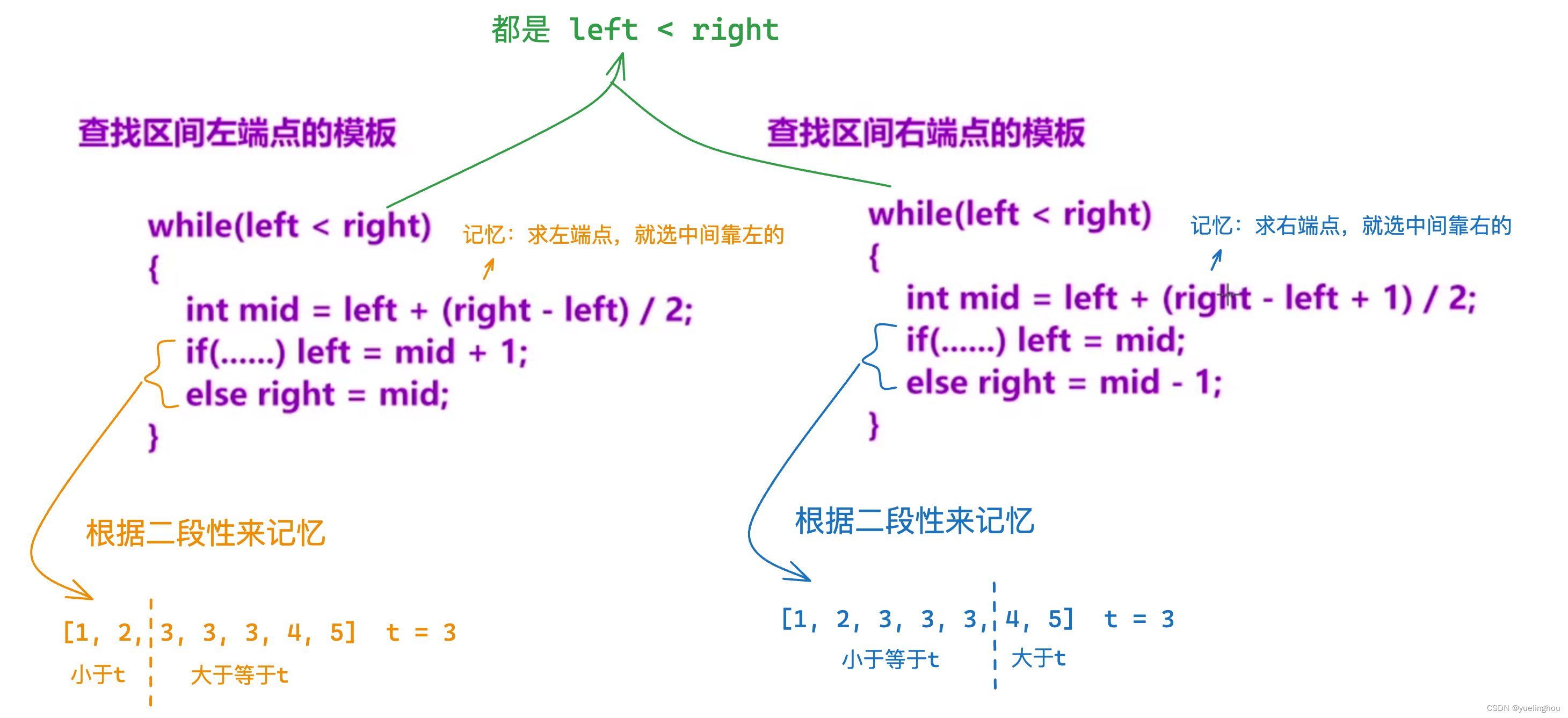
3. X 的平方根

算法原理

代码编写
class Solution
{
public:
int mySqrt(int x)
{
int left = 0, right = x;
while(left < right)
{
long long mid = left + (right - left + 1) / 2;
if(mid * mid <= x) left = mid;
else right = mid - 1;
}
return left;
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
4. 搜索插入位置

算法原理

代码编写
class Solution { public: int searchInsert(vector<int>& nums, int target) { // 1、下标初始化 int left = 0, right = nums.size() - 1; // 2、二分查找大于等于 target 的左边界 while(left < right) { int mid = left + (right - left) / 2; if(nums[mid] < target) left = mid + 1; else right = mid; } // 3、处理最终的返回值 if(nums[left] < target) return left + 1; else return left; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
5. 山脉数组的峰顶索引

题目解析

算法原理

代码编写
class Solution { public: int peakIndexInMountainArray(vector<int>& arr) { // 1、区间下标初始化(注意最两边的元素一点不是最终结果) int left = 1, right = arr.size() - 2; // 2、二叉查找单调递增区间的右边界 while(left < right) { int mid = left + (right - left + 1) / 2; if(arr[mid] > arr[mid - 1]) left = mid; else right = mid - 1; } // 3、返回值 return left; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
6. 寻找峰值

算法原理
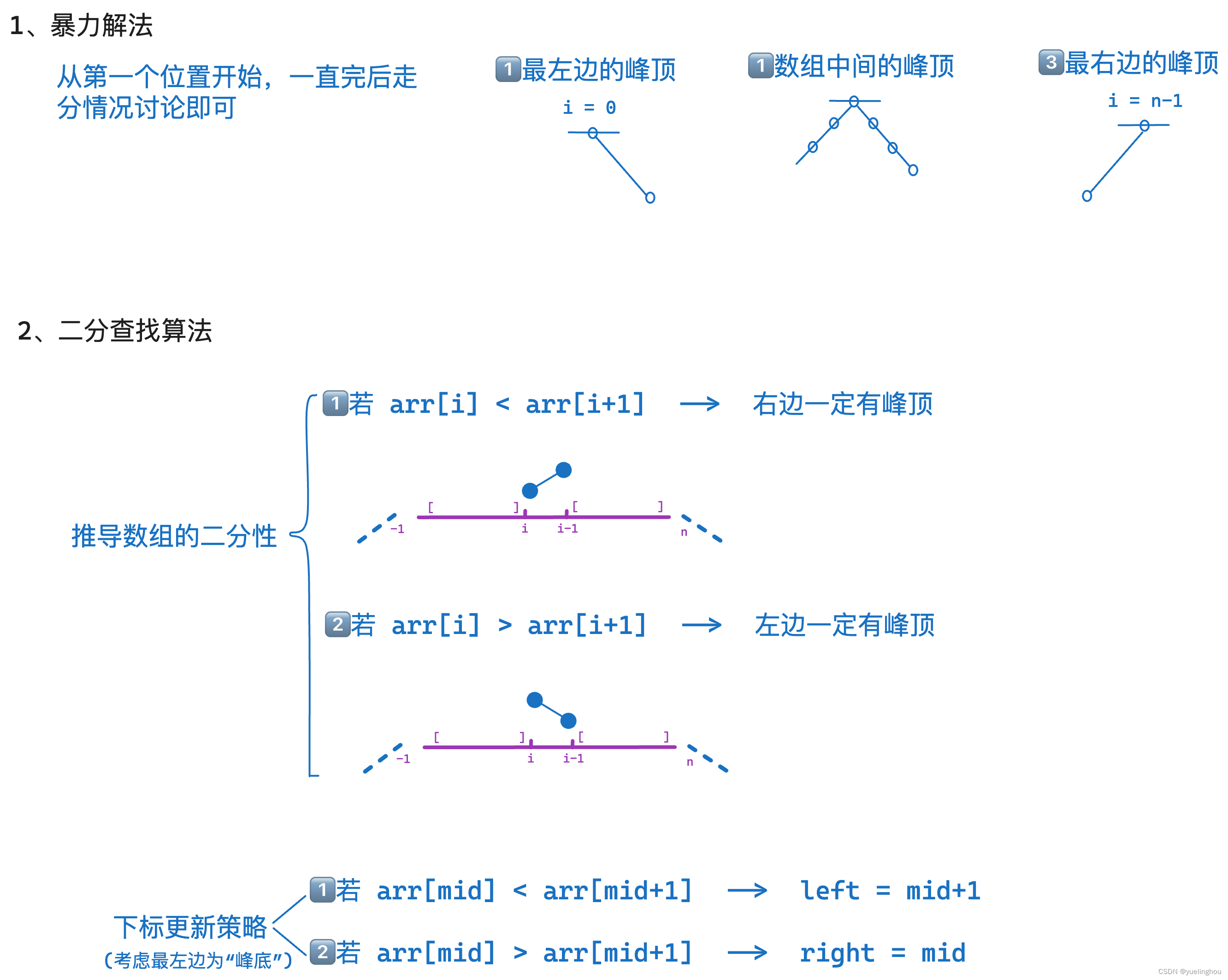
代码编写
class Solution
{
public:
int findPeakElement(vector<int>& nums)
{
int left = 0, right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < nums[mid + 1]) left = mid + 1;
else right = mid;
}
return left;
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
7. 寻找旋转排序数组中的最小值

算法原理

代码编写
class Solution
{
public:
int findMin(vector<int>& nums)
{
int left = 0, right = nums.size() - 1, key = nums[right];
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] > key) left = mid + 1;
else right = mid;
}
return nums[left];
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
8. 点名

算法原理

代码编写
class Solution { public: int takeAttendance(vector<int>& records) { // 二分解法 int left = 0, right = records.size() - 1; while(left < right) { int mid = left + (right - left) / 2; if(records[mid] == mid) left = mid + 1; else right = mid; } // 返回值的时候,注意处理细节问题 return records[left] == left ? left + 1 : left; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
专题四:前缀和
1. 【模板】一维前缀和

算法原理
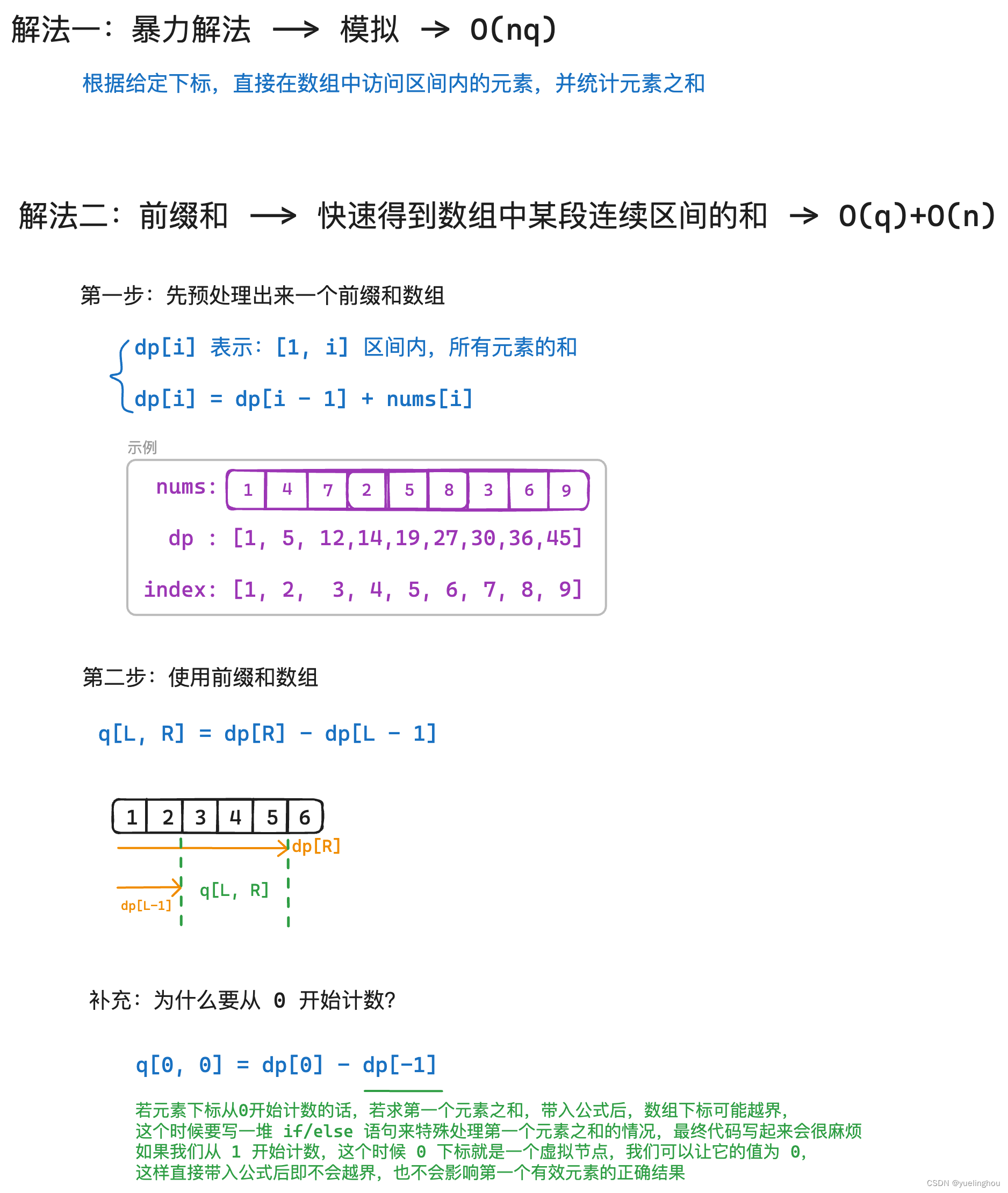
代码编写
#include <iostream> #include <vector> using namespace std; int main() { // 1、读取输入数据 int n = 0, q = 0; cin >> n >> q; vector<int> arr(n + 1); for(int i = 1; i <= n; ++i) cin >> arr[i]; // 2、预处理出来一个前缀和数组 vector<long long> dp(n + 1); for(int i = 1; i <= n; ++i) dp[i] = dp[i - 1] + arr[i]; // 3、使用前缀和数组,直接计算前缀和 for(int l, r; q--;) { cin >> l >> r; cout << dp[r] - dp[l - 1] << endl; } return 0; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
2. 【模板】二维前缀和

算法原理

代码编写
#include <iostream> #include <vector> using namespace std; int main() { // 1、读如数据 int n = 0, m = 0, q = 0; cin >> n >> m >> q; vector<vector<int>> matrix(n + 1, vector<int>(m + 1)); for(int i = 1; i <= n; ++i) for(int j = 1; j <= m; ++j) cin >> matrix[i][j]; // 2、预处理一个前缀和数组 vector<vector<long long>> dp(n + 1, vector<long long>(m + 1)); for(int i = 1; i <= n; ++i) for(int j = 1; j <= m; ++j) dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + matrix[i][j] - dp[i - 1][j - 1]; // 3、使用前缀和数组解决问题 for(int x1, y1, x2, y2; q--;) { cin >> x1 >> y1 >> x2 >> y2; cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] << endl; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
3. 寻找数组的中心下标

算法原理

代码编写
class Solution { public: int pivotIndex(vector<int>& nums) { // 1、初始化 int n = nums.size(); // 2、预处理前/后缀和数组 vector<int> f(n), g(n); for(int i = 1; i < n; ++i) f[i] = f[i - 1] + nums[i - 1]; for(int j = n - 2; j >= 0; --j) g[j] = g[j + 1] + nums[j + 1]; // 3、使用前/后缀合数组 for(int i = 0; i < n; ++i) if(f[i] == g[i]) return i; return -1; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
4. 除自身以外数组的乘积

算法原理

代码编写
class Solution { public: vector<int> productExceptSelf(vector<int>& nums) { int n = nums.size(); // 1、创建前、后缀积数组 vector<int> f(n), g(n); f[0] = g[n - 1] = 1; for(int i = 1; i < n; ++i) f[i] = f[i - 1] * nums[i - 1]; for(int i = n - 2; i >= 0; --i) g[i] = g[i + 1] * nums[i + 1]; // 2、使用前、后缀积数组 vector<int> ret(n); for(int i = 0; i < n; ++i) ret[i] = f[i] * g[i]; // 3、返回结果 return ret; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
5. 和为K的子数组
题目描述
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
PS:子数组是数组中元素的连续非空序列。
示例1
输入:nums = [1,1,1], k = 2
输出:2
示例2
输入:nums = [1,2,3], k = 3
输出:2
提示:
- 1 <= nums.length <= 2 * 104
- -1000 <= nums[i] <= 1000
- -107 <= k <= 107
解题思路
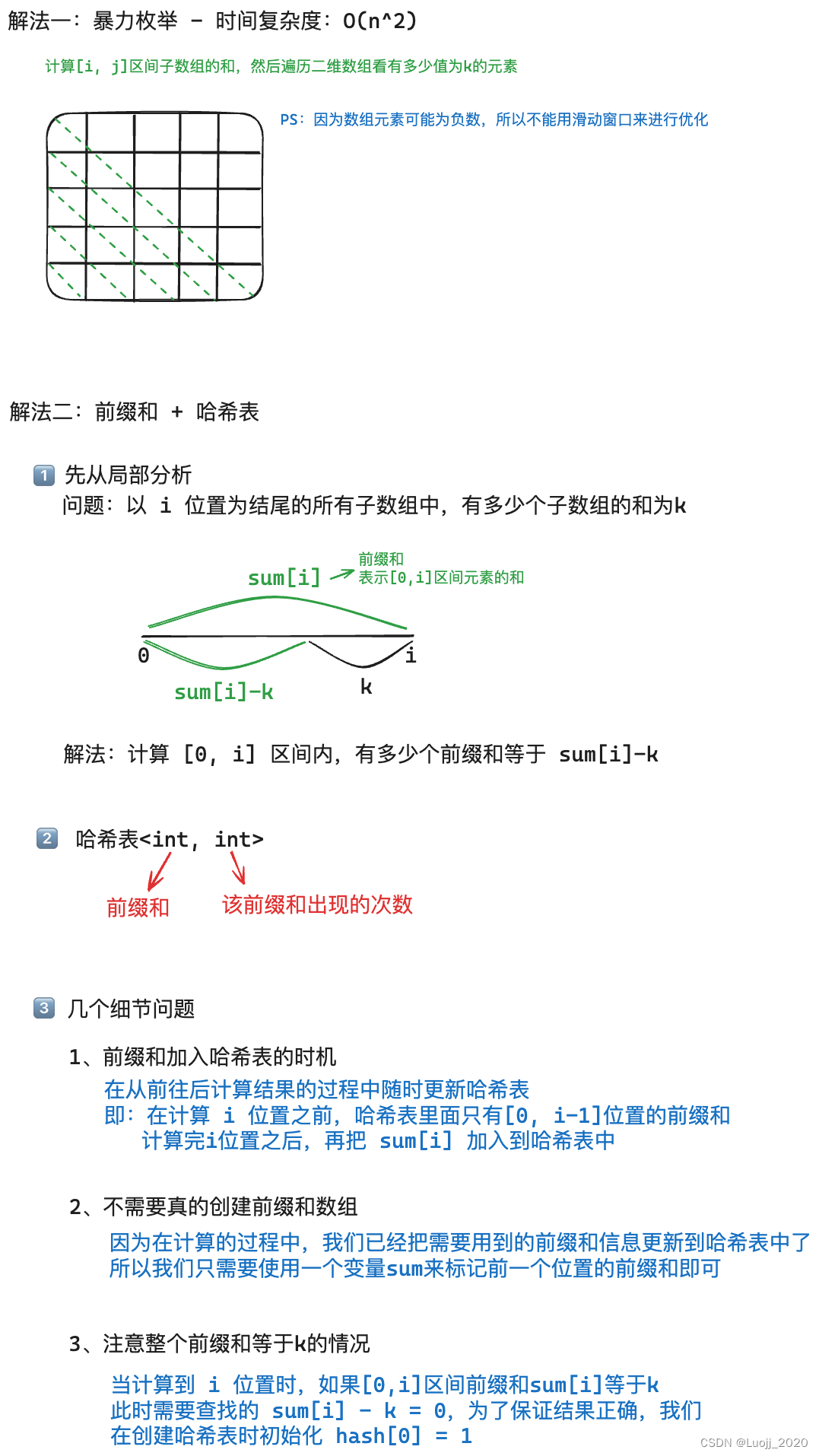
完整代码
class Solution { public: int subarraySum(vector<int>& nums, int k) { // 1、建表 && 初始化 unordered_map<int, int> hash; hash[0] = 1; // 2、哈希表 + 前缀和 int sum = 0, ret = 0; for(const auto e : nums) { sum += e; // 计算当前位置的前缀和 if(hash.count(sum - k)) ret += hash[sum - k]; // 统计结果 ++hash[sum]; // 更新哈希表 } // 3、返回值 return ret; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
6. 和可被 K 整除的子数组
题目描述
给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的(连续、非空) 子数组 的数目。
PS:子数组 是数组的 连续 部分。
示例1
输入:nums = [4,5,0,-2,-3,1], k = 5
输出:7
解释:有 7 个子数组满足其元素之和可被 k = 5 整除:
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
示例2
输入: nums = [5], k = 9
输出: 0
提示
- 1 <= nums.length <= 3 * 104
- -104 <= nums[i] <= 104
- 2 <= k <= 104
完整代码
class Solution { public: int subarraysDivByK(vector<int>& nums, int k) { // 1、建表 && 初始化 unordered_map<int, int> hash; hash[0 & k] = 1; // 2、哈希 + 前缀和 int ret = 0, sum = 0; for(const auto e : nums) { sum += e; // 计算当前位置的前缀和 int remain = (sum % k + k) % k; // 修正后的余数 if(hash.count(remain)) ret += hash[remain]; // 统计结果 ++hash[remain]; // 更新哈希表 } // 3、返回值 return ret; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
7. 连续数组
题目描述
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
示例 1
输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。
示例 2
输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。
提示
- 1 <= nums.length <= 105
- nums[i] 不是 0 就是 1
算法原理
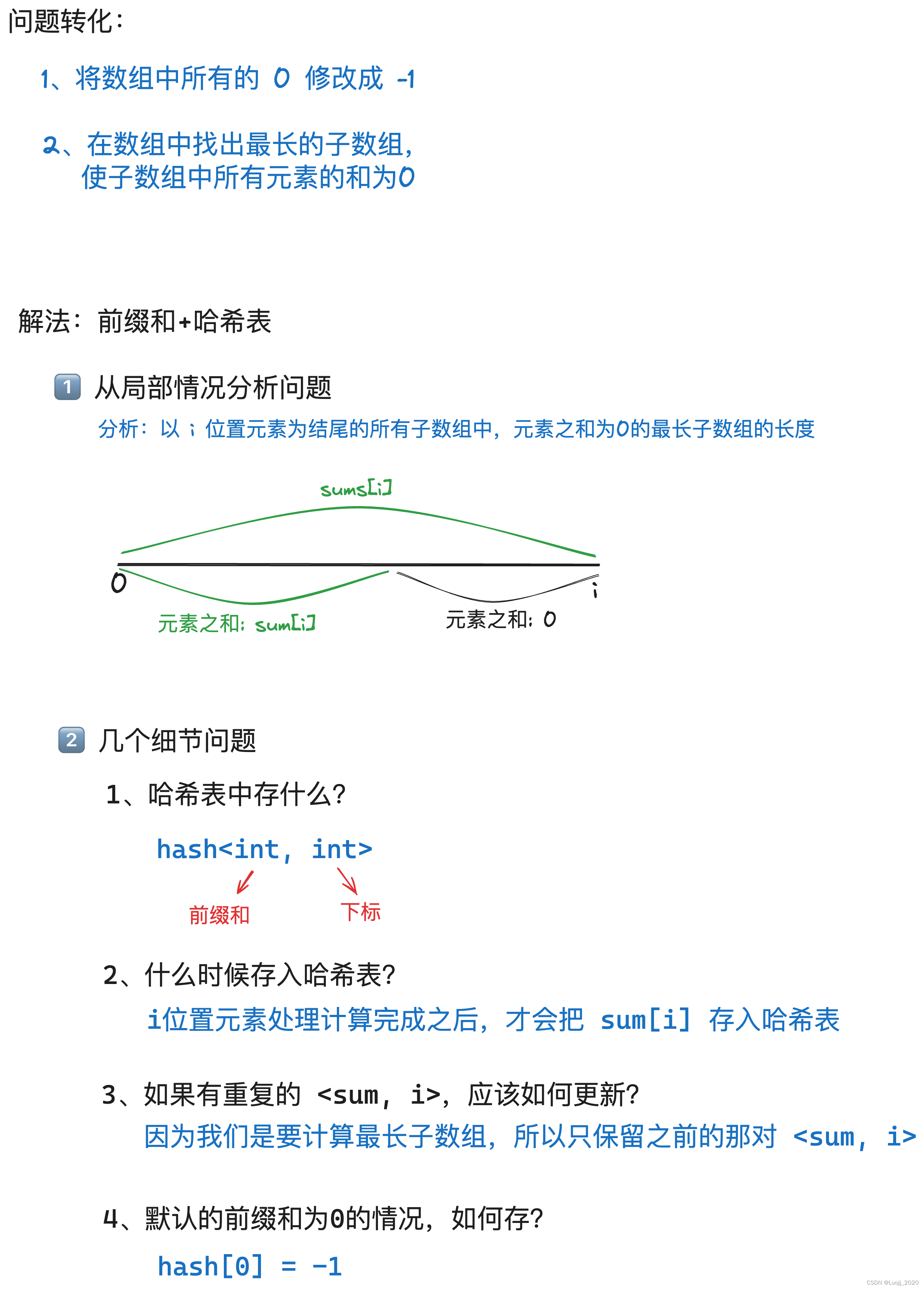
完整代码
class Solution { public: int findMaxLength(vector<int>& nums) { // 1、建表 && 初始化 unordered_map<int, int> hash; hash[0] = -1; // 2、前缀和 + 哈希表 int sum = 0, maxLength = 0; for(int i = 0; i < nums.size(); ++i) { sum += (nums[i] == 0 ? -1 : 1); //计算当前位置的前缀和 if(hash.count(sum)) maxLength = max(maxLength, i - hash[sum]); //更新结果 else hash[sum] = i; //更新哈希表 } // 3、返回值 return maxLength; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
8. 矩阵区域和
题目描述
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
- i - k <= r <= i + k,
- j - k <= c <= j + k 且
- (r, c) 也在矩阵内。
示例 1
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[12,21,16],[27,45,33],[24,39,28]]
示例 2
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出:[[45,45,45],[45,45,45],[45,45,45]]
提示
- m == mat.length
- n == mat[i].length
- 1 <= m, n, k <= 100
- 1 <= mat[i][j] <= 100
题目解析
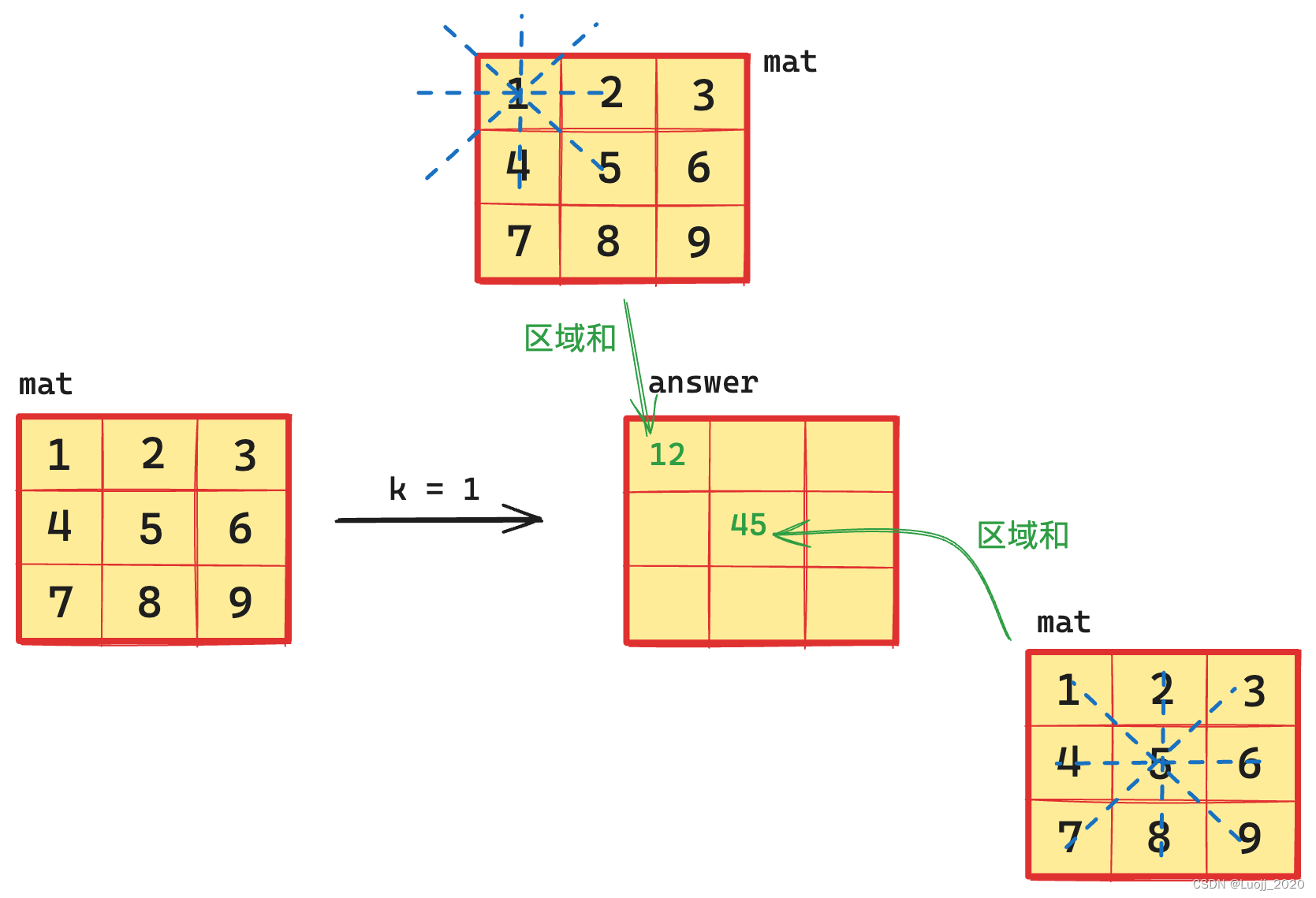
解题思路
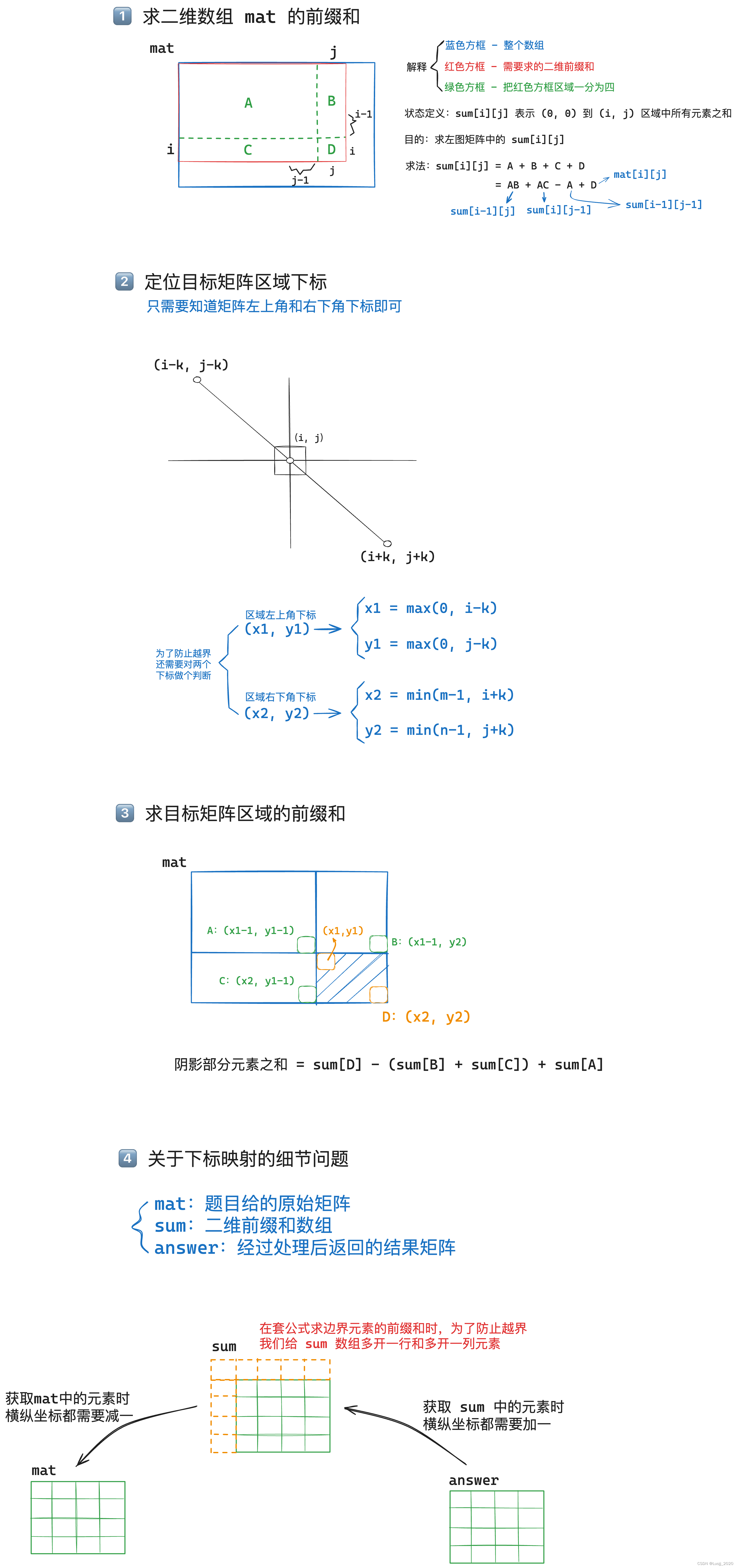
完整代码
class Solution { public: vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) { int m = mat.size(), n = mat[0].size(); // 1、预处理一个矩阵和数组 vector<vector<int>> sum(m + 1, vector<int>(n + 1)); for(int i = 1; i <= m; ++i) for(int j = 1; j <= n; ++j) sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1]; // 2、求矩阵区域和 vector<vector<int>> ans(m, vector<int>(n)); for(int i = 0; i < m; ++i) for(int j = 0; j < n; ++j) { // 计算矩阵左上角和右下角下标 int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1; int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1; // 计算区域元素之和 ans[i][j] = sum[x2][y2] - (sum[x1 - 1][y2] + sum[x2][y1 - 1]) + sum[x1 - 1][y1 - 1]; } // 3、返回值 return ans; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28



