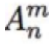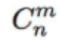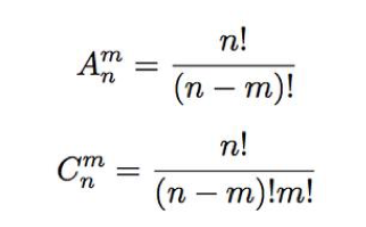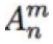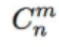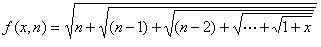山东理工大学：PTA实验七：参考答案与解析（2024）_山东理工大学数据库pta答案_pta吕行军答案

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上大数据知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

需要这份系统化资料的朋友，可以戳这里获取

返回值类型 函数名(形式参数){ 代码 return表达式 } 其中，如果不书写return表达式的话，返回值类型要写void（”空，无”）。 |
| * 参数：分为形式参数和实际参数，没有实际值的参数是形参，有实际值的则为实参。参数的语法是：数据类型 变量名
|
| * 函数的声明：提前让编译器了解到函数的存在。语法是：返回值类型 函数名(形式参数)
|

2.函数可以自己调用自己，这也是递归的一种简单体现

6-2 sdut- C语言实验——矩阵下三角元素之和

1.题目:

输入一个正整数n（1<=n<=10),再输入n*n的矩阵，要求求该矩阵的下三角元素之和。

函数接口定义：

int f(int (*p)[10],int n)；
1

其中 p 和 n 都是用户传入的参数。 p 的值为地址； n 是[1, 10]区间内的个位数。函数不需要返回数据。

裁判测试程序样例：

#include<stdio.h>
int  f(int (*p)[10],int n)；

int main()
{
    int n,i,j,sum;
    int a[10][10];
    scanf("%d",&n);
    for(i=0; i<n; i++)
    {
        for(j=0; j<n; j++)
        {
            scanf("%d",&a[i][j]);
        }
    }
    sum=f(a,n);
    printf("%d",sum);
    return 0;
}


/* 请在这里填写答案 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

输入样例：

5
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
5 6 7 8 9

1
2
3
4
5
6
7

输出样例：

75

1
2

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

2.参考代码:

/*@Keywords of Code:循环的范围、地址传递
  @Author:毛毛maomaonwn
  @Date:2023/12/9
*/


//在解答这题前，需要正确了解“下三角”和“上三角”是什么样的:
/*“下三角”形：
*
**
***
****
  “上三角”形：
****
 ***
  **
   *
*/



int f(int(*p)[10],int n){            //二维数组的传递——指针形式
    int sum = 0;
    for(int i=0;i<n;i++){           
        for(int k=0;k<=i;k++){
            sum+=p[i][k];
        }
    }
    return sum;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

3.解析或补充

1.循环的范围：

数据模拟：

2.二维数组的地址传递——指针形式

函数声明：

void arr_fun(int (*arr)[col],int col);     //1.col代表列数，在多维数组中，第一维是可以省略的。
      

/*2.请注意正确书写（int (*arr)[col]),而不是(int arr[col])。前者是数组的指针，后者是指针数组，它们并不相同。*/
  
1
2
3
4
5

函数调用：

arr_fun(arr,col);

//这里一定是写数组名arr，因为我们是要传递整个数组。
1
2
3

更多的知识：

如果你还想了解直接传递二维数组和传递二级指针的表述，可以参考这篇优秀的博客！二维数组的函数传参分析_二维数组传参-CSDN博客

6-3 sdut-C语言实验- N!

1.题目

给出两个数 n, m。求

和

。
计算公式：

输入数据有多组（数据组数不超过 250），到 EOF 结束。

对于每组数据，输入两个用空格隔开的整数 n, m (0 <= m <= n <= 20) 。
对于每组数据输出一行，

和

，用空格隔开。

提醒：因为n!和 m! 数据较大，定义数据类型应用 long long int，输出格式%lld

函数接口定义：

long long int f(long long int n);
1

其中 n 是用户传入的参数。函数须返回n！的值。

裁判测试程序样例：

#include <stdio.h>
long long int f(long long int n);
int main()
{
    long long int n,m,i;
    while(~scanf("%lld %lld",&n,&m))
    {
        long long int a,c;
        a=f(n)/f(n-m);
        c=f(n)/f(n-m)/f(m);
        printf("%lld %lld\n",a,c);
    }
    return 0;
}

/* 请在这里填写答案 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

输入样例：

在这里给出一组输入。例如：

1 1
5 3
4 3

1
2
3
4

输出样例：

在这里给出相应的输出。例如：

1 1
60 10
24 4

1
2
3
4

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

2.参考代码

long long int f(long long int n){
    int out = 1; 
    for(int i=1;i<=n;i++){
        out*=i;
    }

    return out;
}
1
2
3
4
5
6
7
8

6-4 sdut-C语言实验-使用函数验证哥德巴赫猜想

1.题目

本题要求实现一个判断素数的简单函数，并利用该函数验证哥德巴赫猜想：任何一个不小于6的偶数均可表示为两个奇素数之和。素数就是只能被1和自身整除的正整数。输入一个不小于6的偶数n，找出两个素数，使它们的和为n。注意：1不是素数，2是素数。

函数接口定义：

int isPrime( int x ); 
void Goldbach( int n );
1
2

其中函数isPrime当用户传入参数x为素数时返回1，否则返回0；函数Goldbach按照格式“n=p+q”输出n的素数分解，其中p≤q均为素数。又因为这样的分解不唯一（例如24可以分解为5+19，还可以分解为7+17），要求必须输出所有解中p最小的解。

裁判测试程序样例：

#include <stdio.h>
int isPrime( int x );
void Goldbach( int n );
int main()
{
    int n;
    scanf("%d",&n);
    if(n%2==0)
        Goldbach( n );
    return 0;
}

/* 请在这里填写答案 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14

输入样例：

80

1
2

输出样例：

80=7+73

1
2

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

2.参考代码

/*@Keywords of Code:素数的算法、理解哥德巴赫猜想
  @Author:毛毛maomaonwn
  @Date:2023/12/15 */
                    



int isPrime(int x){
    int judge = 1;                                          //素数的算法:原理见下
    for(int i=2;i<x/2;i++){          
        if(x%i==0){
            judge = 0;
            break;                                          
        }
    }

    return judge;
}



void Goldbach(int n){
    for(int i=3;i<n;i++){                                  //从3开始循环是因为是求"奇素数"
        if(isPrime(i)==1 && isPrime(n-i)==1){
            printf("%d=%d+%d",n,i,n-i);
            break;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

3.解析或补充

1.break语句：

使跳出当前循环。如果是嵌套循环，则跳出最近的循环。

2.素数的算法：

6-5 sdut-C语言实验- 求数列的和

1.题目

数列的定义如下： 数列的第一项为n，以后各项为前一项的平方根，求数列的前m项的和。
提示：因为自定义函数中用到数学函数，因此本题目的提交答案需要包括头文件在内的主函数和自定义函数。

函数接口定义：

double s(double n,int m);
1

其中 n 和 m 都是用户传入的参数。 n 的值不超过double的范围； m 的值不超过int的范围。函数须返回数列前m项的和。

**提示：**本题需要在自定义函数中使用sqrt()数学函数，因此在填写答案时需要提交完整的程序，既题目已经给定的代码部分和需要填写的答案部分。

裁判测试程序样例：

#include <stdio.h>
#include <math.h>

double s(double n,int m);

int main()
{
    int a,b,m,i;
    double sum,n;
    while (scanf("%lf %d",&n,&m)!=EOF)
    {
        sum=s(n,m);
        printf("%.2lf\n",sum);
    }

    return 0;
}


/* 请在这里填写答案 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

输入样例：

81 4
2 2

1
2
3

输出样例：

94.73
3.41

1
2
3

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

2.参考代码

/*@Keywords of Code:sqrt函数
  @Author:毛毛maomaonwn
  @Date:2023/12/15 */



#include <stdio.h>
#include <math.h>

double s(double n,int m);

int main()
{
    int a,b,m,i;
    double sum,n;
    while (scanf("%lf %d",&n,&m)!=EOF)
    {
        sum=s(n,m);
        printf("%.2lf\n",sum);
    }

    return 0;
}

double s(double n,int m){
    double sum = 0;

    for(int i=0;i<m;i++){
        sum+=n;
        n=sqrt(n);
    }

    return sum;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

3.解析或补充

1.pow函数和sqrt函数

6-6 递归实现顺序输出整数

1.题目

本题要求实现一个函数，对一个整数进行按位顺序输出。

函数接口定义：

void printdigits( int n );
1

函数printdigits应将n的每一位数字从高位到低位顺序打印出来，每位数字占一行。

裁判测试程序样例：

#include <stdio.h>

void printdigits( int n );

int main()
{
    int n;
    
    scanf("%d", &n);
    printdigits(n);

    return 0;
}

/* 你的代码将被嵌在这里 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

输入样例：

12345

1
2

输出样例：

1
2
3
4
5

1
2
3
4
5
6

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

2.参考代码

/*@Keywords of Code:递归
  @Author:毛毛maomaonwn
  @Date:2023/12/15 */


//该题标题为“递归实现顺序输出整数”，因此以下我们使用递归的方式来解决

void printdigits(int n){

    if(n/10==0){                    //包含数字是0的特殊情况
        printf("%d\n",n);
        return;
    }

    printdigits(n/10);
    printf("%d\n",n%10);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

3.解析或补充

1.递归

• 将复杂的事物分解为简单的重复的思想
• 书写递归的步骤（思考的顺序可以变化）：1.函数功能，2.递归结束条件，3.递归传递表达式

7-1 sdut- C语言实验—计算表达式

1.题目

计算下列表达式值：

输入格式:

输入x和n的值，其中x为非负实数，n为正整数。

输出格式:

输出f(x,n)，保留2位小数。

输入样例:

3 2

1
2

输出样例:

在这里给出相应的输出。例如：

2.00

1
2

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

2.参考代码

/*@Keywords of Code:理解表达式
  @Author:毛毛maomaonwn
  @Date:2023/12/17 */

#include<stdio.h>
#include<math.h>

double culc(double x,int n);

int main(){
    double x;
    int n;
    double out;
    scanf("%lf %d",&x,&n);



    out = culc(x,n);
    

    
    printf("%.2lf",out);
    
}

double culc(double x,int n){            //可以根据代码列一遍数据来理解

    if(n==1){
        return sqrt(1+x);
    }

    return sqrt(n+culc(x,n-1));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

7-2 sdut-C语言实验- 计算题

1.题目

一个简单的计算，你需要计算f(m,n)，其定义如下：
当m=1时，f(m,n)=n；
当n=1时，f(m,n)=m；
当m>1,n>1时，f(m,n)= f(m-1,n)+ f(m,n-1)

输入格式:

第一行包含一个整数T（1<=T<=100），表示下面的数据组数。
以下T行，其中每组数据有两个整数m，n（1<=m，n<=2000），中间用空格隔开。

输出格式:

对每组输入数据，你需要计算出f(m,n)，并输出。每个结果占一行。

输入样例:

在这里给出一组输入。例如：

2
1 1
2 3

1
2
3
4

输出样例:

在这里给出相应的输出。例如：

1
7

1
2
3

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

2.参考代码

/*@Keywords of Code:基础运用
  @Author:毛毛maomaonwn
  @Date:2023/12/17 */

#include<stdio.h>

int func(int m,int n);

int main(){
    int T;
    int m,n;
    scanf("%d",&T);

    while(T--){                        //输入多组数据
        scanf("%d %d",&m,&n);

        printf("%d\n",func(m,n));       
    }

    return 0;
}

int func(int m,int n){
    if(m==1){
        return n;
    }
    else if(n==1){
        return m;
    }
    else if(m>1 && n>1){
        return func(m-1,n)+func(m,n-1);
    }
    else return;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

3.解析或补充

1.循环条件：while(n)与while(n–)

7-3 sdut-C语言实验-斐波那契数列

1.题目

编写计算斐波那契（Fibonacci）数列的第n项函数fib（n）(n < 40)。
数列描述：
f1=f2==1;
fn=fn-1+fn-2(n>=3)。

输入格式:

输入整数 n 的值（0 < n < 40)。

输出格式:

输出fib(n)的值。

输入样例:

7

1
2

输出样例:

13

1
2

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

2.参考代码

/*@Keywords of Code:理解斐波那契数列
  @Author:毛毛maomaonwn
  @Date:2023/12/17 */

#include<stdio.h>


int main(){
    int n;
    scanf("%d",&n);

    printf("%d",fib(n));

    
    return 0;
}

int fib(int n){
    if(n==1){
        return 1;
    }
    else if(n==2){
        return 1;
    }
    else{
        return fib(n-1)+fib(n-2);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

7-4 求组合数

1.题目

本题要求编写程序，根据公式Cnm​=m!(n−m)!n!​算出从n个不同元素中取出m个元素（m≤n）的组合数。

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化资料的朋友，可以戳这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

n-2(n>=3)。

输入格式:

输入整数 n 的值（0 < n < 40)。

输出格式:

输出fib(n)的值。

输入样例:

7

1
2

输出样例:

13

1
2

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

2.参考代码

/*@Keywords of Code:理解斐波那契数列
  @Author:毛毛maomaonwn
  @Date:2023/12/17 */

#include<stdio.h>


int main(){
    int n;
    scanf("%d",&n);

    printf("%d",fib(n));

    
    return 0;
}

int fib(int n){
    if(n==1){
        return 1;
    }
    else if(n==2){
        return 1;
    }
    else{
        return fib(n-1)+fib(n-2);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

7-4 求组合数

1.题目

本题要求编写程序，根据公式Cnm​=m!(n−m)!n!​算出从n个不同元素中取出m个元素（m≤n）的组合数。

[外链图片转存中…(img-2veHIA8j-1715081927266)]
[外链图片转存中…(img-OpL2ro4p-1715081927267)]

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化资料的朋友，可以戳这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！