【神秘海域】[动图] 数据结构与算法初探：复杂度详解分析 「附代码」_数据结构复杂度分析代码

---

---

复杂度 引言

本篇文章是 数据结构与算法 正式内容的第一篇文章。
要介绍的也是数据结构与算法中最重要的概念之一：复杂度

复杂度，是贯穿整个数据结构与算法学习的一个重要概念。

它是衡量一个算法好坏的重要指标，它包括两个维度：时间、空间，被称为 时间复杂度、空间复杂度。
时间复杂度 主要衡量一个算法的运行快慢
空间复杂度 主要衡量一个算法运行所需要的额外空间

算法的复杂度，一般与需要处理的数据量挂钩，如果数据量为 N，那复杂度就有可能是：N 、 logN 、N*logN 、N^2 等等。

究竟什么是复杂度？

时间复杂度

上面提到：时间复杂度 主要衡量一个算法的运行快慢。
但是，这里的 快慢 并不是指 算法运行所需要执行的具体的时间。而是指：算法中的基本操作的执行次数。并且，算法的时间复杂度用一个函数表示.

举个简单的例子：

// 一个简单的循环
void Fun1(int n)
{
	for(int i = 0; i < n; i++)
	{
		printf("%d ", i);
	}
}
1
2
3
4
5
6
7
8

这段代码，for 循环执行的次数，是根据传入的参数来具体决定的，即循环 n 次。就可以说，这个函数的 时间复杂度是 O(N)。

看起来非常简单？

那么再看一个例子：

void Fun2(int n)
{
	int count = 0;  
	for (int i = 0; i < N ; ++ i)  
	{  
		for (int j = 0; j < N ; ++ j)  
		{  
			++count;  
		}  
	}  
	
	for (int k = 0; k < 2 * N ; ++ k)  
	{  
		++count;  
	}  
	
	int M = 10;  
	while (M--)  
	{  
		++count;  
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

函数 Fun2 中存在三个循环体，其中一个是嵌套的双重循环
那么，这个函数的 时间复杂度 是多少呢？该怎么计算？

逐个分析：

int count = 0;  
for (int i = 0; i < N ; ++ i)  
{  
	for (int j = 0; j < N ; ++ j)  
	{  
		++count;  
	}  
}  
1
2
3
4
5
6
7
8

这个循环是一个循环的嵌套，执行次数是 N*N

for (int k = 0; k < 2 * N ; ++ k)  
{  
	++count;  
}  
1
2
3
4

这个循环就是一个普通的循环，执行次数是 2*N

int M = 10;  
while (M--)  
{  
	++count;  
}
1
2
3
4
5

这个循环是 可以确定次数的循环，每次函数调用执行的次数是一定的，执行次数是 10 次

结合起来，这个函数的时间复杂度就是 O(N^2 + 2*N + 10)
但是，事实并不是这样的。
这个函数的时间复杂度 其实是 O(N^2)
为什么？

来进行一个计算：

• N = 10， 执行次数：10*10 + 2*10 + 10 = 130
• N = 100， 执行次数：100*100 + 2*100 + 10 = 10210
• N = 1000， 执行次数：1000*1000 + 2*1000 + 10 = 1002010
• N = 10000， 执行次数：10000*10000 + 2*10000 + 10 = 100020010

有没有发现什么规律？
随着 N 的增大，2*N + 10 在最终执行次数中的 占比越来越小 了，也代表着 其对最终执行次数的 影响越来越小 了
2*N + 10 在结果中的占比： 23% -> 2% -> 0.2% -> 0.02%

当 N 足够大的时候，就已经可以忽略 2*N + 10 的影响了，所以只需要计算 N^2 就能够代表函数的执行次数，所以 函数 Fun2 的时间复杂度 其实是 O(N^2)。

这时候计算时间复杂度，就只是计算了大概了执行次数，使用的是大 0 的渐进表示法

大 O 的渐进表示法

大O符号（Big O notation）：是用于描述函数渐进 行为 的数学符号
1

用 大O表示法 计算复杂度的方法一般有：

1. 基本操作的执行次数中，相加的常数一般用 1 取代
   即：N^2 + 2*N + 10 —> N^2 + 2*N + 1
   或： O(100) —> O(1)，即常数的时间复杂度，均计算为 O(1)
2. 在常数转后之后的执行次数函数中，取最高次幂项作为时间复杂度，
   即： O(N^2 + 2*N + 1) —> O(N^2)
3. 如果转换后的执行次数函数中，存在 最高次幂项 且 此项不为1，则只保留单个此项作为时间复杂度(即放弃与其相乘的常数)
   即：O(4 * N^2) —> O(N^2)

即，大O的渐进表示法 去掉了那些对结果影响不大的项 ，简洁明了的表示出了时间复杂度。
所以 函数Fun2 的时间复杂度为： O(N^2) 忽略了 2*N + 10

时间复杂度的最好、最坏、平均情况

虽然知道了 大O渐进表示法 的计算方法，但是 总有一些算法代码是拥有多种情况的。
比如：

//查找整型数组中第一个 10 的位置
int Find_10(int *arr, int arrSize)
{
	int i = 0;
	while(arrSize--)
	{
		if(*arr == 10)
		{
			return i;	
		}
		arr++;
		i++;
	}

	return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

这个函数目的是寻找数组中第一个 10 的位置，但是 第一个 10 有可能出现在 一个数组中的任何位置，甚至不出现在数组中。

可能是 在 arr[0] arr[n - 1] arr[n / 2] ，被查找的数的位置是不定的，所以 这个函数中 基本操作的执行次数也是不定的。

那么这个时候，一个算法的时间复杂度，就用最坏情况下的复杂度来表示
Find_10 这个函数的时间复杂度，实际就是 O(N)。

「PS:计算基本操作的执行次数，结果中的未知数用 N 或 M 代表(只有一个未知数 用 N,两个未知数 用 N 和 M, 多个可以用其他)」

时间复杂度计算举例

// 计算Func1的时间复杂度？  
void Func1(int N)  
{  
	int count = 0;  
	for (int k = 0; k < 2 * N ; ++k)  
	{  
		++count;  
	}
	
	int M = 10;  
	while (M--)  
	{  
		++count;  
	}  
	printf("%d\n", count);  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

此函数，通过分析
拥有两个循环体，一个循环 2*N 次，另一个循环 10 次
按照 大O 渐进表示法，时间复杂度为 O(N)

// 计算Func2的时间复杂度？  
void Func2(int N, int M)  
{  
	int count = 0;  
	for (int k = 0; k < M; ++k)  
	{  
		++count;  
	}  
	for (int k = 0; k < N ; ++ k)  
	{  
		++count;  
	}  
	printf("%d\n", count);  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

此函数，通过分析
拥有两个循环体，一个循环 M 次，另一个循环 N 次
按照 大O 渐进表示法，时间复杂度为 O(M + N)

// 计算Func3的时间复杂度？  
void Func3(int N)  
{  
	int count = 0;  
	for (int k = 0; k < 100; ++k)  
	{  
		++count;  
	}  
	printf("%d\n", count);  
}
1
2
3
4
5
6
7
8
9
10

此函数，通过分析
有一个循环体，但是循环体循环次数与传入参数无关，固定循环 100 次
按照 大O 渐进表示法，时间复杂度为 O(1)

// 计算BubbleSort的时间复杂度？  
void BubbleSort(int* a, int n)  
{  
	assert(a);  
	
	for (size_t end = n; end > 0; --end)  
	{  
		int exchange = 0;  
		for (size_t i = 1; i < end; ++i)  
		{  
			if (a[i-1] > a[i])  
			{  
				Swap(&a[i-1], &a[i]); 
				exchange = 1;  
			}  
		}  
		if (exchange == 0)  
			break;  
	}  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

此函数为冒泡排序（排升序）
需要分情况分析：
最好的情况是：除了第一位其他都已位升序，则只需要循环 N 次，即 将第一位数据冒泡至最后一位
最坏的情况是：数据按照降序排列，则每一个数据都要进行排序，计算执行次数的结果为：(N*(N+1)/2 次
按照 大O 渐进表示法，取最坏的情况时间复杂度为 O(N^2)

// 计算BinarySearch的时间复杂度？  
int BinarySearch(int* a, int n, int x)  
{  
	assert(a);  
	
	int begin = 0;  
	int end = n-1;  
	while (begin < end)  
	{  
		int mid = begin + ((end-begin)>>1);  
		if (a[mid] < x)  
			begin = mid+1;  
		else if (a[mid] > x)  
			end = mid;  
		else  
			return mid;  
	}  
	
	return -1;  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

此函数为二分查找，(被查找的数据必须是有序的)
同样需要分情况分析：
最好的情况：指定数据在数组中间位置，只需要执行一次，即第一次查找就查找到指定数据
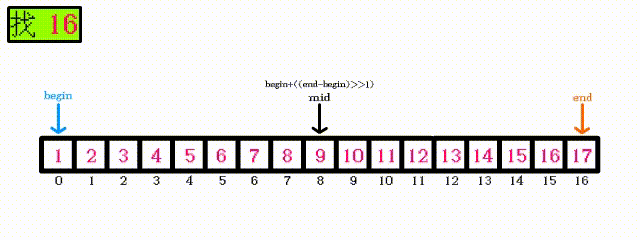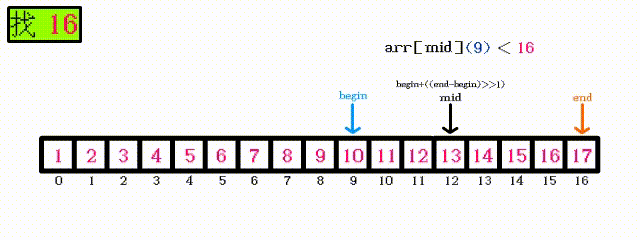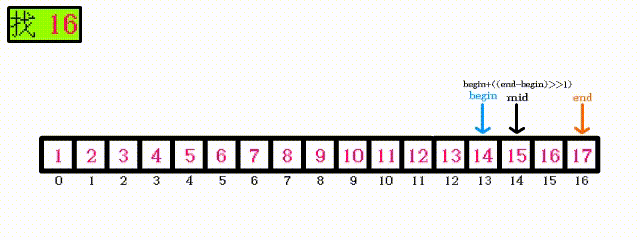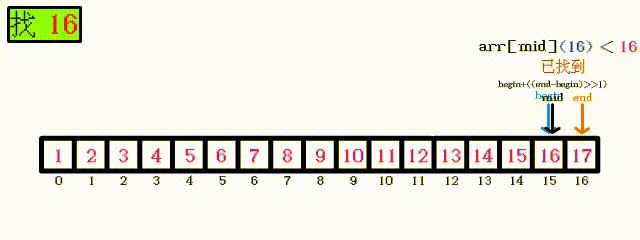
最坏的情况：

二分查找的原理：因为使用二分查找的数据必须是有序的，所以可以通过缩小查找范围来进行查找
二分查找每次查找一次，下一次查找的范围会缩小为当前范围的一半
只需要一张动图就可解释：

可以看出，每次查找之后，下一次需要查找的元素只剩下一半，所以最坏的情况其实是 需要查找：log N次
复杂度中，log N即为 以2为底N的对数

所以按照 大O 渐进表示法，取最坏的情况时间复杂度为 O(log N)

// 计算阶乘递归Fac的时间复杂度？  
long long Fac(size_t N)  
{  
	if(0 == N)  
		return 1;  

	return Fac(N-1)*N;  
}
1
2
3
4
5
6
7
8

此函数为 递归求阶乘
递归求阶乘，通过计算可以算出，求N的阶乘 则函数调用了 N次
所以按照 大O 渐进表示法，时间复杂度为 O(N)

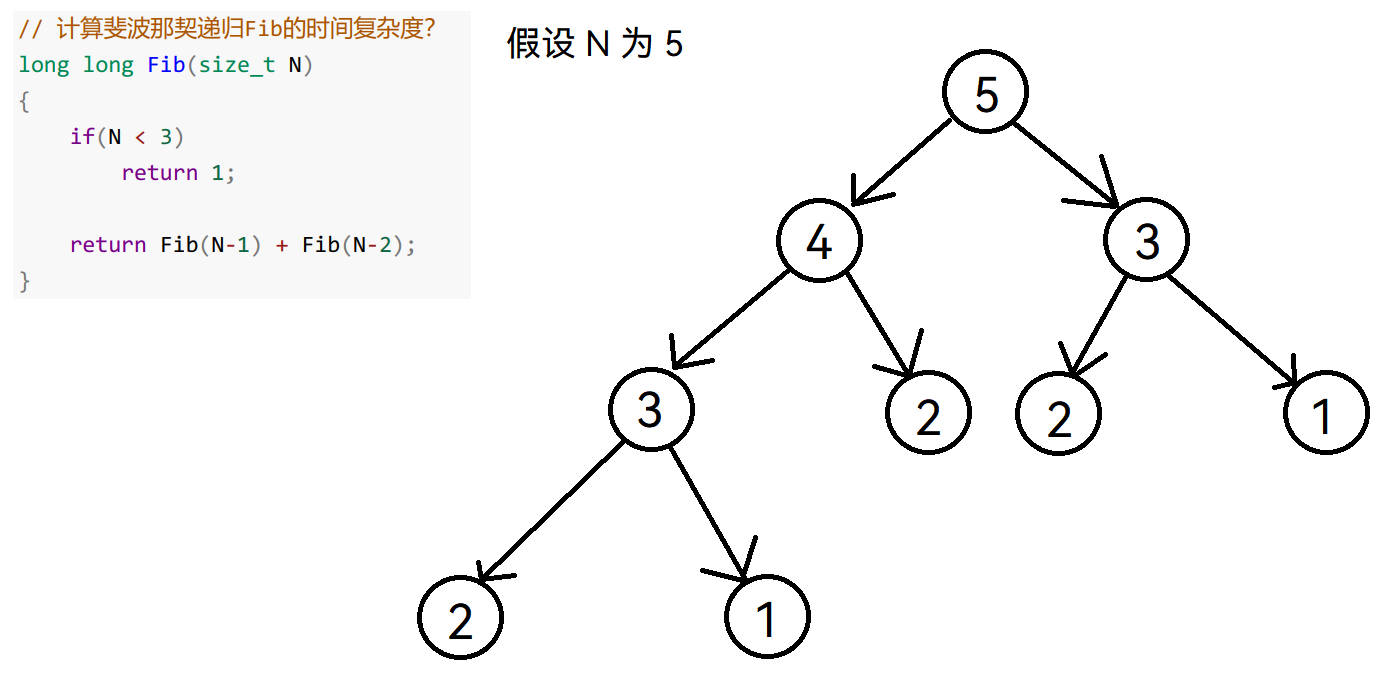
// 计算斐波那契递归Fib的时间复杂度
long long Fib(size_t N)  
{  
	if(N < 3)  
		return 1;  
		
	return Fib(N-1) + Fib(N-2);  
}
1
2
3
4
5
6
7
8

此函数为 递归求斐波那契数列
递归求斐波那契数列，一个简单的递归分析图：

发现正常调用函数，会再发生两次递归，所以应该是 2^N
但是因为当 N < 3 会返回 1，不再递归，所以应该是 2^N - x (不容易计算所以用 x 表示)，但是无论怎样，相减的常数因该是对2^N 造不成多大影响的
所以按照 大O 渐进表示法，时间复杂度为 O(2^N)

---

练习结束，感觉如何？？

空间复杂度

空间复杂度 主要衡量一个算法运行所需要的额外空间
这里提到一个词：额外空间

为什么是 额外空间 ？
因为，函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，在函数运行前就已经确定了一部分空间，这些空间的占用不能由算法本身决定
所以，空间复杂度主要通过 函数在运行时候申请的额外空间 来确定。

这里推荐一篇 详细又简单 的 函数栈帧 的好文章：
【程序员的自我修养】[动态图文] 超详解函数栈帧

在函数内使用动态开辟内存的函数，以及创建柔性数组等操作，就会增加函数的额外空间哦

空间复杂度 和 时间复杂度 的表示方法一样，都用 大O渐进表示法。

空间复杂度的计算举例

依然举几个例子：

// 计算BubbleSort的空间复杂度？  
void BubbleSort(int* a, int n)  
{  
	assert(a);  
	
	for (size_t end = n; end > 0; --end)  
	{  
		int exchange = 0;  
		for (size_t i = 1; i < end; ++i)  
		{  
			if (a[i-1] > a[i])  
			{  
				Swap(&a[i-1], &a[i]); 
				exchange = 1;  
			}  
		}  
		if (exchange == 0)  
			break;  
	}  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

分析代码可以看出，冒泡排序额外使用的空间并没有与 N 发生关联。使用了常量个额外空间
所以 按照 大O 渐进表示法，空间复杂度为 O(1)

// 计算Fibonacci的空间复杂度？  
// 返回斐波那契数列的前n项  
long long* Fibonacci(size_t n)  
{  
	if(n==0)  
		return NULL;  
	long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));  
	fibArray[0] = 0;  
	fibArray[1] = 1;  
	for (int i = 2; i <= n ; ++i)  
	{  
		fibArray[i] = fibArray[i - 1] + fibArray [i - 2];  
	}  
	
	return fibArray;  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

这是使用 数组实现的计算斐波那契数列的 前N 项
分析代码可以看出，这段代码 使用 malloc 函数开辟了 n+1 个 long long类型的空间，即额外使用的空间与 N 1:1相关
所以 按照 大O 渐进表示法，空间复杂度为 O(N)

// 计算阶乘递归Fac的空间复杂度？  
long long Fac(size_t N)  
{  
	if(N == 0)  
		return 1;  
		
	return Fac(N-1)*N;  
}
1
2
3
4
5
6
7
8

递归求N的阶乘
分析代码可以看出，代码执行需要递归 N 次，且每次递归都需要开辟函数栈帧，每次函数栈帧开辟都会消耗常量个空间，所以是 常量 * N
按照 大O 渐进表示法，空间复杂度为 O(N)

---

以上内容就是 关于 时间复杂度 和 空间复杂度 的介绍。
复杂度需要进行学习的已经介绍的差不多了。
但是，需要注意的是
其实大部分的代码，时间、空间复杂度是不容易直接看出来的，一定要执行分析。对存在循环体的代码，也不要直接简单粗暴的去数循环体执行的次数，因为循环并不一定是都需要执行的。一定要分析。

---

复杂度对比

常见的复杂度都有什么呢？

---

结束语

数据结构与算法关于复杂度的部分到这里就介绍完了。
本篇文章是对 数据结构与算法 这片神秘海域的初探索。
同样也是 向更深海域探索的重要基石

---

感谢阅读！

求三连！求三连！