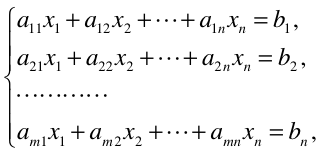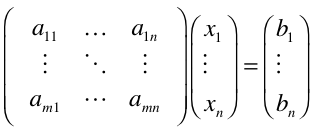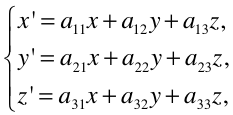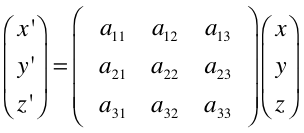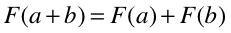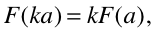热门标签
热门文章
- 19、yolov5s.yaml文件解读_yolov5 yolov5s6.yaml
- 2Linux 基础(七)常用命令 - 磁盘分区命令_linux磁盘分区命令
- 3C# 1.消息队列MQ使用场景--图文解析
- 4ChatGLM相关内容链接,供参考_chatglm官网
- 5Unity 百度SDK 之 在线语音合成 TTS WebAPI 功能的实现_unity 百度在线语音合成怎么使用
- 6Elasticsearch-集群架构详解
- 7TabNine代码补全工具使用体验
- 8Nature | 机器学习在药物研发中的应用_机器学习及自动化技术在医药研发领域的应用
- 9Pywinauto常用02--pywin32(Python调用win api)_pywin32怎么用
- 10(15)点云数据处理学习——单目深度估计获得RGBD图再重建点云_深度图像和rgb图像生成点云数据
当前位置: article > 正文
矩阵在图形学以及Unity中的应用_矩阵在图形学中的应用
作者:2023面试高手 | 2024-02-18 22:03:35
赞
踩
矩阵在图形学中的应用
自己整理了一下图形学中矩阵的相关内容,算是一个知识摘抄吧,正文如下。
1-矩阵简介
矩阵的定义是由若干行和若干列数排在一起组成的数表。
首先由线性方程组引出矩阵:
其中,方程组的全部系数,未知数,和等式右边的常数分别可以组成一个m*n,n*1,n*1的矩阵,那么上述方程组可以用矩阵的运算来表述为:
更多矩阵的数学方面基础知识在此不多做介绍,可以阅读参考文献2中线性代数的相关知识。
2-矩阵在坐标系转换中的应用
在3D图形学中,一个点的坐标或者一个平面的法向量都可以用一个3维向量来表示,所以在图形学中,可以用下面的线性变换方程组表示矩阵在坐标转换过程中的作用:
可以发现向量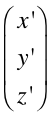
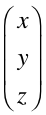
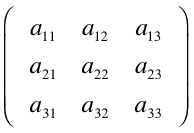
在图形学中,为了将一个顶点渲染到任意方向,任意位置的摄像机中,必须将物体的所有定点从物体坐标系变换到世界坐标系,接着再从世界坐标系变换到摄像机坐标系。其中的数学变换总结如下:
由上式可知,只要在渲染循环外将两个转换矩阵的乘积预先计算出来,就可以在渲染时通过一次转换完成从物体坐标到摄像机坐标的转换。
但是使用3*3矩阵转换坐标有一个问题,为了阐述这个问题先引入线性变换和仿射变换的概念。
在数学中,如果一个映射F保持了基本运算:加法和数量乘,那么就可以称该映射为线性的,即:
以及:
所以,上面对于向量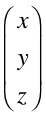
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/2023面试高手/article/detail/110852
推荐阅读
相关标签