计算机的运算基础_计算机运算

数制

基本知识

每一位的权由基数的幂次决定，不同位上的数有着不同的权值，这称为位权表示法，同时基数也代表着数码的个数。

特点为：

• 基数为$R$的数制中，包含$0,1,...,R-1$共$R$个数码
• 每个数字都要乘以基数的幂次，该幂次由每个数字所在的位置决定
• 小数点向右移动一位，数就扩大k倍；小数点向左移动一位，数就缩小k倍
• 每个数码只能有一个符号，多个符号就含有进位关系

对于任意一个k进制数A：$$\begin{gathered} A=A_n{A}_{n-1}...A_1{A}_0.A_{-1}{A}_{-2}...A_{-m}（并列表示法） \\ =A_n\times k^n+A_{n-1}\times k^{n-1}+...+A_1\times k^1+A_0\times k^0+A_{-1}\times k^{-1}+...+A_{-m}\times k^{-m}（多项式表示法） \\ =\sum _{i=n}^{-m}{A}_i\times k^i \end{gathered}$$

基于此的二（可以是k）进制转化为十进制程序：

#include <iostream>
#include <cmath>
using namespace std;

int main()
{
    char num[30];
    scanf("%s", num);
    int n, m = 0, flag = 0, len = (int)strlen(num);
    for (int i = 0; i < len; i ++)
    {
        if (flag) m ++;
        if (num[i] == '.') flag = 1;
    }    
    if (flag) n = len - m - 2;//字符串中含小数点
    else n = len - m - 1;//不含小数点
    // m为小数部分的位数，n为整数部分的位数-1
    double ans = 0;
    for (int i = 0, j = n; i < len; i ++)
    {
        if (num[i] == '.') continue; //跳过小数点 
        ans += (num[i] - '0') * pow(2, j);
        j --;
    }
    cout << ans;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

常见进制

• 十进制 —— decimal system
• 二进制 —— binary system
• 八进制 —— octal system
• 十六进制 —— hexadecimal system

十六进制中的特殊数码：

二进制的加法、乘法

十进制转化为k进制数

注意到：十进制小数并不是都能够用有限位的其它进制数精确地表示，这时应根据精度要求转换到一定的位数为止。
要求精度为$10^{-k}$时，设二进制小数位数为$m$，有：$2^{-m}\le 10^{-k}⟹m\ge \frac{k}{\lg 2}\approx 3.32k$，根据这种方法可以很方便的求出转换后的二进制小数的位数。
一般当要求二进制数取$m$位小数时，可求出$m+1$位，然后对最低位做0舍1入处理。

如果一个十进制数既有整数部分又有小数部分，则应将整数部分和小数部分分别进行转化，再把两者结果相加。

特殊技巧：
一个数除以$2^n$，就是将该数的二进制表示中的小数点左移$n$位。
例如 $13$（8+4+1）的二进制形式为：1101，因此$\frac{13}{16}$的二进制表示为：0.1101。

一个数乘以$2^n$，就是将该数的二进制表示中的小数点右移$n$位。

二进制、八进制、十六进制之间的转换

3位二进制数是1位八进制数，因此将二进制数转换为八进制数的方法为：

• 以小数点为界
• 将小数点左侧（整数部分）从右往左分别按每3位为1组，不足3位用0补足，转为8进制
• 将小数点右侧（小数部分）从左往右分别按每3位为1组，不足3位用0补足，转为8进制

八进制转换为二进制，只需将每一位转换为对应的二进制数即可。

4位二进制数是1位十六进制数，则转换方法类似于二进制、八进制之间的转换。

计算机中数的存储

码制

将带‘$\pm$’的二进制数称为真值；将符号和数值一起编码的二进制数称为机器码。例如：-1010就是真值，其对应的8位补码为1000 0110就是机器码。

$n$位二进制数的范围为：$[0,2^n)$

机器数有原码（signed magnitude number）、反码（diminished radix complement）、补码（radix complement）三种。

原码

原码是最简单的机器码，就是将真值中的符号转化为0或1而已，即：$$原码：符号位+真值绝对值$$严格的数学定义为：

• 整数的原码 [ X ] 原 = { X 0 ≤ X < 2 n 2 n − X − 2 n < X ≤ 0 [X]_原=\left\{

  $$\begin{matrix} X & 0\le X<2^n\\ 2^n-X&-2^n<X\le 0 \end{matrix}$$ \right. [X]原​={X2n−X​0≤X<2n−2n<X≤0​
  
  整数0的原码有00...0和10...0两种。
  在计算机中，每个数的表示都有位数限制。若一个整数用$n$位来存储，由于最高位被设置为符号位，因此$n$位原码的表示范围为：$-(2^{n-1}-1)\sim 2^{n-1}-1$。

• 小数（$\in (-1,1)$）的原码 [ X ] 原 = { X 0 ≤ X < 1 1 − X − 1 < X ≤ 0 [X]_原=\left\{

  $$\begin{matrix} X & 0\le X<1\\ 1-X&-1<X\le 0 \end{matrix}$$ \right. [X]原​={X1−X​0≤X<1−1<X≤0​
  
  小数0的原码有0.0...0和1.0...0两种。

反码

• 符号位与原码相同
• 数值位与符号相关。正数的反码与原码相同；负数反码的数值部分由原码的数值部分逐位取反得到。

严格的数学定义为：

• 整数的反码$$[X{]}_{反}=\{\begin{array}{cc}X& 0\le X<2^n\\ 2^{n+1}-1+X& -2^n<X\le 0\end{array}$$整数0的反码有00...0和11...1两种。

$n$位反码的表示范围与原码相同：$-(2^{n-1}-1)\sim 2^{n-1}-1$

• 小数的反码$$[X{]}_{反}=\{\begin{array}{cc}X& 0\le X<1\\ 2-2^{-n}+X& -1<X\le 0\end{array}$$小数0的反码有0.00...0和1.11...1两种。
  

补码

正数的补码和原码相同；负数的补码即反码+1。

严格的数学定义：

• 整数的补码 [ X ] 补 = { X 0 ≤ X < 2 n 2 n + 1 + X − 2 n < X ≤ 0 [X]_补=\left\{

  $$\begin{matrix} X & 0\le X<2^n\\ 2^{n+1}+X&-2^n<X\le 0 \end{matrix}$$ \right. [X]补​={X2n+1+X​0≤X<2n−2n<X≤0​整数0的补码只有一种：00...0，因此补码的表示范围要比原码、反码多1。
  -1的补码为：111...，$-2^{n-1}$的补码为：1000...。
  $n$位补码的表示范围为：$-2^{n-1}\sim 2^{n-1}-1$。
  
  注意：有些数可能有补码表示，但不存在原码和反码表示。

• 小数的补码 [ X ] 补 = { X 0 ≤ X < 1 2 + X − 1 < X ≤ 0 [X]_补=\left\{

  $$\begin{matrix} X & 0\le X<1 \\ 2+X&-1<X\le 0 \end{matrix}$$ \right. [X]补​={X2+X​0≤X<1−1<X≤0​小数0的补码只有1种：0.0...0

总结：

计算机中广泛采用补码表示，少数机器采用原码进行存储和传输，计算时用补码表示。

基于码制的整数运算

十进制与二进制之间在代数结构上是等价的，但对于机器数，由于符号位的存在，运算会较为复杂，特别是减法运算。

• 使用原码进行两个正数的相加可以得到正确结果的原码，但当运算数中存在负数时（存在减法），直接计算的结果就会出现问题。
  
  
  显然使用原码进行运算将增加运算的复杂性。

为了让计算机底层设计更加简单，人们开始探索将符号位参与运算，并且采用只保留加法的方法。如此便引入了反码。

• 引入反码的意义在于：无论两数相加还是相减，均可以通过加法实现。$$\begin{gathered} [X_1+X_2{]}_{反}=[X_1{]}_{反}+[X_2{]}_{反} \\ [X_1-X_2{]}_{反}=[X_1{]}_{反}+[-X_2{]}_{反} \end{gathered}$$运算时，符号位和数值位一样进行运算。当符号位有进位产生时，应将溢出的进位加到运算结果的最低位，才能得到正确结果。（主要是0有两种反码表示的缘故）
  
• 为了简化运算，又引入了补码。利用补码进行加、减运算时，其加、减也均可以通过加法实现。$$\begin{gathered} [X_1+X_2{]}_{补}=[X_1{]}_{补}+[X_2{]}_{补} \\ [X_1-X_2{]}_{补}=[X_1{]}_{补}+[-X_2{]}_{补} \end{gathered}$$运算时，符号位和数值位一样参加运算。区别在于：补码中0只有一种表示，若符号位有进位产生，则应将溢出进位丢弃就能得到正确结果（这也恰好便于电路设计）。
  
  可见采用补码进行加、减运算最方便，因此计算机中整数以补码的形式存储。
  
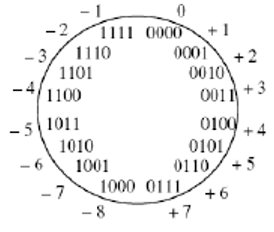
  补码表示法将所能表示的整数范围循环表示，因此要尤其注意整型数溢出的bug。
  

例如：将钟从11点调到3点，可以顺时针调4个小时，也可以逆时针调8个小时。

数的定点表示与浮点表示

定点表示法

即计算机中所有数的小数点位置是固定不变的，因此在计算机内部，小数点无需用专门的记号表示出来。如此表示的数叫做定点数。

• 定点小数表示法——小数点固定在符号位与最高位之间
  

• 定点整数表示法——小数点固定在数值位的最后
  

定点小数表示法表示的数都是绝对值小于1的纯小数，对于二进制$m+1$位的定点表示的数N，可以表示的范围为$|N|\le 1-2^{-m}$；
定点整数表示法表示的数都是绝对值在一定范围内的整数，对于二进制$m+1$位的定点表示的数N，可以表示的范围为$|N|\le 2^m-1$；
当超过这些范围时，为避免溢出，需要根据实际情况使用一个比例因子将所需存储的数缩小或放大，使用较为不便。

浮点数表示法

一个浮点数分为阶码（exponent）和尾数（mantissa）两部分：

阶码总是一个整数，正整数和负整数均可；尾数可以采用整数或纯小数两种形式。

通常情况下，在计算机内部，阶码采用 补码形式的整数 表示，尾数采用 原码形式的小数 表示，另外还有一个符号位。
浮点数的规格化形式：尾数的最高位必须是非零的有效位。

阶码和尾数所占用的位数可以灵活设定，由于阶码确定数的表示范围，尾数确定数的精度，所以字长一定时，分配给阶码的位数越多，表示的数的范围越大，但同时由于分配给尾数的位数减少，所以数的精度降低。

若阶码的位数为n，则阶码的范围为：$-2^{n-1}\sim 2^{n-1}-1$;若尾数的位数为m，则尾数的取值范围为：$2^{-1}\sim 1-2^{-m-1}$（尾数最高位必须非零）

对于32位字长（单精度float），通常采用的分配方式为：1位符号位、8位阶码、23位尾数。

此时，阶码的范围为：$-2^7\sim 2^7-1$，尾数的范围为：$2^{-1}\sim 1-2^{-24}$
则数值范围为：

当一个数超过浮点数的表示范围，将会发生溢出。
如果一个数的阶大于计算机所能表示的最大阶码，称为“上溢”，程序中断；如果一个数的阶小于计算机所能表示的最小阶码，称为“下溢”，该数视为0，仍可继续运算。