双目视觉（一）双目视觉系统

系列文章：

1. 双目视觉（一）双目视觉系统
2. 双目视觉（二）双目匹配的困难和评判标准
3. 双目视觉（三）立体匹配算法
4. 双目视觉（四）匹配代价
5. 双目视觉（五）立体匹配算法之动态规划全局匹配
6. 双目视觉（六）U-V视差
7. 双目视觉（七）稀疏双目匹配
8. 【项目实战】利用Ｕ-V视差进行地面检测
9. 【项目实践】U-V视差路面检测之动态规划

1.说说单目相机

在单目视觉中，是无法确定一个物体的真实大小，它可能很大很远，可能很近很小，例如上图中，P点和Q点为真实世界的3维点，但是它们在相机平面上都投影到了同一个点，这也就无法确定一个物体的真实尺寸，也就是所谓的失去了尺度信息。

说到这里，有些读者会问啦：为什么非得用双目相机才能得到深度？我闭上一只眼只用一只眼来观察，也能知道哪个物体离我近哪个离我远啊！是不是说明单目相机也可以获得深度？

在此解答一下：首先，确实人通过一只眼也可以获得一定的深度信息，不过这背后其实有一些容易忽略的因素在起作用：一是因为人本身对所处的世界是非常了解的（先验知识），因而对日常物品的大小是有一个基本预判的（从小到大多年的视觉训练），根据近大远小的常识确实可以推断出图像中什么离我们远什么离我们近；二是人在单眼观察物体的时候其实人眼是晃动的，相当于一个移动的单目相机，这类似于运动恢复结构（Structure from Motion, SfM）的原理，移动的单目相机通过比较多帧差异确实可以得到深度信息。

但是实际上，相机毕竟不是人眼，它只会傻傻的按照人的操作拍照，不会学习和思考。下图从物理原理上展示了为什么单目相机不能测量深度值而双目可以的原因。我们看到红色线条上三个不同远近的黑色的点在下方相机上投影在同一个位置，因此单目相机无法分辨成的像到底是远的那个点还是近的那个点，但是它们在上方相机的投影却位于三个不同位置，因此通过两个相机的观察可以确定到底是哪一个点。

2.如何确定尺度呢？

由于仅通过单张图像无法获得像素的尺度信息，那么怎么办呢？办法是有的，我们可以通过获得不同视角的图像，然后通过三角测量（Triangulation）（或三角化） 的方法来估计地图点的深度。

表示成我们熟悉的针孔相机模型：

 在上图中，我们知道相机的内部参数（K1,K2），已知匹配的点对（x1，x2）,相机的位姿（R,T），求X。那么其实质就是：

具体的推导： 

1.通过针孔模型，我们知道单幅图像的投影方程，如果不了解相机模型，可以看这篇博客（针孔相机模型）：

2.多幅图像的投影方程组合在一起：

 3.将上面两式整理可以得到：

 3.最后采用最小二乘法求解X,Y,Z。

代码实现：

//************************************
// Description: 根据左右相机中像素坐标求解空间坐标
// Method:    uv2xyz
// Parameter: Point2f uvLeft
// Parameter: Point2f uvRight
// Returns:   cv::Point3f
//************************************
cv::Point3d uv2xyz(cv::Point2d uvLeft,cv::Point2d uvRight,cv::Mat mLeftP,cv::Mat mRightP)
{
    //     [u1]      [xw]                      [u2]      [xw]
    //zc1 *|v1| = Pl*[yw]                  zc2*|v2| = P2*[yw]
    //     [ 1]      [zw]                      [ 1]      [zw]
    //               [1 ]                                [1 ]
 
    //最小二乘法A矩阵
    cv::Mat A = cv::Mat(4,3,CV_64F);
    A.at<double>(0,0) = uvLeft.x * mLeftP.at<double>(2,0) - mLeftP.at<double>(0,0);
    A.at<double>(0,1) = uvLeft.x * mLeftP.at<double>(2,1) - mLeftP.at<double>(0,1);
    A.at<double>(0,2) = uvLeft.x * mLeftP.at<double>(2,2) - mLeftP.at<double>(0,2);
 
    A.at<double>(1,0) = uvLeft.y * mLeftP.at<double>(2,0) - mLeftP.at<double>(1,0);
    A.at<double>(1,1) = uvLeft.y * mLeftP.at<double>(2,1) - mLeftP.at<double>(1,1);
    A.at<double>(1,2) = uvLeft.y * mLeftP.at<double>(2,2) - mLeftP.at<double>(1,2);
 
    A.at<double>(2,0) = uvRight.x * mRightP.at<double>(2,0) - mRightP.at<double>(0,0);
    A.at<double>(2,1) = uvRight.x * mRightP.at<double>(2,1) - mRightP.at<double>(0,1);
    A.at<double>(2,2) = uvRight.x * mRightP.at<double>(2,2) - mRightP.at<double>(0,2);
 
    A.at<double>(3,0) = uvRight.y * mRightP.at<double>(2,0) - mRightP.at<double>(1,0);
    A.at<double>(3,1) = uvRight.y * mRightP.at<double>(2,1) - mRightP.at<double>(1,1);
    A.at<double>(3,2) = uvRight.y * mRightP.at<double>(2,2) - mRightP.at<double>(1,2);
 
    //最小二乘法B矩阵
    cv::Mat B = cv::Mat(4,1,CV_64F);
    B.at<double>(0,0) = mLeftP.at<double>(0,3) - uvLeft.x * mLeftP.at<double>(2,3);
    B.at<double>(1,0) = mLeftP.at<double>(1,3) - uvLeft.y * mLeftP.at<double>(2,3);
    B.at<double>(2,0) = mRightP.at<double>(0,3) - uvRight.x * mRightP.at<double>(2,3);
    B.at<double>(3,0) = mRightP.at<double>(1,3) - uvRight.y * mRightP.at<double>(2,3);
 
    cv::Mat XYZ = cv::Mat(3,1,CV_64F);
    //采用SVD最小二乘法求解XYZ
    cv::solve(A,B,XYZ,cv::DECOMP_SVD);
 
    //std::cout<<"空间坐标为 = "<<std::endl<<XYZ<<std::endl;
 
    //世界坐标系中坐标
    cv::Point3d world;
    world.x = XYZ.at<double>(0,0);
    world.y = XYZ.at<double>(1,0);
    world.z = XYZ.at<double>(2,0);
 
    return world;
}

3.双目相机

上面讲了如何获得深度信息，一个相机可以通过获得不同视角的图像，然后通过三角测量计算深度，那么我们也可以添加另外一个相机在不同的位置拍摄同一个点，这样就和同一个相机在不同视角获得多幅图像等价了。

 注：在左相机相机平面上的点，投影到右相机平面为一条直线，这也就是极线约束，本质上是点和线的映射关系。

如果能将左相机平面中的点，在右相机平面中找到其对应的点，我们就可以获得深度值，进一步计算出物体的3维点信息。

 我们知道了：两个相机可以同过三角测量获得三维信息，那么就直接这样计算了吗？其实也可以，不过为了简便，我们通常需要将两个相机平面矫正到同一水平上。因为在矫正后的双目相机，我们搜索对应的匹配点的搜索空间也从2维变成了1维。

首先来看看，未校正前的左右相机的两个平面，（左平面和右平面不在同一水平面上）

 再来看看，极线矫正之后的双目相机：两个相机平面位于同一水平面上。

接下来我们来计算深度。

对于矫正后的针孔相机模型（如下图），我们可以使用简单的相似三角形的原理，来计算其深度值。

 首先，对于第一个相机坐标。

接下来，对于第二个相机坐标系。 

•  这两个三角形如下：

• X可以表达为:

•  两个等式合并

•  深度Z:

• 首先，对于针孔相机模型，根据相似三角形原理可以得到如下：

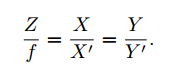
•  将上面的公式变换一下：

•  当然，现在X'和Y‘的坐标系是在图像的正中间，而我们处理的图像的坐标系，相对于在图像正中间的坐标系，原点平移了 [cx，cy]T，也放缩了一定的倍数。

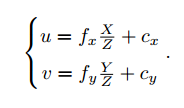
•  那么左相机的三维点X，Y就可以计算：

4.双目匹配

 现在已知双目相机的左图和右图，而且已知左图的点（红色）pl = (xl; yl),那么怎么在右图找到匹配点pr = (xr; yr)
呢？

step1:由于矫正后的双目相机的左图和右图的点，符合极线约束，即yr = yl，那么我们可以通过极线来缩减搜索区域。

 

 step2:在极线上我们如何去匹配，发现这个点是否是我们要找的点呢？

我们可以通过扫描极线，比较右图中的块和左图中的块，找到和左图最相似的那个就OK了。

 step3:如何判断哪个块最相似呢？

可以通过计算极线上的每个点匹配代价。

step4:得到匹配点后，通过匹配点的坐标得到视差d，然后根据视差值d，焦距f,j基线b,进一步计算深度值d

双目视觉系统：

参考：

https://www.cnblogs.com/zyly/p/9373991.html