2021年五一杯数学建模B题-消防救援问题_:依据附件2,请建立数学模型,分析该地各类事件密度与人口密度之间的关系(人口

2021年五一杯数学建模

B题 消防救援问题

原题再现：

  随着我国经济的高速发展，城市空间环境复杂性急剧上升，各种事故灾害频发，安全风险不断增大，消防救援队承担的任务也呈现多样化、复杂化的趋势。对于每一起出警事件，消防救援队都会对其进行详细的记录。
  某地有15个区域，分别用A、B、C…表示，各区域位置关系及距离如图1所示，各区域的人口及面积见附件1，该地消防救援队出警数据见附件2。
请依据该地的消防出警数据，建立数学模型，完成以下问题：
  问题1：将每天分为三个时间段（0:00-8:00为时段Ⅰ，8:00-16:00为时段Ⅱ，16:00-24:00为时段Ⅲ），每个时间段安排不少于5人值班。假设消防队每天有30人可安排值班，请根据附件数据，建立数学模型确定消防队在每年2月、5月、8月、11月中第一天的三个时间段各应安排多少人值班。
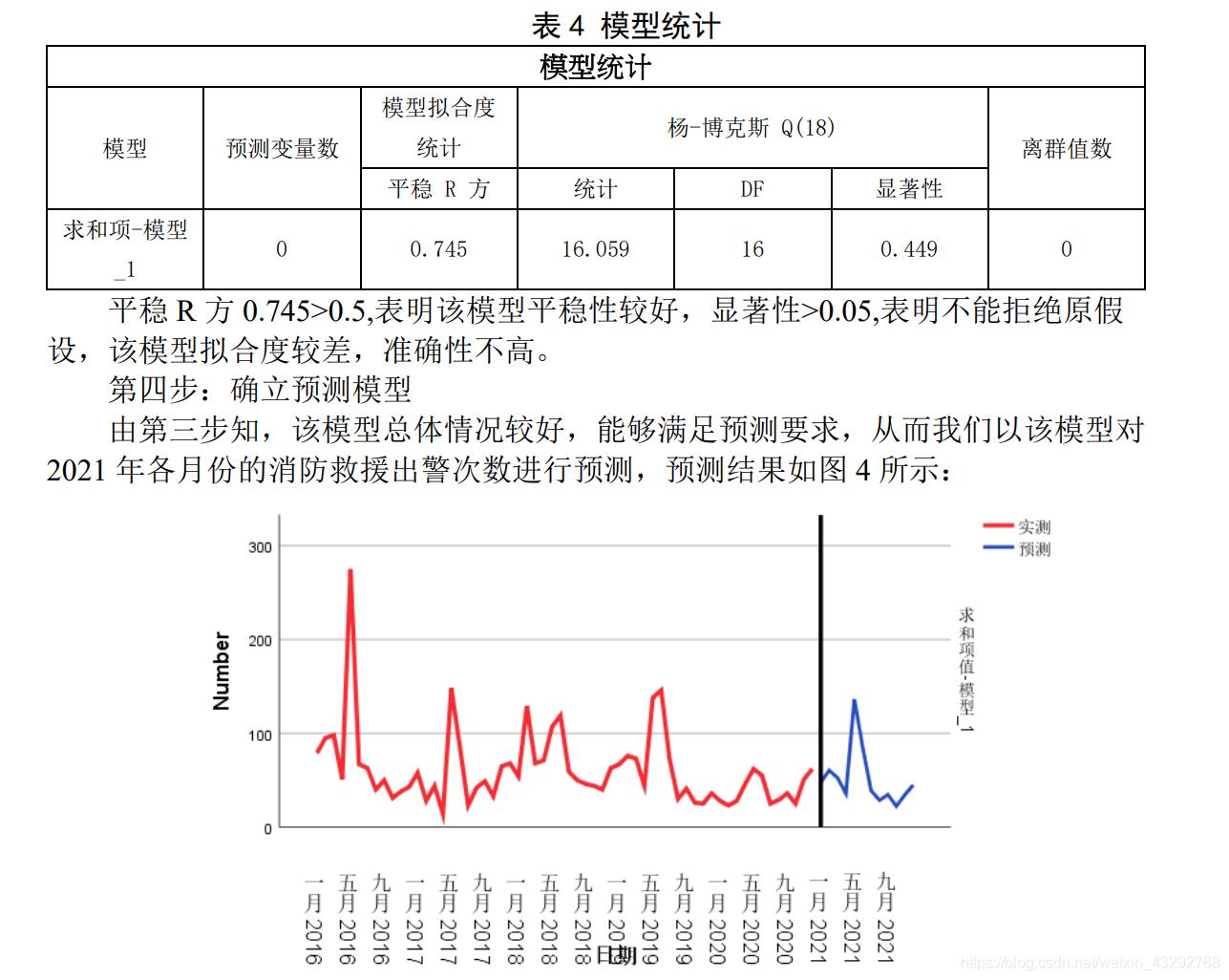
  问题2：以该地2016年1月1日至2019年12月31日的数据为基础，以月份为单位，建立消防救援出警次数的预测模型；以2020年1月1日至2020年12月31日的数据作为模型的验证数据集，评价模型的准确性和稳定性，并对2021年各月份的消防救援出警次数进行预测，完成表1。
  问题3：依据7种类别事件的发生时间，建立各类事件发生次数与月份关系的多种数学模型，以拟合度最优为评价标准，确定每类事件发生次数的最优模型。
  问题4：根据图1，请建立数学模型，分析该地区2016-2020年各类事件密度在空间上的相关性，并且给出不同区域相关性最强的事件类别（事件密度指每周每平方公里内的事件发生次数）。
  问题5：依据附件2，请建立数学模型，分析该地各类事件密度与人口密度之间的关系（人口密度指每平方公里内的人口数量）。
  问题6：目前该地有两个消防站，分别位于区域J和区域N，请依据附件1和附件2，综合考虑各种因素，建立数学模型，确定如果新建1个消防站，应该建在哪个区域？如果在2021-2029年每隔3年新建1个消防站，则应依次建在哪些区域？

整体求解过程概述(摘要)

  针对消防救援问题，本文研究了不同区域相关性最强的消防事件类别，以及分析了各类消防事件的密度与人口密度的关系，同时预测了每年 2 月、5 月、8 月、11月三个时间段对应的值班人数和 2021 年的各月份的消防救援出警次数，最后确定了新建消防站的区域。
  同时本文对消防人员都有准确的分配，对人员的分配是否科学，直接影响出警的效率、救援的高效性、对人员的公平分配，本文将建立相关的数学模型对其进行求解及其验证，为消防救援的一系列问题提供了一定的理论依据。
  针对问题 1，我们利用近五年出警次数的相关数据，统计出近五年的 2 月、5 月、8 月、11 月第一天的三个时间段的出警次数。由于样本容量较小，我们选用灰色预测模型对未来年份的同一时间段的出警次数进行预测。对于预测的出警次数采用规划模型对值班人数进行规划。
  针对问题 2，我们引入 ARIMA 预测模型，利用差分法对数据进行平稳性处理，使得模型更加稳定和准确，在对模型的检验中，发现该模型虽然拟合程度略差，但模型的平稳性较好，能够用于对 2021 年各月份的消防救援出警次数进行预测。
  针对问题 3，我们选用了插值拟合和 ARIMA 两种模型，建立各类事件发生次数与月份的关系，通过显著性检验发现插值拟合模型优于 ARIMA 模型。
  针对问题 4，我们首先绘制散点图判断出各类事件在空间上具有相关性，为了直观表示各指标在不同区域之间的相关性，采用皮尔逊系数进行直观展示，并给出了不同区域相关性最强的事件类别。
  针对问题 5，我们首先绘制散点图判断出人口密度与事件具有线性关系，由此可以采用灰色关联模型进行分析，结果发现二者关联程度较高，关联度均在 0.8 以上，其中③事件与人口密度的关联度最高。
  针对问题 6，选择消防站需要考虑的因素最多的就是平均出警距离，所以在本问题中我们选择出警距离作为建立消防站的唯一评判因素。利用 Dijkstra 算法计算各区域之间的最短距离，计算在区域 J 和区域 N 以外的 13 个区域新增一个消防站后的平均出警距离，取新增后平均出警距离最小的区域作为建消防站的区域。计算得新建的 1 个消防站应建立在 P 点，此后 9 年依次建立的区域为 P、D、F 点。

模型假设：

1. 假设附件中提供的数据真实可靠；
2. 假设出警情况没有其他特殊外界条件影响；
3. 假设所有的出警情况均在相同外界条件下进行；
4. 假设所有出警人员没有特殊情况的出现；
5. 假设出警速度不受外界环境影响；

问题分析：

  针对问题 1，关于确定人数值班问题，首先筛选并统计出 2020 年、2019 年、2018 年、2017 年、2016 年的 2 月、5 月、8 月、11 月的第一天的三个时间段的出警次数，通过灰色预测方法得到每年的这 2 月、5 月、8 月、11 月这四个月第一天的三个时间段出警次数的预测数据。在对三个时间段各分配 5 人的基础上，根据每个月第一天的三个时间段对应的权重比例对剩余 15 人进行合理分配，计算出人员分配的人数。
  针对问题 2，我们引入 ARIMA 预测模型，利用差分法对数据进行平稳性处理， 使得模型更加稳定和准确，对模型的检验我们采用平稳性 R 方与显著性检验。
  针对问题 3，我们选用了插值拟合和 ARIMA 两种模型，以此来建立各类事件发生次数与月份的关系。

  针对问题 4，我们首先绘制散点图判断出各类事件在空间上具有相关性，为了直观表示各指标在不同区域之间的相关性，采用皮尔逊系数进行直观展示。
  针对问题 5，我们首先绘制散点图判断出人口密度与事件具有线性关系，由此可以采用灰色关联模型进行分析。
  针对问题 6，选择消防站需要考虑的因素最多的就是平均出警距离，所以在本问题中我们选择出警距离作为建立消防站的唯一评判因素。利用 Dijkstra 算法计算各区域之间的最短距离，计算在区域 J 和区域 N 以外的 13 个区域新增一个消防站后的平均出警距离，取新增后平均出警距离最小的区域作为建消防站的区域。

模型的建立与求解：

  针对问题 3，确定每类事件发生次数的最优模型。第一步：建立模型先按照年份区分所有数据，观察发现数据基本无规律性，是属于随机事件。后决定采用插值与拟合和 ARIMA 预测模型，来建立各类事件发生次数与月份关系的数学模型 ，评价出拟合度最优的模型。
  1. 插值与拟合
  先求出 5 年数据相对应月份的均值，再分别对 7 类事件进行拟合，采用三次样条插值的方法，拟合效果如图 5 所示

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

部分程序如下:

load 'xx.mat' n=length(y); yy=ones(n,1);
yy(1)=y(1);
for i=2:n
yy(i)=yy(i-1)+y(i)
end
B=ones(n-1,2);
# 数据的计算逻辑
for i=1:(n-1)
B(i,1)=-(yy(i)+yy(i+1))/2; B(i,2)=1;
end BT=B'; for j=1:(n-1)
 
YN(j)=y(j+1);
end YN=YN';
A=inv(BT*B)*BT*YN; a=A(1);
u=A(2);
t=u/a;
t_test=input('输入需要预测的个数'); i=1:t_test+n;
yys(i+1)=(y(1)-t).*exp(-a.*i)+t; yys(1)=y(1);
for j=n+t_test:-1:2 ys(j)=yys(j)-yys(j-1);
end x=1:n;
xs=2:n+t_test; yn=ys(2:n+t_test);
plot(x,y,'^r',xs,yn,'*-b'); det=0;
for i=2:n
det=det+abs(yn(i)-y(i));
end det=det/(n-1);
disp(['百分绝对误差为：',num2str(det),'%']);
disp(['预测值为：',num2str(ys(n+1:n+t_test))]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

第三问：

load('data_of_202151B.mat')

PolicyTimes=[]; for i=2016:2020
for j=1:12

index =intersect(find(Year==i),find(Month==j)); PolicyTimes=[PolicyTimes;i,j,length(index)];
end
end
%% 绘制图像
for i=2016:2020
plot(PolicyTimes(PolicyTimes(:,1)==i,2),PolicyTimes(PolicyTimes(:,1)==i,3),'line width',3)
hold on grid on end
legend('2016','2017','2018','2019',& apos;2020','Location','Best');


s = 12;
x = PolicyTimes(1:48,3)'; n = 12;
m1 = length(x); for i = s+1:m1;
y(i-s) = x(i) - x(i-s);
end
w = diff(y);
m2 = 12;%length(2); k=0;
% for i = 0:5
%	for j = 0:5
%	if i == 0 & j == 0
%	continue
%	elseif i == 0
%	ToEstMd = arima('MALags',1:j,'Constant',0);
%	elseif j == 0
%	ToEstMd = arima('ARLags',1:i,'Constant',0);
%	else
 
%	ToEstMd = arima('ARLags',1:i,'MALags',1:j,' Constant',0);
%	end
%	k = k + 1;
%	R(k) = i;
%	M(k) = j;
%	[EstMd,EstParamCov,LogL,info] = estimate(ToEstMd,w');
%	numParams = sum(any(EstParamCov));
%	[aic(k),bic(k)] = aicbic(LogL,numParams,m2);
%	end
% end
% fprintf('R,M,AIC,BIC 的对应值如下\n%f');
% check = [R',M',aic',bic']

R=5; M=2;
ToEstMd = arima('ARLags',1:R,'MALags',1:M,'Consta nt',0);
[EstMd,EstParamCov,LogL,info] = estimate(ToEstMd,w'); w_Forecast =  forecast(EstMd,n,'Y0',w'); yhat = y(end) + cumsum(w_Forecast);
for j = 1:n
x(m1 + j) = yhat(j) + x(m1+j-s);
end

fprintf('2020 年各月份预测出警次数为'); x(m1+1:end)


hold on plot(1:12,x(m1+1:end),'linewidth',3) axis([1 12 0 280])
legend('2016','2017','2018','2019',& apos;2020','2020predict','Location','Best');

fprintf('各月份预测的准确性为');
Accuracy=(x(m1+1:end)-PolicyTimes(49:end,3)')./PolicyTimes(49:end,3)'


s2 = 12;
x2 = PolicyTimes(1:60,3)'; n2 = 12;
m_2 = length(x2); for i = s2+1:m_2;
 
y2(i-s2) = x2(i) - x2(i-s); end
w2 = diff(y2);


R2=5; M2=2;
ToEstMd2 = arima('ARLags',1:R2,'MALags',1:M2,'Con stant',0);
[EstMd2,EstParamCov2,LogL2,info2] = estimate(ToEstMd2,w2'); w_Forecast2 = forecast(EstMd2,n2,'Y0',w2');
yhat2 = y2(end) + cumsum(w_Forecast2); for j = 1:n2
x2(m_2 + j) = yhat2(j) + x2(m_2+j-s2);
end
fprintf('2021 年各月份预测出警次数为'); x2(m_2+1:end)

%% 绘制图像
hold on plot(1:12,x2(m_2+1:end),'linewidth',3)
legend('2016','2017','2018','2019',& apos;2020','2020predict','2021predict','Location ','Best'
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

第五问：

load('x.mat') x=x1;
for i=1:5
for j=1:9 x(i,j)=x(i,j)/x1(1,j) end
end x1=x
for i=1:5
for j=1:9 x(i,j)=abs(x(i,j)-x1(i,1)) end
end max=x(1,1) min=x(1,1) for i=1:5
for j=1:9 if x(i,j)>=max
max=x(i,j)
end
end end
for i=1:5
for j=1:9 if x(i,j)<=min
min=x(i,j)
end end
end
k=0.5 %分辨系数取值
l=(min+k*max)./(x+k*max)%求关联系数矩阵guanliandu=sum(l&apos;)/n [rs,rind]=sort(guanliandu,&apos;descend&apos;) %对关联度进行排序



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可