《机器学习》周志华课后习题答案——第三章 (1-7题)_试证明对于参数w,对率回归的目标函数

《机器学习》周志华课后习题答案——第三章 (1-7题)

一、试析在什么情形下式(3.2)中不必考虑偏置项b.

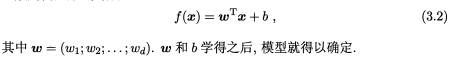
①b与输入毫无关系，如果没有b，y‘=wx必须经过原点
②当两个线性模型相减时，消除了b。可用训练集中每个样本都减去第一个样本，然后对新的样本做线性回归，不用考虑偏置项b。

二、试证明，对于参数w,对率回归的目标函数(3.18)是非凸的,但其对数似然函数(3.27)是凸的.

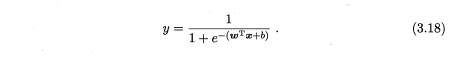
三、编程实现对率回归,并给出西瓜数据集3.0α上的结果.

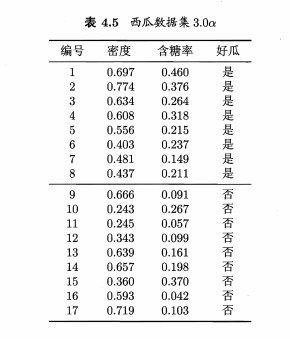
四、选择两个UCI数据集,比较10折交叉验证法和留–法所估计出的对率回归的错误率.

五、编程实现线性判别分析,并给出西瓜数据集3.0a上的结果.

六、线性判别分析仅在线性可分数据上能获得理想结果,试设计一个改进方法，使其能较好地用于非线性可分数据

在当前维度线性不可分，可以使用适当的映射方法，使其在更高维度上可分，典型的方法有KLDA，可以很好的用于非线性可分数据。

七、令码长为9,类别数为4,试给出海明距离意义下理论最优的ECOC二元码并证明之.

对于ECOC二元码，当码长为2^n时，知晓可以使2n个类别达到最优间隔，他们的海明距离为
2^（n-1），比如长度为8时，可以的序列为：

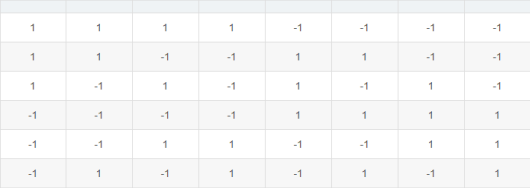
其中4，5，6行是对1，2，3行的取反。若分类数为4，一共可能的分类器，就是码长为9的最优分类器。