devbox
2023面试高手
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

无人驾驶LQR控制算法 c++ 实现_c++ lqr

作者：2023面试高手 | 2024-04-06 02:45:49

赞

踩

c++ lqr

参考博客：
（1）LQR的理解与运用 第一期——理解篇
（2）线性二次型调节器(LQR)原理详解
（3）LQR控制基本原理（包括Riccati方程具体推导过程）
（4）【基础】自动驾驶控制算法第五讲 连续方程的离散化与离散LQR原理

0 前言

LQR：线性二次调节器，设计状态反馈控制器的方法

1 LQR算法原理

系统： x ˙ = A x + B u \dot x=Ax+Bu x˙=Ax+Bu
线性反馈控制器： u = − K x u=-Kx u=−Kx
在这里插入图片描述
让系统稳定的条件是矩阵 A c l A_{cl} Acl​的特征值实部均为负数。因此我们可以手动选择几个满足上述条件的特征值，然后反解出K，从而得到控制器。

代价函数 J J J
在这里插入图片描述
在系统稳定的前提下，通过设计合适的K，让代价函数J最小。
Q大：希望状态变量x更快收敛
R大：希望输入量u收敛更快，以更小的代价实现系统稳定

1.1 连续时间LQR推导

具体推导参见博客：线性二次型调节器(LQR)原理详解

求解连续时间LQR反馈控制器参数K的过程：
（1）设计参数矩阵Q、R
（2）求解Riccati方程 A T P + P A − P B R − 1 B T P + Q = 0 A^TP+PA-PBR^{-1}B^TP+Q=0 ATP+PA−PBR−1BTP+Q=0得到P
（3）计算 K = R − 1 B T P K=R^{-1}B^TP K=R−1BTP得到反馈控制量 u = − k x u=-kx u=−kx

1.2 离散时间LQR推导

离散情况下的LQR推导有最小二乘法和动态规划算法
详细推导见博客：连续时间LQR和离散时间LQR笔记
离散系统：
x ( K + 1 ) = A x ( k ) + B u ( k ) x(K+1)=Ax(k)+Bu(k) x(K+1)=Ax(k)+Bu(k)
代价函数：
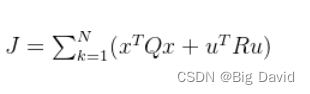
在这里插入图片描述
设计步骤：
① 确定迭代范围N
② 设置迭代初始值 P N = Q P_N=Q PN​=Q
③ t = N , . . . , 1 t=N,...,1 t=N,...,1，从后向前循环迭代求解离散时间的代数Riccati方程
P t − 1 = Q + A T P t A − A T P t B ( R + B T P t + 1 B ) − 1 B T P t A P_{t-1}=Q+A^TP_tA-A^TP_tB(R+B^TP_{t+1}B)^{-1}B^TP_tA Pt−1​=Q+ATPt​A−ATPt​B(R+BTPt+1​B)−1BTPt​A
④ t = 0 , . . . , N t=0,...,N t=0,...,N循环计算反馈系数 K t = ( R + B T P t + 1 B ) − 1 B T P t + 1 A K_t=(R+B^TP_{t+1}B)^{-1}B^TP_{t+1}A Kt​=(R+BTPt+1​B)−1BTPt+1​A 得到控制量 u t = − K t x t u_t=-K_tx_t ut​=−Kt​xt​

2 LQR代码

主要步骤：
（1）确定迭代范围N，预设精度EPS
（2）设置迭代初始值P = Qf，Qf = Q
（3）循环迭代， t = 1 , . . . , N t=1,...,N t=1,...,N
P n e w = Q + A T P A − A T P B ( R + B T P B ) − 1 B T P A P _{new} =Q+A ^TPA−A ^TPB(R+B ^T PB) ^{−1}B ^TPA Pnew​=Q+ATPA−ATPB(R+BTPB)−1BTPA
若 ∣ ∣ P n e w − P ∣ ∣ < E P S ||P_{new}-P||<EPS ∣∣Pnew​−P∣∣<EPS：跳出循环；否则： P = P n e w P=P_{new} P=Pnew​
（4）计算反馈系数 K = ( R + B T P n e w B ) − 1 B T P n e w A K=(R + B^TP_{new}B)^{-1}B^TP_{new}A K=(R+BTPnew​B)−1BTPnew​A
（5）最终的优化控制量 u ∗ = − K x u^*=-Kx u∗=−Kx

Reference_path.h

#pragma once

#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

#define PI 3.1415926

struct refTraj
{
    MatrixXd xref, dref;
    int ind;
};

struct parameters
{
    int L;
    int NX, NU, T;
    double dt;
};

class ReferencePath
{
public:
    ReferencePath();
    vector<double> calcTrackError(vector<double> robot_state);
    double normalizeAngle(double angle);

    // 计算参考轨迹点，统一化变量数组，便于后面MPC优化使用.
    refTraj calc_ref_trajectory(vector<double> robot_state, parameters param, double dl = 1.0);

public:
    vector<vector<double>> ref_path; // x, y, 切线方向, k
    vector<double> ref_x, ref_y;
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40

Reference_path.cpp

#include "Reference_path.h"

ReferencePath::ReferencePath()
{
    ref_path = vector<vector<double>>(1000, vector<double>(4));
    // 生成参考轨迹
    for (int i = 0; i < 1000; i++)
    {
        ref_path[i][0] = 0.1 * i;
        ref_path[i][1] = 2 * sin(ref_path[i][0] / 3.0);

        ref_x.push_back(ref_path[i][0]);
        ref_y.push_back(ref_path[i][1]);
    }
    double dx, dy, ddx, ddy;
    for (int i = 0; i < ref_path.size(); i++)
    {
        if (i == 0) {
            dx = ref_path[i + 1][0] - ref_path[i][0];
            dy = ref_path[i + 1][1] - ref_path[i][1];
            ddx = ref_path[2][0] + ref_path[0][0] - 2 * ref_path[1][0];
            ddy = ref_path[2][1] + ref_path[0][1] - 2 * ref_path[1][1];
        } else if (i == ref_path.size() - 1) {
            dx = ref_path[i][0] - ref_path[i- 1][0];
            dy = ref_path[i][1] - ref_path[i- 1][1];
            ddx = ref_path[i][0] + ref_path[i- 2][0] - 2 * ref_path[i - 1][0];
            ddy = ref_path[i][1] + ref_path[i - 2][1] - 2 * ref_path[i - 1][1];
        } else {
            dx = ref_path[i + 1][0] - ref_path[i][0];
            dy = ref_path[i + 1][1] - ref_path[i][1];
            ddx = ref_path[i + 1][0] + ref_path[i - 1][0] - 2 * ref_path[i][0];
            ddy = ref_path[i + 1][1] + ref_path[i - 1][1] - 2 * ref_path[i][1];
        }
        ref_path[i][2] = atan2(dy, dx);
        //计算曲率:设曲线r(t) =(x(t),y(t)),则曲率k=(x'y" - x"y')/((x')^2 + (y')^2)^(3/2).
        ref_path[i][3] = (ddy * dx - ddx * dy) / pow((dx * dx + dy * dy), 3.0 / 2); // k计算
    }
}
// 计算跟踪误差
vector<double> ReferencePath::calcTrackError(vector<double> robot_state)
{
    double x = robot_state[0], y = robot_state[1];
    vector<double> d_x(ref_path.size()), d_y(ref_path.size()), d(ref_path.size());
    for (int i = 0; i < ref_path.size(); i++)
    {
        d_x[i]=ref_path[i][0]-x;
        d_y[i]=ref_path[i][1]-y;
        d[i] = sqrt(d_x[i]*d_x[i]+d_y[i]*d_y[i]);
    }
    double min_index = min_element(d.begin(), d.end()) - d.begin();
    double yaw = ref_path[min_index][2];
    double k = ref_path[min_index][3];
    double angle = normalizeAngle(yaw - atan2(d_y[min_index], d_x[min_index]));
    double error = d[min_index];
    if (angle < 0) error *= -1;
    return {error, k, yaw, min_index};
}

double ReferencePath::normalizeAngle(double angle)
{
    while (angle > PI)
    {
        angle -= 2 * PI;
    }
    while (angle < -PI)
    {
        angle += 2 * PI;
    }
    return angle;
}

// 计算参考轨迹点，统一化变量数组，只针对MPC优化使用
// robot_state 车辆的状态(x,y,yaw,v)
refTraj ReferencePath::calc_ref_trajectory(vector<double> robot_state, parameters param, double dl)
{
    vector<double> track_error = calcTrackError(robot_state);
    double e = track_error[0], k = track_error[1], ref_yaw = track_error[2], ind = track_error[3];
    refTraj ref_traj;
    ref_traj.xref = MatrixXd(param.NX, param.T + 1);
    ref_traj.dref = MatrixXd (param.NU,param.T);
    int ncourse = ref_path.size();
    ref_traj.xref(0,0)=ref_path[ind][0];
    ref_traj.xref(1,0)=ref_path[ind][1];
    ref_traj.xref(2,0)=ref_path[ind][2];
    //参考控制量[v,delta]
    double ref_delta = atan2(k * param.L, 1);
    for(int i=0;i<param.T;i++){
        ref_traj.dref(0,i)=robot_state[3];
        ref_traj.dref(1,i)=ref_delta;
    }
    double travel = 0.0;
    for(int i = 0; i < param.T + 1; i++){
        travel += abs(robot_state[3]) * param.dt;

        double dind = (int)round(travel / dl);

        if(ind + dind < ncourse){
            ref_traj.xref(0,i)=ref_path[ind + dind][0];
            ref_traj.xref(1,i)=ref_path[ind + dind][1];
            ref_traj.xref(2,i)=ref_path[ind + dind][2];
        }else{
            ref_traj.xref(0,i)=ref_path[ncourse-1][0];
            ref_traj.xref(1,i)=ref_path[ncourse-1][1];
            ref_traj.xref(2,i)=ref_path[ncourse-1][2];
        }
    }
    return ref_traj;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108

LQR.h

#pragma once

#define EPS 1.0e-4
#include <Eigen/Dense>
#include <vector>
#include <iostream>
using namespace std;
using namespace Eigen;

class LQR {
private:
    int N;
public:
    LQR(int n);

    MatrixXd calRicatti(MatrixXd A, MatrixXd B, MatrixXd Q, MatrixXd R);
    double LQRControl(vector<double> robot_state, vector<vector<double>> ref_path, double s0, MatrixXd A, MatrixXd B, MatrixXd Q, MatrixXd R);
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18

LQR.cpp

#include "LQR.h"

LQR::LQR(int n) : N(n) {}
// 解代数里卡提方程
MatrixXd LQR::calRicatti(MatrixXd A, MatrixXd B, MatrixXd Q, MatrixXd R)
{
    MatrixXd Qf = Q;
    MatrixXd P_old = Qf;
    MatrixXd P_new;
    // P _{new} =Q+A ^TPA−A ^TPB(R+B ^T PB) ^{−1}B ^TPA
    for (int i = 0; i < N; i++)
    {
        P_new = Q + A.transpose() * P_old * A - A.transpose() * P_old * B * (R + B.transpose() * P_old * B).inverse() * B.transpose() * P_old * A;
        if ((P_new - P_old).maxCoeff() < EPS && (P_old - P_new).maxCoeff() < EPS) break;
        P_old = P_new;
    }
    return P_new;
}

double LQR::LQRControl(vector<double> robot_state, vector<vector<double>> ref_path, double s0, MatrixXd A, MatrixXd B, MatrixXd Q, MatrixXd R)
{
    MatrixXd X(3, 1);
    X << robot_state[0] - ref_path[s0][0],
         robot_state[1] - ref_path[s0][1],
         robot_state[2] - ref_path[s0][2];
    MatrixXd P = calRicatti(A, B, Q, R);
    // K=(R + B^TP_{new}B)^{-1}B^TP_{new}A
    MatrixXd K = (R + B.transpose() * P * B).inverse() * B.transpose() * P * A;
    MatrixXd u = -K * X; // [v - ref_v, delta - ref_delta]
    return u(1, 0);
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31

main.cpp

#include "LQR.h"
#include "KinematicModel.h"
#include "matplotlibcpp.h"
#include "Reference_path.h"
#include "pid_controller.h"

namespace plt = matplotlibcpp;

int main()
{
    int N = 500; // 迭代范围
    double Target_speed = 7.2 / 3.6;
    MatrixXd Q(3,3);
    Q << 3,0,0,
         0,3,0,
         0,0,3;
    MatrixXd R(2,2);
    R << 2.0,0.0,
         0.0,2.0;
    //保存机器人（小车）运动过程中的轨迹
    vector<double> x_, y_;
    ReferencePath referencePath;
    KinematicModel model(0, 1.0, 0, 0, 2.2, 0.1);
    PID_controller PID(3, 0.001, 30, Target_speed, 15.0 / 3.6, 0.0);
    LQR lqr(N);
    vector<double> robot_state;

    for (int i = 0; i < 700; i++)
    {
        plt::clf();
        robot_state = model.getState();
        vector<double> one_trial = referencePath.calcTrackError(robot_state);
        double k = one_trial[1], ref_yaw = one_trial[2], s0 = one_trial[3];

        double ref_delta = atan2(k * model.L, 1); // L = 2.2
        vector<MatrixXd> state_space = model.stateSpace(ref_delta, ref_yaw);

        double delta = lqr.LQRControl(robot_state, referencePath.ref_path, s0, state_space[0], state_space[1], Q, R);
        delta = delta + ref_delta;
        double a = PID.calOutput(model.v);
        model.updateState(a, delta);
        cout << "Speed: " << model.v << " m/s" << endl;

        x_.push_back(model.x);
        y_.push_back(model.y);
        //画参考轨迹
        plt::plot(referencePath.ref_x, referencePath.ref_y, "b--");
        plt::grid(true);
        plt::ylim(-5, 5);
        plt::plot(x_, y_, "r");
        plt::pause(0.01);
    }
    const char* filename = "./LQR.png";
    plt::save(filename);
    plt::show();
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57

CMakeList.txt

cmake_minimum_required(VERSION 3.0.2)
project(LQR)

## Compile as C++11, supported in ROS Kinetic and newer
# add_compile_options(-std=c++11)

## Find catkin macros and libraries
## if COMPONENTS list like find_package(catkin REQUIRED COMPONENTS xyz)
## is used, also find other catkin packages
find_package(catkin REQUIRED COMPONENTS
  roscpp
  std_msgs
)

set(CMAKE_CXX_STANDARD 11)

file(GLOB_RECURSE PYTHON2.7_LIB "/usr/lib/python2.7/config-x86_64-linux-gnu/*.so")
set(PYTHON2.7_INLCUDE_DIRS "/usr/include/python2.7")

catkin_package(
#  INCLUDE_DIRS include
#  LIBRARIES huatu
#  CATKIN_DEPENDS roscpp std_msgs
#  DEPENDS system_lib
)

include_directories(include
        ${PYTHON2.7_INLCUDE_DIRS}
)

add_executable(lqr_controller src/LQR.cpp
                              src/KinematicModel.cpp
                              src/main.cpp
                              src/pid_controller.cpp
                              src/Reference_path.cpp)
target_link_libraries(lqr_controller ${PYTHON2.7_LIB})

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36

3 PID vs Pure pursuit vs Stanley vs LQR

横向控制算法
（1）PID：鲁棒性较差，对路径无要求，转弯不会内切，速度增加会有一定超调，速度增加稳态误差变大，适用场景：路径曲率较小及低速的跟踪场景

（2）Pure pursuit：鲁棒性较好，对路径无要求，转弯内切速度增加变得严重，速度增加会有一定超调，速度增加稳态误差变大，适用场景：路径连续或不连续或者低速的跟踪场景

（3）Stanley：鲁棒性好，对路径要求曲率连续，转弯不会内切，速度增加会有一定超调，速度增加稳态误差变大，适用场景：路径平滑的中低速跟踪场景

（4）LQR：鲁棒性较差，对路径要求曲率连续，不会转弯内切，曲率快速变化时超调严重，稳态误差小，除非速度特别大，适用场景：路径平滑的中高速城市驾驶跟踪场景

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/2023面试高手/article/detail/369332
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号