热门标签
热门文章
- 1游戏包体大小优化 -- 实用篇_不简化代码会让包体变大吗
- 2LLM之RAG实战(三十二)| 使用RAGAs和LlamaIndex评估RAG
- 3jdk环境变量配置方法:
- 4AI架构师必知必会系列:强化学习
- 5oracle中asm磁盘不足,oracleasm磁盘管理基础篇(一)
- 6Hugging Face实战-系列教程10:文本预训练模型构建1(模型自动导入/transformers/BERT/模型蒸馏/文本截断处理/随机mask)、项目实战、源码解读_huggfacing教程bert
- 7陪诊系统:基于自然语言处理的患者沟通创新
- 8在 Vivado 中执行远程调试
- 9C++——优先级队列(priority_queue)的使用及实现_priorityqueue c++用法
- 10PyTorch数据结构
当前位置: article > 正文
八股文——机器学习基础损失函数
作者:2023面试高手 | 2024-04-06 23:07:42
赞
踩
八股文——机器学习基础损失函数
一、常见的代价函数
1、二次代价函数
J=1/2nΣ||a(x)-y(x)||^2
对于一个样本而言,J=(y-a)/2

激活函数的梯度越大,权值w和b大小调整的越快,训练收敛的越快
假使激活函数是sigmoid函数,当使用二次代价函数时,很可能会出现梯度消失,使用sigmoid函数在饱和区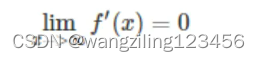 即x过大或者过小时,梯度是接近于0
即x过大或者过小时,梯度是接近于0
2.交叉熵代价函数
J=-1/nΣ[yln(a)+(1-y)ln(1-a)]
更适合搭配sigmoid激活函数
二、常见的损失函数
1.用于回归
绝对值损失函数和平方损失函数
绝对值损失函数MAE

平方损失函数MSE
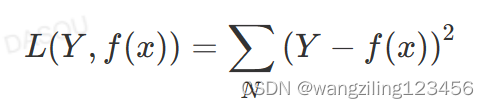
MSE比MAE可以更快的收敛,当使用梯度下降算法时,MSE梯度下降是变化的,MAE梯度损失是均匀不变的,梯度不发生改变不利于模型的训练(调节学习率)。
MAE鲁棒性更好,MAE与绝对损失之间是线性关系,MSE与误差是平方关系,当误差比较大时,MSE的误差更大。当数据中出现了一个非常大的离群点,MSE会产生非常大的损失,对模型的训练产生非常大的影响
2.用于分类
0-1损失函数
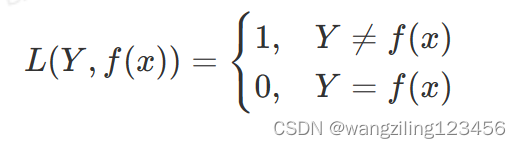
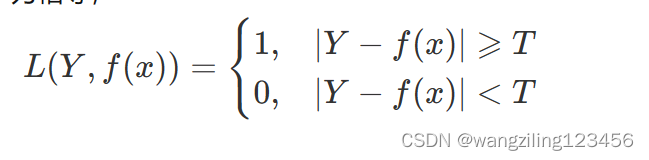
对数损失函数

指数损失函数
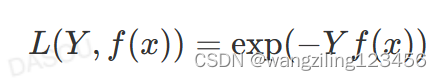
交叉熵损失函数
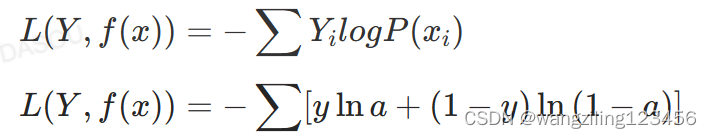
三、代价函数、损失函数、目标函数
目标函数:需要优化的函数=代价函数+结构风险(cost function+正则化)
损失函数是定义在单个样本上的,代价函数是定义在整个训练集上的,是所有样本误差的总和的平均
为什么回归问题中使用平方损失函数而不用交叉熵损失函数?
因为交叉熵损失函数在回归问题上只看到了正确的类别,而没有看到错误的另外。MSE是计算了全部的损失
为什么分类问题中使用交叉熵损失函数而不用平方损失函数
使用平方损失函数时,梯度下降与激活函数的导数成正比,sigmoid激活函数有饱和区,在饱和区内激活函数的导数趋近于0,会容易产生梯度消失的问题
使用交叉熵损失函数时,梯度下降与(激活函数-真实值)成正比,差值较大,更新就快,差值较小,更新就慢
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/2023面试高手/article/detail/374888
推荐阅读
相关标签


