各种排序算法比较

一、基本排序算法

1. 冒泡排序

    假如我们现在按身高升序排队，一种排队的方法是：从第一名开始，让两人相互比身高，若前者高则交换位置，更高的那个在与剩下的人比，这样一趟下来之后最高的人就站到了队尾。接着重复以上过程，直到最矮的人站在了队列首部。我们把队头看作水底，队尾看作水面，那么第一趟比较下来，最高的人就像泡泡一样从水底”冒“到水面，第二趟比较则是第二高的人……排队的过程即为对数据对象进行排序的过程（这里我们排序的”指标“是身高），上述过程即描述了冒泡排序的思想。从以上过程我们可以看到，若对n个人进行排队，我们需要n-1趟比较，而且第k趟比较需要进行n-k次比较。通过这些信息，我们能够很容易的算出冒泡排序的复杂的。首先，排序算法通常都以数据对象的两两比较作为”关键操作“，这里我们可以得出，冒泡排序需要进行的比较次数为: (n-1) + (n-2) + ... + 1 = n*(n-1) / 2，因此冒泡排序的时间复杂度为O(n^2)。

    理解了冒泡排序的原理，就不难实现它了，具体实现代码如下：

public class Bubble {
    public static void sort(int[] a) {
        int N = a.length;
        for (int i = 0; i < N - 1; i++)  {
            for (int j = 0; j < N - i - 1; j++) {
                if (a[j] > a[j+1]) {
                    exchange(a, j, j+1);
                }
            }
        }
    }

    public static void exchange(int a[], int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    public static void main(String[] args) {
        int N = 20;
        int[] a = new int[N];
        for (int i = 0; i < N; i++) {
            a[i] = StdRandom.uniform(0, 1000);
        }
        sort(a);
        for (Integer i : a) {
            StdOut.print(i + " ");
        }
    }
}

     关于冒泡排序有一点需要注意的是，在最好情况下（即输入数组已经完全有序），冒泡排序的时间复杂度能够提升到O(N)。我们只需增加一个boolean型变量isOrdered，在第一轮排序中一旦a[j] > a[j+1]，就把isOrdered设为false，否则isOrdered设为true，然后我们在每趟排序前检查isOrdered，一旦发现它为false，即认为排序已完成。

2. 选择排序

    回到上面我们提到的排队问题，除了上面提到的方法，还有这样一种排队的方法，让目前队头的人依次与其后的每个人进行比较，比较后较矮的那个人继续与后面的人进行比较，这样第一趟比较下来，就能够找到最矮的人， 然后把这个最矮的人和当前队头的人交换一下位置。然后第二趟比较，让第二名依次与后面比较，可以找到第二矮的人，然后让第二矮的人和当前队列第二名交换位置，依此类推，一共进行n-1趟比较后，就能完成整个排队过程。根据上述描述，我们可以知道，第k趟比较需要进行的数组元素的两两比较的次数为n-k次，所以共需要的比较次数为n*(n-1) / 2，因此选择排序算法的时间复杂度与冒泡排序一样，也为O(n^2)。选择排序的Java描述如下：

public class Selection {
     public static void sort(int[] a) {
         int N = a.length;
         for (int i = 0; i < N - 1; i++) {
             int min = i;
             for (int j = i + 1; j < N; j++) {
                 if (a[j] < a[min]) {
                     min = j;
                 }
             }
             exchange(a, i, min);
         }
     }

    public static void exchange(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

 }

3. 插入排序

   回想下我们平时打扑克抓牌的过程，通常我们用右手抓牌，每抓一张牌，就放到左手上，抓下一张牌后，会把这张牌依次与左手上的牌比较，并把它插入到一个合适的位置（通常按照牌面大小）。上述的过程即为插入排序的过程，假设待排序数组为a，我们从a[1]开始，让a[1]与a[0]比较，若a[1]较小，则让a[1]和a[0]交换位置，此时a[0]和a[1]就相当于已经放入左手中的牌。然后我们再让a[2]与a[1]、a[0]比较，并为它找到一个合适的位置，以此类推，直到为数组的最后一个元素也找到了合适的位置。

    理解了插入排序的思想后，我们便能够得到它的时间复杂度。对于n个元素，一共需要进行n-1轮比较，而第k轮比较需要进行k次数组元素的两两比较，因此共需要进行的比较次数为：1 + 2 + ... + (n-1)，所以插入排序的时间复杂度同冒泡排序一样，也为O(n^2)。插入排序的Java描述如下：

public class Insertion {
    public static void sort(int[] a) {
        int N = a.length;
        int i, j;
        for (i = 1; i < N; i++) {
            for (j = i - 1; j >= 0 && a[i] < a[j]; j--) {

            }
            //这里跳出内层循环，a[i]应被插入到a[j]后
            int tmp = a[i];
            for (int k = i; k > j + 1; k--) {
                a[k] = a[k-1];
            }
            a[j+1] = tmp;
        }
    }

}

    我们来简单地解释下以上代码。以抓牌过程来举例，i为刚抓的牌的索引，i-1即为我们刚排好的牌中的最后一张的索引，j为左手中当前正与我们刚抓的牌进行比较的牌的索引。在内层循环中，我们从左手已排好牌中的最后一张开始，若发现刚抓的牌比当前牌的牌面大，就再与前一张比较（j--），直到刚抓的牌大于等于当前牌的牌面，就会跳出内层循环，这时我们把a[i]插入到a[j]后，就把刚抓的牌插入到已排好牌中的合适的位置了。重复以上过程就能完成待排序数组的排序。

    关于插入排序我们需要注意的是，在平均情况下以及最坏情况下，它的时间复杂度均为O(n^2)，而在最好情况下（输入数组完全有序），插入排序的时间复杂度能够提升至O(N)。实际上，排序的本质就是消除逆序对，所谓逆序对，就是不符合我们所要求的排序顺序的两个数。比如说[1,3,4,2]为待排序数组，那么它的逆序数为2——(3,2)和(4,2)都是降序的，不符合我们升序的要求。插入排序对于部分有序的数组的排序尤为有效，所谓部分有序，指的是待排序数组的逆序数小于数组尺寸的某个倍数。若我们待排序数组完全有序时，每一轮排序都只需比较一次，就能找到待排序元素在已排序数组中的合适的位置，而部分有序时，比较的次数也能控制在数组尺寸的常数倍之内。因此，插入排序对于部分有序的数组十分高效，也很适合小规模的数组。

4. 希尔排序

    希尔排序是对插入排序的一种改进，它的核心思想是将待排序数组中任意间隔为h的元素都变为有序的，这样的数组叫做h有序数组。比如数组[5, 3, 2, 8, 6, 4, 7, 9, 5], 我们可以看到a[0]、a[3]、a[6]是有序的，a[1]、a[4]、a[7]是有序的，a[2]、a[5]、a[8]是有序的，因此这个数组是一个h有序数组（h=3）。根据h有序数组的定：义，我们可以知道，当h=1时，相应的h有序数组就是一个已经排序完毕的数组了。希尔排序的大致过程如下：把待排序数组分割为若干子序列（一个子序列中的元素在原数组中间隔为h，即中间隔了h-1个元素），然后对每个子序列分别进行插入排序。然后再逐渐减小h，重复以上过程，直至h变为足够小时，再对整体进行一次插入排序。由于h足够小时，待排序数组的逆序数已经很小，所以再进行一次希尔排序是很快的。希尔排序通常要比插入排序更加高效。

    实现希尔排序时，我们需要选取一个h的取值序列，这里我们直接采用算法（第4版） (豆瓣)一书中提供的h取值序列（1,4,13,40,121, ...)。即h =  3 * k + 1，其中k为[0, N/3)区间内的整数。希尔排序的Java描述如下：

public class Shell {
    public static void sort(int[] a) {
        int N = a.length;
        int h = 1;
        while (h < N / 3) {
            h = 3 * h + 1; //h的取值序列为1, 4, 13, 40, ...
        }
        while (h >= 1) {
            int n, i ,j, k;
            //分割后，产生n个子序列
            for (n = 0; n < h; n++) {
                //分别对每个子序列进行插入排序
                for (i = n + h; i < N; i += h) {
                    for (j = i - h; j >= 0 && a[i] < a[j]; j -= h) {

                    }
                    int tmp = a[i];
                    for (k = i; k > j + h; k -= h) {
                        a[k] = a[k-h];
                    }
                    a[j+h] = tmp;
                }
            }
            h = h / 3;
        }
    }

}

    实际上，h的取值序列的选取会影响到希尔排序的性能，不过以上我们选取的h值序列在通常情况下性能与复杂的取值序列相接近，但是在最坏情况下的性能要差一些。分析希尔排序的复杂度不是一件容易的事，这里我们引用《算法》一书中关于希尔排序复杂度的结论：

使用递增序列1, 4, 13, 40, 121, 364, ...的希尔排序所需的比较次数不会超过数组尺寸的若干倍乘以递增序列的长度。

    也就是说，在通常情况下，希尔排序的复杂度要比O(n^2)好得多。实际上，最坏情况下希尔排序所需要的比较次数与O(n^1.5)成正比，在实际使用中，希尔排序要比插入排序和选择排序、冒泡排序快得多。而且尽管待排序数组很大，希尔排序也不会比快速排序等高级算法慢很多。因此当需要解决排序问题而用没有现成系统排序函数可用时，可以优先考虑希尔排序，当希尔排序确实满足不了对性能的要求时，在考虑使用快速排序等算法。

    到这里，我们要介绍的基本排序算法就介绍完了，再介绍快速排序、归并排序、堆排序等高级排序算法前，我们先来简单地介绍下如何比较各种排序算法的实际性能，这也能够帮助我们直观的看到希尔排序相比与插入排序等的性能优势。

5. 比较不同排序算法的性能

   尽管插入排序和选择排序的复杂度都为O(n^2)，但是它们所包含的常数系数是不同的，因而这两种算法的实际执行时间之比应该是一个常数，下面我们来设计实验来测试下以上我们介绍的几种基本排序算法的实际执行性能。相关代码如下：

public class SortCompare {
    public static double time(String alg, int[] a) {
        long startTime = System.currentTimeMillis();
        if (alg.equals("Insertion")) {
            Insertion.sort(a);
        } else if (alg.equals("Selection")) {
            Selection.sort(a);
        } else if (alg.equals("Bubble")) {
            Bubble.sort(a);
        } else if (alg.equals("Shell")) {
            Shell.sort(a);
        }
        long endTime = System.currentTimeMillis();
        return (double) (endTime - startTime) / 1000.0;
    }

    public static double timeRandomInput(String alg, int N, int T) {
        //使用alg指定的排序算法将长度为N的数组排序，共排序T次，并计算总时间
        double total = 0.0;
        int[] a = new int[N];
        for (int t = 0; t < T; t++) {
            for (int i = 0; i < N; i++) {
                a[i] = StdRandom.uniform(10 * N);
            }
            total += time(alg, a);
        }
        return total;
    }

    public static void main(String[] args) {
        String alg1 = args[0];
        String alg2 = args[1];
        int N = Integer.parseInt(args[2]);
        int T = Integer.parseInt(args[3]);
        double t1 = timeRandomInput(alg1, N, T);
        double t2 = timeRandomInput(alg2, N, T);
        StdOut.printf("For %d random ints\n %s is", N, alg1);
        StdOut.printf(" %.1f times faster than %s", t2/t1, alg2);
    }
}

    我们来对1000个数进行排序，来比较下以上介绍的算法的性能。我这里得到的输出结果如下：

For 1000 random ints
 Shell is 4.9 times faster than Insertion

For 1000 random ints
 Shell is 7.6 times faster than Selection

For 1000 random ints
  Shell is 11.7 times faster than Bubble

   我们可以直观的看到，希尔排序要比其他三种排序都快，而插入排序要比选择排序、冒泡排序快，冒泡排序在实际执行性能最差。

   基本排序算法对于中小规模的数据集的排序在一般情况下足够用了，但是对于大规模数据集的排序，我们还是很有必要使用一些较高级的排序算法，下面我们来逐一介绍它们。

二、归并排序

    归并排序使用了一种叫做”分治“的思想来解决排序问题。分治也就是"分而治之“，也就是把一个大问题分解为众多子问题，而后分别得到每个子问题的解，最终以某种方式合并这些子问题的解就可以得到原问题的解。归并排序的主要思想是：将待排序数组递归的分解成两半，分别对它们进行排序，然后将结果“归并”（递归的合并）起来。我们知道，递归算法都有一个base case，递归分解数组的base case就是分解完的两个数组长度为为1，这时候它们本身就有序，此时就可以进行归并了。

    归并排序的时间复杂度为O(nlogn), 它的主要缺点是所需的额外空间与待排序数组的尺寸成正比。

1. 归并方法实现

    首先，我们先来实现归并方法，这个方法接收一个int[]数组a以及low、mid、high参数，用于将a[low..mid]（代表a[low]到a[mid]间的元素，包括a[low]和a[mid]）和a[mid+1..high]归并为一个数组，这个方法假设a[low..mid]与a[mid+1..high]都是有序的。

    下面我们用一个具体例子来描述归并算法的执行过程，假如我们的输入数组为[2, 4, 6, 8, 1, 3, 5, 7]，low为0，mid为3，high为7。我们称a[low..mid]为左数组，a[mid+1..high]为右数组，归并方法的执行过程如下：

• 取左右数组的第一个元素进行比较，较小的那个放入新数组的第一个位置中，如下图所示：

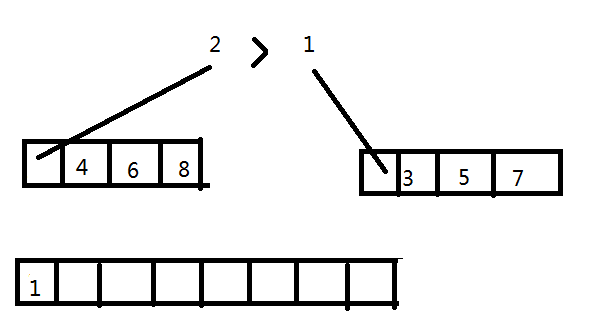
• 取右数组的下一个元素与2进行比较，较小的放入新数组的下一个位置，如下图所示：

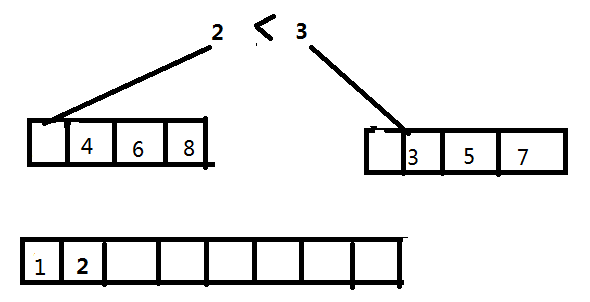
• 下一步我想不用我说大家也知道了，实际上我们可以把这个过程想象成左右两边轮番出人比武，比输的那个就被淘汰到“场外”，由于两边都是让弱的先出场，所以随后第一个出局的肯定就是最弱的。最后新数组中就按“武功高低”的升序对输入元素进行了排序。以上我们描述的就是归并方法的执行过程。

    理解了归并方法的原理，我们就不难用Java来描述它了，相关代码如下：

    private static void merge(int[] a, int low, int mid, int high) {
        int i = low; //左数组下一个要进行比较的元素的索引
        int j = mid + 1; //右数组下一个要进行比较的元素的索引
        int N = high + 1; //本次归并的元素数目
        int[] tmpArray = new int[N]; //用于暂时存放比较后的元素
        for (int k = low; k <= high; k++) {
            if (i > mid) {  //左数组元素已全比较完
                tmpArray[k] = a[j++];
            } else if (j > high) { //右数组元素已全比较完
                tmpArray[k] = a[i++];
            } else if (a[j] < a[i]) { //右数组元素小于左数组
                tmpArray[k] = a[j++];
            } else {  //右数组元素大于等于左数组
                tmpArray[k] = a[i++];
            }
        }
        for (int k = low; k < N; k++) {
            a[k] = tmpArray[k];
        }
    } 

    在以上代码中，我们使用了一个辅助数组tmpArray来暂时存放比较后的数组元素，待归并完成后，再复制回原数组。 

2. 自顶向下的归并排序

    上面我们介绍了归并过程的实现，归并方法要求输入数组的左半部分和右半部分分别有序。那么下面我们来介绍如何利用上面我们实现的merge方法来实现对一个数据集的归并排序。

    在最开始我们介绍过归并排序的主要思想是将待排序数组递归的分解成两半，分别对它们进行排序，然后将结果归并起来。具体过程如下：将数组递归的分为两部分，直至两部分长度都为1，则认为到达了base case，这时开始执行归并过程。

    这里我们还是以上面的输入数组举例，递归分解数组的示意图如下：

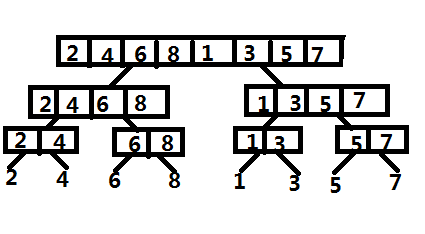
   我们可以看到，当数组分解为只有单个元素后，那么它就是有序的了，所以这时就满足了上面我们实现的归并方法的输入参数的条件，我们通过调用归并方法就能够以单元素数组为起点，逐步构造出已排序的完整数组。相关的实现代码如下：

public class Merge {
    private static void merge(int[] a, int low, int mid, int high) {
        ...
    }

    public static void sort(int[] a) {
        int N = a.length;
        sort(a, 0, N - 1);
    }

    private static void sort(int[] a, int low, int high) {
        //base case
        if (high <= low) {
            return;
        }
        int mid = (low + high) / 2;
        sort(a, low, mid);
        sort(a, mid+1, high);
        merge(a, low, mid, high);
    }

    public static void main(String[] args) {
        int N = 20;
        int a[] = new int[N];
        for (int i = 0; i < N; i++) {
            a[i] = StdRandom.uniform(1000);
        }
        sort(a);
        for (Integer i : a) {
            StdOut.print(i + " ");
        }
    }
}

     如果感觉以上代码比较抽象，大家可以画出“递归调用图”来帮助我们理解递归调用的过程，还是以上面的输入数组为例，我们画一下对它进行归并排序的递归调用图：

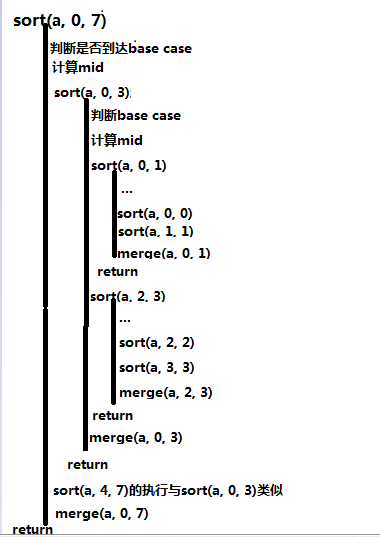
   通过这个图，我们可以直观地看到sort方法的递归调用过程。对于以上sort方法，以下几个方法能够提升它的性能：

• 对小规模子数组使用插入排序。
• 执行merge方法前，先判断下数组是否有序。这个方法能够大幅提升算法在最好情况（输入数组完全有序）的性能。

三、快速排序

    快速排序是目前应用最广泛的排序算法之一，它是一般场景中大规模数据排序的首选，它的实际性能要好于归并排序。通常情况下，快速排序的时间复杂度为O(nlogn)，但在最坏情况下它的时间复杂度会退化至O(n^2)，不过我们可以通过对输入数组进行“随机化”（打乱元素的排列顺序）来避免最坏情况的发生。除了实际执行性能好，快速排序的另一个优势是它能够实现“原地排序”，也就是说它几乎不需要额外的空间来辅助排序。下面我们来具体介绍下这个优秀排序算法的原理及实现。

1. 基本原理

    快速排序的主要思想如下：假设待排序数组为a[0..N-1]，递归的对该数组执行以下过程：选取一个切分元素，而后通过数组元素的交换将这个切分元素移动到位置j，使得所有a[0..j-1]的元素都小于等于a[j]，所有a[j+1..N-1]的元素都大于等于a[j]。

   在快速排序中，切分元素的选取很关键，通常我们可以选取输入数组的第一个元素作为切分元素，然后把它交换到数组中的合适位置使得它左边的元素都小于等于它，右边的元素都大于等于它，而后对其左右两边的子数组递归执行切分过程，即可完成对整个数组的排序。下面我们来看一下切分方法的Java描述，并以此来讲解切分过程的具体实现：

 1     private static int partition(int[] a, int low, int high) {
 2         int i = low + 1;
 3         int j = high + 1;
 4 
 5         //p为切分元素
 6         int p = a[low];
 7         while (true) {
 8             //从数组中的第二个元素开始寻找第一个大于等于切分元素的数组元素，若找到则i为其索引
 9             while (a[++i] < p) {
10                 if (i == high) {
11                     break;
12                 }
13             }
14             //此时i为从数组首部开始第一个大于等于切分元素的数组元素的索引，若没有找到则为high
15             
16             //从数组末元素开始寻找第一个小于等于切分元素的数组元素，若找到则j为其索引
17             while (a[--j] > p) {
18                 if (j == low) {
19                     break;
20                 }
21             }
22             //此时j为从数组末开始第一个小于等于切分元素的数组元素的索引，若没有找到则为low
23             
24             if (i >= j) {
25                 break;
26             }
27             exchange(a, i, j);
28         }
29         exchange(a, low, j);
30         return j;
31     }

    结合以上代码，我们来讲解一下确定切分过程的具体实现。首先在第6行中，我们选取了数组的首元素作为切分元素并将它保存在变量p中，然后在第7行进入一个无限循环中。

    第9行到第13行是一个内层循环，在这个循环中，我们从数组的第二个元素开始，让切分元素p与每个数组元素进行比较，当相应位置的元素大于等于p或是已经到达数组末尾时，这个循环就会终止。此时i的值为第一个大于等于p的元素的索引或是high的值，若为high的值则表示数组中不存在大于等于p的元素。

    然后我们来到了第17行到第21行的内层循环中，这个循环会从数组末元素开始，让p与数组元素逐一进行比较，当相应位置的元素小于等于p或是已比较到数组首时则终止循环。此时j的值为第一个小于等于p的元素的索引或是low的值，若为low的值则表示数组中不存在小于等于p的元素。

    接下来，执行第24行的if语句判断i和j的大小，若i >= j, 会跳出无限循环。i >= j对应着以下四种情况：

• 第一种情况：数组中存在大于等于p的元素，也存在小于等于p的元素，此时若i>=j说明第一个大于等于p的元素在第一个小于等于p的元素的右边（或是它俩本身是一个元素），我们来看下这种情况的图示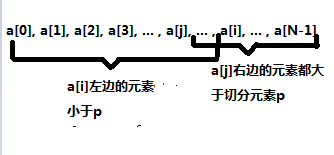：实际上， 左图中a[j]与a[i]间是不存在元素的，因为没有元素能同时满足大于p和小于p这两个条件。因此在这种情况下，实际上a[i]和a[j]是相邻的。所以这时候我们只需跳出无限循环，并交换a[low]和a[j]就能够完成切分；
• 第二种情况：数组中存在大于等于p的元素，而不存在小于等于p的元素，即此时i为第一个大于等于p的元素的索引，j为low，所以这时必然满足i > j。那么此时我们便已经完成了切分（a[j]右边的元素均大于p，左边没有元素），所以直接跳出无限循环，为统一上一种情况，我们也交换下low和j处的元素（虽然实际上就是自己和自交换）；
• 第三种情况：数组中不存在大于等于p的元素，存在小于等于p的元素，此时i为high，j为第一个小于等于p的元素的索引，因此此时i = j = high。所以此时也完成了切分（a[j]左边的元素均小于p，右边没有元素），所以这时候跳出无限循环并将low处和j处的元素呼唤，就完成了切分。
• 第四种情况：数组中既不存在大于等于p的元素，也不存在小于等于p的元素，这意味着数组中的所有元素都等于p。那么此时经过两个内层循环后，i的值为high，j的值为low。所以已经完成了切分，此时跳出无限循环后，为了与以上情况相统一，交换low与j处的元素（实际上是自己和自己交换）。

    下面我们再来看一下当i < j时我们应该怎么做。首先我们需要明确的是i < j意味着第一个大于等于p的元素(a[i])在第一个小于等于p的元素(a[j])的左边。如下图所示：

   那么现在问题来了，a[i]和a[j]之间的元素和p的关系是怎样的呢？答案是无法确定，所以当i<j时我们还不能贸然退出无限循环，得先把a[i]与a[j]之间的元素与p的大小关系确定了才行。不过现在的问题是出现了两只“拦路虎”——突然出现了a[i]这个大于等于p的元素拦着我们让我们无法继续向数组尾部寻找小于p的元素，而a[j]这个小于等于p的元素的出现使得我们无法向数组头部探索是否还有大于p的元素。那么解决方法来了，我们只要想办法移除这两个挡道的不就行啦。慢着...交换下a[i]和a[j]不就好了，这样我们就可以继续探索了呀，再遇到拦路虎的时候再交换它俩就可以了呀...以上代码第27行就完成了这个交换的工作。

   关于切分方法还有一点需要我们注意的是：在从左向右“扫描”时，必须在遇到大于等于切分元素p的元素时停下来，在从右向左扫描时，必须在遇到小于等于切分元素p的元素时停下来。若不是这样做的话，当数组有大量重复元素时，快速排序的时间复杂度就会退化至O(n^2)。

   现在，我们已经结合源代码，比较详细地阐述了切分过程的实现。下面，让我们借助这个切分过程，来实现用快速排序算法对一个数组进行排序。

2. 实现

   实际上，搞懂了上面的切分过程，来具体实现快速排序是很容易的，参考代码如下：

 1    public static void sort(int[] a) {
 2         StdRandom.shuffle(a); //打乱输入数组的元素间的相对顺序，避免出现最坏情况
 3         sort(a, 0, a.length - 1);
 4     }
 5 
 6     private static void sort(int[] a, int low, int high) {
 7         if (high <= low) {
 8             return;
 9         }
10         int j = partition(a, low, high);
11         sort(a, low, j-1);
12         sort(a, j+1, high);
13     }

    跟我们前面所描述的快速排序的基本思想一样，递归地对待排数组进行切分就能够完成排序。这里我们简单介绍下快速排序的性能特点。快速排序算法的实际执行性能依赖与切分是否均衡，当正好把数组从中间”切开”时，快速排序的实际性能最好。切分越不均衡快速排序的实际性能就越差，最坏情况下（第一次选取的切分元素是数组里最小的，第二次的切分元素是第二小的...），算法的时间复杂度会退化到O(n^2)。所以为了避免最坏情况的发生，我们在使用快速排序对数组排序时，会先打乱一下数组元素的顺序。一个好消息是在平均情况下，我们将数组打乱后再取第一个元素作为切分元素，切分通常是比较均衡的。

3. 对快速排序算法的改进

    尽管快速排序已经具有非常优秀的实际性能，但是仍然有许多行之有效的方法能够明显提升快速排序的速度，下面我们将简单地介绍以下这些方法。

（1）对于小数组使用插入排序

    对于尺寸比较小的数组，插入排序要比快速排序快，因此当递归调用切分方法到切分所得数组已经很小时，我们不妨用插入排序来排序小数组。只需要把以上快速排序实现代码的7—9行改为如下：

if (high <= low + SIZE) {  //SIZE为使用插入排序的临界数组尺寸，可以选取[5，15]上的整数
    Insertion.sort(a, low, high);
    return;
}

（2）三取样切分

    这项改进方案的手段是改进切分过程，具体方法如下：在每次切分时，从待切分数组中随即抽取3个元素，而后计算出它们3个元素的中位数来作为切分元素。也就是说，相比于上面我们实现的快速排序，三取样切分就是在切分元素的选取上有所不同。以下是三取样切分的实现：

public class Quick3d {
    public static void sort(int[] a) {
        sort(a, 0, a.length);
    }

    private static void sort(int[] a, int low, int high) {
        if (high <= low) {
            return;
        }
        int lt = low;
        int i = low + 1;
        int gt = high;
        int p = a[low];

        while (i <= gt) {
            if (a[i] < p) {
                exchange(a, i++, lt++);
            } else if (a[i] > p) {
                exchange(a, i++, gt--);
            } else {
                i++;
            }
        }
    }

    public static void exchange(int a[], int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

四、堆排序

1. 优先队列

   介绍堆排序之前，我们需要先介绍一种常用的数据结构——优先队列，因为堆排序就是基于优先队列实现的。优先队列可以分为最大优先队列和最小优先队列，最大优先队列主要支持两种操作：插入元素和删除最大元素，最小优先队列则支持插入元素和删除最小元素。在下面的介绍中，若未加特殊说明，我们所说的优先队列指的是最大优先队列。优先队列适用于如下这种场景：不需要对数据集完全有序，我们只需要获取数据集最大的一个或几个元素。优先队列可以基于数组实现，也可以基于二叉堆来实现，通常二叉堆都基于二叉堆来实现，所以这里我们主要介绍这种实现。

（1）几个概念

    在介绍基于二叉堆实现的优先队列前，我们先来介绍几个概念，这几个概念的定义均来自于Sedgewick的《算法》一书。第一个我们要介绍的概念堆有序，它的定义如下：

当一棵二叉树的每个结点都大于等于它的两个子结点时，它被称为堆有序。 

    第二个概念是二叉堆，它的定义如下：

二叉堆是一组能够用堆有序的完全二叉树排序的元素，并在数组中按照层级存储（不用数组的第一个位置）。

     我们来画张图说明一下堆有序的完全二叉树是怎样按照层级存储在数组中的：

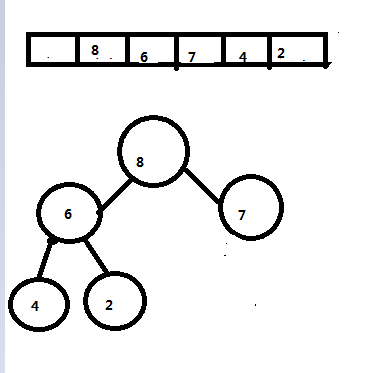
    从上图中我们可以看到二叉树中的元素是怎样和数组中对应的。使用这种顺序将二叉树元素存储在数组中所带来的一个最直接的好处就是很容易定位到一个数组元素a[k]在树中的父结点和两个子结点在数组的的位置：a[k]的父结点为a[k/2]，左子结点为a[2*k], 右子结点为a[2*k+1]。这种容易定位父子结点的性质加上下面的一个二叉堆的特性使得我们能够基于二叉堆高效的实现优先队列：一棵大小为N的完全二叉树的高度为floor(lgN)。（其中floor表示向下取整，lgN表示以2为底的N的对数）

（2）基于二叉堆实现的优先队列

    我们通过前面对二叉堆的定义可以知道，二叉堆可看做一棵堆有序的完全二叉树，所以二叉堆的各个元素间是有着一定的相对顺序的。具体说来，就是每个结点都大于等于它的两个子结点。所谓堆的有序化是指：当我们向二叉堆中添加一个元素或从二叉堆中删除一个元素后，导致二叉堆的有序性贝尔打破，这时我们要通过某种过程来恢复二叉堆的有序性，这个过程就是堆的有序化。（若未做特殊说明，以下提到的“堆”均指“二叉堆”）。

    堆的有序化可分为两种，一种是由下向上的有序化，通常叫做上浮（swim）；还有一种是由上向下的有序化，通常叫做下沉（sink）。它们的名字便很清楚了表明了它们各自的作用，上浮就是让一个结点向上移动到满足堆有序的位置，下沉就是让一个结点向下移动到满足堆有序的位置，下面我们来分别介绍它们。

a. 上浮过程的实现

    什么情况下我们需要上浮呢？通常是某个结点的值变大或是我们向堆中添加一个新结点时（它会被添加到数组尾部，也就是成为堆的叶子结点），我们需要把这个结点上浮到一个合适的位置以保证堆有序。根据堆有序的定义，当我们要进行上浮的结点大于它的父结点时，我们就需要把它不断的上浮，直到它小于等于它的父结点。参考代码如下：

    private void swim(int k) {
        while (k > 1 && a[k/2] < a[k]) {
            exchange(k, k/2 );
            k = k / 2;
        }
    }

b. 下沉过程的实现

    当某个结点的值比它的某个子结点更小时，我们需要把该结点下沉来保证堆的有序性。下沉操作的过程中，我们应当先比较被下沉结点的两个子结点的大小，而后让被下沉结点与较大的那个比较，若是小于它，则两者交换，而后重复这个过程直到父结点大于等于两个子结点或是到达末尾。参考代码如下：

    private void sink(int k) {
        while (2 * k <= N) {
            int j = 2 * k;
            if (j < N && a[2*k] < a[2*k+1]) {
                j++;
            }
            if (k >= j) {
                break;
            }
            exchange(k, j);
            k = j;
        }
    }

    了解了堆的有序化的过程，优先队列的insert方法以及delMax方法的实现就很容易了，下面我们来基于以上的swim和sink方法来介绍insert与delMax方法的具体实现。为简单起见，我们假设结点均为int型。

c. insert方法的实现

    有了上面的铺垫，实现insert方法就很简单了，我们只需要把新结点添加到数组a的尾部，然后把它上浮到合适的位置即可，具体实现代码如下：

    public void insert(int node) {
        a[++N] = node;
        swim(N);
    }

d. delMax方法的实现

    由于我们始终保持二叉堆处于有序状态，所以根结点就是最大的结点，我们可以删除根结点，然后把数组尾部结点放入根结点的位置，再把它进行下沉即可，参考代码如下：

    public int delMax(int k) {
        exchange(1, N);
        int max = a[N--];
        a[N+1] = -1;
        sink(1);
        return max;
    }

    现在我们已经成功实现了一种insert方法与delMax方法的复杂度均为O(logn)的优先队列。实际上我们上面实现的每次可以删除一个最大结点的优先队列叫做最大有限队列，与它相对的每次可以删除一个最小结点的优先队列就是最小优先队列。接下来让我们基于（最大）优先队列来实现堆排序。

2. 堆排序

    我们知道，每次调用优先队列的delMax方法都会删除一个最大的结点，其时间复杂度为O(logN)。那么对于一个大小为N的数据集，我们只需要将它包含的元素都添加到优先队列中，然后调用N次delMax不就可以实现排序了吗？实际上这种区别与之前我们所介绍的排序方法的排序实现就是堆排序，堆排序的时间复杂度为O(nlogn)。

    堆排序通常分为两个阶段，第一个阶段是堆的构造阶段，用于把我们输入的无序数组构造成二叉堆；第二个阶段是下沉排序阶段，这个阶段我们删除一个最大结点并下沉以保证堆有序。下面我们来具体介绍这两个阶段的实现。

（1）堆的构造阶段

    这个阶段我们的任务是把一个无序数组构造成一个二叉堆，要实现这一任务，我们可以从数组的尾部开始对每个元素调用sink方法，若一个结点的两个子结点都已经是堆，那么我们对该结点调用sink就可以将它们整合成一个堆。对于没有子结点的堆，我们无需对其调用sink方法。

（2）下沉排序阶段

    下沉排序的逻辑很简单，就是让最大结点（即根结点）与数组末尾对应的结点交换，这样就把最大结点移动到了数组末尾，然后把刚交换到根结点的结点进行sink，此时根结点即为第二大的结点，然后再将根结点与数组末尾对应的结点交换….这样重复N-1次就能实现数组的原地排序。

    结合以上两个阶段，就可以得到堆排序的完整实现：

public class Heap {
    private static void sink(int[] a, int k, int N) {
        while (2 * k <= N) {
            int j = 2 * k;
            if (j < N && a[j] < a[j+1]) {
                j++;
            }
            if (a[k] >= a[j]) {
                break;
            }
            exchange(a, k, j);
            k = j;
        }
    }

    public static void sort(int[] a) {
        int N = a.length - 1;
        for (int k = N/2; k >= 1; k--) {
            sink(a, k, N);
        }
        while (N > 1) {
            exchange(a, 1, N--);
            sink(a, 1, N);
        }
    }

    public static void exchange(int a[], int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

}

（3）堆排序算法的评价

    《算法》一书中对堆排序评价如下：

堆排序是我们所知的唯一能够同时最优地利用空间和时间的方法——在最坏情况下他也能保证~2NlgN次比较和恒定的额外空间。

    其中~2NlgN表示比较次数的增长量级为2NlgN。也就是说若设比较次数为f(N)，当N足够大时，f(N) / 2NlgN趋向于1。由于这个特性，堆排序算法适合于空间资源十分紧张的嵌入式系统。

    堆排序的一个主要缺点在于缓存不友好，因为它经常要对内存中不相邻的元素进行比较，所以缓存命中率要低于快速排序、归并排序等算法。

五、排序算法的总结

1. 稳定性

    在比较各个排序算法前，我们先来介绍以下稳定性这个重要的概念。它的定义如下：

如果一个排序算法能够保留数组中重复元素的相对位置则可以被称为是稳定的。

    这个性质在有些场景中是必要的，特别是我们要对数据集进行多轮排序时。比如我们要排序的是交易事务数据集，每个交易事务都有交易时间和交易金额等信息。我们第一轮先按照交易金额排序，然后我们想再对于这些交易事务按照交易时间排一次序。此时若排序算法是稳定的，上一步具有相同交易时间的事务在第二轮排序后的相对顺序是不变的，而若算法不稳定第二轮对交易时间的排序会破坏第一轮排序的成果。显然我们在这种情况下更希望排序算法是稳定的。

    我们前面介绍的几种算法中，稳定的排序算法有冒泡排序、插入排序和归并排序，而选择排序、希尔排序、快速排序和堆排序都是不稳定的。

2. 原地排序

    所谓的原地排序指的是对待排数组进行排序时只需在原数组处来回移动数组元素来实现排序。我们之前介绍的排序算法中，原地排序的算法有：选择排序、插入排序、希尔排序、快速排序与堆排序；非原地排序算法只有归并排序（我们使用了tmpArray来辅助排序）。   

六、实战名企面试题

    这一部分我们来一起解决几道一线互联网企业的关于排序的面试/笔试题，以检验我们的学习成果以及能够让我们在以后的面试中增添一份信心。

【2015阿里巴巴研发工程师笔试题】个数约为50K的数列需要进行从小到大排序，数列特征是基本逆序(多数数字从大大小，个别乱序)，以下哪种排序算法在事先不了解数列特征的情况下性能最优。（ ） A. 冒泡排序　　B. 改进冒泡排序　　C. 选择排序　　D. 快速排序　　E. 堆排序　　F.插入排序

     根据题目中的描述，首先我们可以排除A、B、C，因为它们的时间复杂度都是O(n)。接下来我们看下D选项，我们前面提到过，快速排序在最坏情况下的时间复杂度会退化至O(n^2)，F选项的插入排序在逆序数很大时性能也很差（O(n^2)）。而堆排序在最坏情况下的复杂度也为O(logn)，所以这里我们应该选择堆排序。

 【2016阿里巴巴校招笔试题】现有1GB数据进行排序，计算资源只有1GB内存可用，下列排序方法中最可能出现性能问题的是（ ）

A. 堆排序　　B. 插入排序　　C. 归并排序　　D. 快速排序　　E. 选择排序　　F. 冒泡排序

    根据题目的描述，我们能够很明确的知道这道题考察我们的是原地排序的概念，这里我们只需要选择非原地排序的占用额外空间最大的算法，显然答案是”C. 归并排序"。

【京东】假设你只有100Mb的内存，需要对1Gb的数据进行排序，最合适的算法是（ ）

A. 归并排序　　B. 插入排序　　C. 快速排序　　D. 冒泡排序

    根据题目，我们可以知道，我们现有的内存限制使得我们无法把数据一次性加载到内存中，所以我们只能先加载一部分数据，对其排序后存入磁盘中。然后再加载一些数据，把它们“合并”到已排序的数据集中去，重复这个过程直到排序完成，显然最能胜任这个工作的是归并排序。

【选自《剑指offer》】输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。

    初看这道题，根据前面的介绍，我们立刻就能够想好几种方案：

    第一个方案是使用（最小）优先队列。具体方法就是把输入数组input中的元素都添加到优先队列中，然后调用k次delMin方法我们就能欧得到最小的k个数字。相信这种解法的代码在理解了优先队列的实现后我们大家都能写出来。

    第二个方案是使用冒泡排序k轮。

    第三个方案是使用快速排序中的partition方法。我们知道partition方法会返回一个索引j，会把原数组切分为a[low..j-1]（所包含元素均小于等于a[j]）和a[j..high]（所包含的元素都大于等于a[j]，N为输入数组的尺寸）。这里我们初始化low为0，high为input..length-1，然后调用partition方法。若返回的j等于k-1（意味着a[low..j]中的元素数等于k），则返回a[low..j]即可；若j大于k-1（意味着a[low..j]包含的元素数大于k），此时我们把partition的high参数更新为j-1；若j小于k-1（意味着a[low..j]的元素数小于k，此时我们把low更新为j+1）。以上情况中，只要j不等于k-1，我们就根据j的与k-1的关系更新low或是high然后继续调用partition方法，直到返回的j等于k-1。具体实现代码如下：

public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) {
    if (input == null) {
        return null;
    }
    ArrayList<Integer> list = new ArrayList<Integer>(k);
    int low = 0;
    int high = input.length - 1;
    int j = partition(input, low, high);
    while (j != k-1){
        if (j > k-1){
            high = j - 1;
        } else {
            low = j + 1;
        }
        j = partition(input, low, high);
    }

   for (int i = 0; i < k; i++) {
       list.add(input[i]);
   }
   return list;
}
   
private static int partition(int[] a, int low, int high) {
    int i = low;
    int j = high + 1;

    int p = a[low];
    while (true) {
        while (a[++i] < p) {
            if (i == high) {
                break;
            }
        }

        while (a[--j] > p) {
            if (j == low) {
                break;
            }
        }

        if (i >= j) {
            break;
        }
        exchange(a, i, j);
    }
    exchange(a, low, j);
    return j;
}