主流排序简单集合

排序算法集合

选择排序

• 图解：
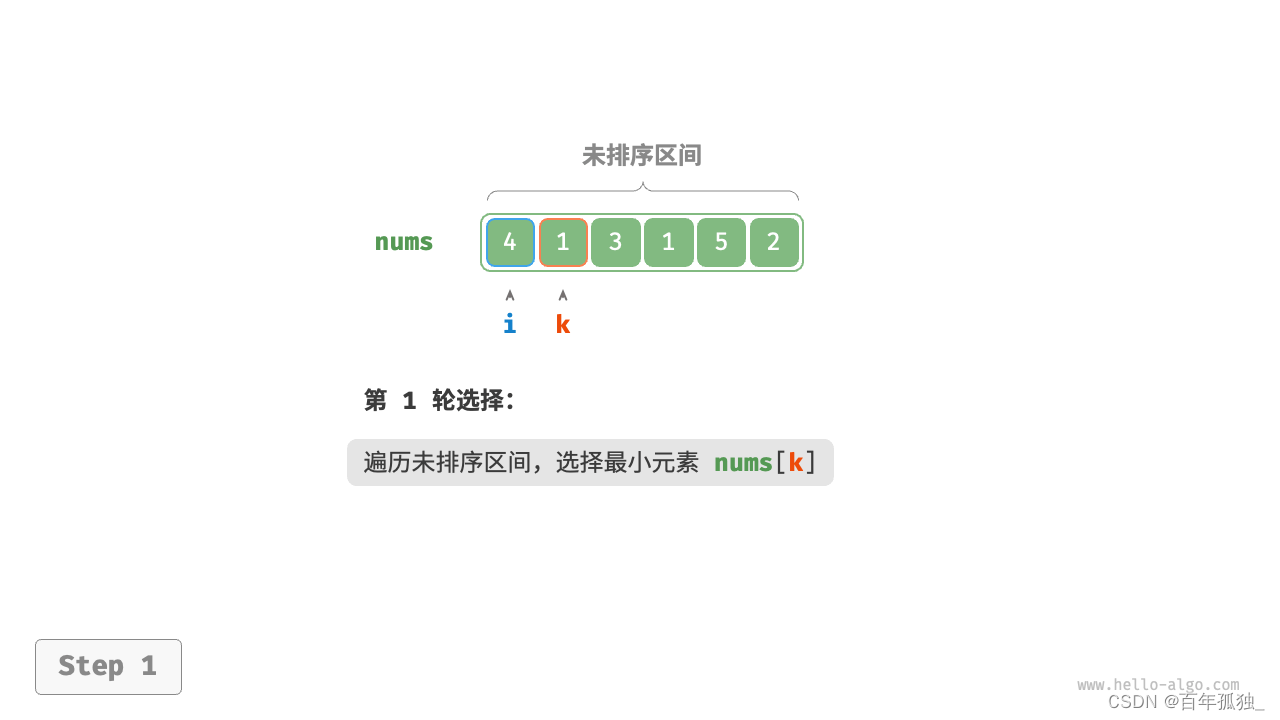
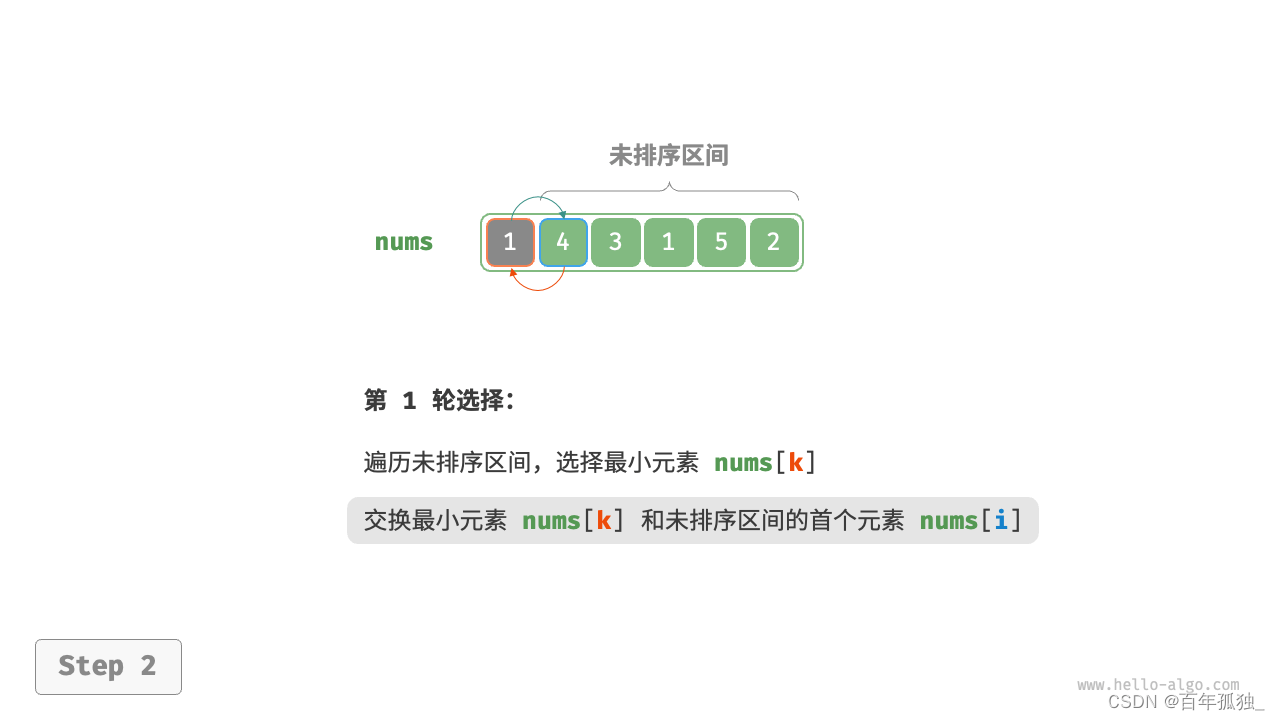
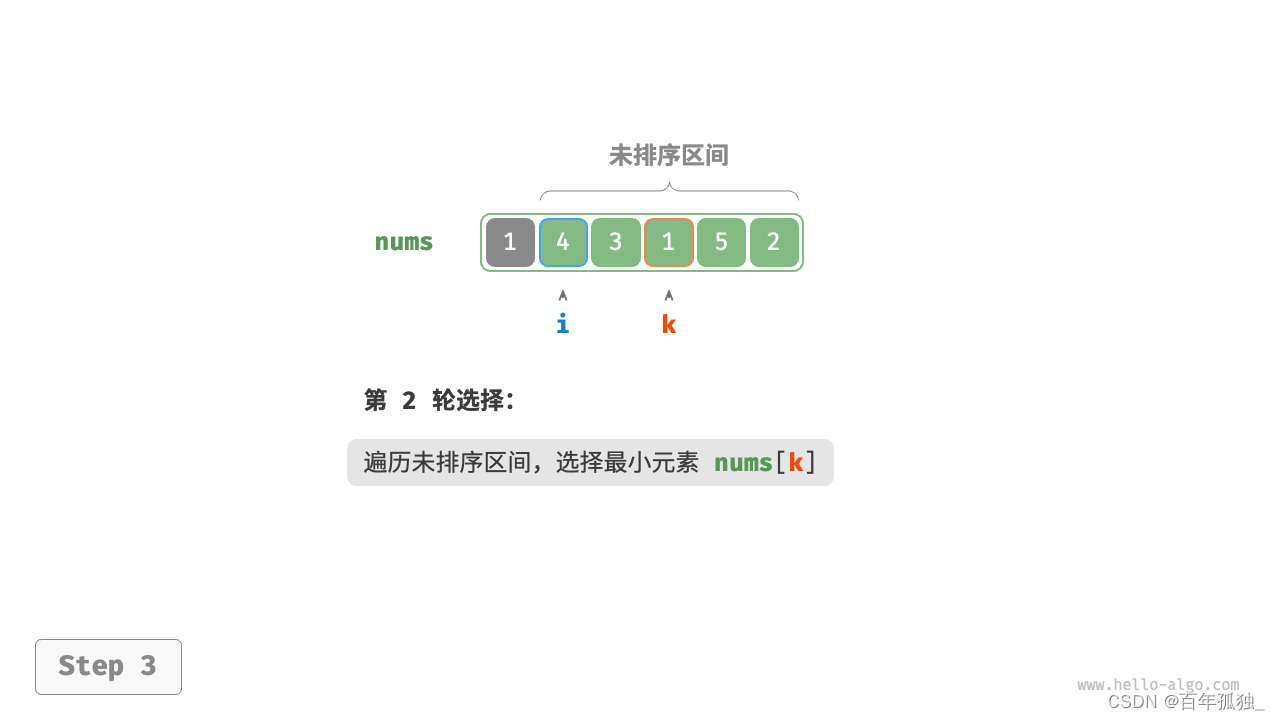
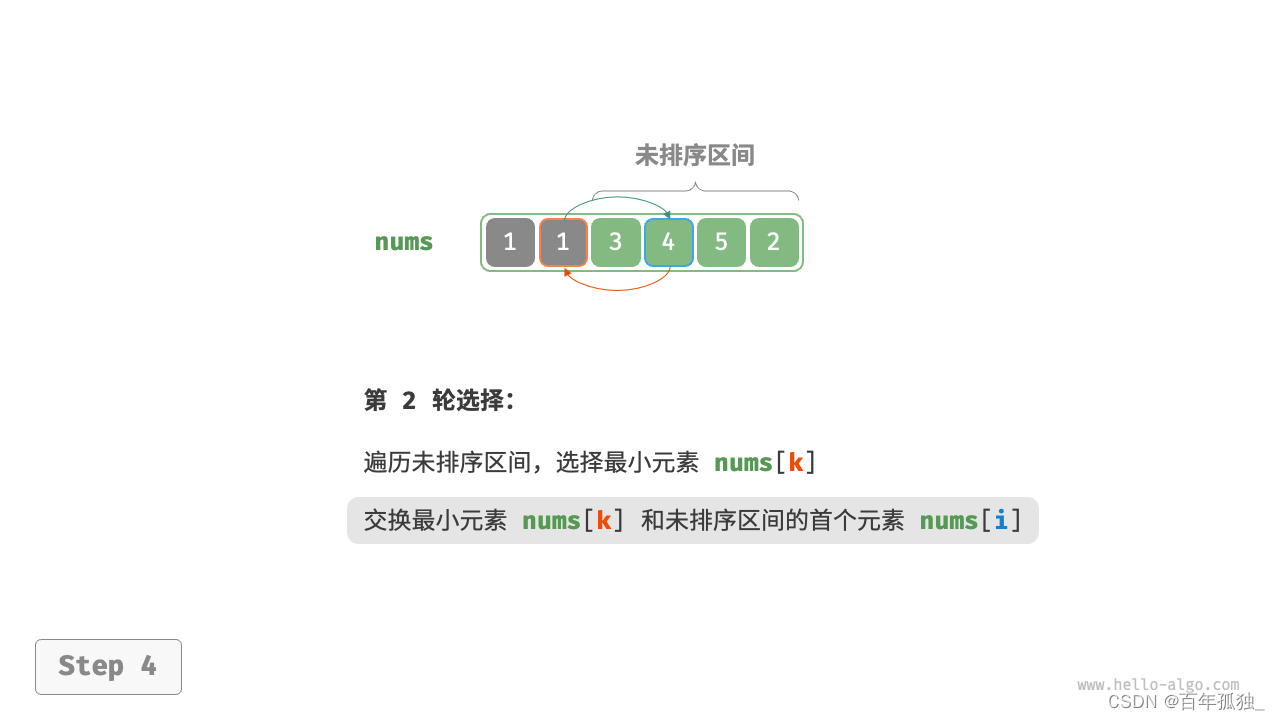
• 以此类推直至

/*选择排序*/
void select_sort(vector<int>& nums) {
	/*选取一个基准元素逐个与后面的比较*/
	for (int i = 0; i < nums.size() - 1-1; i++) {
		int min = i;/*定义随之变化的基准元素*/
		for (int j = i + 1; j < nums.size() - 1; j++) {
			if (nums[i] > nums[j]) {
				swap(nums[i], nums[j]);//交换元素
			}
		}
	}
}

/* 选择排序 */  官方正解
void selectionSort(vector<int>& nums) {
	int n = nums.size();
	// 外循环：未排序区间为 [i, n-1]
	for (int i = 0; i < n - 1; i++) {
		// 内循环：找到未排序区间内的最小元素
		int k = i;
		for (int j = i + 1; j < n; j++) {
			if (nums[j] < nums[k])
				k = j; // 记录最小元素的索引
		}
		// 将该最小元素与未排序区间的首个元素交换
		swap(nums[i], nums[k]);
	}
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

冒泡排序（经典）

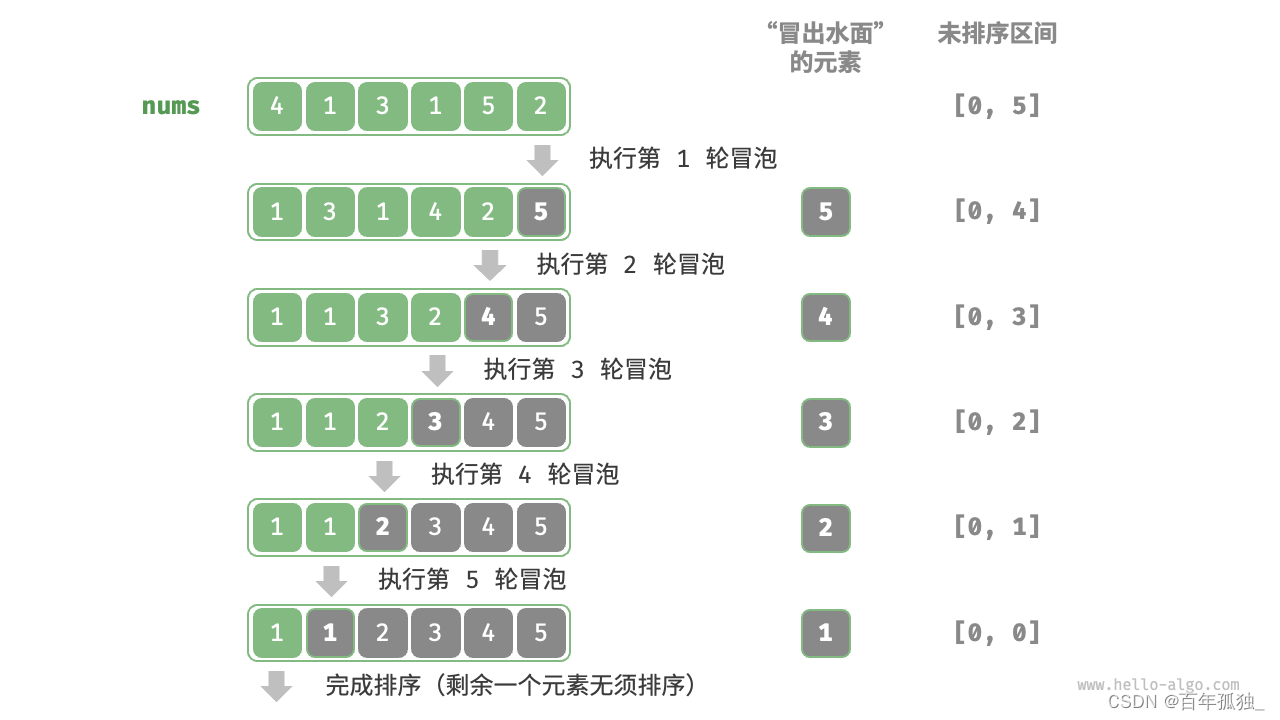
/* 冒泡排序 */
void bubbleSort(vector<int>& nums) {
	// 外循环：未排序区间为 [0, i]
	for (int i = nums.size() - 1; i > 0; i--) {
		// 内循环：将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
		for (int j = 0; j < i; j++) {
			if (nums[j] > nums[j + 1]) {
				// 交换 nums[j] 与 nums[j + 1]
				// 这里使用了 std::swap() 函数
				swap(nums[j], nums[j + 1]);
			}
		}
	}
}

void test() {
	vector<int> nums = { 4,23,6,12,56,78,2,3,5,76 };
	//select_sort(nums);
	bubbleSort(nums);
	for (int num : nums) {
		cout << num << " ";
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

插入排序

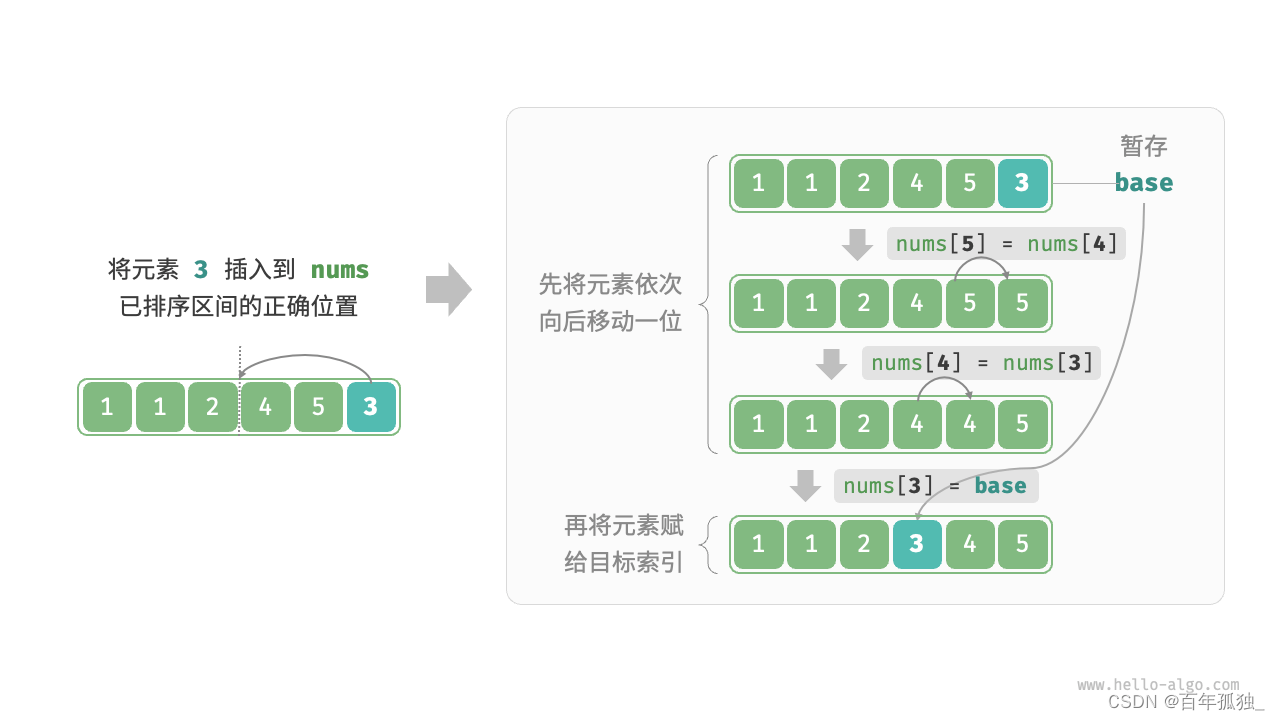
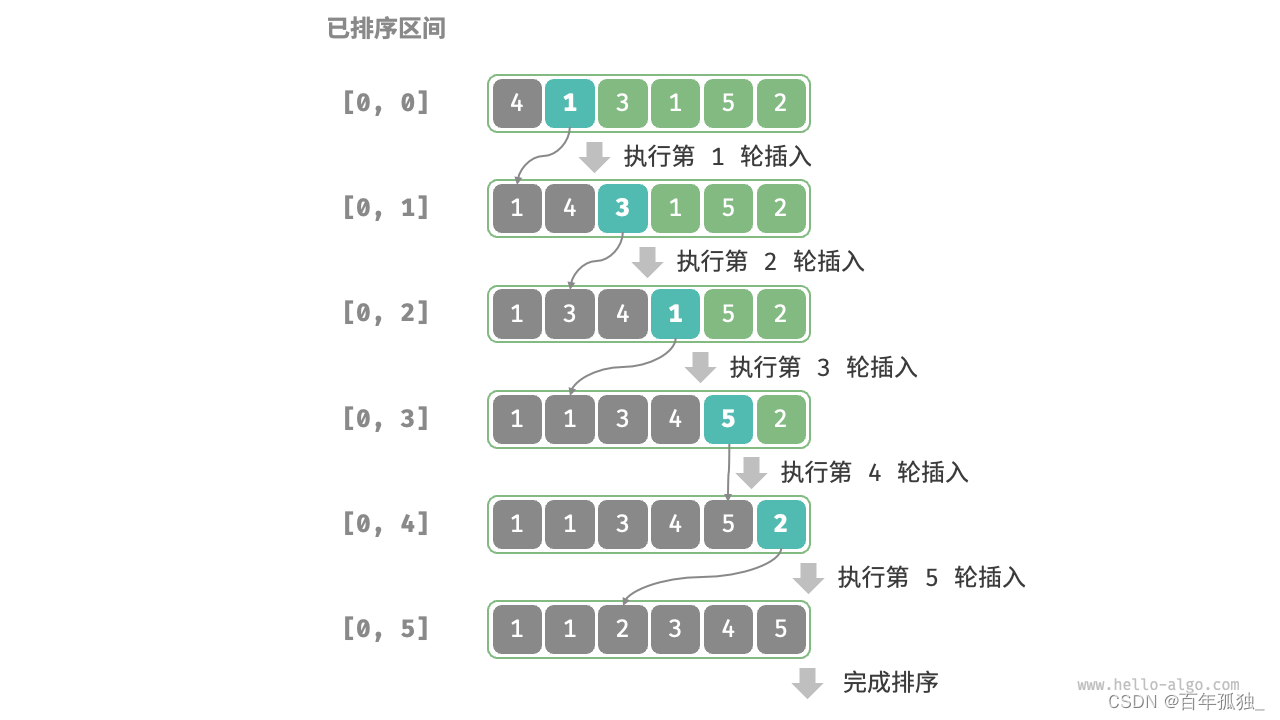
/* 插入排序 */
void insertionSort(vector<int> &nums) {
    // 外循环：已排序区间为 [0, i-1]
    for (int i = 1; i < nums.size(); i++) {
        int base = nums[i], j = i - 1;
        // 内循环：将 base 插入到已排序区间 [0, i-1] 中的正确位置
        while (j >= 0 && nums[j] > base) {
            nums[j + 1] = nums[j]; // 将 nums[j] 向右移动一位
            j--;
        }
        nums[j + 1] = base; // 将 base 赋值到正确位置
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

快速排序

重点理解反复熟悉

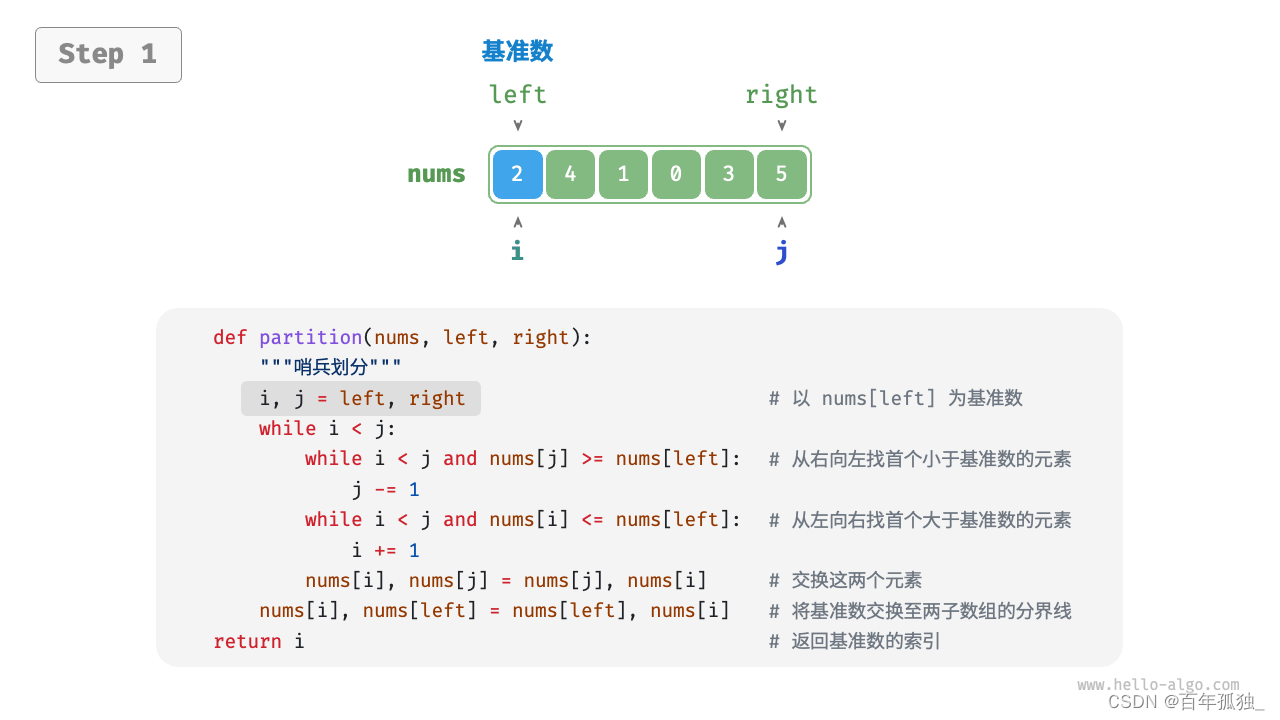
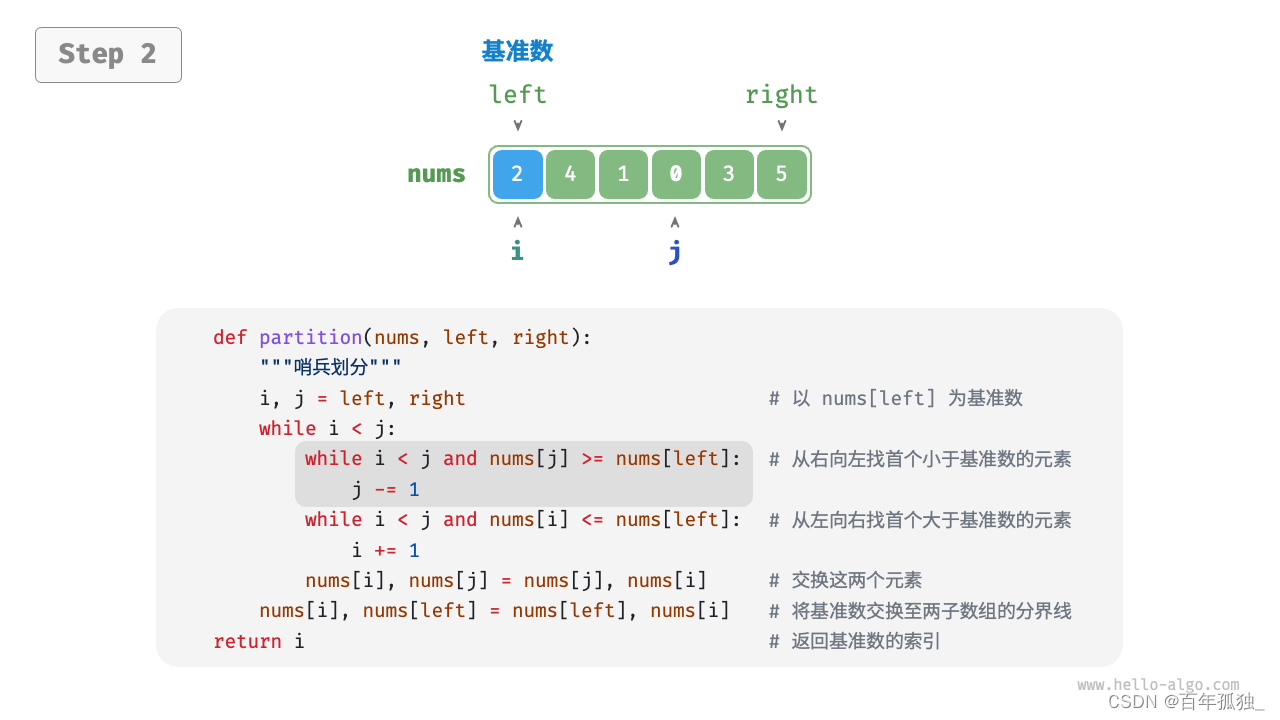
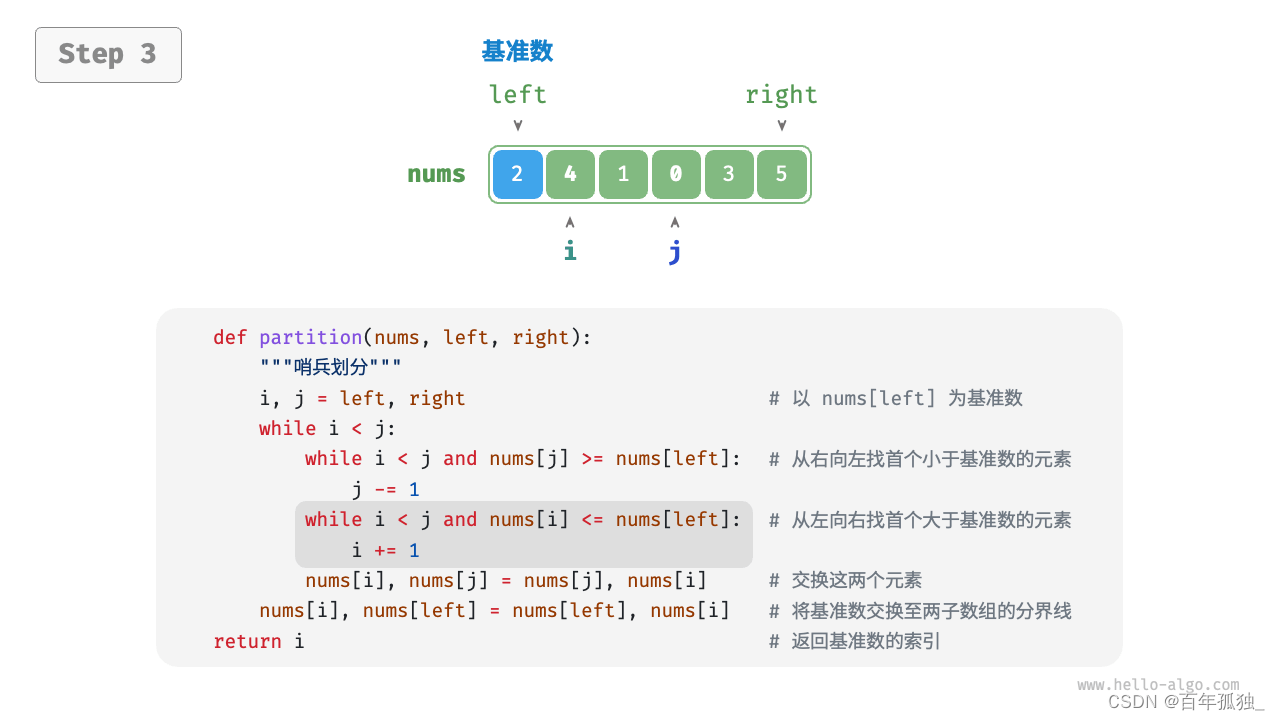
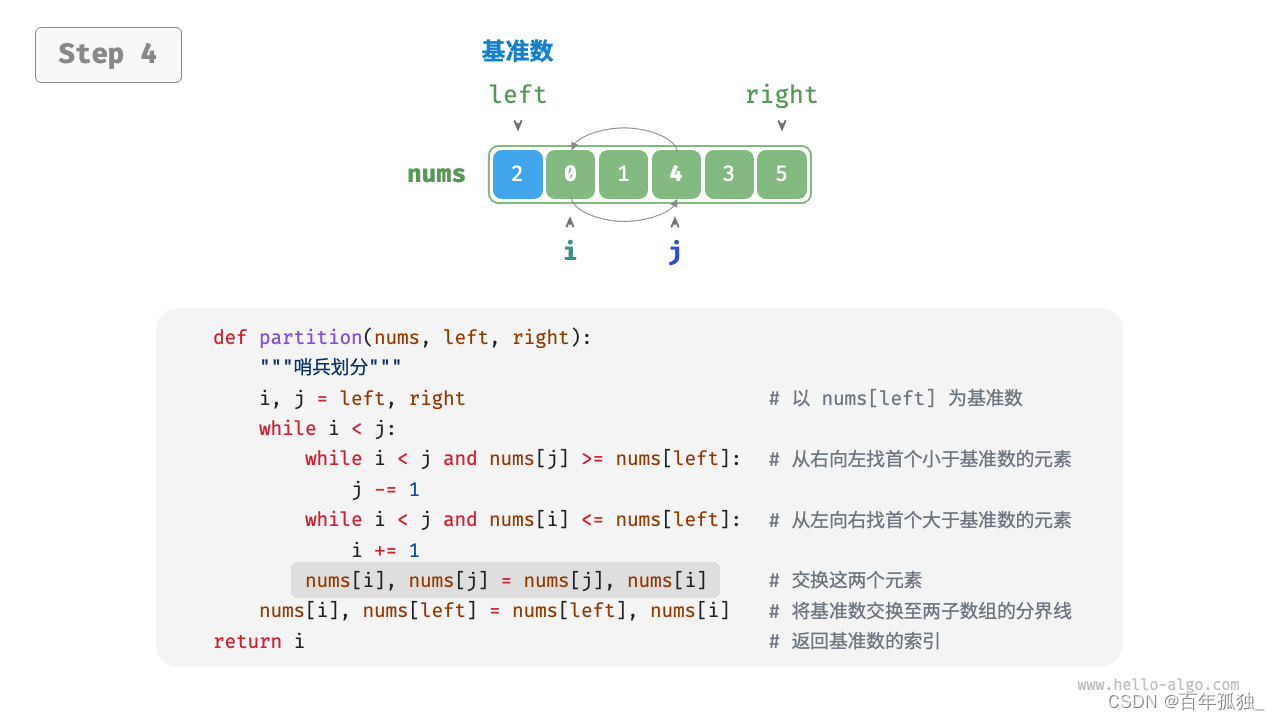
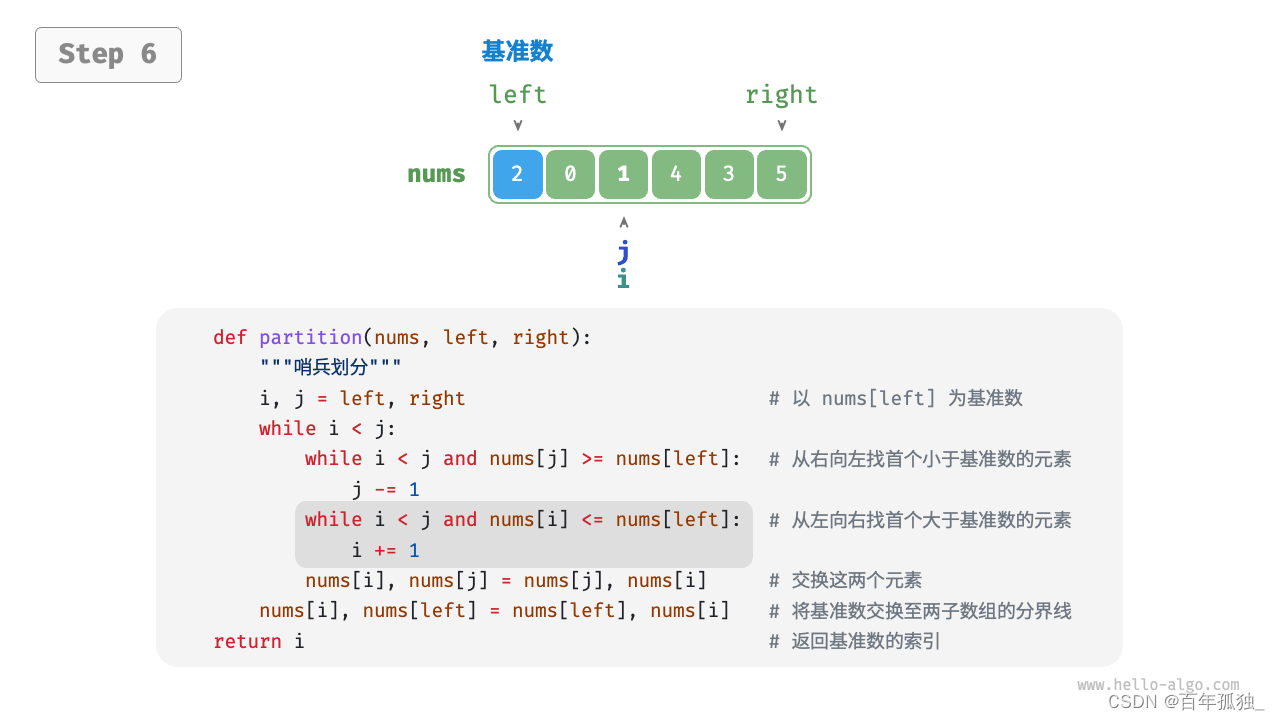
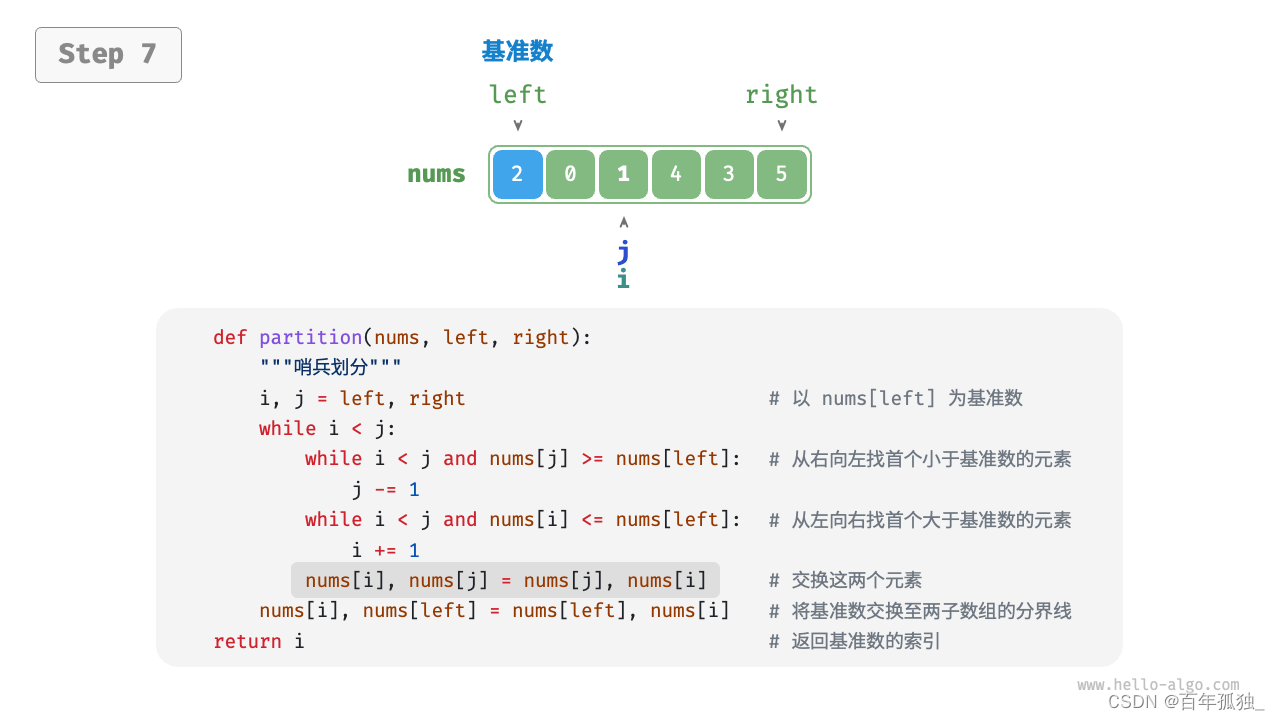
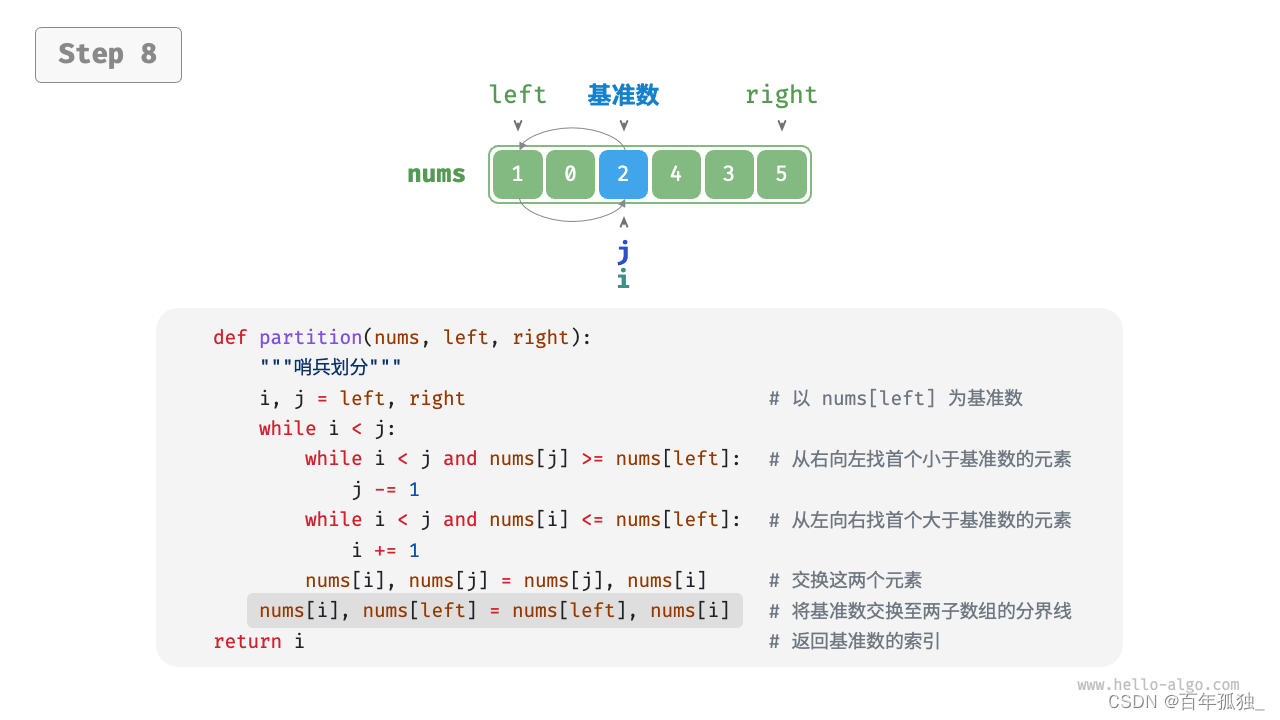
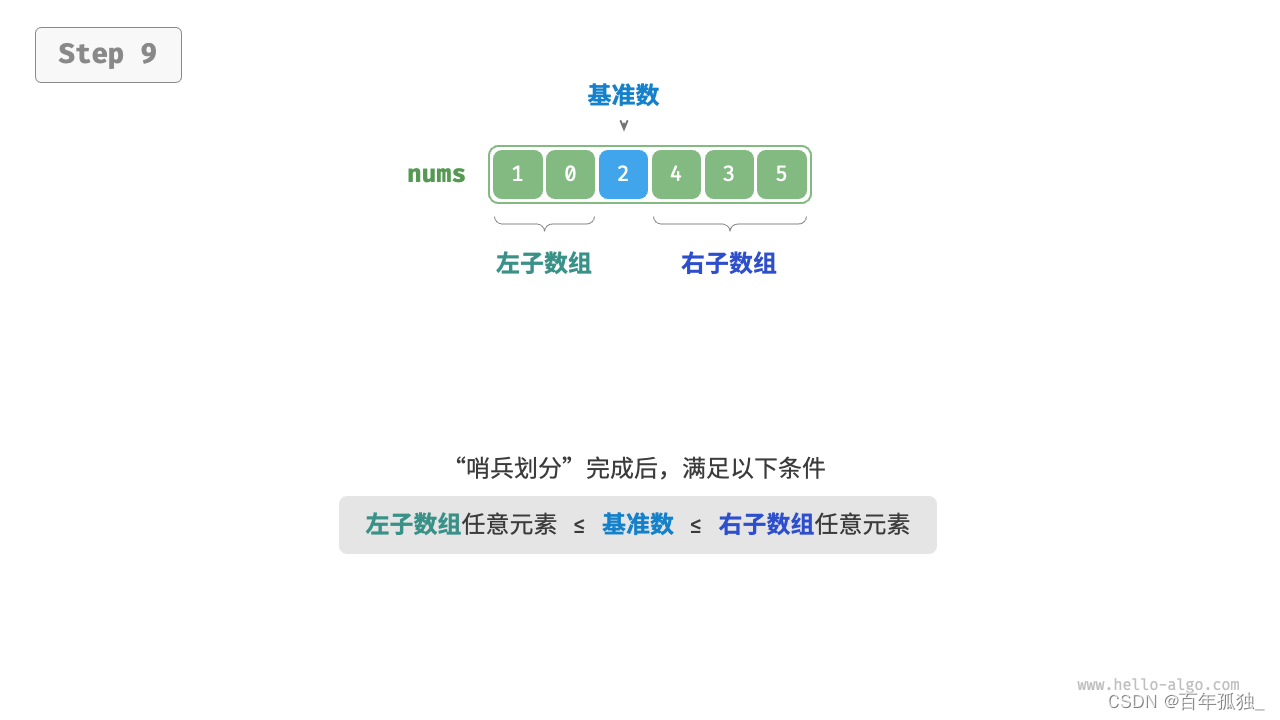
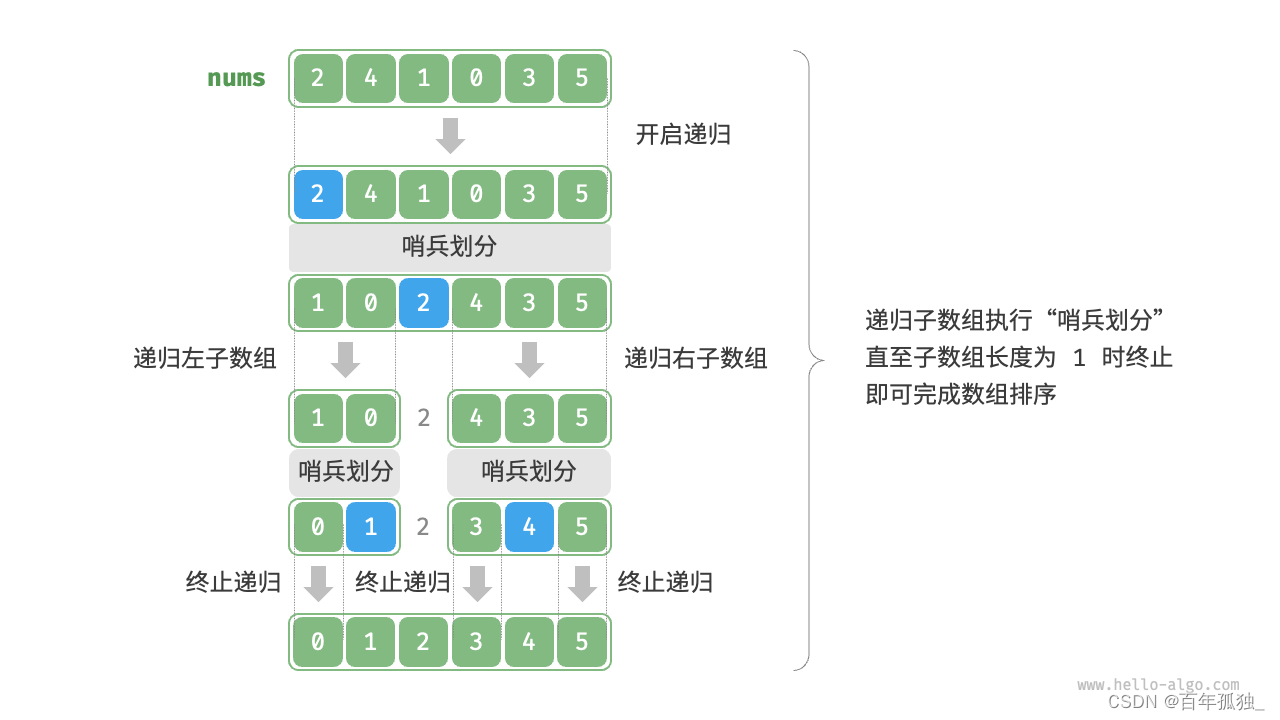
/* 元素交换 */
void swap(vector<int>& nums, int i, int j) {
	int tmp = nums[i];
	nums[i] = nums[j];
	nums[j] = tmp;
}

/* 哨兵划分 */
int partition(vector<int>& nums, int left, int right) {
	// 以 nums[left] 为基准数
	int i = left, j = right;
	while (i < j) {
		while (i < j && nums[j] >= nums[left])
			j--; // 从右向左找首个小于基准数的元素
		while (i < j && nums[i] <= nums[left])
			i++;          // 从左向右找首个大于基准数的元素
		swap(nums, i, j); // 交换这两个元素
	}
	swap(nums, i, left); // 将基准数交换至两子数组的分界线
	return i;            // 返回基准数的索引
}

/* 快速排序 */
void quickSort(vector<int>& nums, int left, int right) {
	// 子数组长度为 1 时终止递归
	if (left >= right)
		return;
	// 哨兵划分
	int pivot = partition(nums, left, right);
	// 递归左子数组、右子数组
	quickSort(nums, left, pivot - 1);
	quickSort(nums, pivot + 1, right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

堆排序

参考：数据结构之堆火烨烨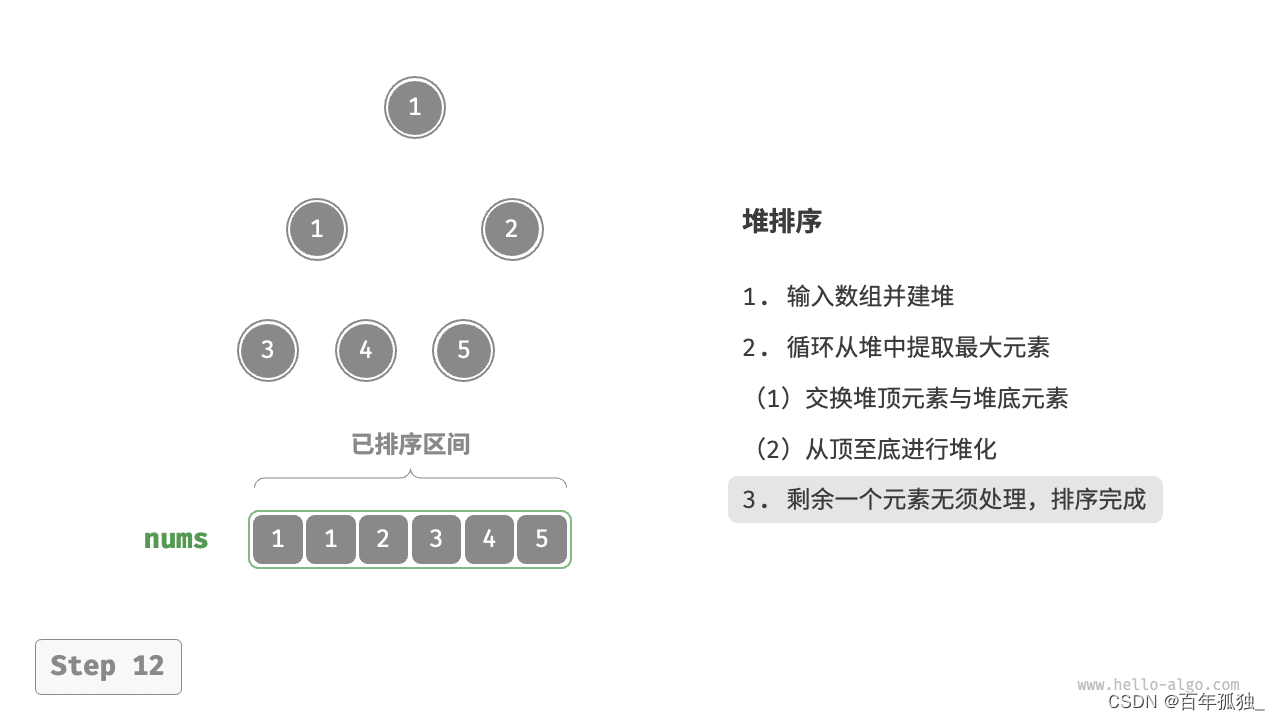

#include <vector>
#include <iostream>
#include <algorithm> // 引入 swap 函数

using namespace std;

// 向下调整堆
void siftDown(vector<int>& nums, int n, int i) {
    while (true) {
        int l = 2 * i + 1;
        int r = 2 * i + 2;
        int ma = i;
        if (l < n && nums[l] > nums[ma])
            ma = l;
        if (r < n && nums[r] > nums[ma])
            ma = r;
        if (ma == i) {
            break;
        }
        swap(nums[i], nums[ma]);
        i = ma;
    }
}

/* 堆排序 */
void heapSort(vector<int>& nums) {
    int n = nums.size();
    // 建堆操作
    for (int i = n / 2 - 1; i >= 0; --i) {
        siftDown(nums, n, i);
    }
    // 提取最大元素并重新建堆
    for (int i = n - 1; i > 0; --i) {
        swap(nums[0], nums[i]);
        siftDown(nums, i, 0);
    }
}

int main() {
    vector<int> nums = { 10, 30, 40, 20, 100 };
    cout << "Before sorting: ";
    for (int num : nums) {
        cout << num << " ";
    }
    cout << endl;

    heapSort(nums);

    cout << "After sorting: ";
    for (int num : nums) {
        cout << num << " ";
    }
    cout << endl;

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

桶排序

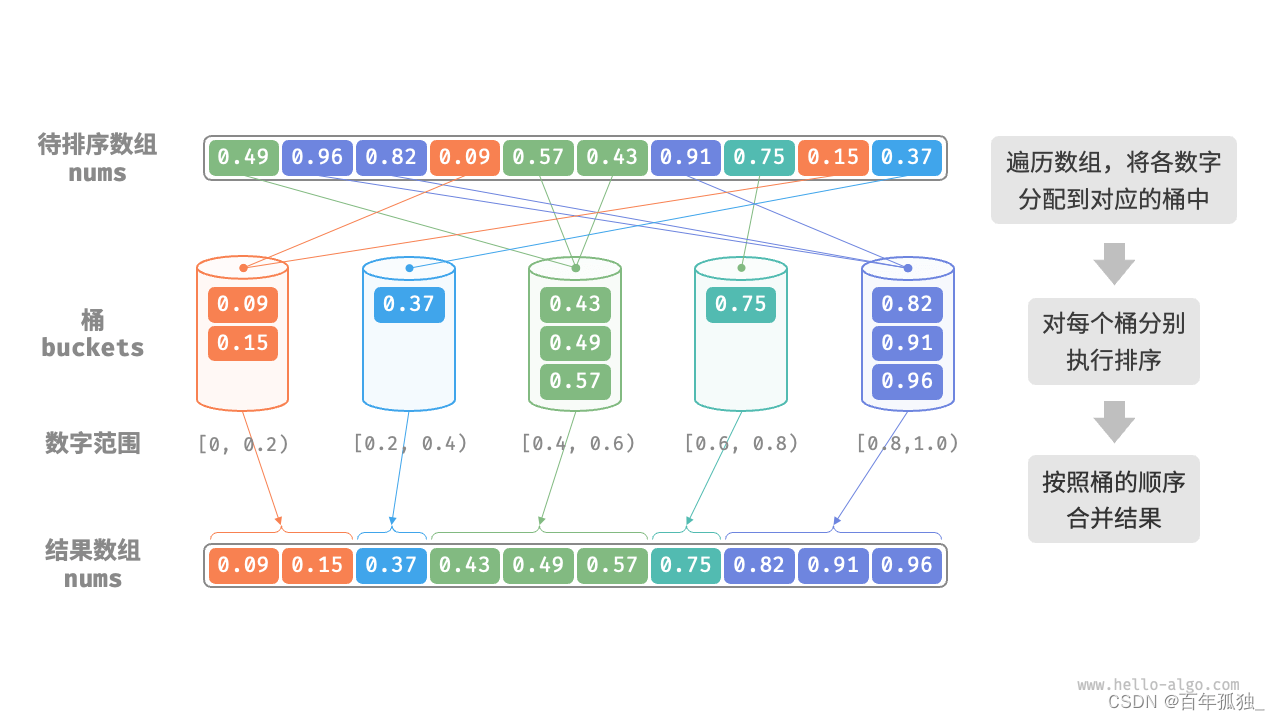
/* 桶排序 */
void bucketSort(vector<float> &nums) {
    // 初始化 k = n/2 个桶，预期向每个桶分配 2 个元素
    int k = nums.size() / 2;
    vector<vector<float>> buckets(k);
    // 1. 将数组元素分配到各个桶中
    for (float num : nums) {
        // 输入数据范围为 [0, 1)，使用 num * k 映射到索引范围 [0, k-1]
        int i = num * k;
        // 将 num 添加进桶 bucket_idx
        buckets[i].push_back(num);
    }
    // 2. 对各个桶执行排序
    for (vector<float> &bucket : buckets) {
        // 使用内置排序函数，也可以替换成其他排序算法
        sort(bucket.begin(), bucket.end());
    }
    // 3. 遍历桶合并结果
    int i = 0;
    for (vector<float> &bucket : buckets) {
        for (float num : bucket) {
            nums[i++] = num;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

难点：归并排序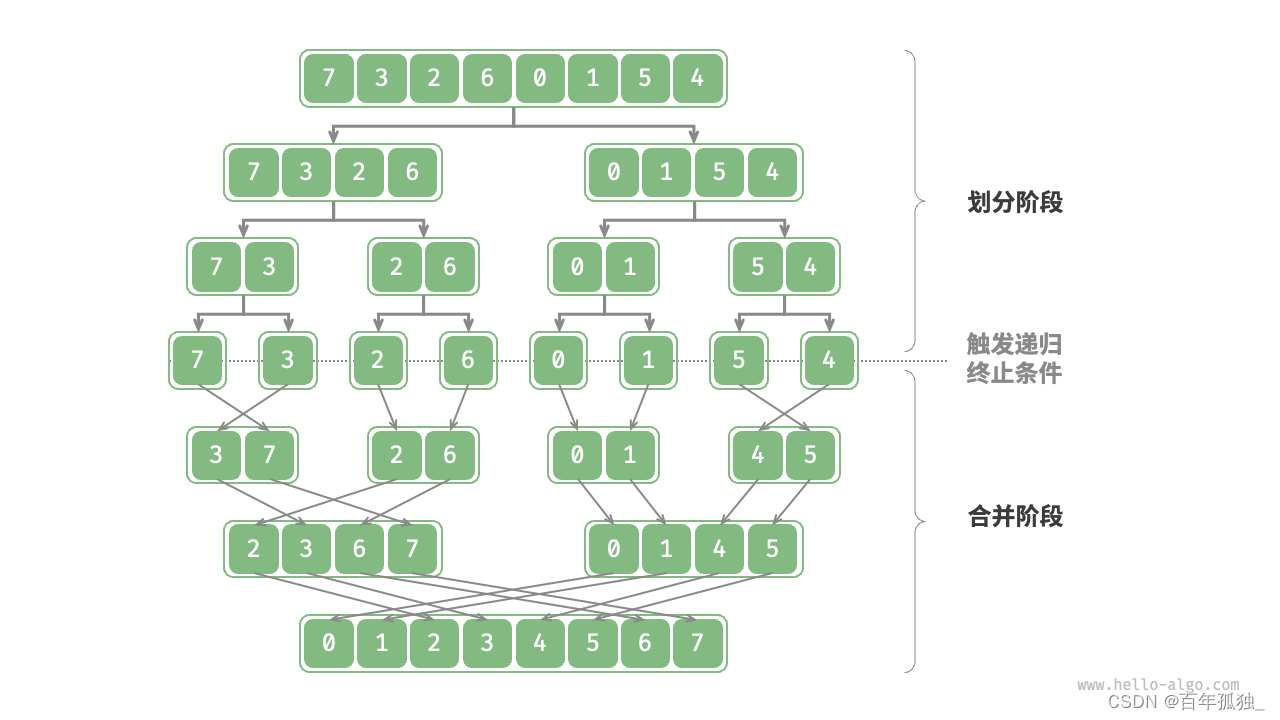

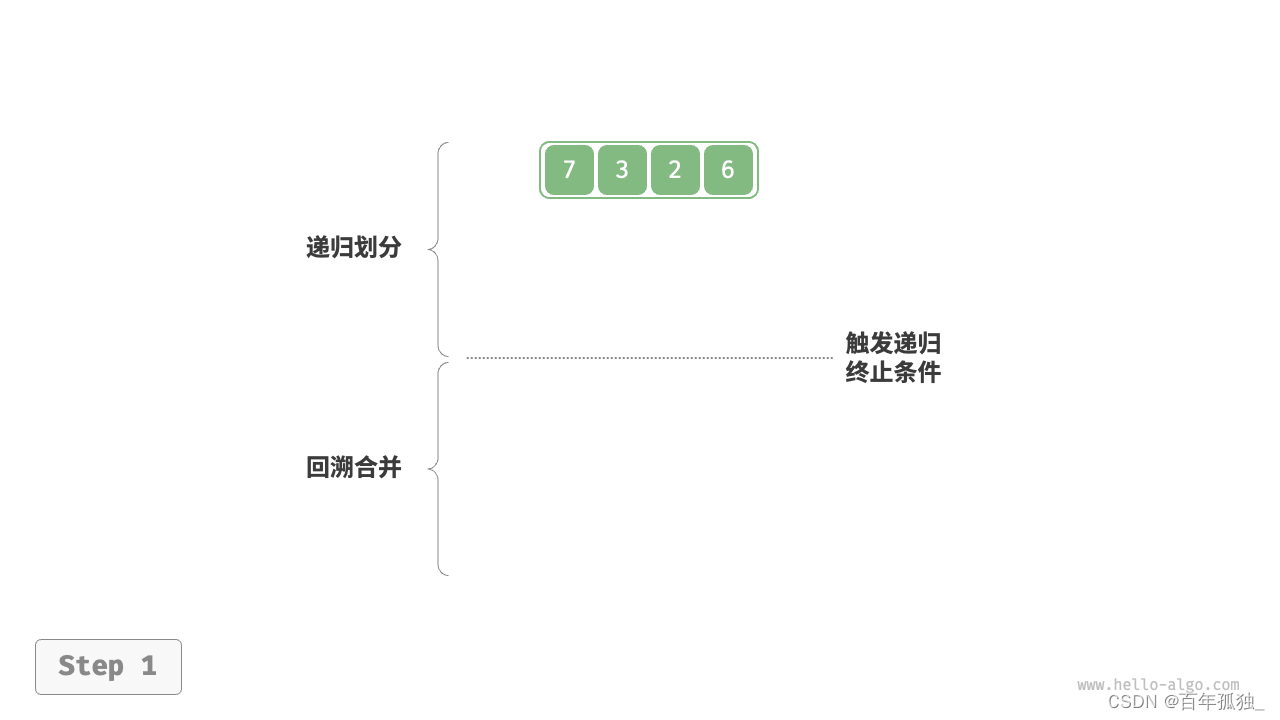
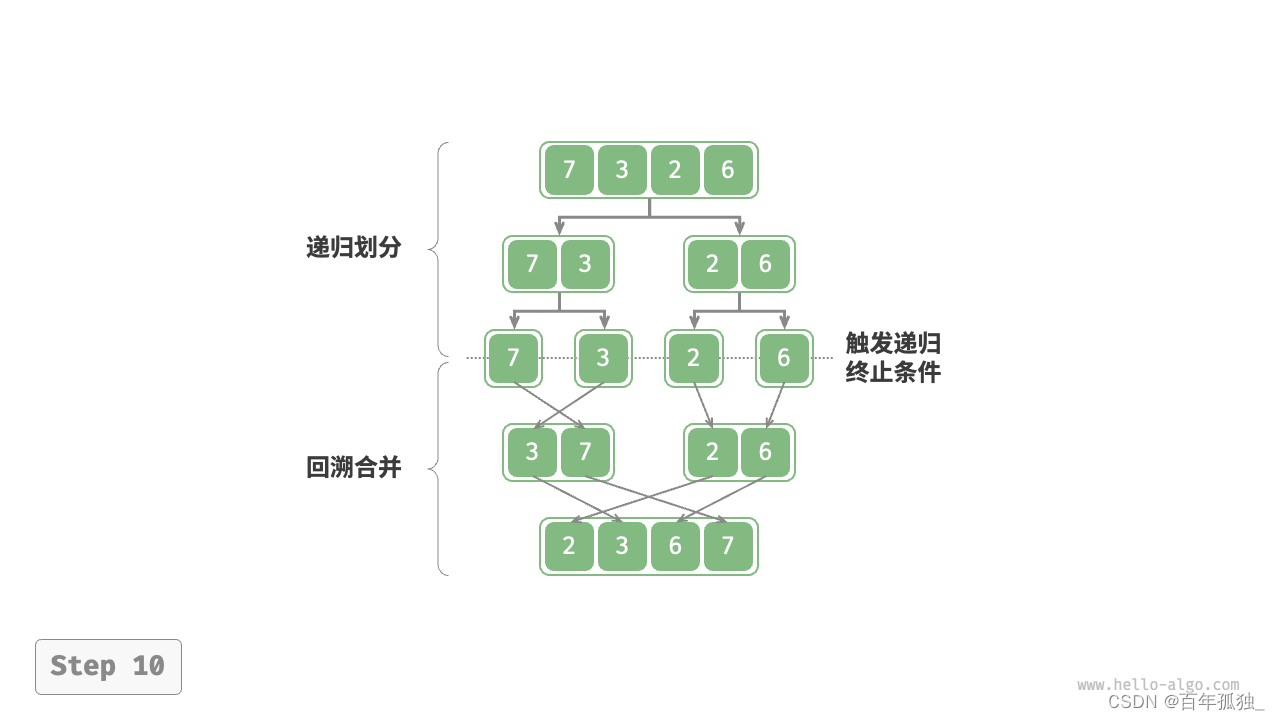
实现

/* 合并左子数组和右子数组 */
void merge(vector<int> &nums, int left, int mid, int right) {
    // 左子数组区间为 [left, mid], 右子数组区间为 [mid+1, right]
    // 创建一个临时数组 tmp ，用于存放合并后的结果
    vector<int> tmp(right - left + 1);
    // 初始化左子数组和右子数组的起始索引
    int i = left, j = mid + 1, k = 0;
    // 当左右子数组都还有元素时，进行比较并将较小的元素复制到临时数组中
    while (i <= mid && j <= right) {
        if (nums[i] <= nums[j])
            tmp[k++] = nums[i++];
        else
            tmp[k++] = nums[j++];
    }
    // 将左子数组和右子数组的剩余元素复制到临时数组中
    while (i <= mid) {
        tmp[k++] = nums[i++];
    }
    while (j <= right) {
        tmp[k++] = nums[j++];
    }
    // 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间
    for (k = 0; k < tmp.size(); k++) {
        nums[left + k] = tmp[k];
    }
}

/* 归并排序 */
void mergeSort(vector<int> &nums, int left, int right) {
    // 终止条件
    if (left >= right)
        return; // 当子数组长度为 1 时终止递归
    // 划分阶段
    int mid = (left + right) / 2;    // 计算中点
    mergeSort(nums, left, mid);      // 递归左子数组
    mergeSort(nums, mid + 1, right); // 递归右子数组
    // 合并阶段
    merge(nums, left, mid, right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

浅谈：

**好像人生在某一时期的青春过去之后时间的流逝变得始料未及的迅速，梦里不知身是客，一晌贪欢。就像古装台词描述的一样：俗世洪流，能够站得住脚就已经是千辛万苦。不知何时，对于某些理想性的事物的渴求也变得木讷了起来。当然，人们都喜欢向阳而生的少年/少女，尤其是久处黑夜的行路人，对于那爽朗的性格，明亮的笑容总是不由自主的喜欢与偏向。但是我的感觉总觉得人生不如意十有八九，身不由己，己不由心或许才是众生之态。好像这条路一眼可以望到尽头，可总充满不知所云的迷雾与诱惑。

依稀记得多年前看过一本书，刘同《你的孤独，虽败犹荣》当时并没有怎么仔细看，只是这名字很独特，感觉很有意思，竟然也默默记在心上。好多年后，走了也算多的路（虽然到现在也只是个迷途的旅客），见了很多的人，自然亦是失去了太多，不知竟也变得离经叛道起来。偶然间回忆起这本书，突然明白这书名的涵义。 你的孤独虽败犹荣！！！！就是当你已经选择了这条不被理解的道路，你是否有勇气走下去，有勇气坚定的走下去，是否做好了孤注一掷（虽说有些夸张，对于我等凡夫俗子）,做好了接受失败的必然结局！就像感情中所失去的那样，

**很多年后，如果再给你一次机会，你会选择重新再来吗？**年少不可得之物终会困其一生，或许只是执念太过深沉，思维困在了自我的藩篱。但是，如果可以，你又会如何？你真愿意？你真的想清楚了吗？ 我想人是感性的，不是坏事，也是难得，理性倒也十分需要，但是感性足以使得我们面对糟粕的世界本身。去年元夜时，花市灯如昼。 月上柳梢头，人约黄昏后。 今年元夜时，月与灯依旧。 不见去年人，泪湿春衫袖。

如果可以，可以在评论区留下你的遗憾，亦或是那个年少时曾照耀你的月光！！！ 我的意思是,你值得珍藏过去，值得开拓未来！**