算法与数据结构（基于Go语言）学习笔记01

算法初识：汉诺塔问题(Towers of Hanoi)

规则简介

​ 给定三根柱子，记为 $A$、$B$、 $C$，其中 $A$ 柱子上有$n-1$ 个盘子，从上至下盘子越来越大。问：将$A$柱上的盘子经由$B$柱，移动到$C$柱最少需要多少次？每次应该怎么搬运？

​移动时应注意：①一次只能移动一个盘子；②大的盘子不能压在小盘子上。

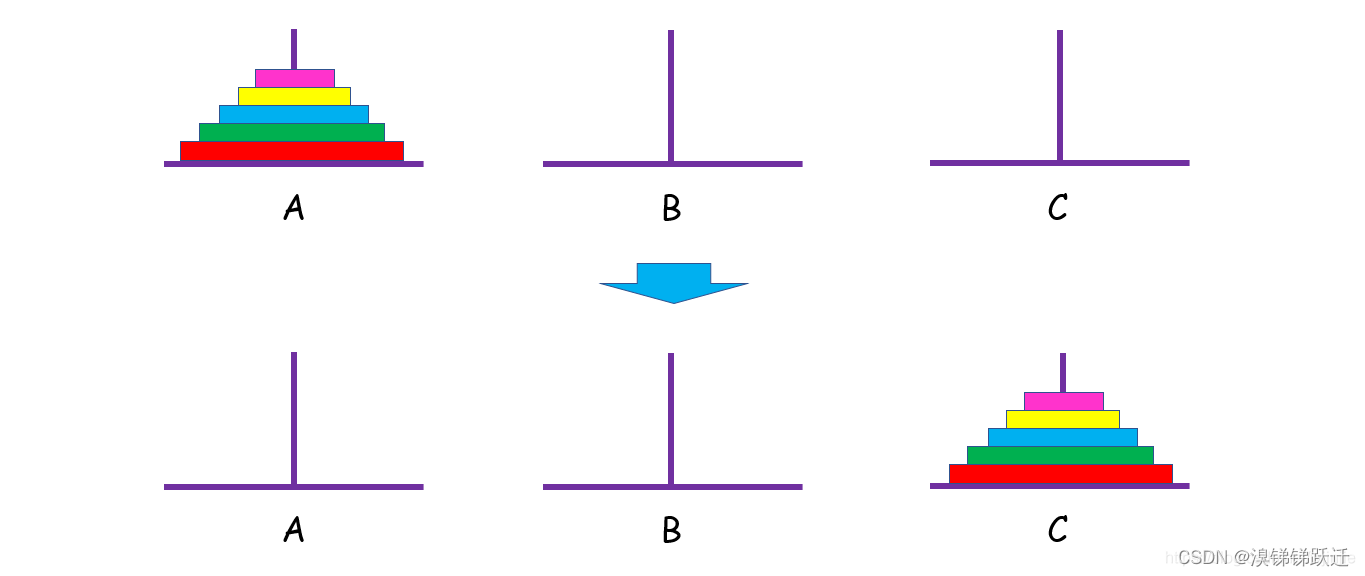
方法概述：递归法

宏观来看，我们首先需要将最大的底盘和其他盘分离开来，这样才有机会将底盘先放到$C$柱上。如果最大底盘和其他盘已经分开，其他盘肯定不能堆在$C$柱，否则我们不可能将最大底盘放到$C$柱底部。因此其他盘一定是堆砌在$B$柱的。
我们顺利将最大的底盘移动到了目标位置，而现在剩下的盘子都在$B$处。让我们忘掉最大的底盘，现在的任务是将$n-1$个盘子从$B$移动到$C$。
如何思考这个问题呢？注意多个盘子的绝对位置没有意义，如果要移动多个盘子，直接移动是不行的，一定要有中介。
因此，将$n-1$个盘子从$B$移动到$C$的情形和将$n-1$个盘子从$A$移动到$C$是完全类似的！
下面让我们假设一个函数：

func hanoi(n int, a, b, c string) {
	...
}
1
2
3

函数头为hanoi(n, a, b, c)，意思为将$n$个盘子从a经由b移动到c（注意多个盘子不能直接从a移动到c，所以必须有中介）。
综上，我们可以将$n$个盘子的汉诺塔任务分解为以下三步：

1. 将$n-1$个盘子从$A$经由$C$移动到$B$；
2. 将最大底盘从$A$直接移动到$C$；
3. 将$n-1$个盘子从$B$经由$A$移动到$C$.
   从中我们明显看出了递归的影子。注意递归方法的重点在于将关于$n$的问题拆解成若干关于$n-1$的问题，从而用后者来清晰有效地表达出前者的内含结构。除此之外，递归必须包含终止条件。在这个问题中，终止条件就是$n\le 0$。

代码实现

func hanoi(n int, a, b, c string) {
	if n > 0 {
		hanoi(n - 1, a, c, b)
		fmt.Printf("Moving from %s to %s", a, c)
		hanoi(n - 1, b, a, c)
	}
}
1
2
3
4
5
6
7

搜索问题

搜索问题在生活和编程中都很常见，即给定一组数据和一个目标数据，需要找到目标数据对应的索引并返回。

暴力实现：线性查找(linear search)

func linear_search(arr []int, elem int) int {
	for k, v := range arr {
		if elem == v {
			return k
		}
	}
	return -1
}
1
2
3
4
5
6
7
8

当找不到目标数据时，我们返回-1。这种方法的复杂度显然是$O(n)$级别的。

二分查找(binary search)

对于有序数组，我们还可以使用二分法进行查找。

func binary_search(arr []int, elem int) int {
	//只能用于有序列表
	left, right := 0, len(arr)-1
	for left <= right {
		mid := left + (right-left)/2
		if arr[mid] == elem {
			return mid
		} else if elem < arr[mid] {
			left = mid + 1
		} else {
			right = mid - 1
		}
	}
	return -1
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

例如在军训时需要按照身高从大到小（从左到右）进行排队，而我想在其中找到一个高为175cm的学生，我可以从队伍的中间先进行比对。如果队伍中间学生的身高高于175cm，说明我想找的学生更靠近队伍末尾，因此我可以将包括中间学生在内的、站在中间学生左边的学生都排除掉，从剩下的学生中进行查找。
注意每次我们都能筛选掉一半的人，因此算法复杂度是$O(lo{g}_{2}n)$的。

排序问题

冒泡排序(bubble sort)

问题分析

排序问题更是经典中的经典，最为直接而暴力的方法就是大名鼎鼎的冒泡排序。
考虑长度为$n$的数组arr，我们想把数组从大到小进行排列。假设索引为$i-1$之前的元素已经排列好了（从大到小），我们接下来对索引为$i$的元素进行排列。

1. 从arr[i+1]遍历到arr[n-1]，即从当前位置遍历到数组末尾；
2. 只要如果遍历到的元素大于当前arr[i]，则交换二者。
   注意此时arr[i]的位置可以说是人来人往，只要arr[i]后面有比自己大的数据，就会被换到arr[i]的位置上。除此之外arr[i]的位置还可以说是风水轮流转，可能某个数据比arr[i]的原始数据大，某个时刻被换到了arr[i]上，但如果后面还有更大的数据，那arr[i]的位子就得腾出来给别人了。
   从上述叙述中我们看出，冒泡排序的内核其实是把从当前位置（即索引为i处）到数组末尾的最大值挑出来放到索引为i处，于是我们的数组就变成了{最大值，次大值，第三最大值，…}

代码实现

func bubbleSort(a []int) []int {
	for i := 0; i < len(a); i++ {
		for j := i + 1; j < len(a); j++ {
			if a[i] < a[j] {
				a[i], a[j] = a[j], a[i]
			}
		}
	}
	return a
}
1
2
3
4
5
6
7
8
9
10

选择排序(selection sort)

问题分析

从冒泡排序的本质我们可以提出另一种算法——选择排序法。
从数组arr中挑选出最大值，将其放入另一个数组res的第一位，随后从arr中删除这一元素。反复重复前述步骤，直到数组arr为空。

代码实现

我们首先使用循环语句实现插入排序：

func selectionSort(a []int, opt SortOption) []int {
	res := make([]int, len(a))
	for i := 0; i < len(res); i++ {
		k0, v0 := 0, 0
		for k, v := range a {
			if v > v0 {
				k0, v0 = k, v
			}
		}
		slices.Delete(a, k0, k0+1)
		res[i] = v0
	}
	return res
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

此外我们可以挑战使用递归法实现这一逻辑：

func selectionSortRecursion(a []int) []int {
	if len(a) == 1 {
		return a
	} else {
		return append(
			[]int{slices.Max(a)},
			selectionSortRecursion(
				slices.Delete(a,
					slices.Index(a, slices.Max(a)),
					slices.Index(a, slices.Max(a)) + 1,
				), opt,)...,
		)
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

插入排序

接下来我们介绍插入排序，这种排序在发牌时很常见。

问题分析

把数组arr当成我们的手牌，假设索引为i之前的牌已经按从大到小的顺序排列好，我们现在从索引为i的牌开始比较。和谁比较呢？和索引为i之前的牌开始比较，我们希望将arr[i]恰好插入到前一张牌比arr[i]大、后一张牌比arr[i]小的位置。
为此，我们从索引为j=i-1处开始比较。比较的方式如下：

1. 如果arr[j]比arr[i]原始值小，我们将arr[j]复制到arr[j+1]处，同时j自动减一
2. 如果arr[j]比arr[i]原始值大，由于前面的牌已经是从大到小的顺序，因此这个位置一定是我们想要的插入arr[i]原始值的位置。

代码实现

func insertionSort(a []int, opt SortOption) []int {
	for i := 1; i < len(a); i++ {
		tmp := a[i]
		j := i - 1
		for j >= 0 && a[j] < tmp {
			a[j+1] = a[j]
			j--
		}
		a[j+1] = tmp
	}
	return a
}
1
2
3
4
5
6
7
8
9
10
11
12

快速排序(quick sort)

问题分析

上述算法复杂度均为$O(n^2)$，接下来我们介绍一种更快的排序方法——快速排序：
对于函数quick_sort(arr, left, right)

1. 取arr的第一个元素，使其归位(partition)，即让第一个元素提前到达最终它应该在的位置。
2. 将arr分成两个部分：比第一个元素大的部分和比第一个元素小的部分；
3. 递归地解决这两个部分。
   代码逻辑大体如下：

func quickSort(arr []int, left, right int) []int {
	if left < right {
		mid = partition(arr, left, right)
		quickSort(arr, mid + 1 , right)
		quickSort(arr, left, mid - 1)
	}
	return arr
}
1
2
3
4
5
6
7
8

其中left是我们考察区间的最左侧位置，right同理。那么归位函数partition(arr, left, right)应该如何实现呢？
首先把arr的第一个元素单独拿出来作为head，此时left指向了一个空位！因此我们移动right，直到找到一个比head小的元素arr[right]，将其复制到arr[left]处。接下来开始移动left，直到找到一个比head大的元素arr[left]，将其复制到arr[right]处。
注意在上述过程中，我们再次用到了“空位”和“复制”的概念，而空位就是通过逐对复制元素实现的，这和插入排序不谋而合。

代码实现

func partition(a *[]int, left, right int, opt SortOption) int {
	head := (*a)[left]
	for left < right {
		for left < right && *a)[right] <= head {
			// 找出比head小的数
			right-- //右指针向左移动一位
		}
		(*a)[left] = (*a)[right] // 把右边的值放到左边空位
		for left < right && *a)[left] >= head {
			// 找出比head大的数
			left++ //左指针向右移动一位
		}
		(*a)[right] = (*a)[left] // 把右边的值放到左边空位
	}
	(*a)[left] = head // 把head归位
	return left
}

func quickSort(a *[]int, left, right int) []int {
	if left < right {
		mid := partition(a, left, right)
		quickSort(a, left, mid-1)
		quickSort(a, mid+1, right)
	}
	return *a
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

今日Leetcode

问题描述

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

代码实现

暴力实现

思路太简单：

func twoSum(nums []int, target int) []int {
    for k1, v1 := range nums {
        for k2, v2 := range nums {
            if k1 != k2 && v1 + v2 == target {
                return []int{k1, k2}
            }
        }
    }
    return []int{}
}
1
2
3
4
5
6
7
8
9
10

哈希表实现

上述方式耗时太久，主要原因在于寻找target-num花了太长时间（或者说出现了太多重复查找），因此我们可以引入哈希表来缩短查找时间。

func twoSum(nums []int, target int) []int {
    helpMap := make(map[int]int) // value -> index
    for i, num := range nums {
        if j, ok := helpMap[target - num]; ok {
            return []int{i, j}
        }
        helpMap[num] = i
    }
    return []int{}
}
1
2
3
4
5
6
7
8
9
10

参考资料

清华大学博士讲解Python数据结构与算法
用二进制来解汉诺塔问题