快速排序（三种方法实现）

1. 快速排序

(1)思想
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

<1>hoare法（左右指针法）

(1)画图理解
取最左边key为基准值，用right指针找比key值小的元素，用left指针找比key位置大的元素，将两位置值进行交换，最后，将key值放在二者相遇位置上，就可保证key左边都是比key小的值，右边都是比key大的值，然后进行递归即可实现，从相遇点分割成两部分，在分别对左右两部分重复上述排序。

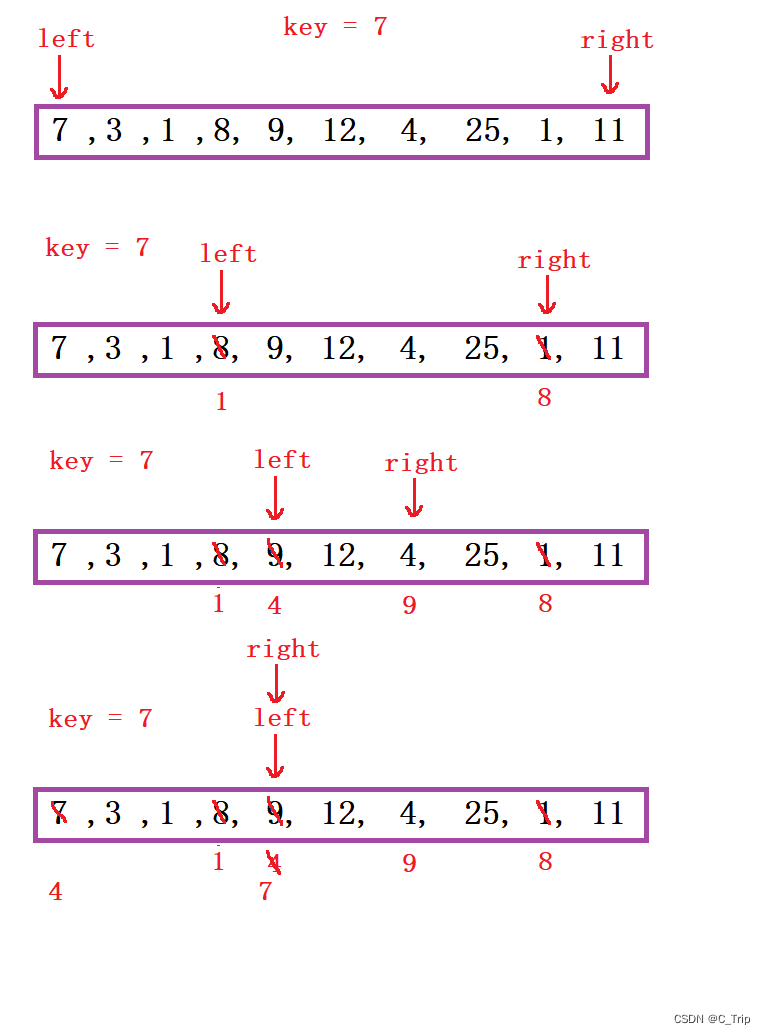
(2) 代码思路

//-----------------------快排-------------------/
int HoareSort(int* a, int begain, int end)
{
	int key = begain;
	int left = begain, right = end;
	while (left < right)
	{
		//右边找比key小的值
		while (left < right && a[right] >= a[key])
			right--;
		//左边找比key大的值
		while (left < right && a[left] <= a[key])
			left++;
		swap(&a[right], &a[left]);
	}
	int meeti = left;
	swap(&a[meeti], &a[key]);
	return meeti;
}
void QuickSort(int* a, int begain, int end)
{
	//递归返回条件如果该区间只有一个值或没有值则返回
	if (begain >= end)
		return;
	int meeti = HoareSort(a, begain, end);
	QuickSort(a, begain, meeti - 1);
	QuickSort(a, meeti + 1, end);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

<2>挖坑法

(1)画图理解
思路：取最左边或最右边值做key，右边形成一个坑，定义两个指针left、right指向头和尾。右边找小值放到左边坑中右边形成新坑，左边找大值放到右边左边形成新坑，将key放到相遇位置。这时key左边值均小于key，右边值均大于key。

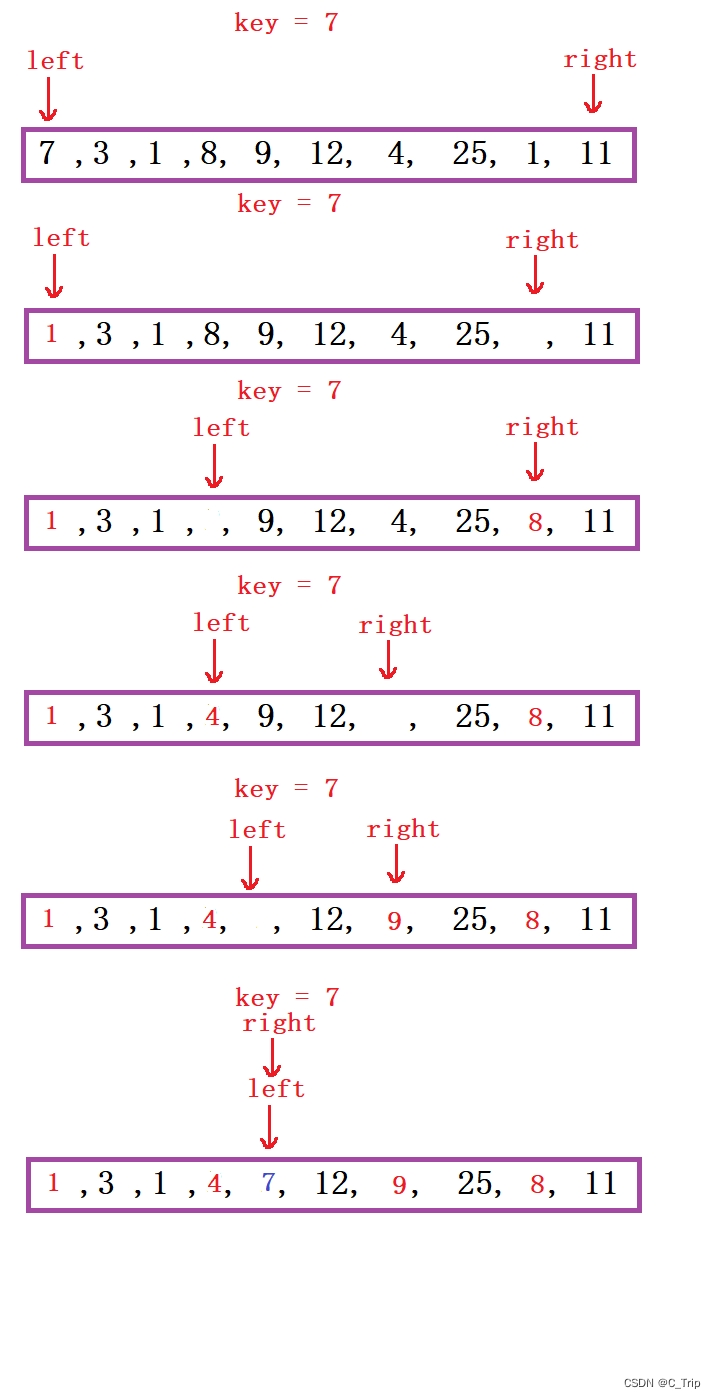
(2) 代码思路

//挖坑法
int DigHoleSort(int* a, int begain, int end)
{
	int key = a[begain];
	int left = begain, right = end;
	while (left < right)
	{
		//右边找小值
		while (left < right && a[right] >= key)
			right--;
		//放到左边坑位中，右边形成新的坑
		a[left] = a[right];
		
		//左边找大值
		while (left < right && a[left] <= key)
			left++;
		//放到右边坑位中，左边形成新的坑
		a[right] = a[left];
	}
	int meeti = left;
	a[meeti] = key;
	return left;
}
void QuickSort(int* a, int begain, int end)
{
	if (begain >= end)
		return;
	//int meeti = HoareSort(a, begain, end);
	int meeti = DigHoleSort(a, begain, end);
	QuickSort(a, begain, meeti - 1);
	QuickSort(a, meeti + 1, end);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

<3>前后指针法

(1)画图理解
定义两指针一前一后，cur指针找比key小的值，和prev指针前一个值进行交换，直至结束。将prev位置值与key位置值进行交换，此时key位置值，左边比key位置值小，右边比key位置值大，在进行分治就可以了。

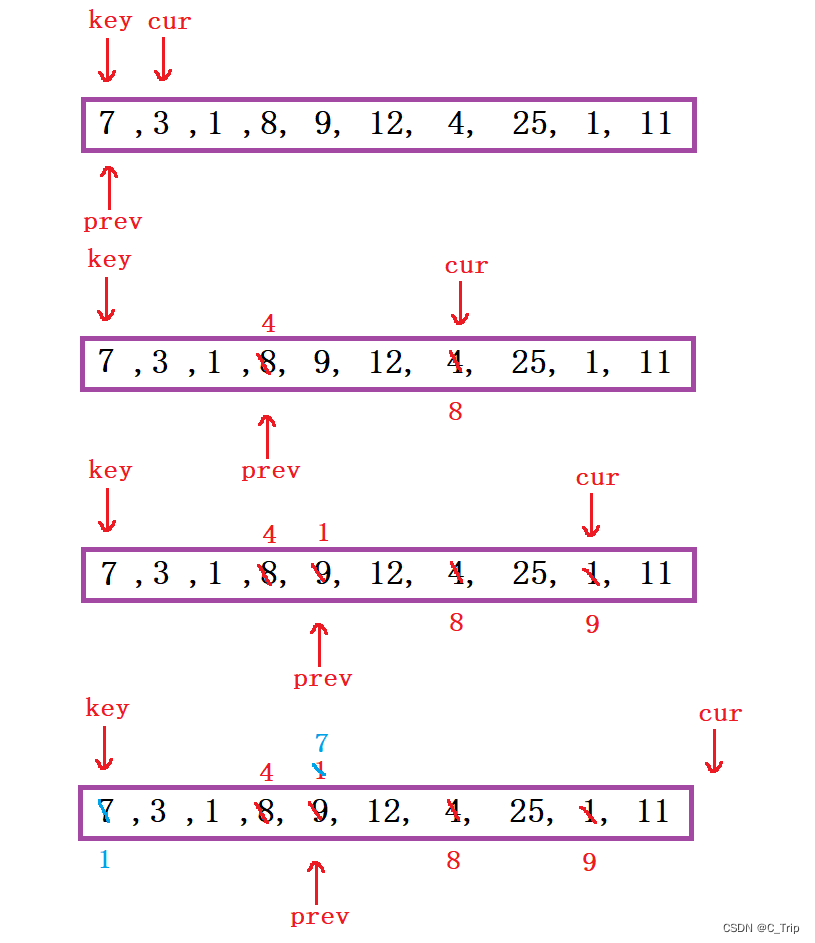
(2) 代码思路

int PBIndexSort(int* a, int begain, int end)
{
	int key = begain;
	//定义两个指针，一前一后
	int prev = begain, cur = begain + 1;
	while (cur <= end)
	{
		//如果cur位置值比key小则与perv前一个值进行交换
		if (a[cur] < a[key] && ++prev != cur)
		{
			swap( &a[cur], &a[prev] );
		}
		cur++;
	}
	//将key放在prev位置
	swap(&a[prev], &a[begain]);
	return prev;
}
void QuickSort(int* a, int begain, int end)
{
	if (begain >= end)
		return;
	//int meeti = HoareSort(a, begain, end);
	//int meeti = DigHoleSort(a, begain, end);
	int meeti = PBIndexSort(a, begain, end);
	QuickSort(a, begain, meeti - 1);
	QuickSort(a, meeti + 1, end);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

总结
三种方法最终目的都是为了让，key放到它应该排序的位置同时，key左边的值都比key小，key右边的值都比key大，然后进行分治就可以了。

<4>快速排序优化

(1)三数取中法取key
理想情况下我们每回选的key位置值都近似为数组中位数，这样每回递归都为二分。但当数据出现极端情况时，会使我们的快速排序效率大打折扣例如

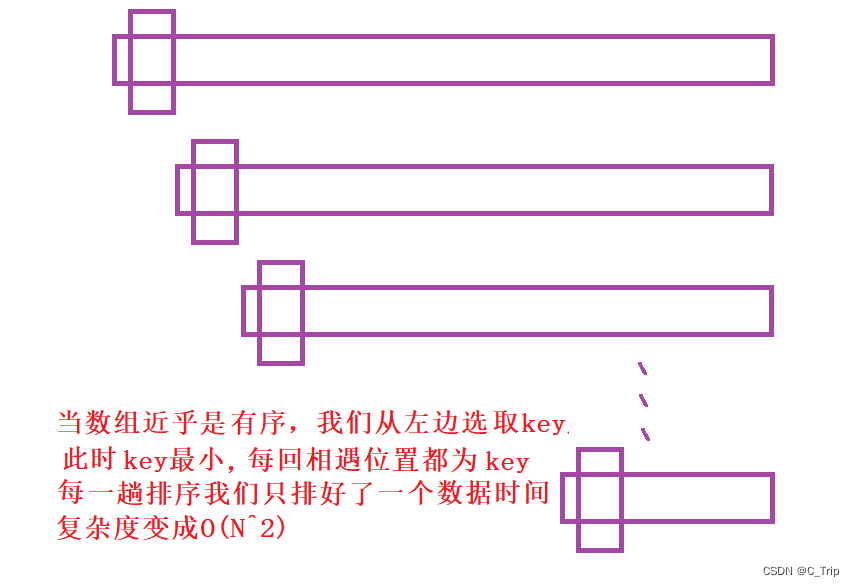
优化代码
以hoare法为例

//三数取中法
int GetMidIndex(int* a, int left, int right)
{
	int mid = (left + right) >> 1;
	if (a[mid] > a[left])
	{
		if (a[mid] < a[right])
			return mid;
		else if (a[left] < a[right])
			return right;
		else
			return left;
	}
	else
	{
		if (a[mid] > a[right])
			return mid;
		else if (a[left] < a[right])
			return left;
		else
			return right;
	}
}
//hoare法（左右指针法）
int HoareSort(int* a, int begain, int end)
{
	int mid = GetMidIndex(a, begain, end);
	swap(&a[mid], &a[begain]);
	
	//这里我们仍然取key为最左边的数，只不过最左边的值变了
	int key = begain;
	int left = begain, right = end;
	while (left < right)
	{
		//右边找比key小的值
		while (left < right && a[right] >= a[key])
			right--;
		//左边找比key大的值
		while (left < right && a[left] <= a[key])
			left++;
		swap(&a[right], &a[left]);
	}
	int meeti = left;
	swap(&a[meeti], &a[key]);
	return meeti;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

(2)小区间优化法
小区间优化法实际上就是减少递归的深度，以此来提升效率代码如下：

void QuickSort(int* a, int begain, int end)
{
	if (begain >= end)
		return;
 
	//小区间优化法 当数据量比较大的时候可以通过调整参数(20),来减小递归次数，提高性能
	if ((end - begain) > 20)
	{
		int meeti = HoareSort(a, begain, end);
		QuickSort(a, begain, meeti - 1);
		QuickSort(a, meeti + 1, end);
	}
	else
	{
		//数量比较少的时候用直接插入来排序
		InsertSort(a + begain, end - begain + 1);
	}
 
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

<5>非递归实现

利用栈来存储区间下标，代码如下：要注意先数组头，后入数组尾。出栈时栈顶的数据为数组尾，在出才为头位置下标。代码如下：

void QuickSortNonR(int* a, int begain,  int end)
{
	Stack st;
	StackInit(&st);
	//入栈
	StackPush(&st, begain);
	StackPush(&st, end);
	while (!StackEmpty(&st))
	{
		//出栈
		int right = StackTop(&st);
		StackPop(&st);
		int left = StackTop(&st);
		StackPop(&st);
		//单趟排序
		int mid = HoareSort(a, left, right);
		if (left < mid - 1)
		{
			StackPush(&st, left);
			StackPush(&st, mid - 1);
		}
		if (mid + 1 < right)
		{
			StackPush(&st, mid + 1);
			StackPush(&st, right);
		}
	}
	StackDestory(&st);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

2.特性

1、快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
2、时间复杂度：O(N*logN)