函数递归（Recursion）一篇便懂_定义一个递归函数recursive_function,函数名为recursive_function,

递归的概念

在 C 语言中，递归（Recursion）是一种函数调用自身的编程技术。当一个函数在其定义中调用自身时，就称为递归函数。

• 了解递归思想

把⼀个大型复杂问题层层转化为⼀个与原问题相似，但规模较小的子问题来求解；直到子问题不能再 被拆分，递归就结束了。所以递归的思考方式就是把大事化小的过程。 递归中的递就是递推的意思，归就是回归的意思，接下来慢慢来体会

• 递归的两个重要条件

递归在书写的时候，有2个必要条件：  

一、递归存在限制条件，当满足这个限制条件的时候，递归便不再继续。

二、每次递归调⽤之后越来越接近这个限制条件。 

---

递归举例

我们先看一个简单例子 

int function(int n)
{
	if(n==0)
	{
		//递归终止条件
		return 1;
	}
	else
	{
			//递归调用
		return function(n - 1) * 2;
	}
}
 
int main() {
	int num = 5;
	int ret =function(num);
	printf("%d\n",ret);
	return 0;
}

在上述示例中， recursiveFunction  是一个递归函数。它接受一个整数参数  n ，并根据  n  的值来计算结果。
 
- 当  n  等于 0 时，递归终止，并返回 1。

- 否则，它会调用自身，将  n  减 1，并将结果乘以 2。
 
通过这种方式，递归函数可以逐步缩小问题的规模，直到达到终止条件。
 
递归在处理一些问题时非常有用，例如斐波那契数列、树的遍历等。但需要注意的是，递归函数在递归深度过大时可能会导致栈溢出，并且递归的实现可能比迭代更消耗内存。

---

例一、  这次我们运用这个简单逻辑的题目来了解递归，求n！。

            如，3！=3*2*1=6。

#include<stdio.h>
int fact(static n)
{
	if (n == 0)
	{
		return 1;
 
	}
	else
	{
 
		return n * fact(n - 1);
	}
 
 
}
 
 
 
int main()
{
	int n = 0;
	int ret = 0;
	sacnf("%d", &n);
	ret = fact(n);
	printf("%d/n", ret);
	return 0;
 
 
}

通过代码我们看到 fact函数比较简洁，这也算是递归的特点，虽然代码简洁但需要注意的是他的逻辑可不简单。首先我们先分析一下n！=n*（n-1）！以此下去再算n-1的阶乘再再算n-1-1的阶乘······再往后就省略了。然后两个限制条件，其中一个便是if（n==0），另一个是当不断递推下去时n不断减1，所以越开越接近条件n==1，这就是第二个条件。

现在我们来了解剖上面说的以及递推和回归了，为了便于理解，我们要看图了解

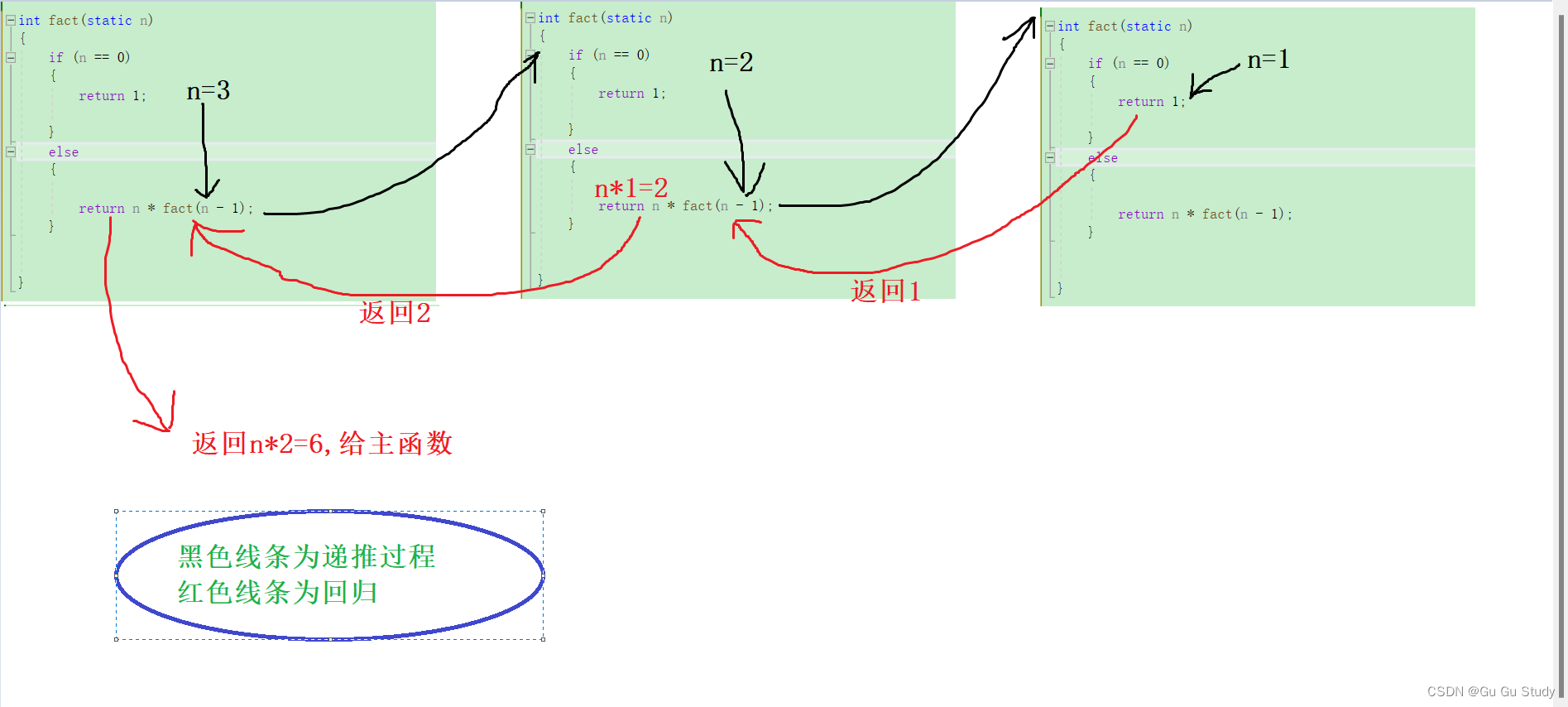
通过图片里我也写出了，黑线为递推过程，红色为回归过程，

总的来说递归有两条件，两过程，这些便是递归的主要内容，且有些情况下递归解决问题可能会比较繁琐，效率较低，接下来会为大家一一说明。

---

 

例二、

          顺序打印⼀个整数的每⼀位，如：输入7680，输出7 6 8 0

这时我们也可以用递归来解决这个问题，代码如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void function(int n)
{
	
		if (n > 9)
		{
			function(n / 10);
		}
		printf("%d ", n % 10);
 
	
 
}
 
 
int main()
{
	int n = 0;
	scanf("%d", &n);
	function(n);
 
	return 0;
}

 

---

不难发现这个代码也很明显的展示出两个条件，if（n>9），以及不断递推后越来越接近第一个条件，接下来我们再借助图来解剖这个代码和递归逻辑。

这个图解依然是黑色为递推，红色为回归 

这么一看图我们是不是就对递归的过程一清二楚了呢，代码先是以n=7680，进入第一个function函数，之后符合if语句条件，继续调用function，也就是递归，之后再继续······，到了if语句不符合时开始进入回归状态，打印n%0.最后如图所示依次打印7 6 8 0

下面讲一下运用递归知识解决的典型问题，汉诺塔文体，虽然我之前已经发过作品了，但现在还是搬过来看一下吧。

汉诺塔

汉诺塔又称河内塔，起源于印度，传说大反天创造世界时做了三根金刚石柱，其中一根柱子上落着六十四片黄金圆盘。大反天命令陀螺门将圆盘按大小顺序重新摆放到另一根柱子上，规定每次只能移动一块，并且大圆盘不能放到小圆。

#include<stdio.h>
int count;
void move(char a, char b, char c, int n)
{
	if (n == 1)
	{
		++count;
		printf("第%d次移动：将现在%c上的第一个圆盘移到%c\n",count,a,c);
	}
	else if (n > 1)
	{
		move(a, c, b, n - 1);//通过c柱子将a柱子上n-1个圆盘移到b
		++count;
		printf("第%d次移动：将现在%c上的第一个圆盘移到%c\n",count, a, c);
		move(b, a, c, n - 1);//看下文绿色字体解释
	}
}
 
int main()
{
	int n;
	scanf("%d", &n);
	move('a','b','c', n);
	return 0;
 
}

 

现在我们看下图进行解析： 

 

 

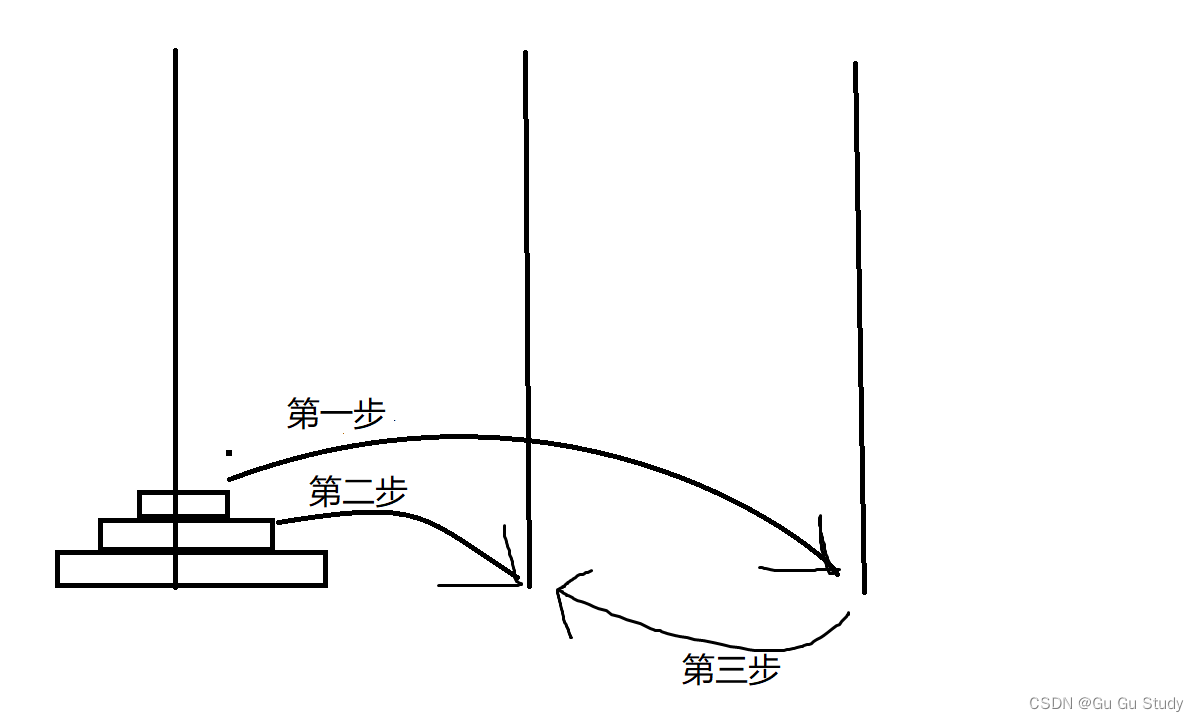
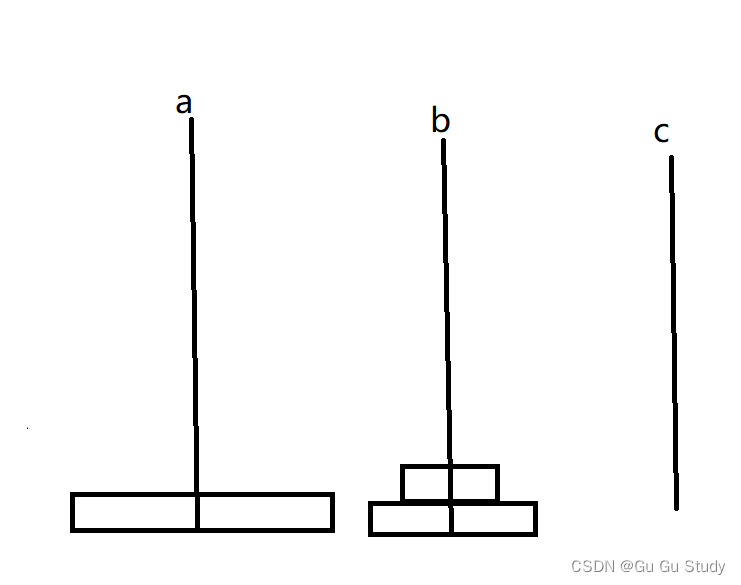
经过这样移动便可将n-1个圆盘移动到b上，这个过程通过代码实现便是上面的：

move(a, c, b, n - 1);

然后将a上最后一个圆盘移到。然后得到下图：

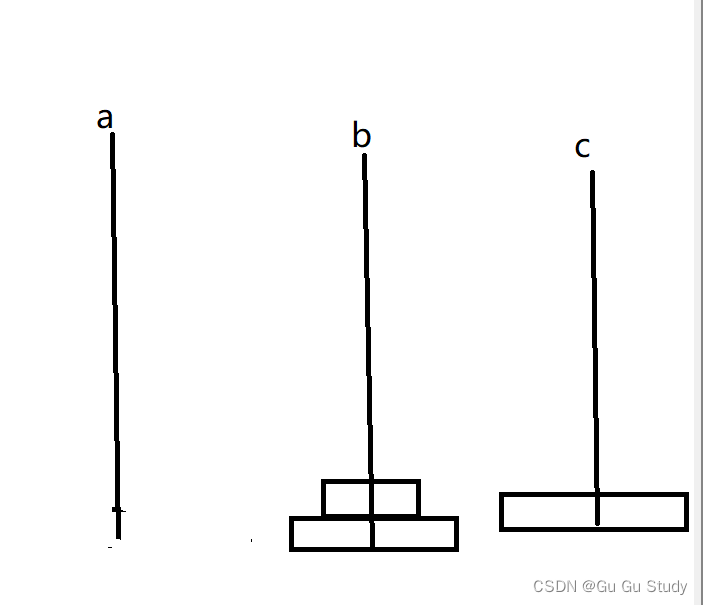
这时我们发现a是空的，b是有2个圆盘，c上有一个最大的圆盘因为其不影响任何其他圆盘放在c上所以我们可以假设c没有圆盘，如果我们把a当作b，b当作a是不是就相当于刚开始n为2个圆盘，故此我们在调用一次函数即递归，代码实现便是move(b, a, c, n - 1);至此函数不断递归下去直到

n-1为1时函数结束！！！这便是递归解决汉诺塔问题了！！！

 

---

递归与迭代

迭代又是什么呢?与递归又有什么区别呢。

现在我们以求阶乘的问题来用代码形式展示迭代与递归的关系

递归求阶乘

#include<stdio.h>
int fact(static n)
{
	if (n == 0)
	{
		return 1;
 
	}
	else
	{
 
		return n * fact(n - 1);
	}
 
 
}
 
 
 
int main()
{
	int n = 0;
	int ret = 0;
	sacnf("%d", &n);
	ret = fact(n);
	printf("%d/n", ret);
	return 0;
 
 
}

---

 

迭代求阶乘

int main()
{
	int n = 0;
	int ret = 1;
	scanf("%d", &n);
	while (n > 0)
	{
		ret *= n;
		n--;
	}
	printf("%d", ret);
	return 0;
}

上面两端代码已经很清楚展示诋毁与迭代的区别了。

在 C 语言中，递归和迭代是两种不同的循环方式，它们之间存在以下关系：
 
1. 递归是一种通过自身不断调用自身来实现循环的方法。在递归中，函数在执行过程中会调用自身，并将问题规模逐渐减小，直到达到终止条件。例如，计算斐波那契数列可以使用递归实现。

2. 迭代是一种使用循环语句（如 for、while）来重复执行一段代码的方法。在迭代中，代码会根据循环条件不断执行，直到达到终止条件。例如，计算累加和可以使用迭代实现。

3. 递归和迭代可以相互转换。有些问题可以使用递归或迭代来解决，具体取决于问题的特性和编程者的偏好。例如，计算阶乘可以使用递归或迭代实现。

4. 递归在处理树状结构和递归定义的问题时比较方便，而迭代在处理线性结构和需要提前知道循环次数的问题时比较方便。

5. 递归可能会导致栈溢出的问题，而迭代通常不会。在处理大规模数据时，迭代通常比递归更高效。
 
总之，递归和迭代是两种不同的循环方式，它们可以相互转换，各有优缺点，应根据具体情况选择合适的方法。
 

---

好了这篇文章就到这里了！