论文《Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts》_论文阅读modeling task relationships in multi-task lear

论文地址：https://dl.acm.org/doi/pdf/10.1145/3219819.3220007

摘要

常用的多任务学习往往对于任务之间的关系比较敏感，论文提出的MMoE将专家混合结构应用到多任务模型中，所有任务共享专家子模型，同时训练门控网络来优化每个任务。

Neural-based multi-task learning has been successfully used in many real-world large-scale applications such as recommendation systems. For example, in movie recommendations, beyond provid- ing users movies which they tend to purchase and watch, the system might also optimize for users liking the movies afterwards. With multi-task learning, we aim to build a single model that learns these multiple goals and tasks simultaneously. However, the prediction quality of commonly used multi-task models is often sensitive to the relationships between tasks. It is therefore important to study the modeling tradeoffs between task-specific objectives and inter-task relationships.
In this work, we propose a novel multi-task learning approach, Multi-gate Mixture-of-Experts (MMoE), which explicitly learns to model task relationships from data. We adapt the Mixture-of- Experts (MoE) structure to multi-task learning by sharing the expert submodels across all tasks, while also having a gating network trained to optimize each task. To validate our approach on data with different levels of task relatedness, we first apply it to a synthetic dataset where we control the task relatedness. We show that the proposed approach performs better than baseline methods when the tasks are less related. We also show that the MMoE structure results in an additional trainability benefit, depending on different levels of randomness in the training data and model initialization. Furthermore, we demonstrate the performance improvements by MMoE on real tasks including a binary classification benchmark, and a large-scale content recommendation system at Google.

简介

阐述背景，以电影推荐为例，不仅仅希望用户购买观看电影，而且希望用户对电影的评分较高，这样就有更多的后续消费。

In recent years, deep neural network models have been successfully applied in many real world large-scale applications, such as rec- ommendation systems [11]. Such recommendation systems often need to optimize multiple objectives at the same time. For example, when recommending movies for users to watch, we may want the users to not only purchase and watch the movies, but also to like the movies afterwards so that they’ll come back for more movies. That is, we can create models to predict both users’ purchases and their ratings simultaneously. Indeed, many large-scale recommen- dation systems have adopted multi-task learning using Deep Neural Network (DNN) models

之前有研究表明可以利用正则及迁移学习来实现多任务学习，但实际上数据分布差异、任务之间的差异对于多任务模型非常敏感，尤其是所有任务共享模型参数的时候。

Researchers have reported multi-task learning models can im- prove model predictions on all tasks by utilizing regularization and transfer learning [8]. However, in practice, multi-task learning models do not always outperform the corresponding single-task models on all tasks [23, 26]. In fact, many DNN-based multi-task learning models are sensitive to factors such as the data distribution differences and relationships among tasks [15, 34]. The inherent conflicts from task differences can actually harm the predictions of at least some of the tasks, particularly when model parameters are extensively shared among all tasks

以往研究是假设不同任务是由特定的数据分布产生的，根据这个假设来处理不同的任务，实际应用中数据模式非常复杂，很难度量不同任务间的差异。

Prior works [4, 6, 8] investigated task differences in multi-task learning by assuming particular data generation processes for each task, measuring task differences according to the assumption, and then making suggestions based on how different the tasks are. However, as real applications often have much more complicated data patterns, it is often difficult to measure task differences and to make use of the suggested approaches of these prior works.

最近研究是不依赖显式的任务差异度量，而是通过增加每个任务的模型参数来适应每个任务的不同。在大型推荐系统中有百万或者数十亿参数，增加的参数常常没有约束，可能对效果起反作用，而且在资源有限的情况下，新增的参数所需要的计算资源也无法实际应用。

Several recent works proposed novel modeling techniques to handle task differences in multi-task learning without relying on an explicit task difference measurement [15, 27, 34]. However, these techniques often involve adding many more model parameters per task to accommodate task differences. As large-scale recommenda- tion systems can contain millions or billions of parameters, those additional parameters are often under-constrained, which may hurt model quality. The additional computational cost of these param- eters are also often prohibitive in real production settings due to limited serving resource.

论文提出的MMoE显示建模任务间的关系和每个任务的目标，每个任务没有新增很多参数。
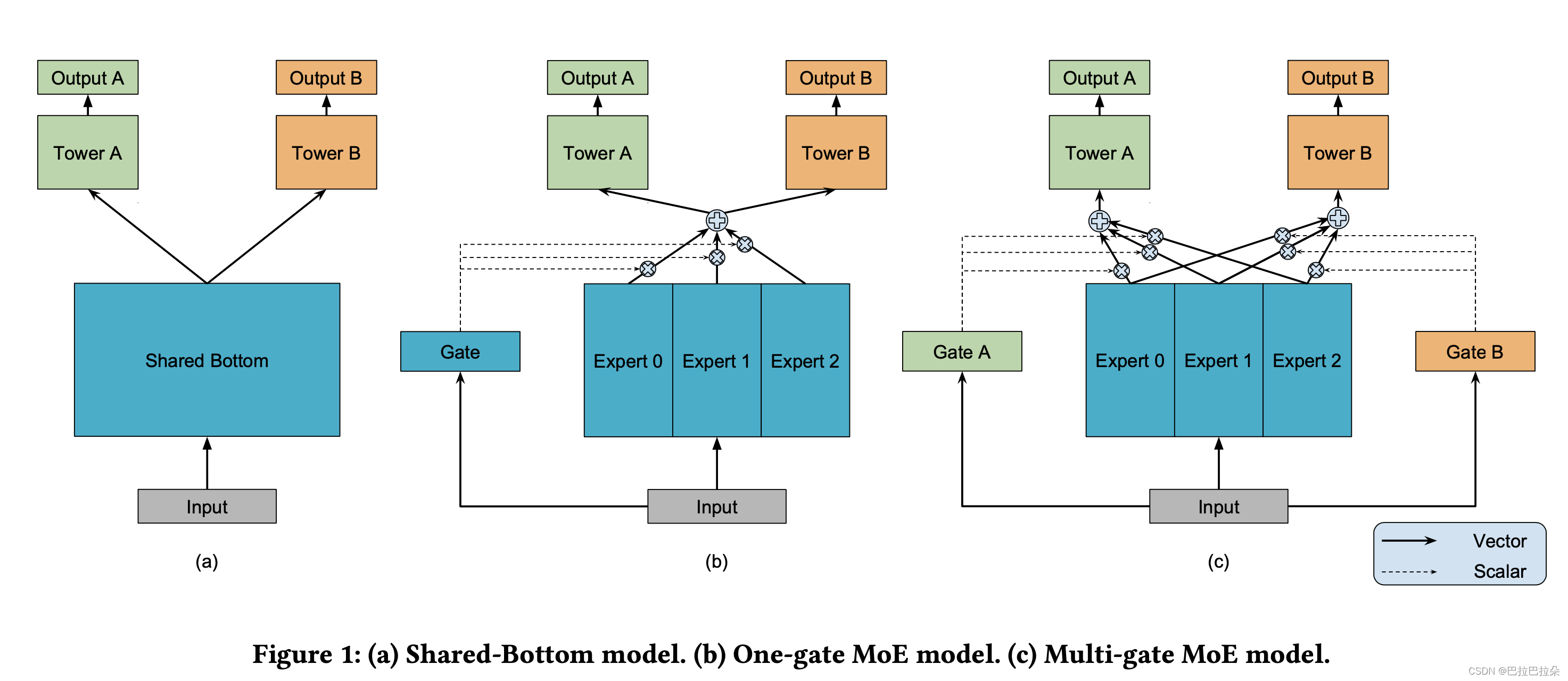
MMoE是基于底层共享结构MoE的（Figure 1a），MoE是所有任务都共享底层，各个任务上面有自己的输出塔，MMoE底层有多个专家结构，每个任务有个门控网络，通过输入特征及门控网络来差异化利用底层的专家网络，以此来捕捉任务间的关系。

In this paper, we propose a multi-task learning approach based on a novel Multi-gate Mixture-of-Experts (MMoE) structure, which is inspired by the Mixture-of-Experts (MoE) model [21] and the recent MoE layer [16, 31]. MMoE explicitly models the task rela- tionships and learns task-specific functionalities to leverage shared representations. It allows parameters to be automatically allocated to capture either shared task information or task-specific infor- mation, avoiding the need of adding many new parameters per task.
The backbone of MMoE is built upon the most commonly used Shared-Bottom multi-task DNN structure [8]. The Shared-Bottom model structure is shown in Figure 1 (a), where several bottom lay- ers following the input layer are shared across all the tasks and then each task has an individual “tower” of network on top of the bottom representations. Instead of having one bottom network shared by all tasks, our model, shown in Figure 1 ©, has a group of bottom networks, each of which is called an expert. In our paper, each expert is a feed-forward network. We then introduce a gating net- work for each task. The gating networks take the input features and output softmax gates assembling the experts with different weights, allowing different tasks to utilize experts differently. The results of the assembled experts are then passed into the task-specific tower networks. In this way, the gating networks for different tasks can learn different mixture patterns of experts assembling, and thus capture the task relationships.

探究MMoE怎样在多任务中学习专家网络及门控网络，论文利用皮尔逊系数来测量及控制任务之间的相关性，在数据生成中利用sin函数引入非线性来合成两个回归任务。任务相关性越低，MMoE更容易训练，这也和最近关于门控网络可以提升非凸神经网络结构的可训练性相关。

To understand how MMoE learns its experts and task gating net- works for different levels of task relatedness, we conduct a synthetic experiment where we can measure and control task relatedness by their Pearson correlation. Similar to [24], we use two synthetic regression tasks and use sinusoidal functions as the data generation mechanism to introduce non-linearity. Our approach outperforms baseline methods under this setup, especially when task correlation is low. In this set of experiments, we also discover that MMoE is easier to train and converges to a better loss during multiple runs. This relates to recent discoveries that modulation and gating mech- anisms can improve the trainability in training non-convex deep neural network

论文贡献有3点，第一，提出新的MMoE模型来建模任务间的关系，通过门控网络学习到共享信息和每个特定任务的信息。第二，利用合成的数据做对照实验，揭示MMoE如何提升模型的在不同任务相关性上的可训练性及可解释性。第三，在真实的大规模数据集上实验效果显著。

The contribution of this paper is threefold: First, we propose a novel Multi-gate Mixture-of-Experts model which explicitly models task relationships. Through modulation and gating networks, our model automatically adjusts parameterization between modeling shared information and modeling task-specific information. Second, we conduct control experiments on synthetic data. We report how task relatedness affects training dynamics in multi-task learning and how MMoE improves both model expressiveness and trainability. Finally, we conduct experiments on real benchmark data and a large-scale production recommendation system with hundreds of millions of users and items. Our experiments verify the efficiency and effectiveness of our proposed method in real-world settings

相关工作

DNN多任务学习

多任务模型可以学习到不同任务的共性及差异，广泛用到的是基于底层共享的多任务模型，这种网络结构减少了过拟合的风险，但是任务之间的差异会使优化变的困难，因为所有任务用的底层参数是一样的。

Multi-task models can learn commonalities and differences across different tasks. Doing so can result in both improved efficiency and model quality for each task [4, 8, 30]. One of the widely used multi-task learning models is proposed by Caruana [8, 9], which has a shared-bottom model structure, where the bottom hidden layers are shared across tasks. This structure substantially reduces the risk of overfitting, but can suffer from optimization conflicts caused by task differences, because all tasks need to use the same set of parameters on shared-bottom layers.

最近的一些研究在特定的任务的参数上面加约束，而不是在任务之间共享隐层和参数。例如，对两个任务的两组参数集上加L2约束，或者为每个任务学习一个特定的隐层embedding。和底层共享模型相比，这些方法增加了大量的参数，需要大量数据来训练，而且效果可能还不好。

To understand how task relatedness affects model quality, prior works used synthetic data generation and manipulated different types of task relatedness so as to evaluate the effectiveness of multi- task models [4–6, 8].
Instead of sharing hidden layers and same model parameters across tasks, some recent approaches add different types of con- straints on task-specific parameters [15, 27, 34]. For example, for two tasks, Duong et al. [15] adds L-2 constraints between the two sets of parameters. The cross-stitch network [27] learns a unique combination of task-specific hidden-layer embeddings for each task. Yang et al. [34] uses a tensor factorization model to generate hidden-layer parameters for each task. Compared to shared-bottom models, these approaches have more task-specific parameters and can achieve better performance when task differences lead to con- flicts in updating shared parameters. However, the larger number of task-specific parameters require more training data to fit and may not be efficient in large-scale models.

子网络集成 & MoE

MoE层通过训练或者在线服务时的输入层来选择子网络，通入引入稀疏性来降低计算成本。以有多层且每层有多个子网络结构的大型网络结构PathNet为例，训练时会随机选择多个路径并行训练，确定最佳路径后选择新路径来训练新任务。MMoE也是借鉴它使用多个子网络的集成来实现迁移学习和减少计算。

In this paper, we apply some recent findings in deep learning such as parameter modulation and ensemble method to model task rela- tionships for multi-task learning. In DNNs, ensemble models and ensemble of subnetworks have been proven to be able to improve model performance [9, 20].
Eigen et al [16] and Shazeer et al [31] turn the mixture-of-experts model into basic building blocks (MoE layer) and stack them in a DNN. The MoE layer selects subnets (experts) based on the in- put of the layer at both training time and serving time. Therefore, this model is not only more powerful in modeling but also lowers computation cost by introducing sparsity into the gating networks. Similarly, PathNet [17], which is designed for artificial general in- telligence to handle different tasks, is a huge neural network with multiple layers and multiple submodules within each layer. While training for one task, multiple pathways are randomly selected and trained by different workers in parallel. The parameters of the best pathway is fixed and new pathways are selected for training new tasks. We took inspiration from these works by using an ensem- ble of subnets (experts) to achieve transfer learning while saving computation.

预备工作

底层共享多任务模型（MoE）

MoE包含一个底层共享的网络结构，表示为函数$f$，和$K$个塔网络，表示为$h^k$,$k=1,2,...,K$，每个任务的输出$y_k$可以表示为
$$y_k=h^k(f(x))(1)$$

We first introduce the shared-bottom multi-task model in Figure 1 (a), which is a framework proposed by Rich Caruana [8] and widely adopted in many multi-task learning applications [18, 29]. Therefore, we treat it as a representative baseline approach in multi- task modeling.
Given K tasks, the model consists of a shared-bottom network, k
represented as function f , and K tower networks h , where k = 1, 2, …, K for each task respectively. The shared-bottom network follows the input layer, and the tower networks are built upon the output of the shared-bottom. Then individual output $y_k$ for each task follows the corresponding task-specific tower. For task k, the model can be formulated as

产生人工合成数据

之前研究表明多任务学习模型取决于任务的相关性，不过实际应用中很那直接学习多个任务之间的相关性对模型的影响，因为实际应用召回多个任务之间的相关性没法改变。因此首先需要建一个可衡量可控制任务相关性的数据集。

Prior works [15, 27] indicate that the performance of multi-task learning models highly depends on the inherent task relatedness in the data. It is however difficult to study directly how task relat- edness affects multi-task models in real applications, since in real applications we cannot easily change the relatedness between tasks and observe the effect. Therefore to establish an empirical study for this relationship, we first use synthetic data where we can easily measure and control the task relatedness.
Inspired by Kang et al. [24], we generate two regression tasks and use the Pearson correlation of the labels of these two tasks as the quantitative indicator of task relationships. Since we focus on DNN models, instead of the linear functions used in [24], we set the regression model as a combination of sinusoidal functions as used in [33]. Specifically, we generate the synthetic data as follows

下面分5步来建立
step 1：假设输入特征向量维度为$d$，产生两个单位正交向量$u_1$,$u_2\in R^d$,
$$u_1^T{u}_2=0,||u_1||=1,||u_2||=1$$
step2：给定常量$c$和相关性分数$-1\le p\le 1$,产生两个权重向量$w_1$,$w_2$，使得
$$w_1=c{u}_1,w_2=c(p{u}_1+\sqrt{1-p^2}{u}_2)(2)$$
step3：从服从正态分布中随机抽样，$x\in R^d$,$N(0,1)$
step4：得到两个回归任务的label，$y_1$，$y_2$
$$y_1=w_1^{T}x+\sum _{i=1}^{m}sin({\alpha }_i{w}_1^{T}x+{\beta }_i)+{ϵ}_1(3)$$
$$y_2=w_2^{T}x+\sum _{i=1}^{m}sin({\alpha }_i{w}_2^{T}x+{\beta }_i)+{ϵ}_2(4)$$
这里${\alpha }_i,{\beta }_i$是控制$sin$函数的形状，${ϵ}_1,{ϵ}_2\sim N(0,0.1)$
step5：重复step3和step4直到产生足够数据

对于如果是线性场景，如下，两个labe$y_1,y_2$的皮尔逊相关系数就是$p$,
$$y_1=w_1^{T}x+{ϵ}_1$$
$$y_2=w_2^{T}x+{ϵ}_2$$
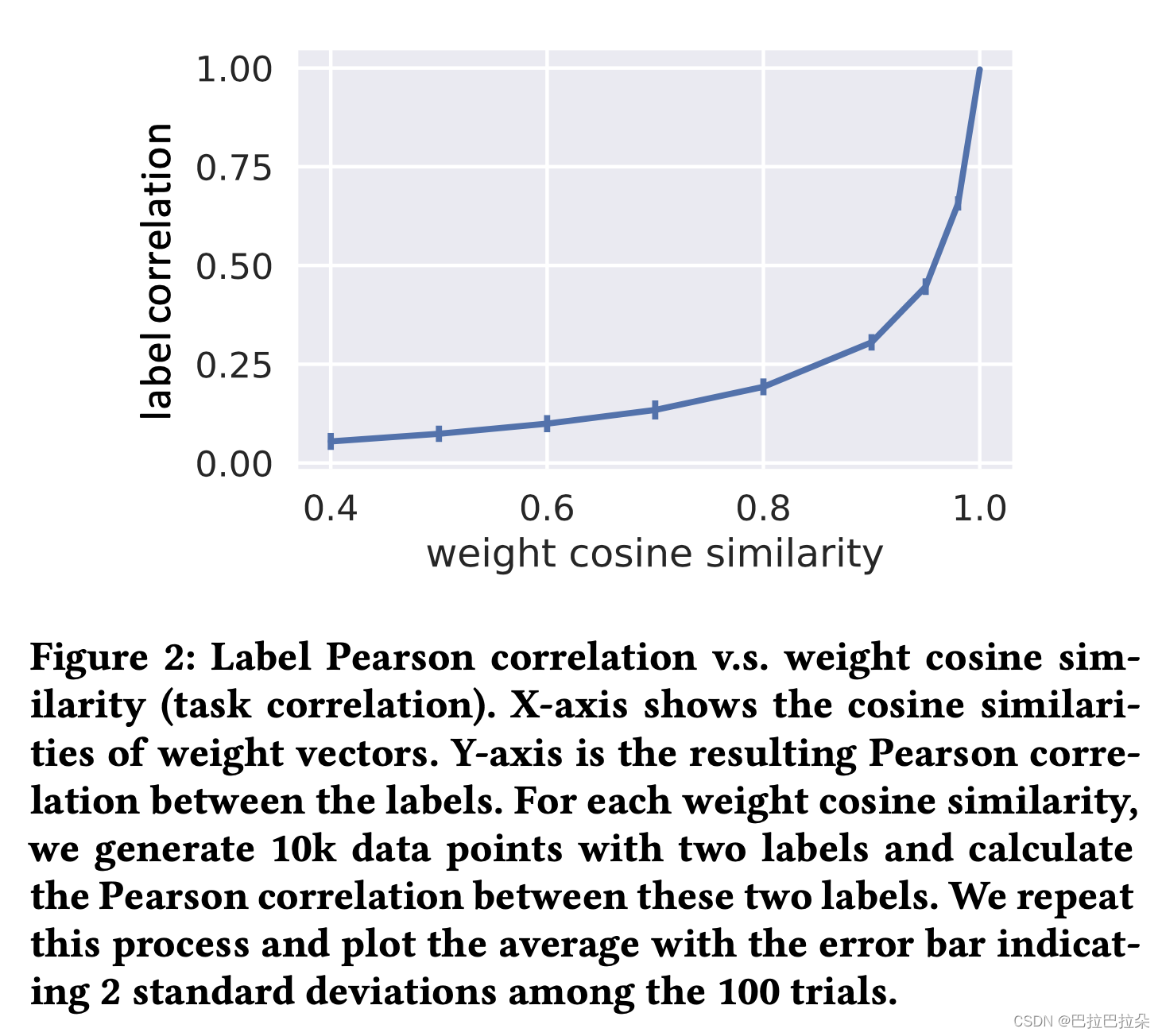
但是现在是非线性产生的数据，这个时候从权重向量的设计上面可以看到，有$cos(w_1,w_2)=p$,对于非线性情况，$y_1$和$y_2$也是正相关的，关系如下图（Figure 2）。
论文后面均以两个权重向量的相似度来描述任务相关性。

任务相关性的影响

为证实任务相关性对多任务模型的影响，进行如下实验
step 1：给定一系列相关性分数，每个分数产生一个合成的数据集
step 2：每个数据集训练一个底层共享的多任务模型，保持超参数一致
step 3：重复step1和step2几百次，保持相关性分数和网络的超参数不变
step 4：对每个不同的相关性的多任务计算平均性能指标

To verify that low task relatedness hurts model quality in a baseline multi-task model setup, we conduct control experiments on the synthetic data as follows.
(1) Given a list of task correlation scores, generate a synthetic dataset for each score;
(2) Train one Shared-Bottom multi-task model on each of these datasets respectively while controlling all the model and training hyper-parameters to remain the same;
(3) Repeat step (1) and (2) hundreds of times with datasets gen- erated independently but control the list of task correlation scores and the hyper-parameters the same;
(4) Calculate the average performance of the models for each task correlation score.

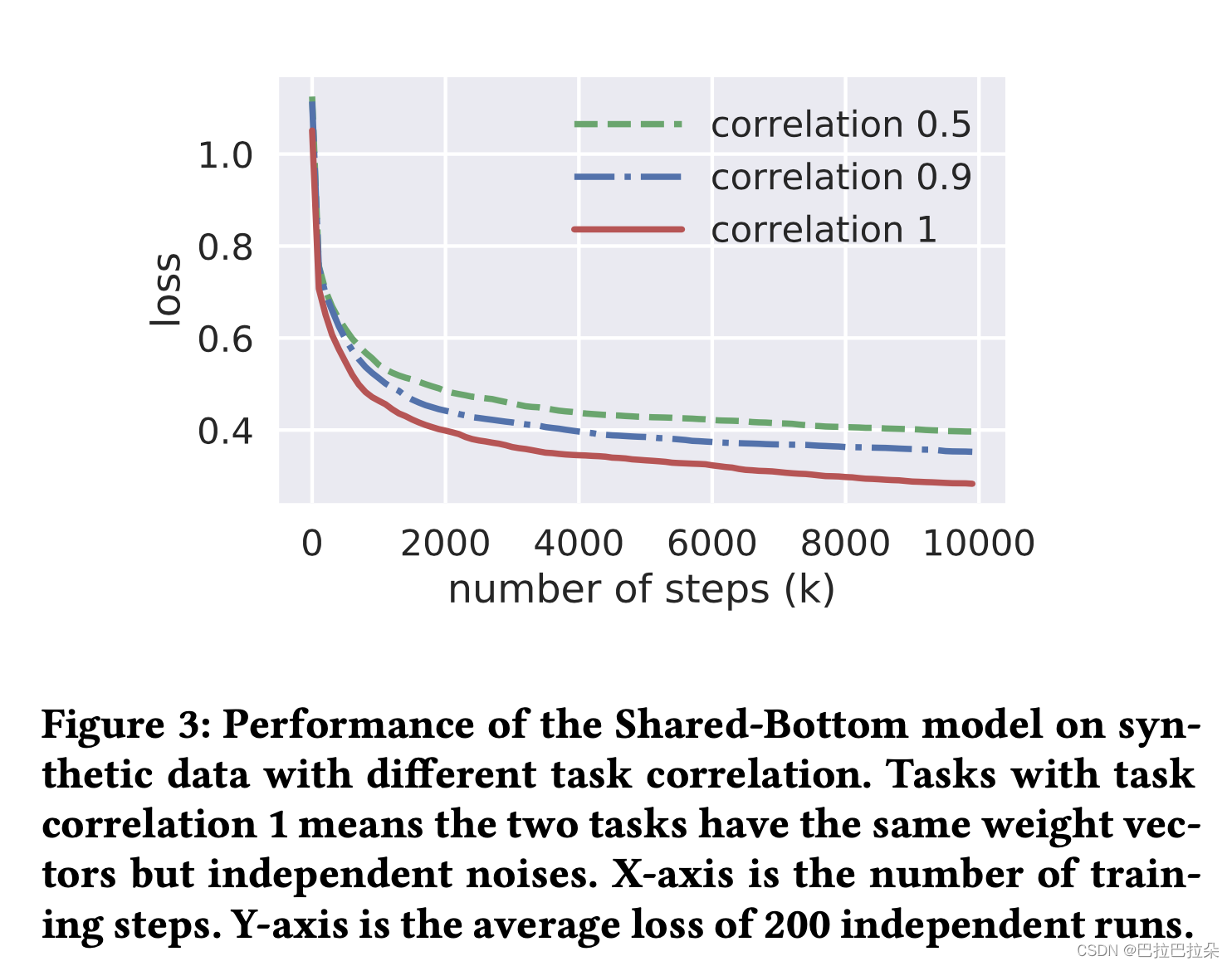
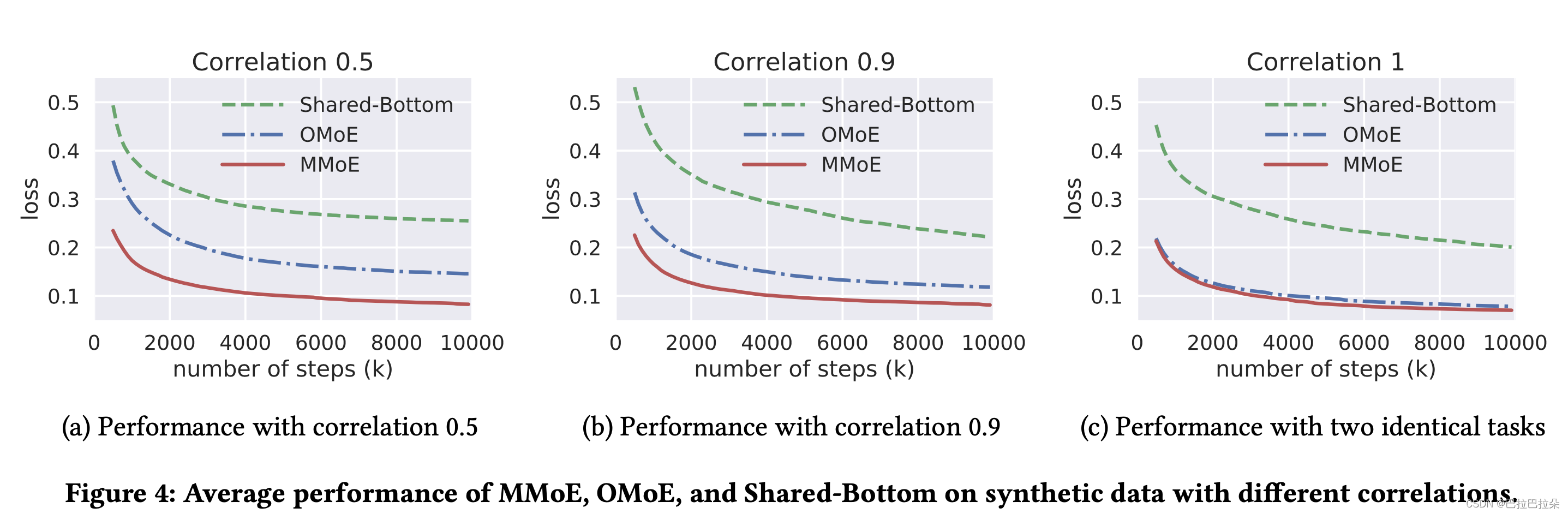
如图（Figure 3）所示，相关性越低，效果越差，因为是对称的两个任务，这个图仅绘制了一个任务的loss曲线，结果验证了多任务模型对任务相关性非常敏感的假设。

Figure 3 shows the loss curves for different task correlations. As expected, the performance of the model trends down as the task correlation decreases. This trend is general for many different hyper-parameter settings. Here we only show an example of the control experiment results in Figure 3. In this example, each tower network is a single-layer neural network with 8 hidden units, and the shared bottom network is a single-layer network with size=16. The model is implemented using TensorFlow [1] and trained using Adam optimizer [25] with the default setting. Note that the two regression tasks are symmetric so it’s sufficient to report the results on one task. This phenomenon validates our hypothesis that the traditional multi-task model is sensitive to the task relationships

建模思路

MoE

原始的MoE模型表示如下
$$y=\sum _{i=1}^{n}g(x{)}_i{f}_i(x)(5)$$
这里${\sum }_{i=1}^{n}g(x{)}_i=1$这里$g(x{)}_i$是输出$g(x)$的第$i$个logit，表示的是专家网络$f_i$的概率。$g$表示将所有的专家网络的集成起来的门控网络，门控网络具体是产生$n$个专家上面的一个数据分布，最终输出就是各个专家的一个加权结果。

MoE Layer：MoE模型一开始是个单独的模型，后面发展为一个基本的网络结构，可以将MoE堆叠在DNN中，MoE Layer表示这个层和MoE结构相同，将前一层的输出作为它的输入，MoE Layer的输出作为后续层的输入。

MoE Layer : While MoE was first developed as an ensemble method of multiple individual models, Eigen et al [16] and Shazeer et al [31] turn it into basic building blocks (MoE layer) and stack them in a DNN. The MoE layer has the same structure as the MoE model but accepts the output of the previous layer as input and outputs to a successive layer. The whole model is then trained in an end-to-end way.

MMoE

MMoE是用来设计为不用加很多新参数的情况下捕获任务差异性。和MoE一样，底层$f$共享，另外更重要的是为每一个任务$k$加了一个门控网络$g^k$。

We propose a new MoE model that is designed to capture the task differences without requiring significantly more model parameters compared to the shared-bottom multi-task model. The new model is called Multi-gate Mixture-of-Experts (MMoE) model, where the key idea is to substitute the shared bottom network f in Eq 1 with the MoE layer in Eq 5. More importantly, we add a separate gating network дk for each task k. More precisely, the output of task k is

$$y_k=h^k(f^k(x))(6)$$
$$f^k(x)=\sum _{i=1}^n{g}^k(x{)}_i{f}_i(x)(7)$$
门控网络计算如下：
$$g^k(x)=softmax(W_{gk}x)$$
$W_{gk}\in R^{n\times d}$,$n$是专家数量，$d$是特征维度。

Our implementation consists of identical multilayer perceptrons with ReLU activations. The gating networks are simply linear trans-
formations of the input with a softmax layer:

如果任务不怎么相关，共享的专家网络会受到惩罚，各个任务会利用不同的专家。先比MoE，MMoE只是增加了门控网络的参数。

Each gating network can learn to “select” a subset of experts to
use conditioned on the input example. This is desirable for a flexible parameter sharing in the multi-task learning situation. As a special case, if only one expert with the highest gate score is selected, each gating network actually linearly separates the input space into n regions with each region corresponding to an expert. The MMoE is able to model the task relationships in a sophisticated way by deciding how the separations resulted by different gates overlap with each other. If the tasks are less related, then sharing experts will be penalized and the gating networks of these tasks will learn to utilize different experts instead. Compared to the Shared-Bottom model, the MMoE only has several additional gating networks, and the number of model parameters in the gating network is negligible. Therefore the whole model still enjoys the benefit of knowledge transfer in multi-task learning as much as possible

所有任务共享一个门控网络称为OMoE，这样MoE、OMoE、MMoE就能串起来理解了。

To understand how introducing separate gating network for each task can help the model learn task-specific information, we compare with a model structure with all tasks sharing one gate. We call it One-gate Mixture-of-Experts (OMoE) model. This is a direct adaption of the MoE layer to the Shared-Bottom multi-task model. See Figure 1 (b) for an illustration of the model structure

MMoE在合成数据上面的表现

主要论证MMoE在任务不相关的情况下表现更好。

In this section, we want to understand if the MMoE model can in- deed better handle the situation where tasks are less related. Similar to Section 3.3, we conduct control experiments on the synthetic data to investigate this problem. We vary the task correlation of the synthetic data and observe how the behavior changes for dif- ferent models. We also conduct a trainability analysis and show that MoE based models can be more easily trained compared to Shared-Bottom models.

在不同相关性的合成数据上面表现

基线是MoE和OMoE，MMoE结构如下
结构如下：输入维度为100，和MoE一样，都有8个专家网络，每个专家网络是个单隐层网络，隐层节点数为16，上面的塔网络也是单层，节点数为8，那么专家网络和塔网络总的参数为$100\times 16\times 8+16\times 8\times 2=13056$，对于基线Share-Bottom，塔网络节点也设置为8，共享层节点设置为$13056/(100+8\times 2)\times 2\simeq 13$
结果：所有模型使用Adam优化器，学习率从$[0.0001,0.001,0.1]$网格搜索。结果如下
（1）所有模型在高相关性的多任务学习上都比低相关性的多任务表现要好
（2）任务间相关性的差异对模型效果的影响，MMoE比MoE和Share-Bottom显著小。极端情况下，两个任务完全相同，MMoE和MoE表现一致，但是随着任务相关性变低，MoE表现下降显著，而MMoE变化很小。
（3）所有场景MoE都比Share-Bottom要好，说明MoE的结构是有增益的。

Model Structures. The input dimension is 100. Both MoE based models have 8 experts with each expert implemented as a single- layer network. The size of the hidden layers in the expert network is 16. The tower networks are still single-layer networks with size=8. We note that the total number of model parameters in the shared experts and the towers is 100 × 16 × 8 + 16 × 8 × 2 = 13056. For the baseline Shared-Bottom model, we still set the tower network as a single-layer network with size=8. We set the single-layer shared bottom network with size 13056/(100 + 8 × 2) ≈ 113.
Results. All the models are trained with the Adam optimizer and the learning rate is grid searched from [0.0001, 0.001, 0.01]. For each model-correlation pair setting, we have 200 runs with independent random data generation and model initialization. The average results are shown in figure 4. The observations are outlined as follows:
(1) For all models, the performance on the data with higher correlation is better than that on the data with lower corre- lation.
(2) The gap between performances on data with different corre- lations of the MMoE model is much smaller than that of the OMoE model and the Shared-Bottom model. This trend is especially obvious when we compare the MMoE model with the OMoE model: in the extreme case where the two tasks are identical, there is almost no difference in performance between the MMoE model and the OMoE model; when the correlation between tasks decreases, however, there is an obvious degeneration of performance for the OMoE model while there is little influence on the MMoE model. There- fore, it’s critical to have task-specific gates to model the task differences in the low relatedness case.
(3) Both MoE models are better than the Shared-Bottom model in all scenarios in terms of average performance. This indi- cates that the MoE structure itself brings additional benefits. Following this observation, we show in the next subsection that the MoE models have better trainability than the Shared- Bottom model.

鲁棒性

对于大规模网络结构模型，模型的鲁棒性是非常受到关注的，即在不同的超参数设置、模型初始化上面是否鲁棒。

For large neural network models, we care much about their trainabil- ity, i.e., how robust the model is within a range of hyper-parameter settings and model initializations.

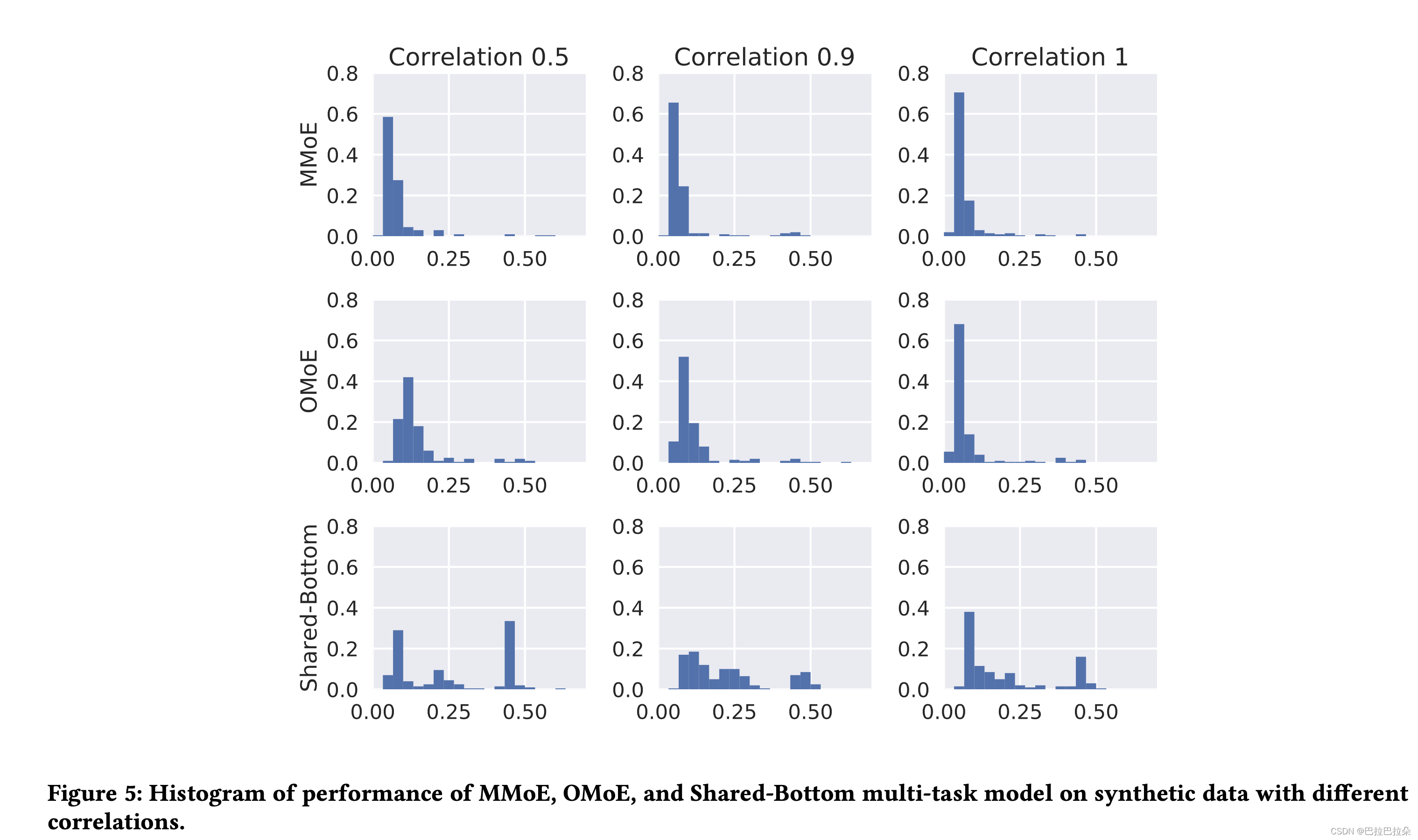
最近的一些发现一些门控RNN(像LSTM、GRU)并不是比普通的RNN效果好，而是在鲁棒性上面更强。上面已经论证了MMoE在相关性较低的多任务学习中表现较好，但同时希望新模型具有鲁棒性。因为是人工合成的数据，因此比较容易做鲁棒性的实验。每次用不同的随机种子来产生随机输入，只保证分布相同，同时模型初始化也保持不同。将loss结果绘制成Figure 5.

Recently, Collins et al [10] find that some gated RNN models (like LSTM and GRU) we thought to perform better than the vanilla RNN are simply easier to train rather than having better model capacities. While we have demonstrated that MMoE can better handle the situation where tasks are less related, we also want to have a deeper understanding how it behaves in terms of trainability.
With our synthetic data, we can naturally investigate the ro- bustness of our model against the randomness in the data and model initialization. We repeat the experiments under each setting multiple times. Each time the data are generated from the same distribution but different random seeds and the models are also initialized differently. We plot the histogram of the final loss values from repeated runs in Figure 5.

结论，首先不同的任务相关性设置下，Share-Bottom表现差异大于基于MoE结构的模型。说明Share-Bottom相比来讲更容易有低质量局部最小值。第二，当任务相关性为1时，MoE和MMoE表现相似，当相关性下降时MoE表现明显下降，说明增加的多个门控网络结构对于解决低质量局部最小值的问题上是有效果的。最后，这三个模型的最小loss是可比的，这进一步说明了显示建模任务间的关系是可取的。

实验

基线方法

L2约束： 是为具有2个任务的跨语言设计的，不同任务的参数通过L2约束软共享。给定$y_k$为任务$k$的真实值，预测表示如下，${\theta }_k$表示模型参数
${\hat{y}}_k=f(x;{\theta }_k)$
目标函数为
$$EL(y_1,f(x;{\theta }_1))+EL(y_2,f(x;{\theta }_2))+\alpha ||{\theta }_1^2-{\theta }_2^2||$$
$\alpha$是个超参数，这种方法用$\alpha$数值大小建模任务之间的相关性。

L2-Constrained [15]: This method is designed for a cross-lingual problem with two tasks. In this method, parameters used for different tasks are shared softly by an L2 constraint.

Cross-Stitch : 通过引入一个”Cross-Stitch“单元来共享两个任务之间的知识。分别以任务1和任务2的隐层$x_1$和$x_2$作为输入，输出如下
[ x ~ 1 i x ~ 2 i ] = [ a 11 a 12 a 21 a 22 ] [ x 1 i x 2 i ]

$$\begin{bmatrix} \tilde{x}_1^i\\ \tilde{x}_2^i\\ \end{bmatrix}$$ = $$\begin{bmatrix} a_{11}&a_{12}\\ a_{21}&a_{22}\\ \end{bmatrix}$$ $$\begin{bmatrix} x_1^i\\ x_2^i\\ \end{bmatrix}$$ [x~1i​x~2i​​]=[a11​a21​​a12​a22​​][x1i​x2i​​]
其中$a_{jk},j,k=1,2$表示任务$j$到任务$k$的交叉转移训练参数

Cross-Stitch [27]: This method shares knowledge between two tasks by introducing a “Cross-Stitch” unit. The Cross-Stitch unit takes the input of separated hidden layers $x_1$ and $x_2$ from task 1 and 2, and outputs ${\tilde{x}}_1^i$ and ${\tilde{x}}_2^i$ respectively by the following equation:

Tensor-Factorization: 这个方法使用张量来建模多任务权重，张量分解用来在不同任务间共享。隐层输入大小为$m$，隐层输出大小为$n$,任务书目录为$k$，权重为$W$，
$$W=\sum _{i_1}^{r1}\sum _{i_2}^{r2}\sum _{i_3}^{r3}S(i_1,i_2,i_3)\cdot U_1(:,i_1)\circ U_2(:,i_2)\circ U_3(:,i_3)$$
张量$S$大小为$m\times n\times k$，矩阵$U_1$大小$m\times r_1$，矩阵$U_2$大小$n\times r_2$，矩阵$U_3$大小$k\times r_3$，其中$r_1,r_2,r_3$是超参数。

Tensor-Factorization [34]: In this method, weights from multiple tasks are modeled as tensors and tensor factorization methods are used for parameter sharing across tasks. For our comparison, we implement Tucker decomposition for learning multi-task models, which is reported to deliver the most reliable results [34]. For ex- ample, given input hidden-layer size m, output hidden-layer size n and task number k, the weights W, which is a m × n × k tensor, is derived from the following equation:

超参数调优

使用高斯过程模型来调优。公平起见，限制每种方法的隐层最大节点数为2048。
MMoE：专家的数量，每个专家隐层的节点数
L2-Constrained：隐层数，L2约束$\alpha$
Cross-Stitch：隐层数，Cross-Stitch层数
Tensor-Factorization: 隐层数，$r_1,r_2,r_3$的大小

We adopt a hyper-parameter tuner, which is used in recent deep learning frameworks [10], to search the best hyperparameters for all the models in the experiments with real datasets. The tuning algorithm is a Gaussian Process model similar to Spearmint as introduced in [14, 32].
To make the comparison fair, we constrain the maximum model size of all methods by setting a same upper bound for the number of hidden units per layer, which is 2048. For MMoE, it is the “number of experts” × “hidden units per expert”. Our approach and all baseline methods are implemented using TensorFlow
We tune the learning rates and the number of training steps for all methods. We also tune some method-specific hyper-parameters:

人口收入普查数据

数据集描述

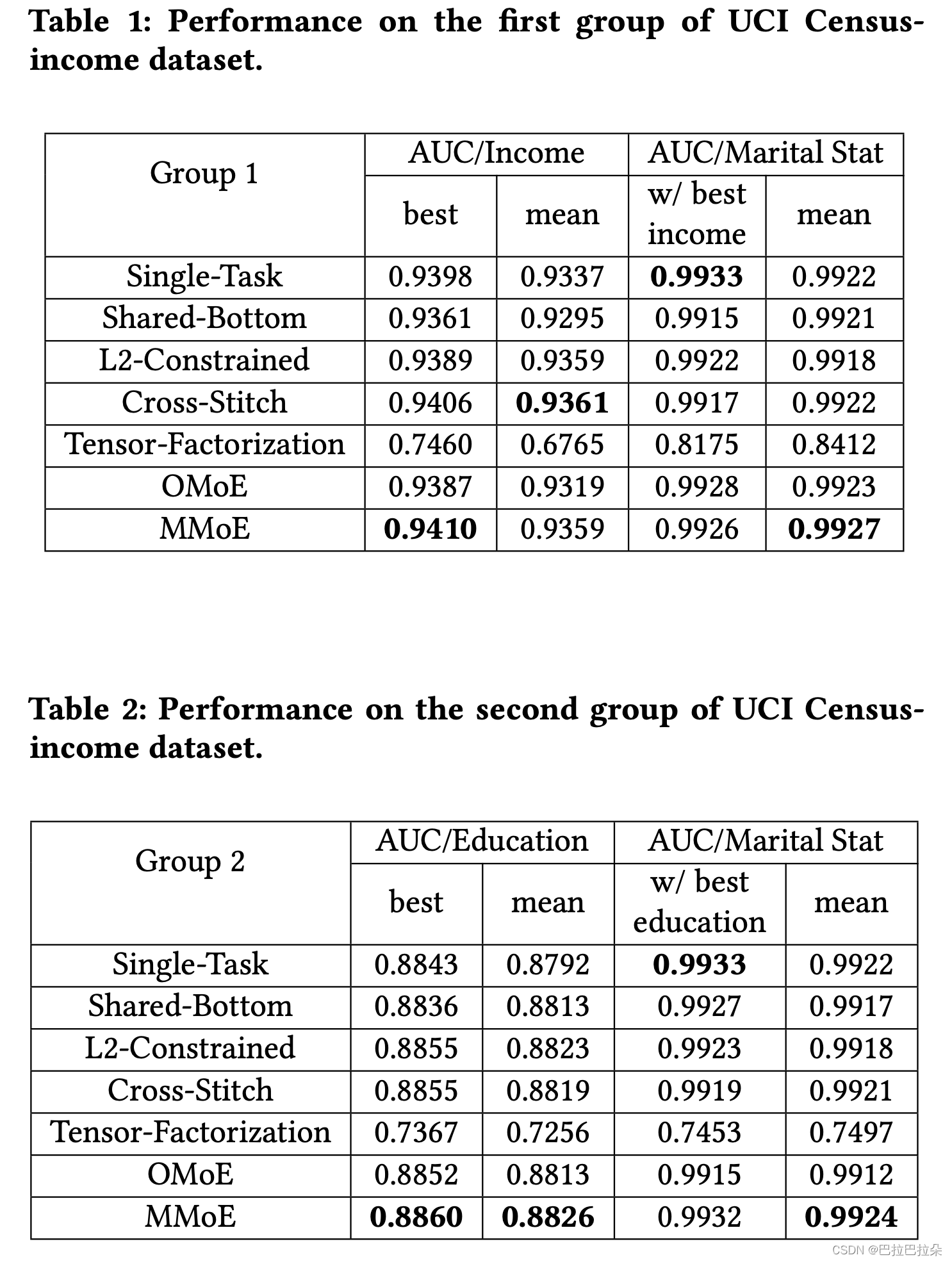
从1994年人口普查数据中抽取的收入普查数据，包含299285个样本，总共40个特征，通过设置2个特征为预测目标来构造2个多任务学习问题，通过10000个随机样本评估2个任务的皮尔逊相关系数。
（1）任务1：预测收入是否超过$50K
任务2：预测用户是否未婚
皮尔逊相关系数值为0.1768
（2）任务1：预测教育程度至少是大学
任务2：预测用户是否未婚

有1995232个训练样本和99762个测试样本，将测试样本按照1：1的比例拆分为验证集和测试集，每种方法，都会先调整超参数，找到最好的超参数再用随机的初始化参数训练400次

In the dataset, there are 199,523 training examples and 99,762 test examples. We further randomly split test examples into a validation dataset and a test dataset by the fraction of 1:1.
Note that we remove education and marital status from input features as they are treated as labels in these setups. We compare MMoE with aforementioned baseline methods. Since both groups of tasks are binary classification problems, we use AUC scores as the evaluation metrics. In both groups, we treat the marital status task as the auxiliary task, and treat the income task in the first group and the education task in the second group as the main tasks. For hyper-parameter tuning, we use the AUC of the main task on the validation set as the objective. For each method, we use the hyper-parameter tuner conducting thousands of experiments to find the best hyper-parameter setup. After the hyper-parameter tuner finds the best hyper-parameter for each method, we train each method on training dataset 400 times with random parameter initialization and report the results on the test dataset.

结果：MMoE几乎在所有的场景都是最优的

大规模内容推荐

两个任务，一个预测是否参与，一个是预测满意度

Experiment Setup. We evaluate the multi-task models by creating two binary classification tasks for the deep ranking model: (1) predicting a user engagement related behavior; (2) predicting a user satisfaction related behavior. We name these two tasks as engagement subtask and satisfaction subtask.

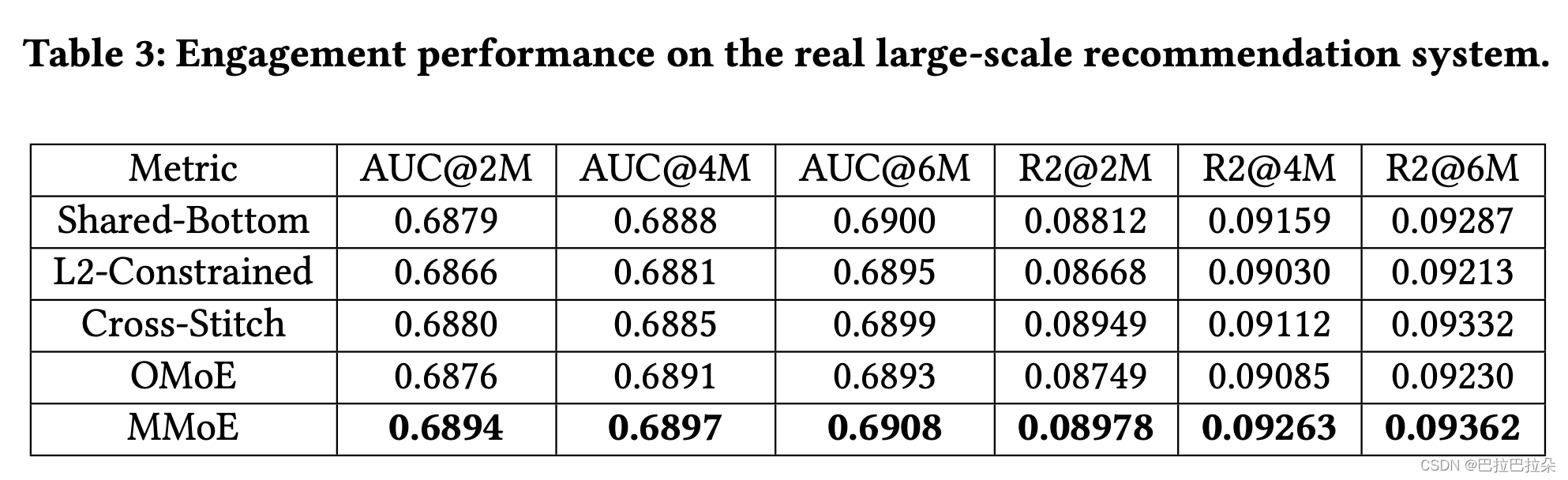
离线结果

Offline Evaluation Results. For offline evaluation, we train the models on a fixed set of 30 billion user implicit feedbacks and evaluate on a 1 million hold-out dataset. Given that the label of the satisfaction subtask is much sparser than the engagement subtask, the offline results have very high noise levels. We only show the AUC scores and R-Squared scores on the engagement subtask in Table 3.
We show the results after training 2 million steps (10 billion examples with batch size 1024), 4 million steps and 6 million steps. MMoE outperforms other models in terms of both metrics. L2- Constrained and Cross-Stitch are worse than the Shared-Bottom model. This is likely because these two models are built upon two separate single-task models and have too many model parameters to be well constrained

在线结果

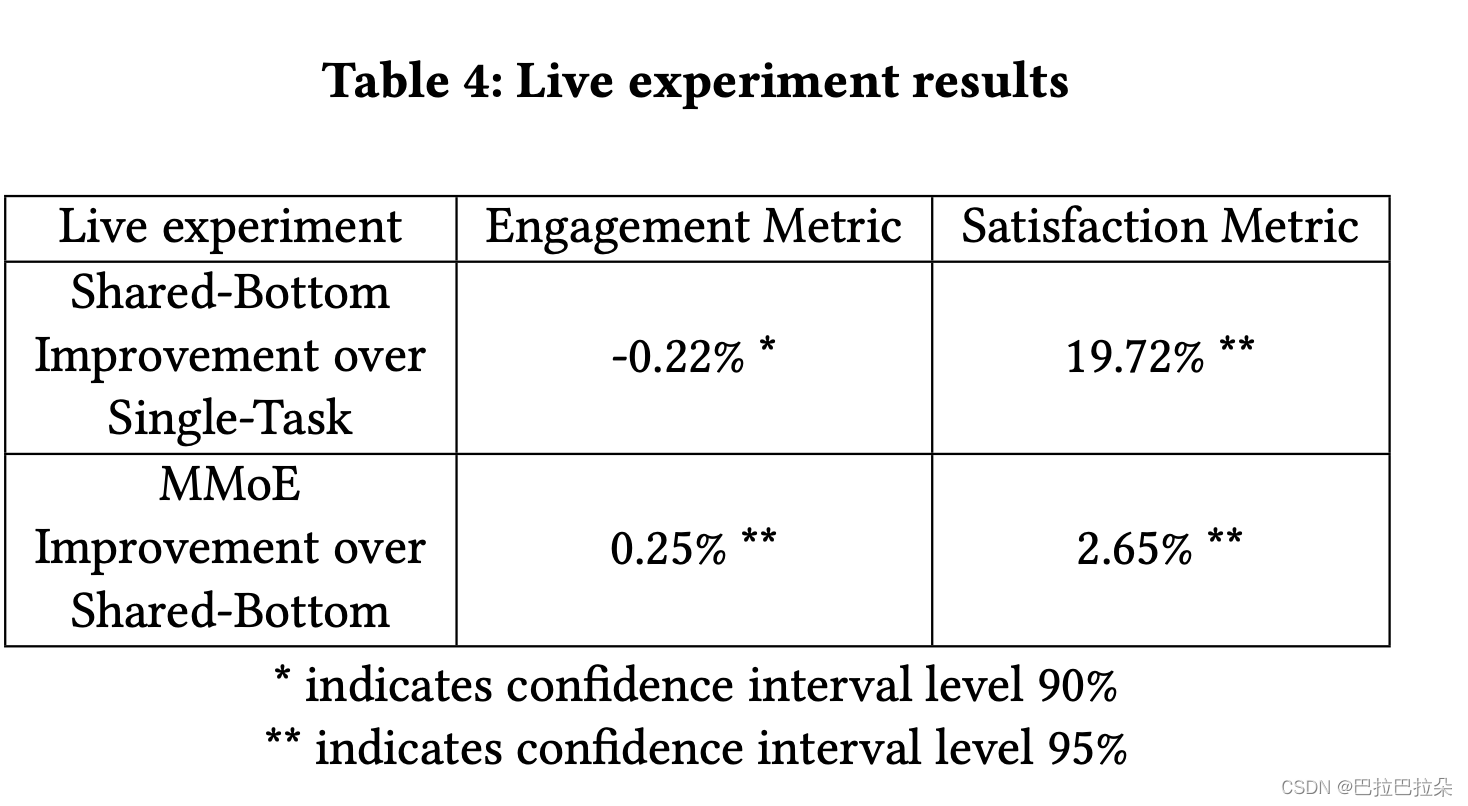
Live Experiment Results. At last, we conduct live experi- ments for our MMoE model on the content recommendation system. We do not conduct live experiments for L2-Constrained and Cross- Stitch methods because both models double the serving time by introducing more parameters.
We conduct two sets of experiments. The first experiment is to compare a Shared-Bottom model with a Single-Task model. The Shared-Bottom model is trained on both engagement subtask and satisfaction subtask. The Single-Task model is trained on the engage- ment subtask only. Note that though not trained on the satisfaction subtask, the Single-Task model serves as a ranking model at test time so we can also calculate satisfaction metrics on it. The second experiment is to compare our MMoE model with the Shared-Bottom model in the first experiment. Both experiments are done using the same amount of live traffic.
Table 4 shows the results of these live experiments. First, by using Shared-Bottom model, we see a huge improvement on the satisfaction live metric of 19.72%, and a slight decrease of -0.22% on the engagement live metric. Second, by using MMoE, we improve both metrics comparing with the Shared-Bottom model. In this recommendation system, engagement metric has a much larger raw value than the satisfaction metric, and it is desirable to have no engagement metric loss or even gains while improving satisfaction metric.