AVL树平衡二叉搜索树详解--实现插入_创建平衡二叉搜索树类并实现插入元素的算法。

• 我们之前所学习的二叉搜索树由于可能出现单边树的极端情况，导致效率为O(N)。因此，本文将介绍AVL树即平衡搜索二叉树，将可以有效的避免单边树的情况。

AVL树的概念

当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

• 它的左右子树都是AVL树
• 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

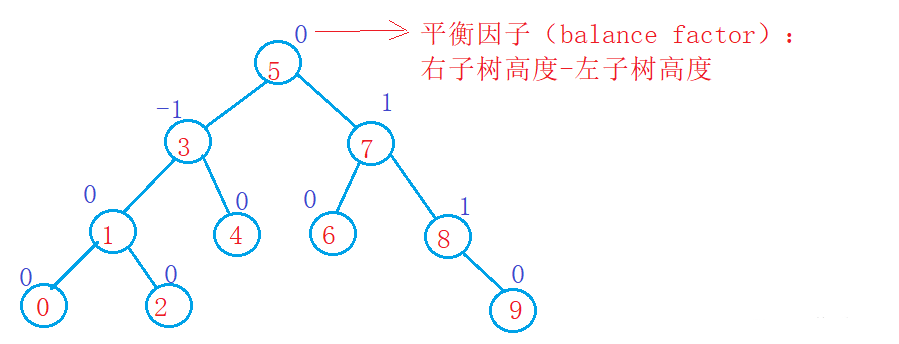
如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在O（log2N） ，搜索时间复杂度O( log2N)。

AVL树的定义

Node节点的定义

template <class K, class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	int _bf;//平衡因子，右子树高度-左子树高度

	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
	{}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

树的定义

template <class K, class V>
class AVLTree
{
    typedef AVLTreeNode<K, V> Node
private:
	Node* _root;
private:
    //旋转相关函数;
	void* RotateL(Node* parent);
	void* RotateR(Node* parent);
	void* RotateRL(Node* parent);
	void* RotateLR(Node* parent);
public:
	;
	AVLTree()
		:_root(nullptr)
	{}

	bool Insert(const pair<K, V>& kv)//插入
	{}

	bool Earse();//类似于BST树的删除，只不过需要旋转+要调整平衡因子，我们不做深究;


	//中序遍历验证
	void _Inorder(Node* root)
	{
		if (!root) return;
		_Inorder(root->_left);
		 cout << (_root->_kv).first<<" : "<<((_root->_kv)).second << endl;
		_Inorder(root->_right);
	}
	void Inorder() { _Inorder(_root) };




};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

AVL树的插入操作

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么AVL树的插入 过程可以分为两步：

1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子

平衡因子更新情况

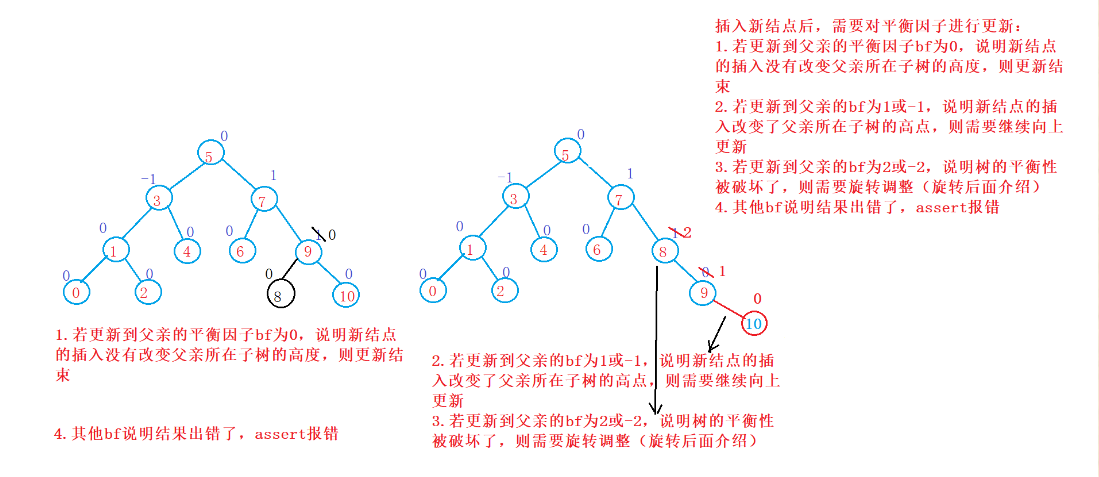
至于上面平衡因子的更新，我们需要借助“旋转”操作来更新：

AVL树的旋转(+调平衡因子)

右单旋

当结点的平衡因子出现异常时，若左子树高度高于右子树高度，那么该结点需要进行右单旋调整。
如图,进行右单旋的条件为：parent的bf为-2且subL的bf为-1。

void RotateR(Node* parent)
	{
		//改变链接关系;
		Node* SubL = parent->_left;
		Node* SubLR = SubL->_right;

		parent->_left = SubLR;
		SubL->_right = parent;
		//小心SubLR为空
		if (SubLR) SubLR->_parent = parent;

		//更新_parent指针
		Node* pparent = parent->_parent;
		parent->_parent = SubL;
		SubL->_parent = pparent;

		if (_root == parent) _root = SubL;
		else
		{
			if (pparent->_left == parent)
			{
				pparent->_left = SubL;
			}
			else
			{
				pparent->_right = SubL;
			}
		}
		//更新平衡因子;
		SubL->_bf = parent->_bf = 0;

	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

左单旋

与右单旋类似的，若左子树高度高于右子树高度，那么该结点需要进行左单旋调整。
如图,进行左单旋的条件为：parent的bf为2且subL的bf为1

	void RotateL(Node* parent)
	{
		Node* SubR = parent->_right;
		Node* SubRL = SubR->_left;

		parent->_right = SubRL;
		SubR->_left = parent;

		if (SubRL)  SubRL->_parent = parent;

		Node* pparent = parent->_parent;
		parent->_parent = SubR;
		SubR->_parent = pparent;
		if (parent == _root) _root = SubR;
		else
		{
			if (pparent->_left == parent) {
				pparent->_left = SubR;
			}
			else {
				pparent->_right = SubR;
			}
		}

		//平衡因子
		SubR->_bf = parent->_bf = 0;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

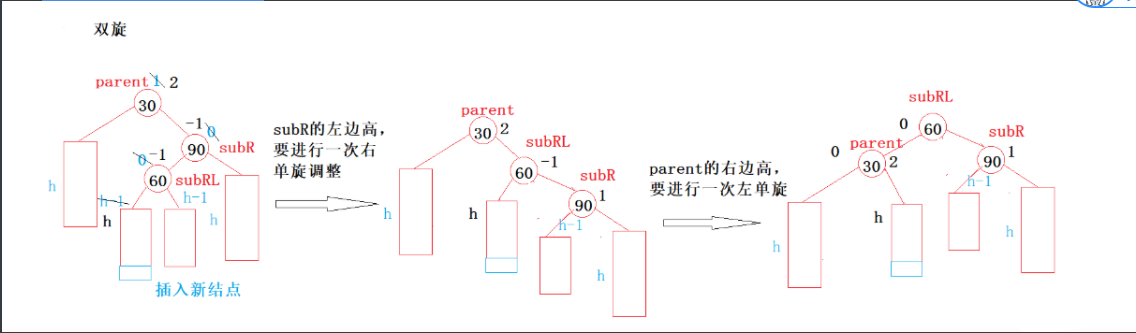
右左双旋

​ 如图,进行右左双旋的条件为：parent的bf为2且subR的bf为-1.

//别忘记每次调整完毕需要调整平衡因子！仔细画图分析;
	void RotateRL(Node* parent)
	{
		Node* SubR = parent->_right;
		Node* SubRL = SubR->_left;
		int bf = SubRL->_bf;   //以SubRL这个为依据，分类讨论后续的平衡因子情况； 

		RotateR(SubR);
		RotateL(parent);
		

		if (_bf == 0) {//SubRL就是新增节点; 
			SubR->_bf = parent->_bf = SubRL->_bf = 0;
		}
		else if (_bf == -1) {//设无关的子树高度为h，SuBRL的左右子树根据分类情况设置为一个1，一个-1，然后画图旋转判断新的bf;
			SubR->_bf = 1;
			parent = 0;
			SubRL = 0;
		}
		else if (_bf == 1) {
			SubR->_bf = 0;
			parent = -1;
			SubRL = 0;
		}
		else {//非法情况;
			assert(_bf);
		}

	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

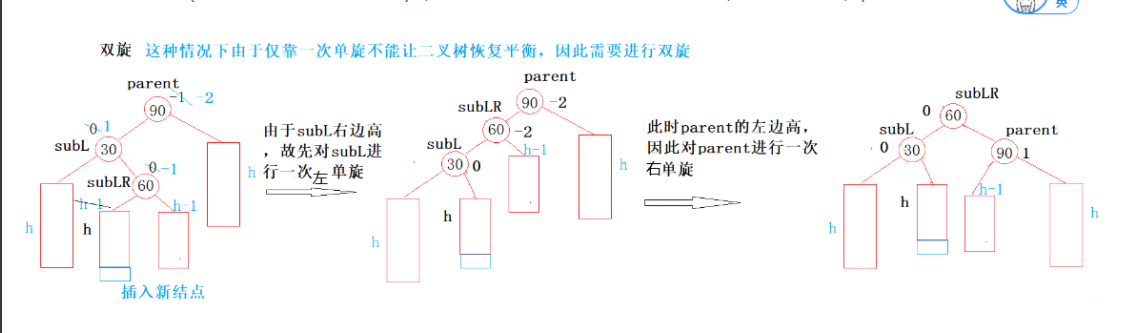
左右双旋

​ 如图,进行左右双旋的条件为：parent的bf为-2且subL的bf为1.

void RotateLR(Node* parent)
	{
		Node* SubL = parent->_left;	
		Node* SubLR = SubL ->_right;
		int bf = SubLR->_bf;

		RotateR(SubL);
		RotateL(parent);


		if (_bf == 0) {//SubRL就是新增节点;
			SubL->_bf = parent->_bf = SubLR->_bf= 0;
		}
		else if (_bf == 1) {
			SubL->_bf = -1;
			SubLR->_bf = 0;
			parent->_bf = 0;
		}
		else if (_bf == -1) {
			SubL->_bf = 0;
			SubLR->_bf = 0;
			parent->_bf = 1;
		}
		else {//非法情况;
			assert(_bf);
		}
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

AVL树整体插入代码

	bool Insert(const pair<K, V>& kv)//插入
	{	
		//类似于二叉搜索树; 先find位置，再insert
		if (_root == nullptr) {
			_root = new Node(kv);
			return true;
		}

		Node* cur = _root;
		Node* parent = cur;
		while (cur)
		{
			if ((cur->_kv).first > kv.first) {
				parent = cur;
				cur = cur->_left;
			}
			else if ((cur->_kv).first < kv.first) {
				parent = cur;
				cur = cur->_right;
			}
			else {//数据冗余 插入错误
				return false;
			}
		}
		
		cur =new Node(kv);
		cur->_bf = 0;
		cur->_parent = parent;

	
		if (parent->_kv.first >cur->_kv.first) {
			parent->_left = cur;	
			//(parent->_bf)--;		 调平衡因子放下面while里轮训来,重要作用！！不然只能调一次，parent的parent就没法变了;
		}
		else {
			parent->_right = cur;
			//(parent->_bf)++;
		}
		

		//插完了 得整体调整_bf了; 可能连续向上调整，也可能 不 调 整 插入以后父节点bf变0？
		
	
		//核心部分！
		while (parent)
		{
			if (parent->_left == cur)
				parent->_bf--;
			else
				parent->_bf++;

			//不用调整 插完父节点bf=0了; 直接break 插入完毕
			if (parent->_bf == 0) break;
			//可能需要调整，插完 父节点出现gap了，父节点虽然满足 但是得 向上继续看是否调整; 《一层一层节点向上检索需不需要旋转;》
			else if (parent->_bf == 1 || parent->_bf == -1) {
				cur = parent;
				parent = parent->_parent;
			}
			//需要调整了;
			else if (parent->_bf == 2 || parent->_bf == -2) {

				//右单旋
				if (parent->_bf == -2 && cur->_bf == -1) {//这里画图分析条件，因为parent，cur都向上迭代过一次了，所以其实parent == pparent， cur == parent，他们两个就是我们用来判断旋转方法的节点了！
					RotateR(parent);
				}
				//左单旋
				else if (parent->_bf == 2 && cur->_bf == 1) {
					RotateL(parent);
				}
				//左 右双旋
				else if (parent->_bf == -2 && cur->_bf == 1) {
					RotateLR(parent);
				}
				//右 左双旋
				else if (parent->_bf == 2 && cur->_bf == -1) {
					RotateRL(parent);
				}
				break;//调整完必满足AVL性质 break 插入完毕
			}
			else//若parent的bf为其他情况（不是 0 or +-1 or +-2），说明搜索树的平衡已经破坏，报错
				assert(false);


		}

		
		return true;

	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

验证AVL树

中序遍历即可验证BST树的性质，下面是刷题中用到的自底向上判断avl树;

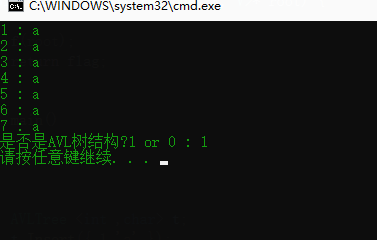
int flag = 1;//是否是AVL树的标记;
template<class K,class V>
int f(AVLTreeNode<K,V>* cur)
{
	if (!cur) return 0;
	int a = f(cur->_left) + 1;//自底向上递归
	int b = f(cur->_right) + 1;
	if (a - b > 1 || b - a > 1) flag = false;
	return max(a, b);
}
template<class K, class V>
bool isBalanced(AVLTreeNode< K, V>* root) {

	f(root);
	return flag;
}

int main()
{
    
	

	AVLTree <int ,char> t;
	t.Insert({ 1,'a' });
	t.Insert({ 2,'a' });
	t.Insert({ 3,'a' });
	t.Insert({ 3,'a' });
	t.Insert({ 4,'a' });
	t.Insert({ 5,'a' });
	t.Insert({ 6,'a' });
	t.Insert({ 7,'a' });
	
	t.Inorder();

	cout << "是否是AVL树结构?1 or 0 : " << flag << endl;
    return 0;

}
    
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

AVL树的性能分析

AVL树是一棵绝对平衡的二叉搜索树,因为每个节点的平衡因子gap不超过1;这样可以保证查询时高效的时间复杂度，即log2(N) ;

但是:如果要对AVL树做一些结构修改的操作，性能非常低下:

比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。

因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(不改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。

后续红黑树针对avl树的优化即将登场！