图像处理合集：图像基础操作（图像翻转、图像锐化、图像平滑等）、图像阈值分割（边缘检测、迭代法、OSTU、区域增长法等）、图像特征提取（图像分割、灰度共生矩阵、PCA图像压缩）_图像处理技术

说明

本文记录数字图像处理相关问题。导入的依赖如下：

import cv2
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
matplotlib.rcParams['font.sans-serif'] = ['SimHei']     # 显示中文
# 为了坐标轴负号正常显示。matplotlib默认不支持中文，设置中文字体后，负号会显示异常。需要手动将坐标轴负号设为False才能正常显示负号。
matplotlib.rcParams['axes.unicode_minus'] = False
1
2
3
4
5
6
7
8

一、图像锐化或增强相关

1. 图像点处理

1.1 图像翻转

img = Image.open("data//Lenna.jpg")
plt.subplot(2, 2, 1)
plt.imshow(img)
plt.title("原图")
img_lR = img.transpose(Image.FLIP_LEFT_RIGHT)  #上下翻转则调成TOP_BUTTOM 
plt.subplot(2, 2, 2)
plt.imshow(img_lR)
plt.title("左右翻转")
plt.show()
1
2
3
4
5
6
7
8
9

结果如下：

1.2 幂运算和对数运算

img = cv2.imread("data//cameraman.tif")
plt.subplot(2, 2, 1)
plt.imshow(img)
plt.title("原图")
img_pow = cv2.pow(src=img, power=2)
plt.subplot(2, 2, 2)
plt.imshow(img_pow)
plt.title("2次幂")
img = np.float32(img)
img_log = cv2.log(img)
plt.subplot(2, 2, 3)
plt.imshow(img_log)
plt.title("对数")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14

结果如下：

2. 直方图处理

分析：直方图简单来说就是图像中每个像素值的个数统计。直方图均衡化就是用来改善图像的全局亮度和对比度。
均衡化作用：将原来比较少像素的灰度分配到别的灰度中，像素相对集中，均衡后灰度范围变大，对比度变大，清晰度变大，故能有效地增强图像。

# 均衡化
def hist_equal(img, z_max=255):
    H, W = img.shape
    S = H * W * 1.
    out = img.copy()
    sum_h = 0.
    for i in range(1, 255):
        ind = np.where(img == i)
        sum_h += len(img[ind])
        z_prime = z_max / S * sum_h
        out[ind] = z_prime
    out = out.astype(np.uint8)
    return out

 
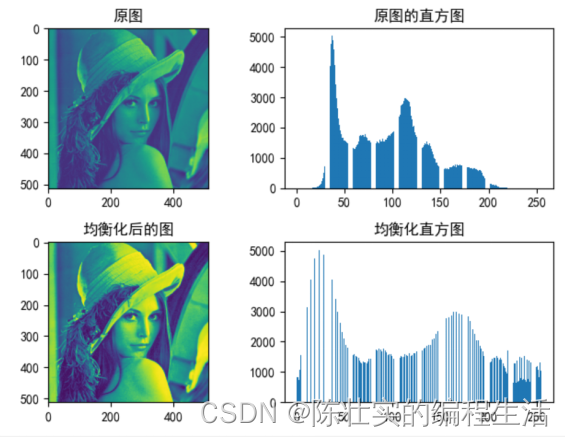
# 3.直方图处理
img = cv2.imread("data//Lenna.jpg", 0).astype(np.float32)
plt.subplot(2, 2, 1)
plt.imshow(img)
plt.title("原图")

plt.subplot(2, 2, 2)
plt.hist(img.ravel(), bins=255, rwidth=0.8, range=(0, 255))
plt.title("原图的直方图")

img_hist = hist_equal(img)
plt.subplot(2, 2, 3)
plt.imshow(img_hist)
plt.title("均衡化后的图")

plt.subplot(2, 2, 4)
plt.hist(img_hist.ravel(), bins=255, rwidth=0.8, range=(0, 255))
plt.title("均衡化直方图")

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

结果：

3. 图像平滑

图像平滑是一种区域增强算法，平滑算法有：均值滤波、中值滤波、高斯滤波等。
均值滤波：指任意一点的像素值，都是周围N*M个像素值的均值。
中值滤波：中值滤波是非线性的图像处理方法，在去噪的同时可以兼顾到边界信息的保留。具体做法：选一个含有奇数点的窗口W，将这个窗口在图像上扫描，把窗口中所含的像素点按灰度级的升或降序排列，取位于中间的灰度值来代替该点的灰度值。
高斯滤波：图像高斯平滑也是邻域平均的思想对图像进行平滑的一种方法，在图像高斯平滑中，对图像进行平均时，不同位置的像素被赋予了不同的权重。
方框滤波：和均值滤波差不多，区别在于需不需要均一化处理。

# 4. 图像平滑： 用不同大小的核进行均值滤波、中值滤波、高斯滤波等。
# 4.0 读取原图
img = cv2.imread("data//Lenna.jpg")
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)  # 调整通道顺序，解决imread图片读取发蓝的问题
plt.subplot(3, 2, 1)
plt.imshow(img)
plt.title("原图")
# 4.1 均值滤波
img_avg = cv2.blur(src=img, ksize=(5, 5))
plt.subplot(3, 2, 2)
plt.imshow(img_avg)
plt.title("均值滤波")
# 4.2 中值滤波
img_median = cv2.medianBlur(src=img, ksize=5)
plt.subplot(3, 2, 3)
plt.imshow(img_median)
plt.title("中值滤波")
# 4.3 高斯滤波
img_gauss = cv2.GaussianBlur(img, ksize=(5, 5),sigmaX=0)
plt.subplot(3, 2, 4)
plt.imshow(img_median)
plt.title("高斯滤波")
# 4.4 方框滤波
img_fang = cv2.boxFilter(src=img, ddepth=-1, ksize=(5, 5), normalize=1)  # normalize=1表示做归一化处理
plt.subplot(3, 2, 5)
plt.imshow(img_median)
plt.title("方框滤波")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

结果：

4. 图像锐化

Laplacian算子是图像的二阶导，可以检测图像灰度的快速变化，经常用于图像的边缘检测。正常图像中边界清晰，经拉普拉斯计算后方差较大；模糊图像边界信息少，方差小。所以，可以利用拉普拉斯算子做图像的模糊检测。

# 5.图像锐化： 计算laplacian图像、梯度图像。
img = cv2.imread("data//Lenna.jpg")
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)  # 调整通道顺序，解决imread图片读取发蓝的问题
plt.subplot(3, 2, 1)
plt.imshow(img)
plt.title("原图")

# 5.1 Laplacian
img_Laplacian = cv2.Laplacian(src=img, ddepth=-1, ksize=3)  # ddept=-1表示和原图像一样的深度，可调节
plt.subplot(3, 2, 2)
plt.imshow(img_Laplacian)
plt.title("Laplacian")

# 5.2 Sobel
img_sobel = cv2.Sobel(src=img, ddepth=cv2.CV_64F, dx=1, dy=0, ksize=3)
plt.subplot(3, 2, 3)
plt.imshow(img_sobel)
plt.title("sobel")

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

结果：

5. 图像增强

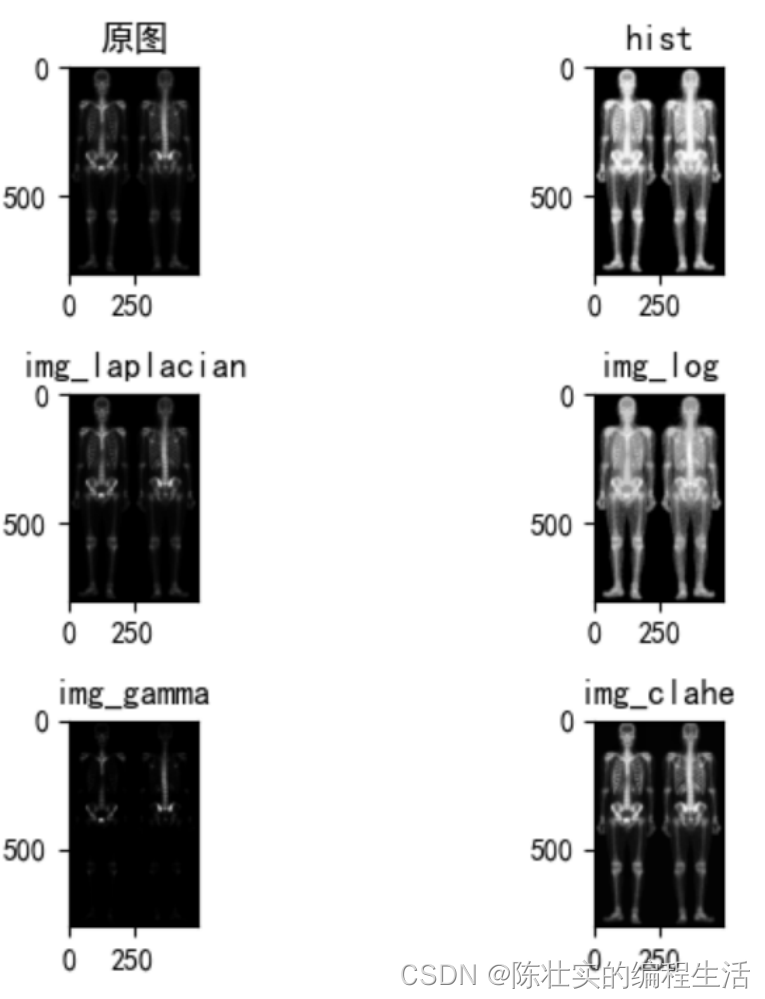
图像增强有很多方式，本文采用了直方图均衡、拉普拉斯算子、对数变换、伽马变换、限制对比度自适应直方图均衡化来进行图像增强。

# 直方图均衡增强
def hist(image):
    r, g, b = cv2.split(image)
    r1 = cv2.equalizeHist(r)
    g1 = cv2.equalizeHist(g)
    b1 = cv2.equalizeHist(b)
    image_equal_clo = cv2.merge([r1, g1, b1])
    return image_equal_clo

# 拉普拉斯算子
def laplacian(image):
    kernel = np.array([[0, -1, 0], [-1, 5, -1], [0, -1, 0]])
    image_lap = cv2.filter2D(image, cv2.CV_8UC3, kernel)
    return image_lap

# 对数变换
def log(image):
    image_log = np.uint8(np.log(np.array(image) + 1))
    cv2.normalize(image_log, image_log, 0, 255, cv2.NORM_MINMAX)
    # 转换成8bit图像显示
    cv2.convertScaleAbs(image_log, image_log)
    return image_log

# 伽马变换
def gamma(image):
    fgamma = 2
    image_gamma = np.uint8(np.power((np.array(image) / 255.0), fgamma) * 255.0)
    cv2.normalize(image_gamma, image_gamma, 0, 255, cv2.NORM_MINMAX)
    cv2.convertScaleAbs(image_gamma, image_gamma)
    return image_gamma

# 限制对比度自适应直方图均衡化CLAHE
def clahe(image):
    b, g, r = cv2.split(image)
    clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8))
    b = clahe.apply(b)
    g = clahe.apply(g)
    r = clahe.apply(r)
    image_clahe = cv2.merge([b, g, r])
    return image_clahe

img = cv2.imread("data//fig3_43.tif")
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)  # 调整通道顺序，解决imread图片读取发蓝的问题
plt.subplot(3, 2, 1)
plt.imshow(img)
plt.title("原图")

# 6.1 使用直方图增强
img_hist = hist(img)
plt.subplot(3, 2, 2)
plt.imshow(img_hist)
plt.title("hist")

# 6.2 使用拉普拉斯算子增强
img_laplacian = laplacian(img)
plt.subplot(3, 2, 3)
plt.imshow(img_laplacian)
plt.title("img_laplacian")

# 6.3使用对数变换增强
img_log = log(img)
plt.subplot(3, 2, 4)
plt.imshow(img_log)
plt.title("img_log")

# 6.4 使用伽马变换增强
img_gamma = gamma(img)
plt.subplot(3, 2, 5)
plt.imshow(img_gamma)
plt.title("img_gamma")

# 6.5 限制对比度自适应直方图均衡化CLAHE
img_clahe = clahe(img)
plt.subplot(3, 2, 6)
plt.imshow(img_clahe)
plt.title("img_clahe")

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

结果如下：

二、图像阈值分割

1. 边缘检测

（1）分别使用sobel、prewits、LoG和canny算子检测图像边缘；

​ 其代码如下：

# 读取图像
img = cv2.imread('data//fig10_16a.tif')
img_RGB = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)  # 转成RGB 方便后面显示
# 灰度化处理图像
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 高斯滤波
gaussianBlur = cv2.GaussianBlur(grayImage, (3, 3), 0)
# 阈值处理
ret, binary = cv2.threshold(gaussianBlur, 127, 255, cv2.THRESH_BINARY)
# Prewitt算子
kernelx = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]], dtype=int)
kernely = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]], dtype=int)
x = cv2.filter2D(binary, cv2.CV_16S, kernelx)
y = cv2.filter2D(binary, cv2.CV_16S, kernely)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Prewitt = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
# Sobel算子
x = cv2.Sobel(binary, cv2.CV_16S, 1, 0)
y = cv2.Sobel(binary, cv2.CV_16S, 0, 1)

absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Sobel = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)

# log
def log(image):
    image_log = np.uint8(np.log(np.array(image) + 1))
    cv2.normalize(image_log, image_log, 0, 255, cv2.NORM_MINMAX)
    # 转换成8bit图像显示
    cv2.convertScaleAbs(image_log, image_log)
    return image_log
img_log = log(img_RGB)
# canny算子
img_canny = cv2.Canny(image=gaussianBlur, threshold1=50, threshold2=150)
#显示图形
plt.subplot(231), plt.imshow(img_RGB), plt.title('原始图像'), plt.axis('off')  # 坐标轴关闭
plt.subplot(232), plt.imshow(Sobel, cmap=plt.cm.gray), plt.title('Sobel算子'), plt.axis('off')
plt.subplot(233), plt.imshow(Prewitt, cmap=plt.cm.gray), plt.title('Prewitt算子'), plt.axis('off')
plt.subplot(234), plt.imshow(img_log, cmap=plt.cm.gray), plt.title('log算子'), plt.axis('off')
plt.subplot(235), plt.imshow(img_canny, cmap=plt.cm.gray), plt.title('Canny算子'), plt.axis('off')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

显示效果：

2. 阈值分割

2.1 迭代法

分析：迭代法是通过最小概率误判来实现的。通过最小概率误判推导出阈值 $T$
$$T=\frac{1}{2}(m_1+m_2)$$

之后进行迭代进行分割，迭代步骤如下:

​ Step1: 为全局阈值 $T$ 选择一个初始值；

​ Step2: 用 $T$ 对图像进行分割。将产生两组像素，$G_1$ 由灰度值大于 $T$ 的所有像素组成，$ G_1 $ 由像素小于等于 $T$ 的像素组成；

​ Step3: 对 $ G_1$ 和 $G_2$ 像素分别计算平均灰度值 $m_1$ 和 $m_2$ ；

​ Step4: 更新阈值 $T$：
$$T=\frac{1}{2}(m_1+m_2)$$
​ Step5: 重复步骤2到步骤4，直到迭代到前后 $T$ 值间的差小于一个预设参数为止。

​ 代码:

# 2.1 对图10.39（a）图像，分别用迭代法和Otsu法进行分割；
# 迭代法求阈值分割
def ThresholdSegmentationByIteration(imgDesk, delta):
    """
    :param imgDesk: 需要进行阈值分割的灰度图像
    :param delta: 预设的可接受的前后阈值的差值
    :return:
    """
    T = imgDesk.mean()  # 求平均灰度值
    while True:
        T0 = imgDesk[imgDesk < T].mean()
        T1 = imgDesk[imgDesk >= T].mean()
        T_new = (T0+T1)/2
        if abs(T_new - T) < delta:
            break
        else:
            T = T_new
    best_T = int(T)     # 取整
    _, img_new = cv2.threshold(imgDesk, best_T, 255, cv2.THRESH_BINARY)
    return img_new, best_T


img_desk = cv2.imread('data//fig10_39a.tif', 0)
img_desk = cv2.cvtColor(img_desk, cv2.COLOR_BGR2RGB)  # 调整通道顺序，解决imread图片读取发蓝的问题
imgShow(img_desk, 1, 2, 1, "原图", False)
img_new, bestT = ThresholdSegmentationByIteration(imgDesk=img_desk, delta=0.1)
imgShow(img_new, 1, 2, 2, "迭代法, bestT=" + str(bestT), True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

​ 结果：

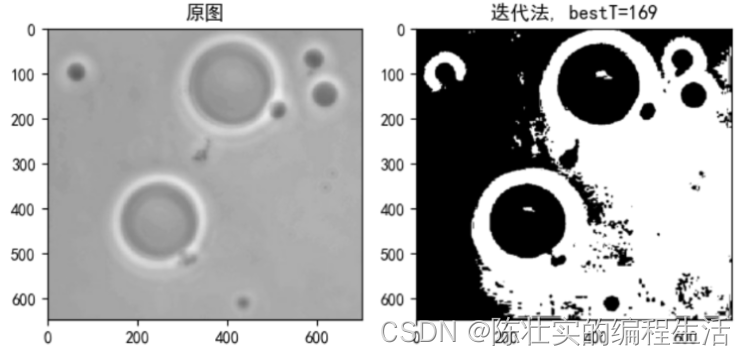
图片效果需要花时间去调节，没怎么去调参。

2.2 OSTU法

​ 分析： Ostu法又称最大类间方差法。其基本思想是用一个阈值将图像中的像素分为两类，一类小于阈值，一类大于或等于阈值。如果两个类中像素点的方差越大，则说明获得的阈值是最佳阈值。求解方法一般通过遍历的办法来更新阈值。

​ 代码：

# Otsu求解
def ThresholdSegmentationByOTSU(imgDesk):
    bestT, img_new = cv2.threshold(imgDesk, 0, 255, cv2.THRESH_OTSU)
    return bestT, img_new


img_desk = cv2.imread('data//fig10_39a.tif')
img_desk = cv2.cvtColor(img_desk, cv2.COLOR_BGR2RGB)    # 调整通道顺序，解决imread图片读取发蓝的问题
imgShow(img_desk, 1, 2, 1, "原图", False)
img_desk = cv2.cvtColor(img_desk, cv2.COLOR_BGR2GRAY)   # 提取灰度图像 
bestT, img_new = ThresholdSegmentationByOTSU(imgDesk=img_desk)
imgShow(img_new, 1, 2, 2, "OSTU, bestT=" + str(bestT), True)
1
2
3
4
5
6
7
8
9
10
11
12

​ 结果：
这个效果感觉要比迭代法要好一些。

2.3 利用边缘改进阈值进行分割

​ 分析： 利用边缘的阈值分割算法有很多，多次测试，本文选择用log算子进行改进，改进后再使用OSTU算法进行分割。
​ 代码：

# 对数变换
def log(image):
    image_log = np.uint8(np.log(np.array(image) + 1))
    cv2.normalize(image_log, image_log, 0, 255, cv2.NORM_MINMAX)
    # 转换成8bit图像显示
    cv2.convertScaleAbs(image_log, image_log)
    return image_log

img_desk = cv2.imread('data//fig10_39a.tif')
img_desk = cv2.cvtColor(img_desk, cv2.COLOR_BGR2RGB)    # 调整通道顺序，解决imread图片读取发蓝的问题
imgShow(img_desk, 2, 2, 1, "原图", False)
img_desk = log(img_desk)
img_desk = cv2.cvtColor(img_desk, cv2.COLOR_BGR2GRAY)   # 提取灰度图像
bestT, img_new = ThresholdSegmentationByOTSU(imgDesk=img_desk)
img_new = cv2.cvtColor(img_new, 0)
imgShow(img_new, 2, 2, 2, "OSTU, bestT=" + str(bestT), True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

​ 结果：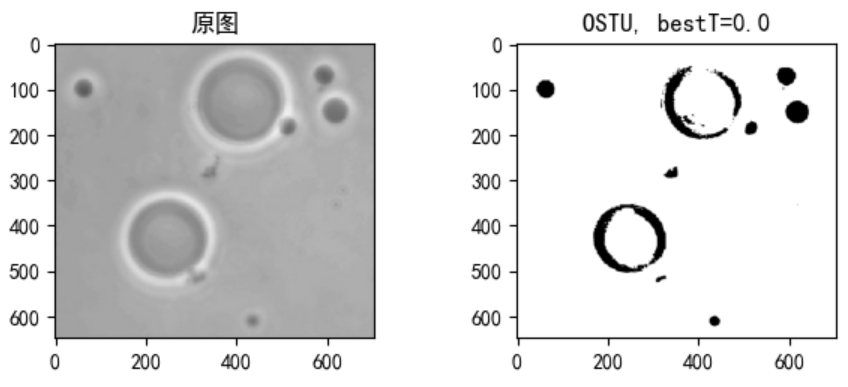

2.4 基于局部图像特征的可变阈值分割

分析： 当背景照明非常不均匀时，全局阈值处理就效果通常会很差。在这种情况下，可以使用可变阈值进行处理。其做法是利用局部区域像素点的平均值或高斯加权均值作为阈值，来进行阈值分割。
​ 代码：

#（3）对图10.48（a）图像，进行基于局部图像特征的可变阈值分割；
img_desk = cv2.imread('data//fig10_48a.tif')
img_desk = cv2.cvtColor(img_desk, cv2.COLOR_BGR2RGB)    # 调整通道顺序，解决imread图片读取发蓝的问题
imgShow(img_desk, 2, 2, 1, "原图", False, False)
print("shape = ", img_desk.shape)
img_desk = cv2.cvtColor(img_desk, cv2.COLOR_BGR2GRAY)
print("shape = ", img_desk.shape)
img_desk = cv2.adaptiveThreshold(img_desk, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY_INV, 7, 1)
print("shape = ", img_desk.shape)
imgShow(img_desk, 2, 2, 2, "局部阈值", True, True)
1
2
3
4
5
6
7
8
9
10

​ 结果：
在有限的时间内，分割的效果感觉不是很理想，以后再进行优化。

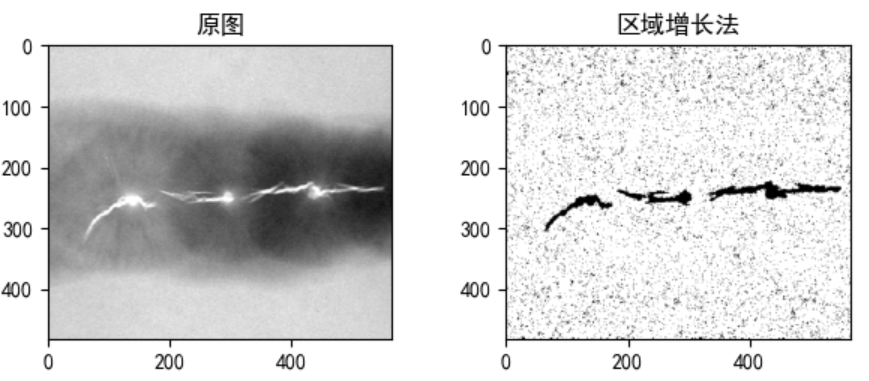
2.5 基于区域增长的分割

分析： 区域增长法考虑到区域内部和区域之间的同异性，尽量保持区域中像素的临近性和一致性的统一，更利于分辨图像真正的边界。区域增长法是在图像上选定一个种子点，记录该点的灰度值，作为一致性判断的标准阈值，此外还需要定义一个标准差。算法的主要过程如下：

​ Step1: 选取一个未被加入区域的中心点，以及设置一个阈值。

​ Step2: 依次用中心点上下左右的每一个像素的灰度值和标准阈值相减，判断结果是否小于标准差，是则将该点和种子点合并，不是则不将该点加入区域;

​ *Step2：*在区域内遍历下一个中心点，返回 Step2 ;

​ Step3: 如果本区域的点遍历完，则返回 Step1 ，直到图片内的全部点都被遍历。
​ 代码：

# ---------------------------
# @Time     : 2022/5/8 16:15
# @Author   : lcq
# @File     : test2.py
# @Function : 
# ---------------------------

import numpy as np
import cv2
import matplotlib
import matplotlib.pyplot as plt
from PIL import Image
matplotlib.rcParams['font.sans-serif'] = ['SimHei']     # 显示中文
# 为了坐标轴负号正常显示。matplotlib默认不支持中文，设置中文字体后，负号会显示异常。需要手动将坐标轴负号设为False才能正常显示负号。
matplotlib.rcParams['axes.unicode_minus'] = False


def imgShow(img, X, Y, location, title, isGray=False, isShow=False):
    plt.subplot(X, Y, location)
    if isGray:
        plt.imshow(img, cmap='gray')
    else:
        plt.imshow(img)
    plt.title(title)
    if isShow:
        plt.show()


class Point(object):
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def getX(self):
        return self.x

    def getY(self):
        return self.y


def getGrayDiff(img, currentPoint, tmpPoint):
    return abs(int(img[currentPoint.x, currentPoint.y]) - int(img[tmpPoint.x, tmpPoint.y]))


def selectConnects(p):
    if p != 0:
        connects = [Point(-1, -1), Point(0, -1), Point(1, -1), Point(1, 0), Point(1, 1), \
                    Point(0, 1), Point(-1, 1), Point(-1, 0)]
    else:
        connects = [Point(0, -1), Point(1, 0), Point(0, 1), Point(-1, 0)]
    return connects


def regionGrow(img, seeds, thresh, p=1):
    height, weight = img.shape
    seedMark = np.zeros(img.shape)
    seedList = []
    for seed in seeds:
        seedList.append(seed)
    label = 1
    connects = selectConnects(p)
    while (len(seedList) > 0):
        currentPoint = seedList.pop(0)

        seedMark[currentPoint.x, currentPoint.y] = label
        for i in range(8):
            tmpX = currentPoint.x + connects[i].x
            tmpY = currentPoint.y + connects[i].y
            if tmpX < 0 or tmpY < 0 or tmpX >= height or tmpY >= weight:
                continue
            grayDiff = getGrayDiff(img, currentPoint, Point(tmpX, tmpY))
            if grayDiff < thresh and seedMark[tmpX, tmpY] == 0:
                seedMark[tmpX, tmpY] = label
                seedList.append(Point(tmpX, tmpY))
    return seedMark


img = cv2.imread('data//fig10_51a.tif', 0)
seeds = [Point(10, 10), Point(82, 150), Point(20, 300)]
img_rg = regionGrow(img, seeds, 9)
imgShow(img, 2, 2, 1, "原图", isGray=True, isShow=False)
imgShow(img_rg, 2, 2, 2, "区域增长法", isGray=True, isShow=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

​ 结果：

三、特征提取

1. 对图像进行分割，提取下列特征

1.1 提取目标边界

分析： 轮廓检测可以利用opencv2的findContours()函数进行检测。由于该函数只接受二值化的图片，所以需要先将原图转换成二值图，再进行轮廓检测。
​代码：

# 3.1 轮廓检测
def contour_detection(img):
    # 输入的img为原图
    img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)                                            # 1.转换成灰度图
    ret, img_bin = cv2.threshold(img_gray, 127, 255, cv2.THRESH_BINARY)                         # 2.二值化
    # 3.返回contours：是一个list,list中的每一个item表示一个轮廓点的集合，如果图中有3个目标，则list中会有3个item
    # hierarchy: 是一个数组，元素个数和轮廓个数相同，每个轮廓contours[i]对应4个hierarchy元素hierarchy[i][0] ~hierarchy[i][3]，分别表示后一个轮廓、前一个轮廓、父轮廓、内嵌轮廓的索引编号，如果没有对应项，则该值为负数。
    contours, hierarchy = cv2.findContours(image=img_bin,                       # 寻找轮廓的图像
                                           mode=cv2.RETR_TREE,                  # 表示轮廓的检索模式，TREE表示建立一个等级树结构的轮廓
                                           method=cv2.CHAIN_APPROX_NONE)        # 描述轮廓的近似办法，APPROX_NONE表示存储轮廓的所有轮廓点
    cv2.drawContours(image=img_bin,         # 指明在哪幅图像上绘制轮廓
                     contours=contours,     # 需要绘制的轮廓
                     contourIdx=-1,         # 绘制哪条轮廓，如果是-1，表示绘制所有轮廓
                     color=(0, 0, 255),     # 绘制的颜色
                     thickness=3)           # 轮廓线的宽度
    return img_bin


img = cv2.imread('data//work3.jpeg')
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)          # 调整通道顺序，解决imread图片读取发蓝的问题
imgShow(img, 2, 2, 1, "原图", isGray=False, isShow=False)
img_Contour = contour_detection(img)
imgShow(img_Contour, 2, 2, 2, "轮廓图", isGray=True, isShow=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

​ 结果：

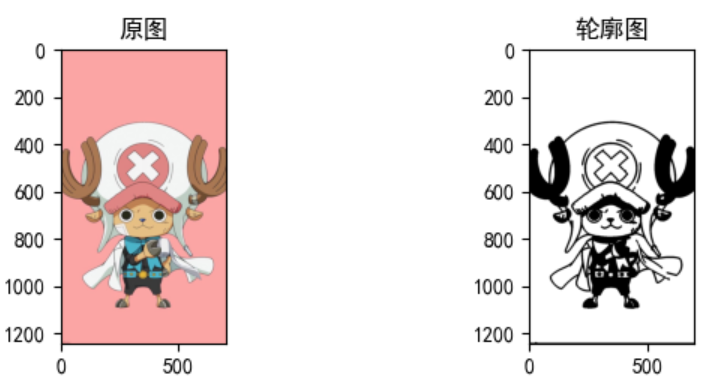由图可知，图像的轮廓绘制效果非常不错

1.2 计算目标的质心、长轴、短轴等参数

分析： 可以通过 cv2.moments(contours) 计算轮廓的距，然后轮廓的各种参数，如：
$$轮廓面积=M{[}^{\prime }m00^{\prime }]$$

$$质心:C_x=\frac{M{[}^{\prime }10^{\prime }]}{M{[}^{\prime }m00^{\prime }]},\frac{M{[}^{\prime }m01^{\prime }]}{M{[}^{\prime }00^{\prime }]}$$

通过cv2.fitEllipse()拟合椭圆来进行长轴短轴的计算.

​ 因图片复杂，轮廓较多，故随便选择轮廓1计算。

​ 代码：

# 3.1.2 计算目标的质心、长轴、短轴等参数；
index = 1
M = cv2.moments(contours[index])
cx, cy = M['m10'] / M['m00'], M['m01'] / M['m00']
print("质心"+str(index)+"坐标：", (cx, cy))
ellipse = cv2.fitEllipse(contours[1])   # ellipse包含元素:中心坐标（x, y）, 长短轴(a, b)， 角度angle: 中心旋转的角度
print("中心坐标：", ellipse[0])
print("长短轴：", ellipse[1])
print("偏转角度：", ellipse[2])
1
2
3
4
5
6
7
8
9

​ 结果：

质心1坐标： (407.66666666666663, 1084.6666666666665)
中心坐标： (406.3057861328125, 1081.3865966796875)
长短轴： (3.037715435028076, 9.131307601928711)
偏转角度： 174.8804931640625
1
2
3
4

1.3 计算边界线段的n阶统计矩；

​ 分析： 统计矩常用的有：原点矩、中心距。其计算公式如下：
$$n阶原点矩=E(X^n)$$

$$n阶中心距=E((X-EX{)}^n)$$

​ **代码： ** 因为上面图的轮廓线太多，选取编号为1的轮廓进行计算，且以2阶矩为例，具体代码如下：

# 3.1.3 计算边界线段的n阶统计矩
n = 2
E_local_n = np.mean(contours[1]**n)                             # n阶原点矩
E_center_n = np.mean((contours[1]-np.mean(contours[1]))**n)     # n阶中心矩
print("E_local_n = ", E_local_n)
print("E_center_n = ", E_center_n)
1
2
3
4
5
6

​ 结果：

E_local_n =  667805.24
E_center_n =  114328.75839999999
1
2

2、计算目标的区域描绘子。

2.1 简单描绘子，如周长、面积、均值、最大最小值等；

​ 代码：

# 3.2.1 简单描绘子，如周长、面积、均值、最大最小值等；
# 计算轮廓总周长
length = cv2.arcLength(contours[index], False)  # 计算轮廓内面积
area = cv2.contourArea(contours[index])         # 面积
avg = np.mean(contours[index])                  # 均值
max = np.max(contours[index])                   # 最大值
min = np.min(contours[index])                   # 最小值
print("轮廓1周长： ", int(length))
print("轮廓1面积： ", area)
print("轮廓1均值： ", avg)
print("轮廓1最大值： ", max)
print("轮廓1最小值： ", min)
1
2
3
4
5
6
7
8
9
10
11
12

**结果：**
1

轮廓1周长：  26
轮廓1面积：  0.5
轮廓1均值：  743.96
轮廓1最大值：  1085
轮廓1最小值：  405
1
2
3
4
5

2.2 基于灰度直方图的统计矩的描绘子；

​ 分析： 可以通过cv2.calcHist()函数获取图片的直方图数据，然后通过直方图数据进行计算各种测绘子，例如：均值、每个像素个数的最大值和最小值。

​ 代码：

# 3.2.2 基于灰度直方图的统计矩的描绘子
img = cv2.imread("data//Lenna.jpg", 0)
hist_data = cv2.calcHist(images=[img],      # 需要计算的图片数组
                    channels=[0],           # 计算哪个通道的直方图
                    mask=None,              # 掩膜，是一个大小和image一样的np数组，其中把需要处理的部分指定为1，不需要处理的部分指定为0，一般设置为None，表示处理整幅图像
                    histSize=[256],         # 使用多少个bin(柱子)，一般都是256
                    ranges=[0.0, 255.0])    # 像素范围，一般为[0, 255]
imgShow(img, 2, 2, 1, "原图", isGray=True, isShow=False)
plt.subplot(2, 2, 2)
plt.title("直方图")
plt.plot(hist_data)
plt.show()

# 计算平均像素
pixel_sum = 0
count = 0
for i in range(len(hist_data)):
    pixel_sum += i * hist_data[i]
    count += hist_data[i]
pixel_avg = pixel_sum / count
print("像素平均值： ", pixel_avg)
print("像素个数的最大值： ", np.max(hist_data))
print("像素个数的最小值： ", np.min(hist_data))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

​ 结果：

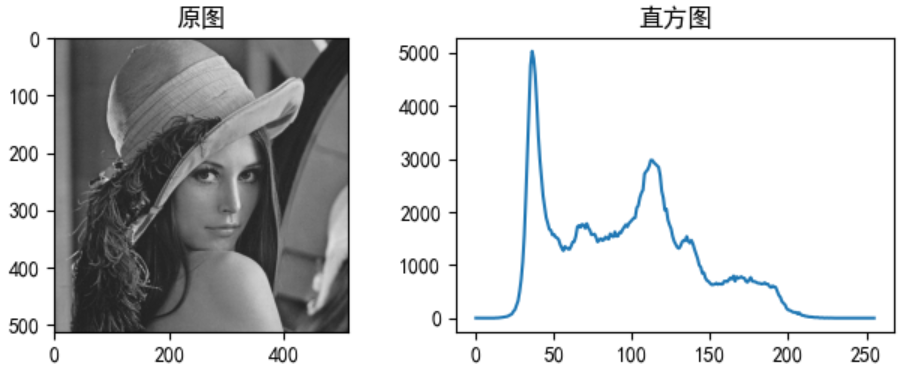
像素平均值：  [94.82406]
像素个数的最大值：  5029.0
像素个数的最小值：  0.0
1
2
3

2.3 基于灰度共生矩阵的纹理特征描述子；

​ 分析： 灰度共生矩阵指的是一种通过研究灰度的空间相关特性来描述纹理的常用方法。由于纹理是由灰度分布在空间位置上反复出现而形成的，因而在图像空间中相隔某距离的两像素之间会存在一定的灰度关系，即图像中灰度的空间相关特性。其求解方法：计算两两灰度值左右出现的个数。如下图：

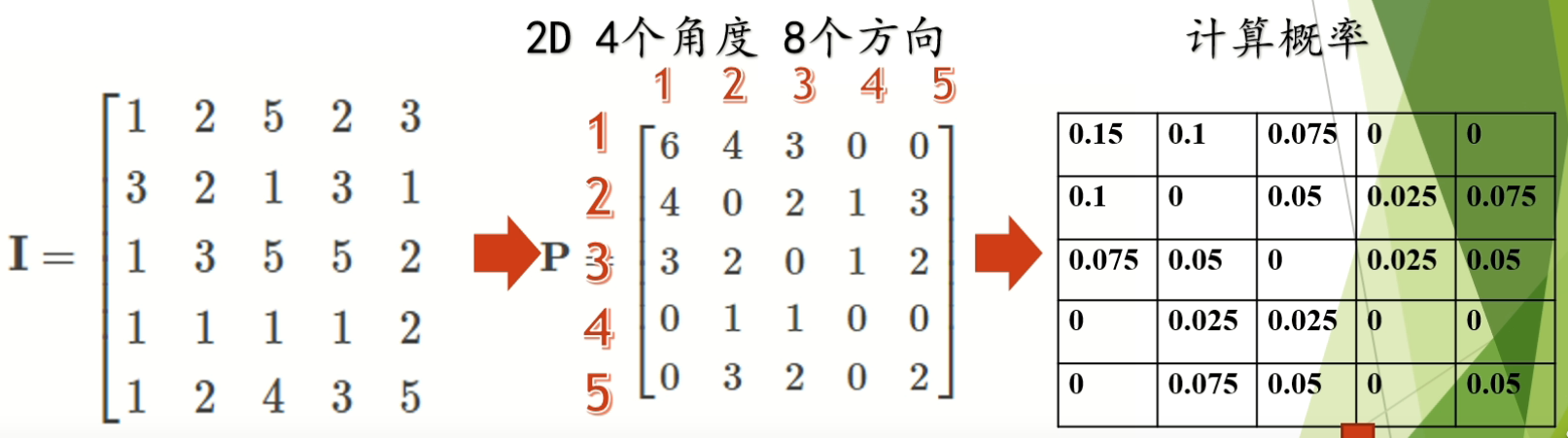
​ 左图是灰度图，右图为灰度共生矩阵。其计算如下：在左右方向上，灰度1-1出现的次数为6，灰度1-2出现的次数为4，灰度1-3出现的次数为3·······依次求得共生矩阵。

​ 灰度共生矩阵的描述子非常多，本文：
$$对比度Con=\sum _i\sum _j(i-j{)}^{2}P(i,j)$$

$$能量asm=\sum _i\sum _{j}P(i,j{)}^2$$

$$熵Ent=-\sum _i\sum _{j}P(i,j)logP(i,j)$$

$$逆方差H=\sum _i\sum _j\frac{P(i,j|d,\theta )}{1+(i-j{)}^2}$$

$$相关性Corr=\frac{{\sum }_i{\sum }_j(i,j)P(i,j)-{\mu }_x{\mu }_y}{{\sigma }_x{\sigma }_y}$$

​ 等7个特诊量。

​ 代码：

def maxGrayLevel(img):
    max_gray_level = 0
    (height, width) = img.shape
    print("图像的高宽分别为：height,width", height, width)
    for y in range(height):
        for x in range(width):
            if img[y][x] > max_gray_level:
                max_gray_level = img[y][x]
    print("max_gray_level:", max_gray_level)
    return max_gray_level + 1

# 获取灰度共生矩阵
def getGlcm(input, d_x, d_y):
    srcdata = input.copy()
    ret = [[0.0 for i in range(gray_level)] for j in range(gray_level)]
    (height, width) = input.shape

    max_gray_level = maxGrayLevel(input)
    # 若灰度级数大于gray_level，则将图像的灰度级缩小至gray_level，减小灰度共生矩阵的大小
    if max_gray_level > gray_level:
        for j in range(height):
            for i in range(width):
                srcdata[j][i] = srcdata[j][i] * gray_level / max_gray_level

    if d_x >= 0 or d_y >= 0:
        for j in range(height - d_y):
            for i in range(width - d_x):
                rows = srcdata[j][i]
                cols = srcdata[j + d_y][i + d_x]
                ret[rows][cols] += 1.0
    else:
        for j in range(height):
            for i in range(width):
                rows = srcdata[j][i]
                cols = srcdata[j + d_y][i + d_x]
                ret[rows][cols] += 1.0
    for i in range(gray_level):
        for j in range(gray_level):
            ret[i][j] /= float(height * width)

    return ret

# 获取特征
def feature_computer(p):
    # mean:均值
    # con:对比度反应了图像的清晰度和纹理的沟纹深浅。纹理越清晰反差越大对比度也就越大。
    # eng:熵（Entropy, ENT）度量了图像包含信息量的随机性，表现了图像的复杂程度。当共生矩阵中所有值均相等或者像素值表现出最大的随机性时，熵最大。
    # agm:角二阶矩（能量），图像灰度分布均匀程度和纹理粗细的度量。当图像纹理均一规则时，能量值较大；反之灰度共生矩阵的元素值相近，能量值较小。
    # idm:反差分矩阵又称逆方差，反映了纹理的清晰程度和规则程度，纹理清晰、规律性较强、易于描述的，值较大。
    # Auto_correlation：相关性
    mean = 0.0
    Con = 0.0
    Eng = 0.0
    Asm = 0.0
    Idm = 0.0
    Auto_correlation = 0.0
    std2 = 0.0
    std = 0.0
    for i in range(gray_level):
        for j in range(gray_level):
            mean += p[i][j] * i / gray_level ** 2
            Con += (i - j) * (i - j) * p[i][j]
            Asm += p[i][j] * p[i][j]
            Idm += p[i][j] / (1 + (i - j) * (i - j))
            Auto_correlation += p[i][j] * i * j
            if p[i][j] > 0.0:
                Eng += p[i][j] * math.log(p[i][j])
        for i in range(gray_level):
            for j in range(gray_level):
                std2 += (p[i][j] * i - mean) ** 2
        std = np.sqrt(std2)
    return mean, Asm, Con, -Eng, Idm, Auto_correlation, std


def test(image_name):
    img = cv2.imread(image_name)
    try:
        img_shape = img.shape
    except:
        print('imread error')
        return

    img = cv2.resize(img, (img_shape[1] // 2, img_shape[0] // 2), interpolation=cv2.INTER_CUBIC)
    # img = cv2.resize(img, dsize=(1000, 1000))
    print(img.shape)
    img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    plt.subplot(2, 2, 1)
    plt.title("原灰度图")
    plt.imshow(img_gray, cmap='gray')


    glcm_0 = getGlcm(img_gray, 1, 0)
    plt.subplot(2, 2, 2)
    plt.title("灰度共生矩阵图")
    plt.imshow(glcm_0)
    plt.show()
    mean, asm, con, eng, idm, Auto_correlation, std = feature_computer(glcm_0)
    return [mean, asm, con, eng, idm, Auto_correlation, std]


if __name__ == '__main__':
    [mean, asm, con, eng, idm, Auto_correlation, std] = test("data//Lenna.jpg")
    print("均值：", mean)
    print("能量： ", asm)
    print("对比度： ", con)
    print("熵：", eng)
    print("逆方差：", idm)
    print("相关性: ", Auto_correlation)
    print("标准差: ", std)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109

​ 结果：

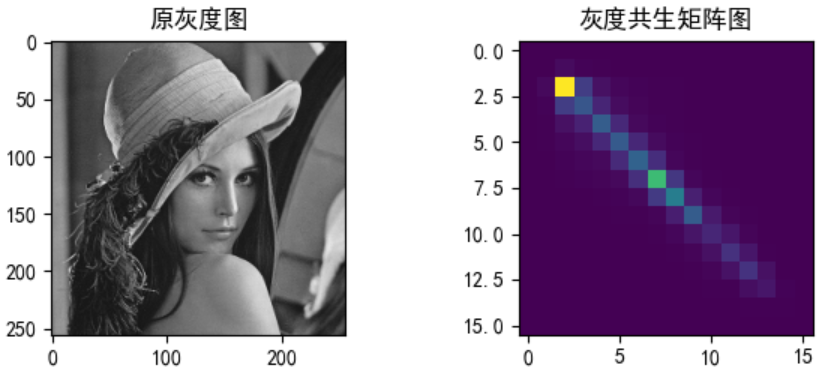
均值： 0.023376822471618652
能量：  0.04705131379887462
对比度：  1.5802154541015625
熵： 3.6640321056667453
逆方差： 0.7383503695439089
相关性:  44.634185791015625
标准差:  4.563554934281646
1
2
3
4
5
6
7

2. 4 图像的7个不变矩；

​ 分析： Hu矩值具有旋转、缩放、镜像和平移不变性，即图片经过旋转、缩放、平移变换后，其Hu矩值不变。这在图像识别中非常重要，例如：摄像头对一个物体进行摄像，那么根据距离的远近成像大小不同，就可以通过Hu矩值判断是同一个物体。可以通过cv2.HuMoment()方法来计算7个不变矩。

​ 代码：

def get_HuMoment(img):
    moments = cv2.moments(img)
    humoments = cv2.HuMoments(moments)
    # 因为直接计算出来的矩可能很小或者很大，因此取对数好比较,这里的对数底数为e,通过对数除法的性质将其转换为以10为底的对数，一般是负值，因此加一个负号将其变为正的
    humoments = -(np.log(np.abs(humoments))) / np.log(10)  # 同样建议取对数
    print("7个不变矩：\n", humoments)


if __name__ == '__main__':
    # t1 = datetime.now()
    img = cv2.imread("data//Lenna.jpg")
    img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    get_HuMoment(img_gray)
1
2
3
4
5
6
7
8
9
10
11
12
13

​ **结果：**计算的是Lenna.jpg图片的不变矩

7个不变矩：
 [[ 2.75925723]
 [ 7.78728719]
 [10.60653123]
 [10.36252463]
 [21.72074743]
 [14.25927953]
 [20.85097249]]
1
2
3
4
5
6
7
8

3. 对图像使用主成分法进行图像压缩。

​ 分析： PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分。

​ 代码：

img: np.ndarray = cv2.imread("data//Lenna.jpg")
img = img[:, :, 0]
imgShow(img, 1, 2, 1, "压缩前", isGray=True, isShow=False)
# 预处理
img = img / 255 - 0.5   # 灰度图 X 进行正规化  normalization
img_T = img.transpose()
Mat = img_T.dot(img)  # 得到 X * X_T
# 求 X * X_T 的前k大特征向量
eigvals, vecs = np.linalg.eig(Mat)  # 注意求出的eigvals是特征值，vecs是标准化后的特征向量
indexs = np.argsort(eigvals)
print(eigvals.shape)

# 编码矩阵 D 是前k大特征向量组成的矩阵(正交矩阵)——topk_evecs
k = 64
topk_evecs:np.ndarray = vecs[:,indexs[:-k-1:-1]]
print(topk_evecs.shape)

# X * D = 维度压缩后的图片信息——encode  （信息由 512 x 512 压缩为 512 x 64）
encode = img.dot(topk_evecs)

# 译码矩阵即 D_T
img_new = ((encode.dot(topk_evecs.transpose()) + 0.5) * 255).astype(np.uint8)  # 译码得到的新图片
print(img_new)
img_new[img_new < 0] = 0
img_new[img_new > 255] = 255
imgShow(img_new, 1, 2, 2, "压缩后", isGray=True, isShow=True
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

​ 结果：

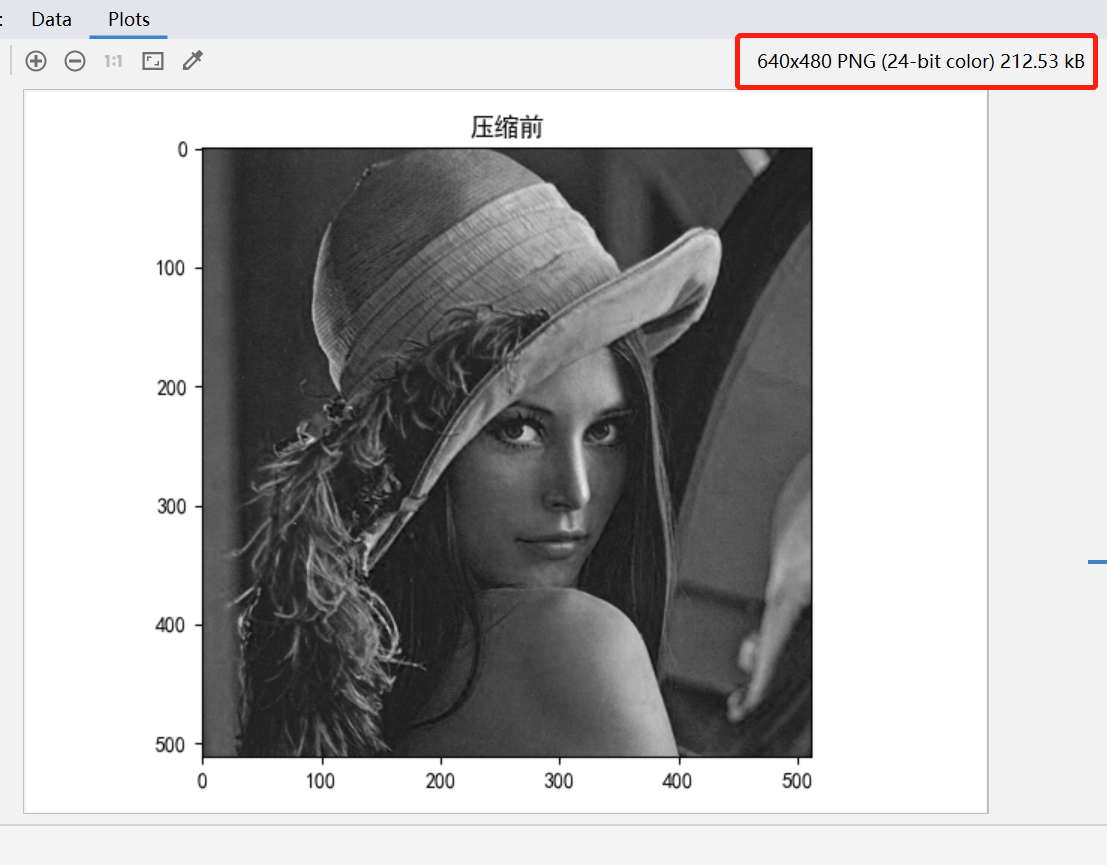
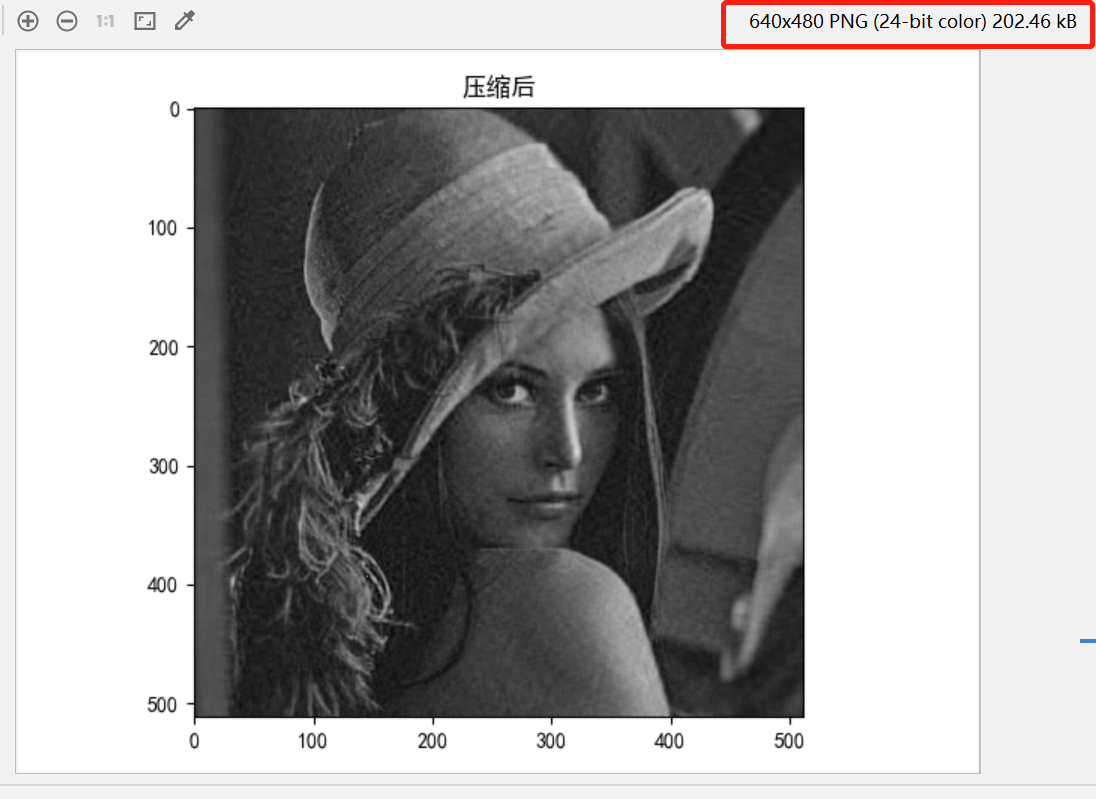
压缩前图片大小21kb, 压缩后202kb,因图片不一样，其压缩效果也不一样。