[C语言]CORDIC计算三角函数实验_cordic算法c语言

简介：

        CORDIC（Coordinate Rotation Digital Computer）算法即坐标旋转数字计算方法，是J.D.Volder1于1959年首次提出，主要用于三角函数、双曲线、指数、对数的计算。该算法通过基本的加和移位运算代替乘法运算，使得矢量的旋转和定向的计算不再需要三角函数、乘法、开方、反三角、指数等函数。(百度百科)

        CORDIC算法使用更适合计算机的运算来计算旋转，通过矢量旋转就可以得到三角函数、反三角函数的值，通过双曲旋转能计算双曲三角函数、开方、指数等，它的应用非常广泛，这里就只提关于Cordic计算三角函数的部分。

简单提一下原理：

首先推一下旋转的迭代公式，这里用复数乘法推。

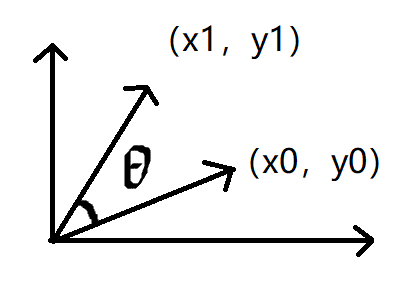
如图，矢量(x0,y0)逆时针旋转θ角度后得到(x1,y1)，

那么有 ,

根据公式

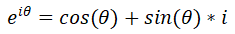
 以及 复数乘法加法的运算律得到

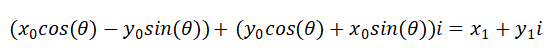
所以有

提出cos(θ)或者sin(θ)就得到了矢量旋转的迭代公式

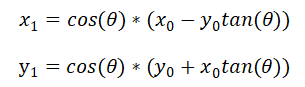
这里需要乘tan(θ)，试着把它变成移位运算，我们知道右移n位相当于乘以，这里用excel计算一下对应的角度值θ。

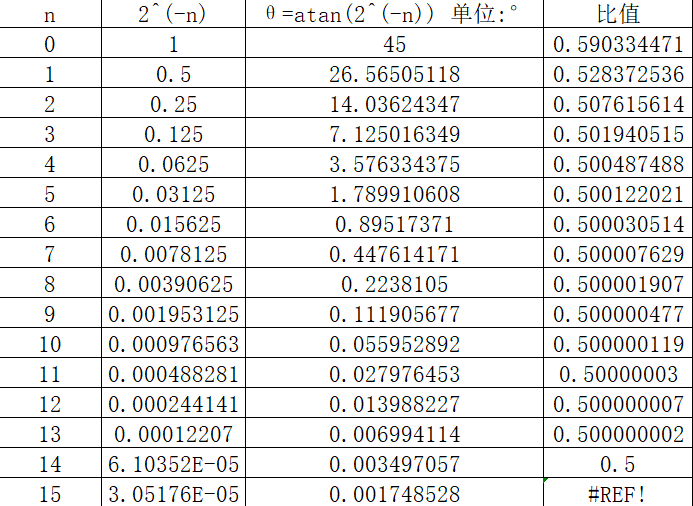
表中的角度值θ有两个良好的性质：

第一:将从0到15求和得到99.882°，这说明从0到15迭代的旋转范围在[-99.882°,99.882°]。

第二:，这是一个很好的性质，表格中上下两个角度的比值都接近0.5，如果输入角在[-90°,90°]间，旋转角度可以类似二分法那样去靠近输入角度。

现在可以用右移来代替乘tan(θ)，还剩一个乘cos(θ)需要处理，

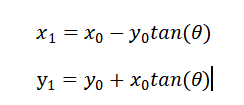
 把cos(θ)去掉，与真正的旋转相比少了一个拉伸，这也被称为伪旋转，如果迭代次数固定，那么拉伸系数也是固定的。

 

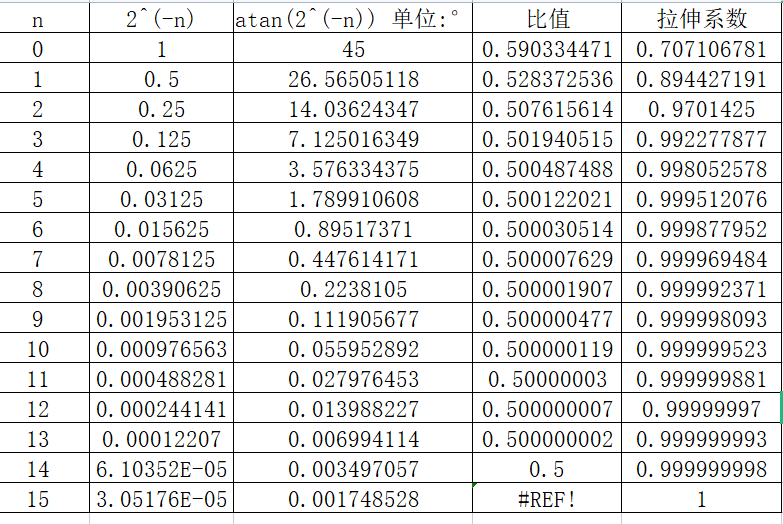
固定迭代16次，求出每次的拉伸系数再乘起来就得到了最终的拉伸系数K，在excel中算出K=0.607252935。

(顺便提一下，提出sin的公式的k=4.56846E-37,这非常小，写代码的话不好搞。)

得到k的值后，就能计算向量旋转的近似值了，比如求向量(1,0)逆时针旋转θ度后的向量，可以用(1,0)伪旋转迭代16次后乘以k得到近似值，优化一下，k和(1,0)都是固定值，把k*(1,0)先算得到新的初值，那就变成:用(k,0)伪旋转迭代16次。

得到旋转后的向量再根据下面的公式就能求三角函数了。

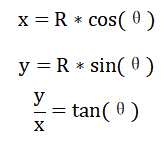
测试代码：

#include <stdio.h>
#include <windows.h>
#include <math.h>
#define abs_h(a) (a>0.0?a:-(a)) //绝对值
#define Pi 3.1415927
 
int Ang[16]={4500000,2656505,1403624,712502,357633,178991,89517,44761,22381,11191,5595,2798,1399,699,350,175};
int cos_core(int a);
int atan2_core(int y,int x);
volatile double a[512];
volatile int a_int[512];
volatile double x[512];
volatile double y[512];
volatile int x_int[512];
volatile int y_int[512];	
int main(void)
{
    LARGE_INTEGER s,e,f;
    volatile int i;
    double DT;//时间 单位ms
    double Err;//误差(与math的函数的误差)
    QueryPerformanceFrequency(&f);//获得频率
    Err=0.0;
    for(i=0;i<512;i++)
    {
        a[i]=Pi/256.0*i-Pi;//2pi分割成512份，范围(-180°~180°)
        a_int[i]=a[i]*100000.0*180.0/Pi;
        Err+=abs_h(cos(a[i])-cos_core(a_int[i])/100000.0);//计算误差
        //printf("------------\r\n");
        //printf("cos(%f)=%f\r\n",a[i],cos(a[i]));
        //printf("cos_core(%d)=%f\r\n",a_int[i],cos_core(a_int[i])/100000.0);
        //printf("误差:%f\r\n",abs_h(cos(a[i])-cos_core(a_int[i])/100000.0));
    }
    printf("cos_core平均误差:%f\r\n",Err/512.0);
 
    Err=0.0;
    for(i=0;i<512;i++)
    {
        x[i]=cos(a[i]);
				y[i]=sin(a[i]);
        x_int[i]=x[i]*100000.0;
				y_int[i]=y[i]*100000.0;
        Err+=abs_h(atan2(y[i],x[i])*180.0/Pi-atan2_core(y_int[i],x_int[i])/100000.0);//计算误差
        //printf("------------\r\n");
        //printf("atan2(%f,%f)=%f度\r\n",y[i],x[i],atan2(y[i],x[i])*180.0/Pi);
        //printf("atan2_core(%d,%d)=%f度\r\n",y_int[i],x_int[i],atan2_core(y_int[i],x_int[i])/100000.0);
		//printf("误差:%f度\r\n",abs_h(atan2(y[i],x[i])*180.0/Pi-atan2_core(y_int[i],x_int[i])/100000.0));
    }
    printf("atan2_core平均误差:%f度\r\n",Err/512.0);
 
    
    printf("频率:%d\r\n",f.QuadPart);
 
	QueryPerformanceCounter(&s);
    for(i=0;i<500000;i++)
    {
        cos_core(a_int[i&0x1ff]);//0x1ff=512-1
    }
	QueryPerformanceCounter(&e);
	DT=(0.0+e.QuadPart-s.QuadPart)/(0.001*f.QuadPart);
    printf("cos_core耗时=%fms\r\n",DT);
 
 
	QueryPerformanceCounter(&s);
    for(i=0;i<500000;i++)
    {
       cos(a[i&0x1ff]);//0x1ff=512-1
    }
	QueryPerformanceCounter(&e);
	DT=(0.0+e.QuadPart-s.QuadPart)/(0.001*f.QuadPart);
    printf("cos耗时=%fms\r\n",DT);
 
 
	QueryPerformanceCounter(&s);
    for(i=0;i<500000;i++)
    {
        atan2_core(y_int[i&0x1ff],x_int[i&0x1ff]);//0x1ff=512-1
    }
	QueryPerformanceCounter(&e);
	DT=(0.0+e.QuadPart-s.QuadPart)/(0.001*f.QuadPart);
    printf("atan2_core耗时=%fms\r\n",DT);
 
 
	QueryPerformanceCounter(&s);
    for(i=0;i<500000;i++)
    {
       atan2(y[i&0x1ff],x[i&0x1ff]);//0x1ff=512-1
    }
	QueryPerformanceCounter(&e);
	DT=(0.0+e.QuadPart-s.QuadPart)/(0.001*f.QuadPart);
    printf("atan2耗时=%fms\r\n",DT);
    return 0;
}
int cos_core(int a)
{
	char i;
	int x=30363,y=0,temp;//18次迭代,先连续2次45°旋转作为90°旋转,输入角度范围扩大至[-189.8812173,189.8812173]
	if(a>=18988122||a<=-18988122)
	 return 0;
     
	if(a>=0)
	{
		temp=x-y;
		y+=x;
		x=temp;		
		temp=x-y;
		y+=x;
		x=temp;
		a-=9000000;
	}
	else if(a<0)
	{
		temp=x+y;
		y-=x;
		x=temp;		
		temp=x+y;
		y-=x;
		x=temp;
		a+=9000000;
	}
    
	for(i=0;i<16;i++)
	{
	 if(a>=0)
	 {
		temp=x-(y>>i);
		y+=(x>>i);
		x=temp;		
		a-=Ang[i];		  
	 }
	 else if(a<0)
	 {
		temp=x+(y>>i);
		y-=(x>>i);
		x=temp;		
		a+=Ang[i];	 
	 }
	}
	return x;
    
}
int atan2_core(int y,int x)
{
	char i;
	int temp,a;
	a=0;
	if(y<0)
	{
		temp=x-y;
		y+=x;
		x=temp;		
		temp=x-y;
		y+=x;
		x=temp;
		a-=9000000;
	}
	else if(y>0)
	{
		temp=x+y;
		y-=x;
		x=temp;		
		temp=x+y;
		y-=x;
		x=temp;
		a+=9000000;
	}
	else
	{
		if (x<0)
			return 18000000;
		else //两个情况，但atan2(0.0,0.0)返回0.0，所以直接返回0
			return 0;
	}
	for(i=0;i<16;i++)
	{
	 if(y<0)
	 {
		temp=x-(y>>i);
		y+=(x>>i);
		x=temp;		
		a-=Ang[i];		  
	 }
	 else if(y>0)
	 {
		temp=x+(y>>i);
		y-=(x>>i);
		x=temp;		
		a+=Ang[i];	 
	 }
	 else
	  return a;
	}
	return a;
}

输出：

        时间：我在单片机平台上复制了一份一样的代码，PC的输出结果与单片机的输出结果截然不同。

PC输出：

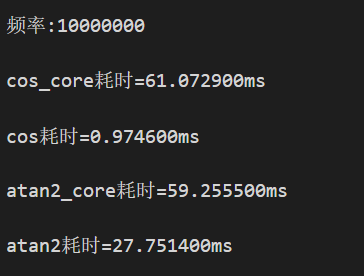
单片机(STM32F103)输出：

经过对比：单片机上CORDIC比math的三角函数快很多，PC上math的三角函数比CORDIC快很多。两个平台在许多方面有巨大差异，不清楚是什么原因导致了这种情况。

误差：

(这里的误差是以math的三角函数输出值为参考,两者相减的绝对值作为误差)

在这方面，PC与单片机的输出结果相同：

反正切atan2:

余弦:

观察到cos(180°)、cos(0°)等的输出超出了范围，得限制一下输出，其他看起来感觉还凑合，我会在单片机平台上使用它。

如果按照上面代码来运行，旋转角度不会与输入角度相等。在我这个思路中，初值固定，所以迭代次数也固定，就算旋转角度早已与输入重合，它也要走完剩下的。当然这是有解决办法的，也有很多地方可以优化，我这写的比较粗糙，我自己凑合着用。