【深度学习】激活函数和损失函数_损失函数和激活函数在神经网络中的位置

4.3 激活函数

作用：

当神经网络中上一层的输出直接作为下一层的输入时，每层之间的关系是线性关系，即相当于f(x)=x，此时神经网络的拟合能力较弱。为了使得神经网络有更好的拟合能力，在每一层网络之间加入了激活函数（非线性）来使得不同层网络之间的关系变为非线性，从而使网络有更好的拟合能力。

常用的激活函数有Sigmoid、tanh，ReLU、leaky ReLU等。除此以外还有线性激活函数如Linear。

激活函数的选取十分重要，不同的激活函数有不同的特点。选取不当可能会导致梯度变得非常小，就是通常所说的梯度消失问题。另外还存在一种相反的问题，就是梯度爆炸（不常见），当梯度值过大时，网络会变得非常不稳定。

---

4.3.1 Sigmoid

包：torch.nn.Sigmoid

计算公式：

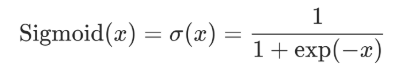
函数图像：

特点：

• 函数的值在0到1之间
• 适合处理二分类问题
• 计算较为复杂，因为要处理指数问题
• 在深度神经网络中梯度反向传递时容易导致梯度消失（梯度爆炸爆炸发生的概率非常小）
• 不是zero-centered，只有正数输出，所以会导致zigzag现象

---

4.3.2 tanh

包:torch.nn.Tanh

计算公式：

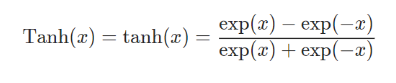
函数图像：

特点：

• 函数的值在-1到1之间
• 除二分类问题外，在任何时候该函数处理问题的能力都优于sigmoid函数
• 有饱和区域，是软饱和，在大的正数和负数作为输入的时候，梯度就会趋向于零（梯度消失），使神经元更新速率下降

---

4.3.3 ReLU

包：torch.nn.ReLU(inplace=False)

函数：

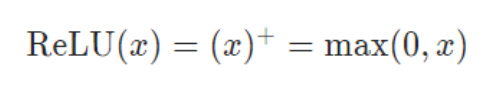
函数图像：

特点：

• CNN中常用，对正数原样输出，负数直接置零。
• 在正数不饱和，在负数硬饱和。
• ReLU计算上比sigmoid或者tanh更省计算量，因为不用算幂，因而收敛较快。但是非zero-centered。
• 在负数区域容易出现梯度消失问题，在大的正数区域容易出现梯度爆炸问题。
• ReLU在负数区域被kill的现象叫做Dead ReLU Problem（神经元坏死现象），这样的情况下，有人通过初始化的时候用一个稍微大于零的数比如0.01来初始化神经元，从而使得ReLU更偏向于激活而不是死掉，但是这个方法是否有效有争议。
  • dead ReLU problem 最直观的结果就是，输入ReLU中的值如果存在负数，则最终经过ReLU之后变成0，极端情况下是输入ReLU的所有值全都是负数，则ReLU activated之后的结果均为0。
  • 当神经元中的大多数返回零输出时，梯度在反向传播期间无法流动，并且权重不会更新。最终，大部分网络变得不活跃，无法进一步学习。

---

4.3.4 LeakyReLU

包：torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)

函数

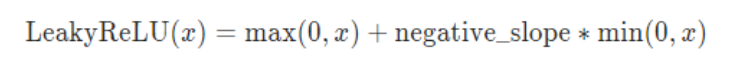
或者

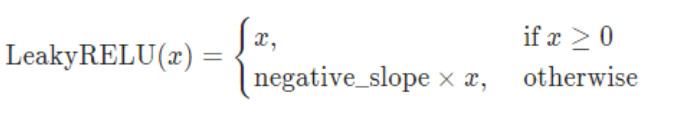
函数图像：

参数

• negative_slope ：控制负斜率的角度。默认值:1e-2
• inplace：可以选择就地执行操作。默认值:False

特点：

• 为了解决上述的dead ReLU现象。在小于0时选择一个数，让负数区域不在饱和死掉。
• 这里的斜率都是确定的，默认0.01。

---

4.3.5 PReLU

包：torch.nn.PReLU( num_parameters = 1 , init = 0.25 , device = None , dtype = None )

函数：

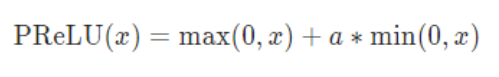
或者

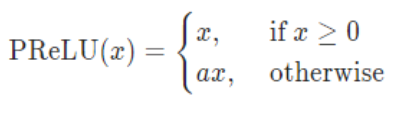
函数图像：

参数：

• num_parameters（int）：要学习的a数量。尽管它以int作为输入，但只有两个值是合法的：1或输入时的通道数。默认值：1
• init（float）：a的初始值。默认值：0.25。

特点：

• 为了获得良好的性能，在学习a时不应使用重量衰减。
• 通道尺寸是输入的第二尺寸。当输入dims < 2时，则没有通道dim，通道数 = 1。

---

4.4 损失函数

用于度量神经网络的输出的预测值与实际值之间的差距的一种方式。

为卷积核的参数设置梯度，利用梯度下降可以对更新卷积核的参数提供一定的依据（反向传播）。

回归损失函数：

• 均方差（Mean Squared Error，MSE）
• 平均绝对误差（Mean Absolute Error Loss，MAE）

分类损失函数：

• 对数损失函数LogLoss
• 交叉熵损失函数CrossEntropyLoss

逻辑回归就是使用对数损失函数来进行二分类任务，

softmax回归是逻辑回归的推广，

softmax回归使用交叉熵损失函数来进行多分类任务。

---

4.4.1 L1Loss均绝对误差

包：torch.nn.L1Loss(size_average=None, reduce=None, reduction='mean')

函数：

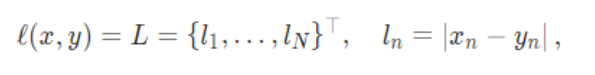
两种计算的方式

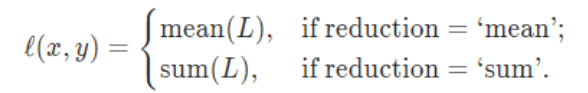
即均值和求和（默认均值）。

函数图像

特点：（转载于https://www.cnblogs.com/wangguchangqing/p/12021638.html）

• MSE的函数曲线光滑、连续，处处可导，便于使用梯度下降算法，是一种常用的损失函数。 而且，随着误差的减小，梯度也在减小，这有利于收敛，即使使用固定的学习速率，也能较快的收敛到最小值。
• 当y和f(x)也就是真实值和预测值的差值大于1时，会放大误差；而当差值小于1时，则会缩小误差，这是*方运算决定的。MSE对于较大的误差（>1）给予较大的惩罚，较小的误差（<1）给予较小的惩罚。也就是说，对离群点比较敏感，受其影响较大。
• 如果样本中存在离群点，MSE会给离群点更高的权重，这就会牺牲其他正常点数据的预测效果，最终降低整体的模型性能。 如下图：
• 

# 输入，需要的输入类型是float类型
input = torch.tensor([1, 2, 3], dtype=float)
# 目标
target = torch.tensor([1, 2, 5], dtype=float)

# 损失函数，可选参数有两个：mean, sum
# mean：默认，求差后求和在除以个数
# sum：求差后求和
loss1 = L1Loss(reduction="mean")
loss2 = L1Loss(reduction="sum")
result1 = loss1(input, target)
result2 = loss2(input, target)
print(result1)  # tensor(0.6667, dtype=torch.float64) 说明：((1 - 1) + (2 - 2) + (5 - 3)) / 3 = 0.6667
print(result2)  # tensor(2., dtype=torch.float64) 说明：((1 - 1) + (2 - 2) + (5 - 3)) = 2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14

---

4.4.2 MSELoss均方误差

包：torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')

函数：

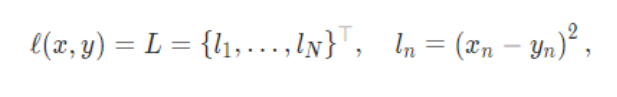
两种计算方式：

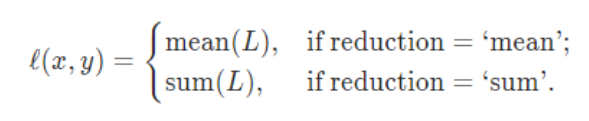
函数图像：

特点：

• MAE曲线连续，但是在y−f(x)=0y−f(x)=0处不可导。而且 MAE 大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的。这不利于函数的收敛和模型的学习。但是，无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健性的解。
• 相比于MSE，MAE有个优点就是，对于离群点不那么敏感。因为MAE计算的是误差y−f(x)的绝对值，对于任意大小的差值，其惩罚都是固定的。
• 针对上面带有离群点的数据，MAE的效果要好于MSE。
  

---

4.4.3 MSE和MAE的选择

• 从梯度的求解以及收敛上，MSE是由于MAE的。MSE处处可导，而且梯度值也是动态变化的，能够快速的收敛；而MAE在0点处不可导，且其梯度保持不变。对于很小的损失值其梯度也很大，在深度学习中，就需要使用变化的学习率，在损失值很小时降低学习率。
• 对离群（异常）值得处理上，MAE要明显好于MSE。
• 如果离群点（异常值）需要被检测出来，则可以选择MSE作为损失函数；如果离群点只是当做受损的数据处理，则可以选择MAE作为损失函数。

总之，MAE作为损失函数更稳定，并且对离群值不敏感，但是其导数不连续，求解效率低。另外，在深度学习中，收敛较慢。MSE导数求解速度高，但是其对离群值敏感，不过可以将离群值的导数设为0（导数值大于某个阈值）来避免这种情况。在某些情况下，上述两种损失函数也可能都不满足需求。

---

4.4.3 CrossEntropyLoss交叉熵

包：torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=- 100, reduce=None, reduction='mean', label_smoothing=0.0)

函数：

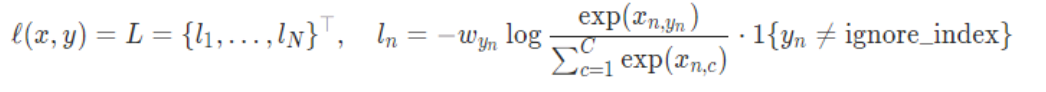
两种计算方式：

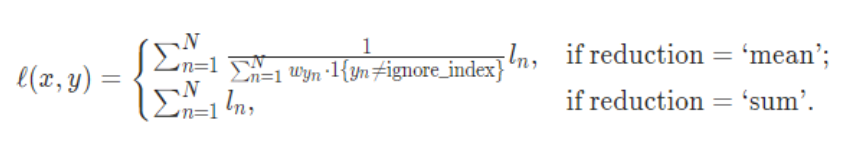
该函数结合了nn.LogSoftmax()和nn.NLLLoss()函数
    1、Softmax后的数值都在0~1之间，所以ln之后值域是负无穷到0。
    2、然后将Softmax之后的结果取log，将乘法改成加法减少计算量，同时保障函数的单调性

代码示例：

import torch
import torchvision.datasets
from torch import nn
from torch.nn import L1Loss, Sequential, Conv2d, MaxPool2d, Flatten, Linear
from torch.utils.data import DataLoader


class MyNN(nn.Module):

    def __init__(self) -> None:
        super().__init__()
        self.sequential = Sequential(
            Conv2d(3, 32, 5, padding=2),
            MaxPool2d(2),
            Conv2d(32, 32, 5, padding=2),
            MaxPool2d(2),
            Conv2d(32, 64, 5, padding=2),
            MaxPool2d(2),
            Flatten(),
            Linear(1024, 64),
            Linear(64, 10)
        )

    def forward(self, x):
        x = self.sequential(x)
        return x


dataset = torchvision.datasets.CIFAR10("dataset", transform=torchvision.transforms.ToTensor())
dataLoader = DataLoader(dataset, batch_size=1)

demo_loss = MyNN()
# 交叉商
loss = nn.CrossEntropyLoss()
step = 0
for data in dataLoader:
    imgs, targets = data
    output = demo_loss(imgs)
    print(output)
    print(targets)
    # 计算实际输出和目标输出之间的差距
    result_loss = loss(output, targets)
    print(result_loss)

    # 反向传播，为更新数据提供一定的依据。会在这一步算出一个梯度
    result_loss.backward()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

---

注：本博客只用于人笔记记录，内容来自网络整理