异常检测（四）--- 基于相似度的方法_图像相似度算法 异常检测

四、基于相似度的方法

1、概述

“异常”通常是一个主观的判断，什么样的数据被认为是“异常”的，需要结合业务背景和环境来具体分析确定。

实际上，数据通常嵌入在大量的噪声中，而我们所说的“异常值”通常指具有特定业务意义的那一类特殊的异常值。噪声可以视作特性较弱的异常值，没有被分析的价值。噪声和异常之间、正常数据和噪声之间的边界都是模糊的。异常值通常具有更高的离群程度分数值，同时也更具有可解释性。

在普通的数据处理中，我们常常需要保留正常数据，而对噪声和异常值的特性则基本忽略。但在异常检测中，我们弱化了“噪声”和“正常数据”之间的区别，专注于那些具有有价值特性的异常值。在基于相似度的方法中，主要思想是异常点的表示与正常点不同。

2、基于距离的度量

基于距离的方法是一种常见的适用于各种数据域的异常检测算法，它基于最近邻距离来定义异常值。此类方法不仅适用于多维数值数据，在其他许多领域，例如分类数据，文本数据，时间序列数据和序列数据等方面也有广泛的应用。

基于距离的异常检测有这样一个前提假设，即异常点的近邻距离要远大于正常点。解决问题的最简单方法是使用嵌套循环。 第一层循环遍历每个数据，第二层循环进行异常判断，需要计算当前点与其他点的距离，一旦已识别出多于 个数据点与当前点的距离在 之内，则将该点自动标记为非异常值。

这样计算的时间复杂度为O(N^2)，当数据量比较大时，这样计算是及不划算的。 因此，需要修剪方法以加快距离计算。

2.1 基于单元的方法

在基于单元格的技术中，数据空间被划分为单元格，单元格的宽度是阈值D和数据维数的函数。具体地说，每个维度被划分成宽度最多为 (D/(2sqrt(d)))单元格。在给定的单元以及相邻的单元中存在的数据点满足某些特性，这些特性可以让数据被更有效的处理。

以二维情况为例，此时网格间的距离为(D/(2sqrt(d)))，需要记住的一点是，网格单元的数量基于数据空间的分区，并且与数据点的数量无关。这是决定该方法在低维数据上的效率的重要因素，在这种情况下，网格单元的数量可能不多。 另一方面，此方法不适用于更高维度的数据。对于给定的单元格，其L1邻居被定义为通过最多1个单元间的边界可从该单元到达的单元格的集合。请注意，在一个角上接触的两个单元格也是L1邻居。L2邻居是通过跨越2个或3个边界而获得的那些单元格。 上图中显示了标记为X 的特定单元格及其L1和L2邻居集。 显然，内部单元具有8个L1邻居和40个L2邻居。 然后，可以立即观察到以下性质:

• 单元格中两点之间的距离最多为D/2 。
• 一个点与L1邻接点之间的距离最大为D。
• 一个点与它的 Lr邻居(其中r > 2)中的一个点之间的距离至少为F。

唯一无法直接得出结论的是L2中的单元格。 这表示特定单元中数据点的不确定性区域。对于这些情况，需要明确执行距离计算。同时，可以定义许多规则，以便立即将部分数据点确定为异常值或非异常值。 规则如下：

• 如果一个单元格中包含超过k 个数据点及其L1 邻居，那么这些数据点都不是异常值。
• 如果单元A 及其相邻L1 和L2中包含少于k个数据点，则单元A中的所有点都是异常值。

此过程的第一步是将部分数据点直接标记为非异常值（如果由于第一个规则而导致它们的单元格包含k个点以上）。 此外，此类单元格的所有相邻单元格仅包含非异常值。 为了充分利用第一条规则的修剪能力，确定每个单元格及其L1邻居中点的总和。 如果总数大于k，则所有这些点也都标记为非离群值。

2.2 基于索引的方法

对于一个给定数据集，基于索引的方法利用多维索引结构(如R树\k-d树)来搜索每个数据对象A在半径D范围 内的相邻点。设 M是一个异常值在其 D-邻域内允许含有对象的最多个数，若发现某个数据对象A的 D-邻域内出现M+1 甚至更多个相邻点， 则判定对象A不是异常值。该算法时间复杂度在最坏情况下为O(kN^2) 其中 k是数据集维数，N是数据集包含对象的个数。该算法在数据集的维数增加时具有较好的扩展性，但是时间复杂度的估算仅考虑了搜索时间，而构造索引的任务本身就
需要密集复杂的计算量。

3、基于密度的度量

基于密度的算法主要有局部离群因子(LocalOutlierFactor,LOF)，以及LOCI、CLOF等基于LOF的改进算法。下面我们以LOF为例来进行详细的介绍和实践。

基于距离的检测适用于各个集群的密度较为均匀的情况。在下图中，离群点B容易被检出，而若要检测出较为接近集群的离群点A，则可能会将一些集群边缘的点当作离群点丢弃。而LOF等基于密度的算法则可以较好地适应密度不同的集群情况。

那么，这个基于密度的度量值是怎么得来的呢？还是要从距离的计算开始。类似k近邻的思路，首先我们也需要来定义一个“k-距离”。

3.1 k-距离（k-distance§）：

对于数据集D中的某一个对象o，与其距离最近的k个相邻点的最远距离表示为k-distance§，定义为给定点p和数据集D中对象o之间的距离d(p,o)，满足:

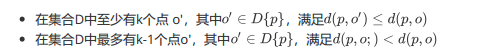
直观一些理解，就是以对象o为中心，对数据集D中的所有点到o的距离进行排序，距离对象o第k近的点p与o之间的距离就是k-距离。

3.2 k-邻域（k-distance neighborhood）：

由k-距离，我们扩展到一个点的集合——到对象o的距离小于等于k-距离的所有点的集合，我们称之为k-邻域：

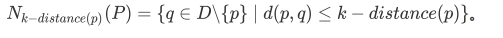
在二维平面上展示出来的话，对象o的k-邻域实际上就是以对象o为圆心、k-距离为半径围成的圆形区域。就是说，k-邻域已经从“距离”这个概念延伸到“空间”了。

3.3 可达距离（reachability distance）：

3.4 局部可达密度（local reachability density）：

我们可以将“密度”直观地理解为点的聚集程度，就是说，点与点之间距离越短，则密度越大。在这里，我们使用数据集D中给定点p与对象o的k-邻域内所有点的可达距离平均值的倒数（注意，不是导数）来定义局部可达密度。

给定点p的局部可达密度计算公式为：

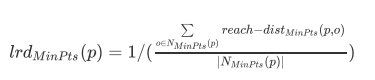
由公式可以看出，这里是对给定点p进行度量，计算其邻域内的所有对象o到给定点p的可达距离平均值。给定点p的局部可达密度越高，越可能与其邻域内的点 属于同一簇；密度越低，越可能是离群点。

3.5 局部异常因子：

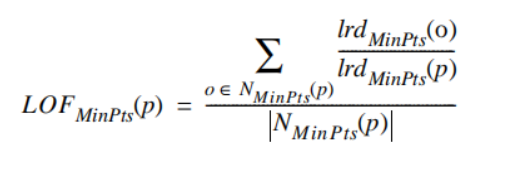
最终得出的LOF数值，就是我们所需要的离群点分数。在sklearn中有LocalOutlierFactor库，可以直接调用。下面来直观感受一下LOF的图像呈现效果。

LocalOutlierFactor库可以用于对单个数据集进行无监督的离群检测，也可以基于已有的正常数据集对新数据集进行新颖性检测。在这里我们进行单个数据集的无监督离群检测。