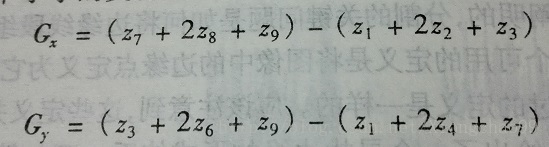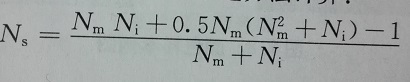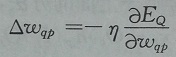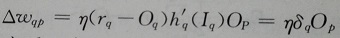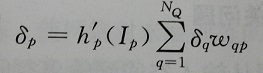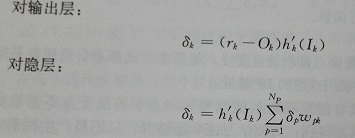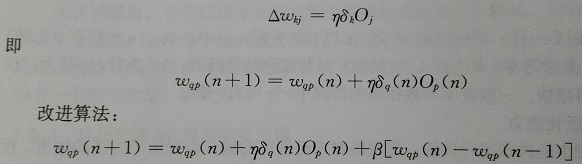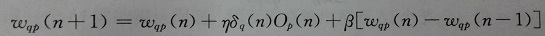- 1【模拟赛】沼泽地(插头DP)_小红闯沼泽地
- 2基于YOLOv8的船舶目标检测系统(Python源码+Pyqt6界面+数据集)
- 3Ubuntu18.04 安装Docker-Compose_ubuntu18.04安装docker-compose1.25
- 4Druid多数据源配置(Datasurce动态切换)_druiddatasourcebuilder
- 5Java后台微信点餐小程序开发最新版笔记,Springboot+Mysql+Freemarker+Bootstrap+微信小程序实现扫码点餐小程序,包含语音提示,微信消息推送,网页管理后台_java扫码点餐
- 6python点餐系统代码_Python从菜鸟到进阶,设计模式必须要会!
- 7【C++中的STL】常用算法2——排序算法
- 8java开发必会技能_java相关技能
- 9Javaweb 编码过滤器无效_filter validatorfilter was not registered
- 10【状压DP】状态压缩动态规划入门超详解
图像处理基础_灰度sk下标k是什么意思
赞
踩
第一章 数字图像基本知识
1、 彩色图像、灰度图像、二值图像和索引图像区别?
答:(1)彩色图像,每个像素通常是由红(R)、绿(G)、蓝(B)三个分量来表示的,分量介于(0,255)。M、N分别表示图像的行列数,三个M x N的二维矩阵分别表示各个像素的R、G、B三个颜色分量。RGB图像的数据类型一般为8位无符号整形,通常用于表示和存放真彩色图像,当然也可以存放灰度图像。(2)灰度图像(gray image)是每个像素只有一个采样颜色的图像,这类图像通常显示为从最暗黑色到最亮的白色的灰度。灰度图像与黑白图像不同,在计算机图像领域中黑白图像只有黑色与白色两种颜色;用于显示的灰度图像通常用每个采样像素8位的非线性尺度来保存,这样可以有256级灰度(如果用16位,则有65536级)。
(3)二值图像(binary image),即一幅二值图像的二维矩阵仅由0、1两个值构成,“0”代表黑色,“1”代白色。由于每一像素(矩阵中每一元素)取值仅有0、1两种可能,计算机存储的二值化图像用0和255来表示。二值图像通常用于文字、线条图的扫描识别(OCR)和掩膜图像的存储。
(4)索引图像是为了减少RGB真彩色存储容量而提出的,它的实际像素点和灰度图一样用二维数组存储,只不过灰度值的意义在于表示颜色表索引位置;而颜色表是指颜色索引矩阵MAP,MAP的大小由存放图像的矩阵元素值域决定,如矩阵元素值域为[0,255],则MAP矩阵的大小为256×3,MAP中每一行的三个元素分别指定该行对应颜色的红、绿、蓝单色值。
如某一像素的灰度值为64,则该像素的颜色值就是MAP中的第64行的RGB组合。也就是说,图像在屏幕上显示时,每一像素的颜色由存放在矩阵中该像素的灰度值作为索引通过检索颜色索引矩阵MAP得到。索引图像一般用于存放色彩要求比较简单的图像,如Windows中色彩构成比较简单的壁纸多采用索引图像存放,如果图像的色彩比较复杂,就要用到RGB真彩色图像。
2、奈奎斯特采样定理
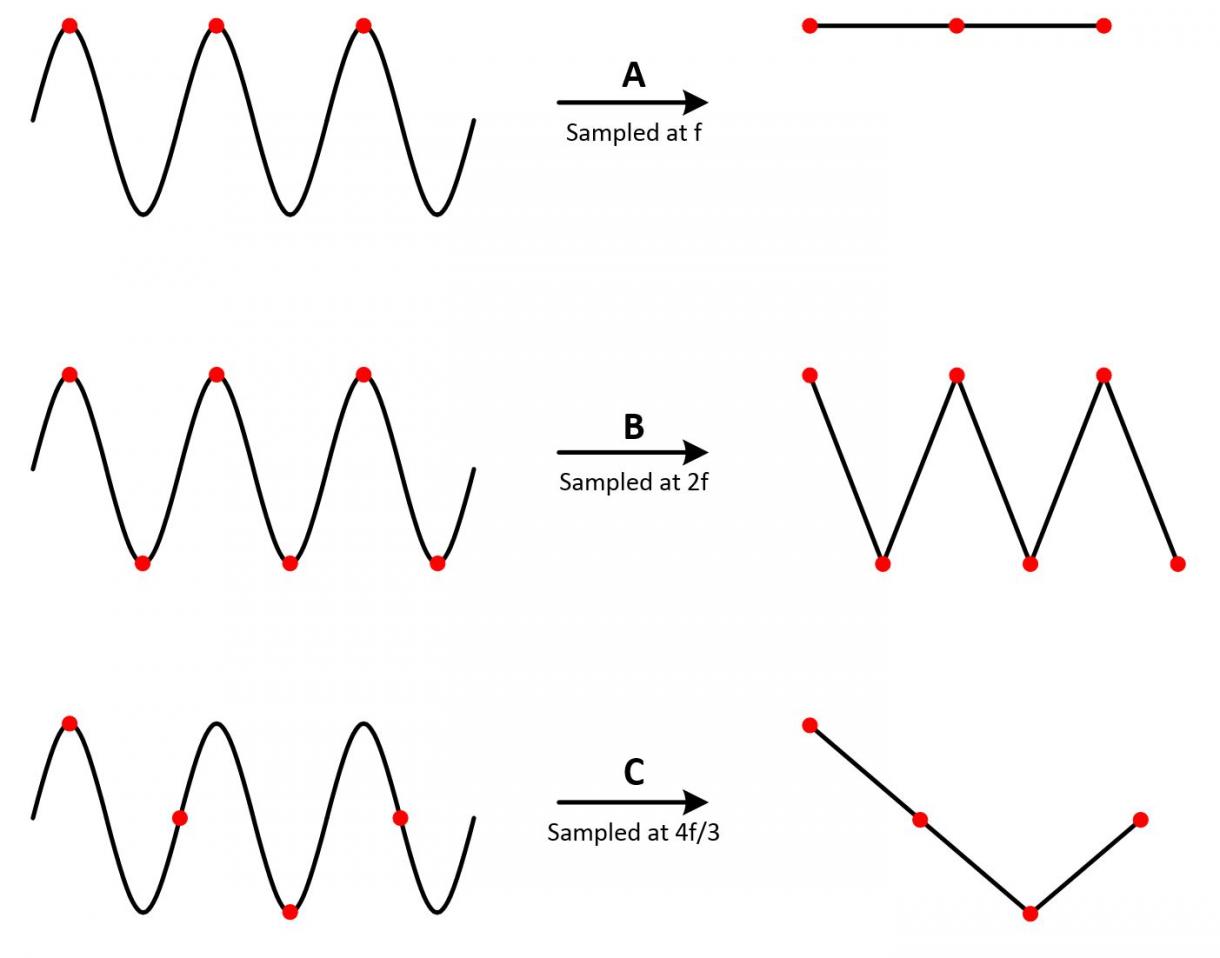
答:奈奎斯特采样定理解释了采样率和所测信号频率之间的关系,即采样率fs必须大于被测信号最高频率分量fmax的两倍,fmax频率通常被称为奈奎斯特频率,公式:
fs>2*fmax;
至于奈奎斯特采样定理成立的原因,可见下图:
第二章 图像增强
1、图像增强包括哪些?
答:(1)图像增强主要分为空间域增强方法和频域增强方法。
空间域就是指图像本身,频域指图像经过傅里叶变换的信号;
(2)空间域图像增强操作很多:
灰度变换:如二值化、图像反转(255-grayValue)、对数变换(增大像素的灰度值,尤其对源图的暗像素效果明显,参见对数曲线)、反对数变换(减小像素灰度值,尤其对亮像素效果明显,参见反对数曲线)、幂次变换(又叫伽马校正,其可以增大或减少像素灰度值,具有变换程度与指数γ大小有关,参见幂函数曲线)、分段线性函数变换(包括对比拉伸、灰度切割、位图切割);
直方图处理(直方图均衡化、直方图局部增强);
算数逻辑操作增强(图像减法处理、图像平均处理);
平滑滤波、线性滤波、统计排序滤波、均值滤波、中值滤波等滤波;
锐化处理(拉普拉斯算子锐化、梯度法锐化);
等等,都是空间域图像增强方法。
2、灰度直方图
答:灰度直方图是横坐标为灰度级、纵坐标为像素个数的直方图,用于表示每个灰度范围内的像素个数;
归一化灰度直方图:将灰度直方图的纵坐标值除以像素总数,产生的新直方图即是。
3、直方图均衡化与应用
答:(1)直方图均衡化:就是通过变换函数,使得图像的灰度分布较为均匀,将灰度值集中的部分均匀分散到整个灰度范围,使得直方图的各个灰度级y轴较为平坦。从而实现图像增强,如较暗的图片变得较为明亮,过亮的图片变的正常,从而利于观察识别。
(2)均衡化的变换函数:就是一个映射函数,必须满足两个条件:1)一个单值单增函数;2)映射后灰度范围不变。实际中常用累积分布函数。累积分布函数如下定义:
①先求当前灰度级的累计概率(即当前灰度级以及小于当前灰度级的像素个数和在图像中的比例):

Sk是当前像素值的累计概率,k是当前像素的像素值,n是图像中像素个数的总和,nj是当像素值等于j的像素个数,L是图像中可能的灰度级总数。
②求当前像素的映射像素值:
映射函数g=最大灰度值*Sk;(例如最大灰度值为255,则g=255*Sk)
(3)缺点:
1)变换后图像的灰度级减少,某些细节消失;
2)某些图像,如直方图有高峰,经处理后对比度不自然的过分增强。
(4)应用:改善光线对图像处理的影响。成像中由于光照过大或过小,会造成图像结果偏暗或偏亮或者光线不均匀,这样图像直方图就会表现:灰度的两个高峰分别向某一边滑动,同时灰度值都较为集中,不能真实反应目标图像的特征。所以使用直方图均衡化可以减少这种影响。
(5)直方图均衡化步骤:
①找到一个映射函数,定义为g = EQ (f)。f完整表示是f(x,y),代表图像中某个位置的像素值;
②依次使用EQ将图像中每个位置的像素值映射为新的像素值。
4、直方图匹配(或直方图规定化)
答:直方图匹配是指将一个图像的直方图变换到指定的形状(直方图均衡化是变换到均匀分布),是一种图像增强技术;
5、直方图局部增强
答:前述直方图处理都是直接对整幅图像求直方图,然后针对直方图处理。而直方图局部增强则是对图像的每个指定大小区域分别求直方图,然后针对每个直方图进行均衡化或者规定化处理。
例如,用一个k*k的矩阵从图像左上角滑动,每滑动一次计算一次该矩阵范围内图像的直方图,进行相关直方图处理。直到整幅图都被滑过,就实现了局部增强操作。
作用:可以实现对图像细节的增强。
6、算术/逻辑操作增强
答:主要包括与、或、加、减法操作。
图像相减法:应用最为成功的是医学领域的掩模式X射线成像术,另外图像相减法在图像分割中也有应用;
7、空间滤波基础概念
答:(1)掩模:在滤波器中常提到的k*k的矩阵(一般k为奇数),用于依次滑过每一像素点并在每点进行滤波计算,矩阵中的数据成为掩模系数。
滤波器在每个像素点的滤波结果就是掩模与掩模覆盖下的图像进行计算得到的结果;如线性滤波器就是掩模系数与覆盖下的对应图像像素点进行乘法操作,最后求和得到的结果。
(2)邻域处理:上述线性滤波器就属于邻域处理滤波器,因为其将本像素点为中心的邻域像素都纳入计算中了;实际非线性滤波器也是邻域处理方式,如常见的非线性滤波器:中值滤波器。
(3)如何解决图像边缘掩模滤波问题:掩模移动都是以矩阵中心作为基准点的,那么对于图像边缘,掩模矩阵就会有一部分超出图像范围。一般解决方法有:
1)限制掩模移动范围,使得掩模始终在图像范围内。缺点是边缘部分像素得不到滤波处理;
2)使用灰度值0或者边缘灰度值扩充边缘,滤波后删除。缺点是影响靠近边缘像素的滤波结果;
3)掩模超出部分不参与滤波计算;
三种方式中1)是最佳选择。
8、平滑线性滤波器
答:常见的线性滤波器有:均值、加权均值滤波器等。
以掩模为3*3为例:
1/9*
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
1/16*
| 1 | 2 | 1 |
| 2 | 4 | 2 |
| 1 | 2 | 1 |
上述两个掩模构成的滤波器都可称为平滑线性滤波器,前者是最简单的均值滤波,后者是加权均值滤波。每个像素点的滤波结果就是掩模矩阵中心在该点时的掩模系数与下面相应像素灰度值的乘积求和。
其实对于不同掩模系数组合,掩模大小更能影响滤波结果。不同大小的掩模矩阵对于不同大小的噪声点会有不同的滤波效果。
9、统计排序滤波器
答:统计排序滤波器属于非线性滤波器,最常见的是中值滤波器;例如在一个3*3的矩阵范围内统计像素值并排序,取中值作为矩阵中心像素的灰度值。
10、椒盐噪声如何滤波?
答:椒盐噪声:也称为脉冲噪声:在图像中,它是一种随机出现的白点或者黑点,可能是亮的区域有黑色像素或是在暗的区域有白色像素(或是两者皆有)。
滤波方式:滤除椒盐噪声比较有效的方法是对信号进行中值滤波处理。顾名思义,中值滤波是指将一个像素的值用该像素邻域中强度值的中间值来取代,至于领域范围取多大则视实际需要而定。去除椒盐噪声的后可以得到较为平滑的信号,其效果要优于均值滤波器,当然同样也会造成边缘模糊、信号不够锐利,这似乎也是很多滤波方法的一大通病。
11、锐化空间滤波器
答:平滑通过均值实现(均值类似于积分),那么同理锐化就可以通过微分实现。常见的微分实现锐化有:一阶微分(梯度法)、二阶微分(拉普拉斯算子法)。
(1)常见的拉普拉斯锐化的最终掩模矩阵有如下4邻域和8邻域:
4邻域:
| 0 | -1 | 0 |
| -1 | 5 | -1 |
| 0 | -1 | 0 |
8邻域:
| -1 | -1 | -1 |
| -1 | 9 | -1 |
| -1 | -1 | -1 |
根据上述掩模矩阵就可以看出,经过掩模矩阵与覆盖像素的乘积求和后,可以增强某些灰度突变幅度,因此可以实现锐化。
作用:拉普拉斯锐化对于细节增强效果较好,如月球表面成像细节;
(2)梯度法实现锐化的掩模矩阵是一个组合,有两个组成(以3*3为例):
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| -1 | 0 | 1 |
注意:梯度法的掩模矩阵要保证所有掩模系数之和为0;
计算公式为:df=abs((z7+2*z8+z9)-(z1+2*z2+z3))+abs((z3+2*z6+z9)-(z1+2*z4+z7))
最终该像素点的锐化值=f(该点像素值)+df;
作用:梯度锐化法对于轮廓边缘增强效果较好,如工业缺陷轮廓检测。
注:梯度处理又称为Sobel处理。
12、滤波器分类
答:分为:空间滤波器与频域滤波器,分别对应空间域和频域中的滤波。
空间域滤波器就是直接针对图像矩阵本身的,有均值、中值、最大、最小滤波器等。前面所说的都是空间域内的滤波;
频域滤波器实际是将空间域信号转化到频域而成的,这样可以将一些干扰频率段的信号滤掉,实现增强效果。下面部分就准备介绍频域空间滤波;
13、频域信号与频域滤波的物理意义
答:(1)频域信号的物理意义:低频信号的大小主要表示图像的总体灰度级;高频信号主要表示图像的细节部分,如边缘和噪声;这样,在频域内可以容易的实现对高频噪声的滤除或者对低频灰度级的衰减以增强图像;
(2)频域滤波步骤:输入图像->前处理->傅里叶变换为频域信号->频域滤波函数进行滤波->傅里叶反变换转化为空间域信号->后处理->结果图像;
(3)频率滤波器主要分为低通滤波器和高通滤波器。低通会衰减高频信号,故起到平滑作用;高通会衰减低频信号,故起到锐化作用;
(3)频域滤波的意义:有很多情况下,空间域无法实现的滤波要求可以在频域轻松实现,所以频域滤波的作用常常是先用频域信号实现滤波器,然后再进行傅里叶反变换为空间域滤波器。起到一个中间作用,最终还是生成了空间域滤波器。
14、卷积定理在滤波中的应用
答:卷积原理:两个函数卷积的傅里叶变换=函数傅里叶变换后的乘积;
所以空间域中基于卷积运算的滤波器可以直接通过:先得到傅里叶变换后的频域函数乘积,然后对乘积结果求逆傅里叶变换即可,计算速度快,容易实
现。
可以说,卷积定理是空间域滤波和频域滤波之间的纽带。
15、频域低通滤波器和频域高通滤波器
答:频率域中,低通滤波器和高通滤波器的生成实际就是创建合理的频率域滤波函数曲线;
(1)频域低通滤波器有:频域理想低通滤波器、频域巴特沃斯低通滤波器、频域高斯低通滤波器等;
理想低通滤波器的函数曲线是类似脉冲函数,低频和高频间过渡十分剧烈,是无法实现的;
巴特沃斯低通滤波器和高斯低通滤波器的函数曲线在低频和高频处过渡较为平缓,可以实现。其中高斯低通滤波器应用较为常见,其主要用于平滑图像,减少边缘毛刺、消除轮廓缺断等作用。
(2)频域高通滤波器的滤波函数曲线的纵轴方向取值与低通滤波曲线相反,主要集中在横轴的高频部分,所以对于低频有抑制作用。
频域内的高通滤波器有:频域理想高通滤波器、频域巴特沃斯高通滤波器、频域高斯高通滤波器、频域拉普拉斯滤波器;
频域高通滤波器还有很多改进型,如高斯高通滤波器的改型有:高斯高通加强型滤波器、同态滤波器等。
16、Gabor滤波器原理
答:原理:Gabor变换在前面章已经讲过了,就是短时傅里叶变换。正是基于Gabor变换具有时频结合特性,可以同时在时间域和频率域获取局部
信息,从而使得Gabor 滤波器具有在空间域和频率域同时取得最优局部化的特性,因此能够很好地描述对应于空间频率(尺度)、空间位置及方向选择性
的局部结构信息,从而实现局部高质量滤波;
Gabor滤波器时间窗口选择:根据信号频率确定,频率越高,时间窗口越小;
Gabor滤波器的频率和方向表示接近人类视觉系统对于频率和方向的表示,并且它们常备用于纹理表示和描述。在图像处理领域,Gabor滤波器是一个
用于边缘检测的线性滤波器。
第三章、图像复原
1、什么是图像复原?
答:图像复原:主要是使用一个复原函数对退化的图像进行最大限度的复原(需要知道一些关于输入图像的退化函数以及噪声函数知识,才可以生成复原函数)。主要包括空间噪声滤波、线性与非线性滤波等各种滤波,以及图像几何变换与图像配准等操作;
2、复原模型
答:(1)退化模型函数g=f*h+n;
即:输入图像f被退化函数h进行了卷积运算,然后又加上噪声函数n的干扰,就是我们采集输出的图像g;
要复原图像就要进行反操作:减去噪声函数n,然后进行卷积逆变换。
复原模型的生成步骤:预估噪声模型和退化函数->逆操作->复原图像;
(2)噪声模型估计:
噪声模型的选择需要根据图像的傅里叶频谱情况进行估计。
常见的噪声模型包括:高斯噪声、瑞利噪声、伽马噪声、指数噪声、均匀噪声和脉冲噪声等。估计时根据情况选择前面所述近似的模型即可。
当退化模型中只存在噪声模型时,图像复原就和图像增强没有区别了,即只需要消除噪声就可,此时可直接进行空间滤波即可。如:均值滤波(算术均值、几何均值、谐波均值逆谐波均值滤波)、统计排序滤波(中值、最大最小值、中点、修正阿尔法滤波)、自适应滤波。
(3)退化函数估计:
退化函数估计方法有:观察法、试验法、数学建模法。
(4)常见的复原方法和模型有:
逆滤波器、最小均方误差滤波(维纳滤波)器、约束最小二乘方滤波器、几何均值滤波器(最广义化的复原模型);
3、图像倾斜校正
答:倾斜校正对于图像处理,尤其是文本识别、车牌识别等都是必要的图像复原步骤。主要的倾斜校正方法有哈夫变换法、投影法、近邻法等,其中哈夫变换是最经典的,投影法是最常用的。
以车牌矫正或文本识别为例:车牌字符要实现良好分割,就需要保证车牌是水平的,所以车牌矫正必不可少。
1)哈夫变换法:对矩形车牌进行边缘提取,然后对矩形长边缘进行哈夫直线检测,根据检测到的最长直线首尾坐标可以求得斜率,从而就可获知车牌倾斜度;
2)radon变换(或叫拉东变换):就是投影法,原理:对倾斜目标的图像在不同的倾斜角度(0:179°)范围内进行投影,然后查找使投影结果具有最大峰值的那个投影角度。记录这一角度,就是倾斜的角度。
拉东变换原理:如下图,白色方块代表图片目标,箭头代表投影方向,坐标轴x始终与投影方向垂直,坐标上的投影曲线是每条射线方向像素点灰度的累加和。由图可知,只有顺着长方形图像目标长边方向的投影才可以得到最大峰值,因此该投影方向可以看做方块的方向角。
车牌或文字方向校正,都可以参考这种方法。
3)K-最近邻法(KNN):先找出目标区域内所有的连通区域(文本识别中每一个连通区就是一个字符),然后将所有连通区中K个最邻近的连通区中心点两两相连成矢量,计算矢量方向角度并绘制直方图,直方图的峰值就是目标区域倾斜角度。
第四章、彩色图像处理
1、常用有颜色空间RGB,YUV,HSI,HSV
答:①RGB颜色空间:
该颜色空间主要用于计算机图形学中,它是指图像中每一个像素都具有R,G,B三个颜色分量,这三个分量大小均为[0,255],以这三个分量为坐标轴,构建一个三维颜色空间,这样,颜色空间中每一个三维坐标都将表示一种颜色。但RGB并不能表示所有颜色;
RGB图像的每个像素有三个分量组成,所以可以看作是一个向量,而不是一个点。
②HSI颜色空间:
HSI颜色空间是从人的视觉系统出发,用色调(Hue)、色饱和度(Saturation)、亮度 (Intensity)来描述色彩(HSI就是三者简写组合)。
HSI色彩空间可以用一个圆锥空间模型来描述,这种色彩空圆锥模型相当复杂,但确能把色调、亮度和色饱和度的变化情形表现得很清楚;
HSI最大的好处就是可以颜色空间分为彩色和灰度信息,这样就可以利用彩色特征进行图像处理,例如车牌识别中常根据车牌的色彩信息进行定位车牌。
③YUV颜色空间:
该颜色空间是PAL制式和SECAM制式采用的颜色空间,其中Y代表亮度,UV代表色度。“亮度”是通过RGB输入信号来建立的,方法是
将RGB信号的特定部分叠加到一起。“色度”则定义了颜色的两个方面,色调(hue)与饱和度(saturation)。
2、彩色模型间的转换
答:数字图像处理中最常见的转换为:RGB->HSI与HSI->RGB;
3、伪彩色处理技术
答:(1)强度分层技术:将图像信息描述为一幅灰度三维图,用一个或多个平面切割灰度图,被切割的上下两部分用不同颜色表示,可以显示灰度图中不明显的信息。
实质是:将灰度图中不同灰度级赋予不同颜色,以便显现细节信息和区分不同特征。
应用:如焊缝的X光检测中,可以用强度分层技术来判断焊接质量;医学生的甲状腺加强显示技术;卫星云图中用分层加强技术突出降雨水平等。
(2)灰度级到彩色图转换(实际上是伪彩色图)
实质:强度分层是最简单的灰度图转化为伪彩色图技术,而灰度级到彩色转换是使用正弦变换函数分别实现灰度到R、G、B三色的转换,最终合成彩色图像。
应用:机场和车站的X光扫描机拍的图片就需要经过灰度级到彩色图的转换,以显现危险物品;如今的一些彩色红外夜视仪也是经过灰度级到彩色图转换技术实现的彩色显示;
3、全彩色图像处理(不涉及邻域像素)
答:(1)补色:补色类似于灰度反转,即将一种色调转换到色环上与其对立的另一种色调。
作用:不舍对于增强嵌在彩色图像暗区的细节,特别是在大小上占支配地位的细节很有用。
(2)彩色分层
(3)色调与彩色校正
(4)彩色图像的直方图均衡化:在HSI空间对亮度进行均衡改变,而不改变色调和饱和度。该法只适合HSI空间。
4、平滑与尖锐化
答:上述彩色图像处理中主要是针对单个像素进行处理,这里则是在邻域基础上进行处理。
(1)彩色图像平滑滤波:同样使用灰度图平滑方法,对于RGB空间每个颜色分量分别使用灰度图平滑滤波的方式进行平滑处理,然后就将处理后的图片分量合在一起;对于HSI空间,一般平滑操作只针对亮度I分量即可。
(2)彩色锐化处理:同样适用灰度图锐化方法,对于RGB空间每个颜色分量进行锐化处理,然后将处理后的结果合成;对于HSI空间,一般只对亮度I分量进行锐化操作;
5、彩色图像分割
答:一般使用HSI或者RGB空间作为彩色分割颜色空间。
HSI空间分割:将图像转化到HSI空间,一般针对饱和度分量图片进行操作;
RGB空间分割:根据目标区域的平均RGB向量,对图像进行相似度比较,比较方法为欧氏距离比较法。
彩色边缘检测:灰度图中使用梯度法进行边缘检测(Sobel算子),但像素是一个点,在彩色图中像素是一个向量,所以可以将梯度法拓展到向量领域。
第五章、图像压缩
1、图像金字塔
答:就是以源图为基座,每向上一层就将分辨率的长宽降低0.5倍。如一幅图为512*512的分辨率,作为基座J级。那么上面一级J-1级的图像就是将原图分辨率变为256*256的的图片。J-2级就是分辨率变为128*128的,……
至于缩小分辨率如何实现:以步长2进行抽样,就可以实现降分辨率;
2、残差金字塔
答:残差金字塔用于表示图像重建后与源图的差异,实际常用于图像重建中;
残差金字塔形成:对每一级降分辨率图像进行步长为2的重建(即以像素拓展形式扩大分辨率),将本级的下面邻级与本级重建后的图像进行做差,得到的就是残差金字塔中对应级别的图像。
解释:图像金字塔常用于图像压缩;残差金字塔常用于图像还原;
3、快速傅里叶变换(FFT)与小波变换
答:定义:FFT是离散傅里叶变换(DFT)的一种快速算法,其时间复杂度由原来DFT的O(n^2)减少到O(nlogn);
作用:将时域离散信号变换到频域信号;
一维连续时域信号经过FFT的示例如下图:
坐标解释:频谱坐标系的x,y坐标轴物理意义:x是频率,y是该频率的幅度(即处于该频率的信号强度);
①可见,做完FFT后可以在频谱上看到清晰的四条线,即信号包含四个频率成分。上述频谱图中各频率信号的幅值(信号强度)基本
相等,也就是平稳的频域信号,所以只需要知道信号频率分布情况即可;
②然而对于非平稳的频域信号(各个幅值不等),仅仅知道频率分布是不够的,还需要知道某个时间的信号频率情况,因此提出了:
短时傅里叶变换(简称SIFT,注意不是SIFT特征检测算子),短时傅里叶变换也可以叫做Gabor变换(因为由gabor提出);
SIFT即“把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么
频率了”,这就是短时傅里叶变换。
③SIFT实现了频域信息和时域信息的同时获取,但SIFT有一个缺陷——一个信号序列的时间分割窗口宽度都一样,这样会造成一些
问题:窄窗口时间分辨率高、频率分辨率低,宽窗口时间分辨率低、频率分辨率高。对于时变的非稳态信号,高频适合小窗口,低
频适合大窗口。然而STFT的窗口是固定的,在一次STFT中宽度不会变化,所以STFT还是无法满足非稳态信号变化的频率的需
求。
④对于SIFT的固定窗口问题,就可以引入“小波变换”。
小波变换:小波直接把傅里叶变换的基给换了,即“将无限长的三角函数基换成了有限长的会衰减的小波基”,这样不仅能够获取完整
的频率信息,还可以得到更高的时间分辨率,从而实现知道每个时刻的信号频率信息。
4、傅里叶分析与小波分析的区别
答:小波变换与傅里叶变换不同,小波变换基于一些小型正交波(傅里叶变换基于正弦函数),所以称为小波。小波具有变化的频率和有限的持续时间。
(1)有人用两句话概括:
傅里叶变换:知道一段时间内,信号的各个频率分量分别是多少;
小波变换:知道一段时间内,信号的各个频率分量分别是多少,以及它们是在什么时候出现的;
也就是说“傅里叶变换后丢失了时间域信息,而小波变换则是实现了时频结合”;
(2)用一个形象的说法解释:
以一首歌做比方,傅立叶变换可以告诉你这首歌高、中、低音所占的能量是多少以及它们具体的平均频率;小波分析不仅能做
到这一点,还可以告诉你这首歌具体某一时刻高中低频分量的分布情况。
5、小波变换与图像压缩应用
答:(1)上述图像金字塔和残差金字塔实质就是多分辨率处理的内容。多分辨率常用于图像压缩,小波变换最大的用处也是图像压缩;
图像的小波压缩过程首先是对原始图像进行二维小波变换,得到小波变换系数。由于小波变换能将原始图像的能量集中到少部分小波系数上,且分解后的小波系数在三个方向的细节分量有高度的局部相关性,为进一步量化编码提供了条件,因此小波编码可以获得较高的压缩比,且压缩速度较快。
小波压缩的特点在于压缩比高,压缩速度快,压缩后能保持信号与图像特征基本不变,并且传输过程中可以抗干扰。
(2)一维小波变换
小波变换的基本思想是用一组小波或基函数表示一个函数或信号,例如图像信号。以哈尔(Haar)小波基函数为例,基本哈尔小波函数(Haar wavelet function)定义如下:
1, 当0≤x<1/2
Ψ(x) = { -1, 当1/2≤x<1
0, 其他
设有一幅分辨率只有4个像素的一维图像,对应像素值为:[9 7 3 5]。用哈尔小波变换的过程是:计算相邻像素对的平均值(averaging,亦可称之为近似值approximation),得到一幅分辨率为原图像1/2的新图像:[8 4]。这时图像信息已部分丢失,为了能从2个像素组成的图像重构出4个像素的原图像,必须把每个像素对的第一个像素值减这个像素的平均值作为图像的细节系数(detail coefficient)保存。因此,原图像可用下面的两个平均值和两个细节系数表示:[8 4 1 -1]。可以把第一步变换得到的图像进一步变换,原图像两级变换的过程如表1所示:
(3)二维小波变换
介绍一下二维小波变换的塔式结构。我们知道,一维小波变换其实是将一维原始信号分别经过低通滤波和高通滤波以及二元下抽样得到信号的低频部分L和高频部分H。而根据Mallat算法,二维小波变换可以用一系列的一维小波变换得到。对一幅m行n列的图像,二维小波变换的过程是先对图像的每一行做一维小波变换,得到L和H两个对半部分;然后对得到的LH图像(仍是m行n列)的每一列做一维小波变换。这样经过一级小波变换后的图像就可以分为LL,HL,LH,HH四个部分,如下图所示,就是一级二维小波变换的塔式结构:
而二级、三级以至更高级的二维小波变换则是对上一级小波变换后图像的左上角部分(LL部分)再进行一级二维小波变换,是一个递归过程。下图是三级二维小波变换的塔式结构图:
一个图像经过小波分解后,可以得到一系列不同分辨率的子图像,不同分辨率的子图像对应的频率也不同。高分辨率(即高频)子图像上大部分点的数值都接近于0,分辨率越高,这种现象越明显。要注意的是,在N级二维小波分解中,分解级别越高的子图像,频率越低。例如图2的三级塔式结构中,子图像HL2、LH2、HH2的频率要比子图像HL1、LH1、HH1的频率低,相应地分辨率也较低。根据不同分辨率下小波变换系数的这种层次模型,我们可以得到以下三种简单的图像压缩方案。
方案一:舍高频,取低频
一幅图像最主要的表现部分是低频部分,因此我们可以在小波重构时,只保留小波分解得到的低频部分,而高频部分系数作置0处理。这种方法得到的图像能量损失大,图像模糊,很少采用。
另外,也可以对高频部分的局部区域系数置0,这样重构的图像就会有局部模糊、其余清晰的效果。
方案二:阈值法
对图像进行多级小波分解后,保留低频系数不变,然后选取一个全局阈值来处理各级高频系数;或者不同级别的高频系数用不同的阈值处理。绝对值低于阈值的高频系数置0,否则保留。用保留的非零小波系数进行重构。Matlab中用函数ddencmp()可获取压缩过程中的默认阈值,用函数wdencmp()能对一维、二维信号进行小波压缩。
方案三:截取法
将小波分解得到的全部频率系数按照绝对值大小排序,只保留最大的x %的系数,剩余的系数置0。不过这种方法的压缩比并不一定高。因为对于保留的系数,其位置信息也要和系数值一起保存下来,才能重构图像。并且,和原图像的像素值相比,小波系数的变化范围更大,因而也需要更多的空间来保存。
6、小波压缩的优点
答:(1)经过小波分解后的图像矩阵的局部统计数据稳定且易给出模型;
(2)其大多数值都接近0,对于图像压缩非常有利;
7、图像压缩分类
答:分为无损压缩和有损压缩;
无损压缩:(1)最简单的实现就是减少仅有的编码冗余,及通过对灰度表示的编码进行调整,以减少不必要的编码位,如变长编码(霍夫曼编码、算术编码);
(2)减少像素间冗余也是无损压缩的实现方式,如LZW编码、位平面编码;
(3)通过直接对像素进行操作实现消除较为接近的像素,该方法称为无损预测编码;
有损压缩:(1)有损预测压缩(直接对像素进行操作);
(2)变换编码(对编码方式进行操作);
(3)小波编码;
8、图像压缩标准
答:(1)静止图像压缩标准:
①JPEG:默认是霍夫曼编码,用于连续色凋、多级灰度、彩色/单色静态图像压缩,为有损模式。但完整的JPEG包括3套编码系统,分别是有损基本编码、拓展编码、可逆压缩的无损编码;
②JPEG2000:该压缩标准相对JPEG拥有更大灵活性,但未被采用;
(2)动态图像压缩标准:
MPEG是运动图像专家组的简称,其制定的动态图像压缩标准称为MPEG标准,包括MPEG-1、MPEG-2、MPEG-4、MPEG-7和MPEG-21;
9、图像信息量和图像熵的计算
答:(1)图像灰度级数=最大灰度值+1,如最大灰度值255的灰度图,灰度级数为256;
(2)图像中信息量=log2(灰度范围)
如:[0~255]的灰度图的信息量就等于log2(256)=8;
意义:信息量用于表示当前信息中的有效信息多少;
(3)图像熵:
熵: 熵是信息论中对不确定性的度量,是对数据中所包含信息量大小的度量;
图像的一维熵可以表示图像灰度分布的聚集特征,却不能反映图像灰度分布的空间特征;
为了表征这种空间特征,可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量就组成图像的二维熵。
第六章、形态学处理
1、膨胀与腐蚀
答:膨胀:主要将二值化图中断开的图像轮廓边缘连接起来,或将边缘缺口、内部孔洞等填充,效果好于平滑滤波;
腐蚀:主要将取出二值化图 进行收缩,去除不必要的细节,或细化轮廓。腐蚀对于去除小颗粒以及消除目标物之间的粘连是非常有效的 ;
结构元素:由数值为1或0组成的矩阵,在每个像素位置与二值图像对应的区域进行特定的逻辑运算。运算结果为输出图像相应的像素。运算效果取决于结构元素的大
小内容以及逻辑运算的性质。结构元素一般有以下几种类型:水平、垂直、十字、方形、其他。

腐蚀与膨胀原理介绍(以前景是白色1,背景色是黑色0为例进行介绍):
①、腐蚀原理:使用一个nXn结构元素如全为1的方形结构元素,去扫描图像中的每一个像素。用结构元素与其覆盖的原二值图像做“与”操作,如果原结构元素中1对应位置的逻辑运算结果都为1,这图像的该像素为1,否则为0。简言之就是腐蚀是选择结构元素范围内的最小值。腐蚀之后,图像边界向内收缩;
②、膨胀原理:使用一个nXn结构元素如全为1的方形结构元素,去扫描图像中的每一个像素。用结构元素与其覆盖的原二值图像做“与”操作,如果原结构元素中1对应位置的逻辑运算都为0,这图像的该像素为0,否则为1。简言之就是腐蚀是选择结构元素范围内的最大值。膨胀之后,图像边界向外扩大;
实际上,应用中腐蚀就是细化白色前景,膨胀就是扩张白色前景,即主要针对白色前景黑色背景的。所以,要是前景是黑色,可以交换腐蚀和膨胀使用或者对图像进行反变换再使用。
2、开运算与闭运算
答:开运算:先腐蚀后膨胀;
闭运算:先膨胀后腐蚀;
作用:都有平滑作用,可以滤除噪声,只是开运算在平滑后会造成部分较细轮廓断,闭运算在平滑后会使得轮廓边缘加强;
补充:一般除了二值图的开闭运算,还有灰度图开闭元算。原理一致:就是提取结构元范围内的最小灰度值或最大灰度值(二值图也是提取最小最大值0或者1),就是将二值拓展到灰度范围。
3、击中或击不中变换
答:定义:首先对用s1对目标图像X进行腐蚀得到A1, 用s2对Y(即~X,目标图像X的补)进行腐蚀得到A2。最终结果C = A1 & A2。
作用:形态学的击中和击不中是一种匹配技术,是形状检测的基本工具,。实际上变换后容易产生噪声,实用意义不大。
4、形态学算法应用
答:(1)提取边缘:①β(A)=A-(用B腐蚀A的结果):充分利用腐蚀技术,提取物体轮廓;②膨胀-源图;③膨胀-腐蚀;④膨胀-闭运算;⑤开运算-腐蚀;
⑥开运算膨胀-闭运算腐蚀;⑦闭运算开运算-闭运算腐蚀;⑧多结构元边缘检测;
具体的,④⑤⑥⑦⑧都具有抗噪声能力,其中⑧的边缘提取效果最好,抗噪能力也最佳。⑧有如下3中类型的边缘提取方式:
性能:基于形态学的边缘检测在前人实验中表明其提取效果好于传统方案如Sobel算法等,抗噪声能力强。
(2)孔洞填充:X=(用B腐蚀A)∩A的补。迭代结束后X即为所求;
利用膨胀技术,将目标区域内部的干扰色块去除,填充成目标区域同样的颜色。利用A的补相交限制膨胀范围;
(3)提取连通分量区域:X=(用B腐蚀A)∩A。迭代结束后X即为所求;
有时根据情况,需要在迭代寻找连通域前,进行腐蚀操作,以去掉部分由于噪声干扰产生的连通域;
(4)凸壳:是为了找到一个凹陷的物体外壳,以不完美命中(腐蚀)为主要操作,通过调整结构元,加上原图,得到相关凸起结果;
(5)细化:图像细化一般作为一种图像预处理技术出现,目的是提取源图像的骨架,即是将原图像中线条宽度大于1个像素的线条细化成只有一个像素宽,形成“骨架”,形成骨架后能比较容易的分析图像,如提取图像的特征。
细化基本思想是“层层剥夺”,即从线条边缘开始一层一层向里剥夺,直到线条剩下一个像素的为止。
(6)骨架:使用形态学腐蚀减去结果的开运算的骨架与细化相比,缺少的就是同伦性(同伦性:连通域结构保持不变的特性),即骨架操作得到的并不是原图像的同伦变换,而且这种骨架有些地方并不是一个像素,而是多个像素。
(7)顶帽(top Hat):顶帽就是原图与开运算图之差;结果图突出了比原图轮廓周围的区域更明亮的区域,且这一操作与选择的核的大小有关。顶帽运算往往用来分离比邻近点亮一些的斑块,在一幅图像具有大幅的背景,而微小物品比较有规律的情况下,可以使用顶帽运算进行背景提取。
(8)黑帽(black Hat):黑帽就是原图与闭运算图之差;黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域,且这一操作与核的大小有关。黑帽运算用来分离比临近点暗一点的斑块,效果图有着非常完美的轮廓。
(9)裁剪:相对骨架而言的,有些骨架操作结果会产生毛刺,即突出的像素,就需要裁剪;
(10)形态学滤波:开-闭滤波、闭-开滤波、复合形态学滤波;
更多具体:http://blog.csdn.net/zizi7/article/details/50896545(1)
http://blog.csdn.net/zizi7/article/details/50907949(2)
部分操作的C++实现代码:http://blog.csdn.net/tonyshengtan/article/details/42263347
注意:上述形态学处理都是在二值化图中进行,虽然形态学处理可以拓展到灰度级图,但应用方向有所改变;
第七章 图像分割
1、间断检测
答:(1)点检测:孤立点检测一般使用一个3*3的模板,进行乘积之和的判断。模板矩阵如下:
| -1 | -1 | -1 |
| -1 | 8 | -1 |
| -1 | -1 | -1 |
设定一个门限值T,判断:
R的绝对值>=T是否成立;
若成立矩阵中心下的像素点就是孤立点,否则不是孤立点;
这中孤立点检测可以应用到孤立噪声滤波、或故障检测(航空发动机叶片表面通风孔检测)等方面;
(2)线检测:使用3*3矩阵对图像进行滑动计算乘积之和计算,并将结果与门限值T进行比较判断。
模板矩证如下:包括4个方向的线检测模板矩阵,分别是水平、正45度、垂直、负45度。
| -1 | -1 | -1 |
| 2 | 2 | 2 |
| -1 | -1 | -1 |
| -1 | -1 | 2 |
| -1 | 2 | -1 |
| 2 | -1 | -1 |
| -1 | 2 | -1 |
| -1 | 2 | -1 |
| -1 | 2 | -1 |
| 2 | -1 | -1 |
| -1 | 2 | -1 |
| -1 | -1 | 2 |
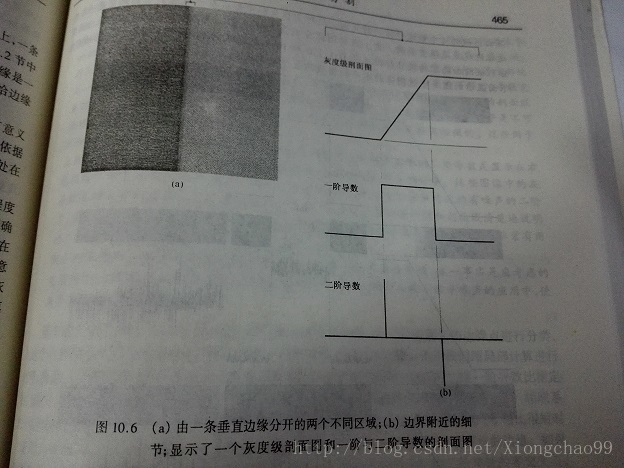
(3)边缘检测
图像边缘一般是在前景和背景交界处,理想的边缘处灰度会发生突变。但实际上,边缘的灰度都是线性变化的,即有一段宽度的灰度变化带。常用的边缘提取方法有:一阶导数(梯度法)和二阶导数(拉普拉斯算子);
前者可以直接求出边缘灰度变化的斜率,后者可以求出两个突变点的斜率变化速度。如下图所示:
(一)梯度法检测:
对于图像边缘区域的像素矩阵:
梯度法边缘检测模板有如下几种:
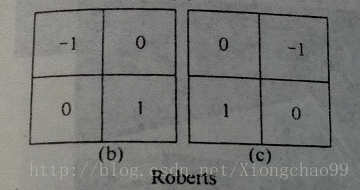
①Roberts模板
模板为2*2矩阵,是最简单的梯度法边缘检测模板;
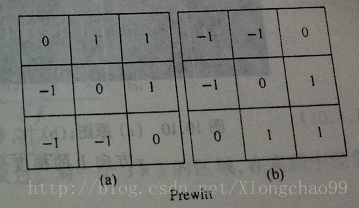
②Prewitt模板
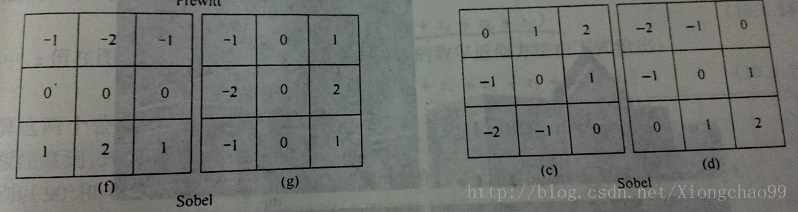
分别是水平垂直方向检测模板与斜正负45度方向检测模板:

可见,相比Roberts模板变为3*3,具有中心点了;
③Sobel模板
分别是水平垂直方向检测模板与斜正负45度方向检测模板:
可见,相比Prewitt模板,Sobel模板使用了一个权值2,来加强中心点,以实现平滑灰度区域,抑制噪声。
梯度计算结果就是上述水平垂直两个模板矩阵(或者正负斜45度两矩阵)与覆盖下的像素矩阵求乘积之和,然后将两个模板阵的乘积之和的绝对值相加即是梯度。
如Sobel求梯度:
▽f就是梯度值,根据梯度值就可以确定灰度值变化区域,进而找到边缘变化区域;
(二)拉普拉斯检测(二阶导数):
四邻域和八邻域的模板如下:
| 0 | -1 | 0 |
| -1 | 4 | -1 |
| 0 | -1 | 0 |
| -1 | -1 | -1 |
| -1 | 8 | -1 |
| -1 | -1 | -1 |
注意:拉普拉斯算子一般不会直接用于边缘检测,因为作为二阶导数,对噪声敏感且容易产生双边缘,同时不能检测边缘方向。
一般拉普拉斯算子用于:(1)利用零交叉性质进行边缘定位;(2)确定一个像素是在边缘亮的一边还是暗的一边;
使用零交叉进行边缘定位识别得到的边缘比较细,但具有空心粉效应以及计算量大等缺陷,所以应用不多。
总结:梯度法求边缘的应用最为广泛。
2、常用边缘检测有哪些算子,各有什么特性?
答:常用边缘检测算子如下所述:
(1)Roberts算子
罗伯茨算子、Roberts算子是一种最简单的算子,是一种利用局部差分算子寻找边缘的算子,他采用对角线方向相邻两象素之差近似梯度幅值检测边缘。检测垂直边缘的效果好于斜向边缘,定位精度高,对噪声敏感,无法抑制噪声的影响。1963年,Roberts提出了这种寻找边缘的算子。Roberts边缘算子是一个2x2的模板,采用的是对角方向相邻的两个像素之差。从图像处理的实际效果来看,边缘定位较准,对噪声敏感。适用于边缘明显且噪声较少的图像分割。Roberts边缘检测算子是一种利用局部差分算子寻找边缘的算子,Robert算子图像处理后结果边缘不是很平滑。经分析,由于Robert算子通常会在图像边缘附近的区域内产生较宽的响应,故采用上述算子检测的边缘图像常需做细化处理,边缘定位的精度不是很高。
(2)Prewitt算子
Prewitt算子是一种一阶微分算子的边缘检测,利用像素点上下、左右邻点的灰度差,在边缘处达到极值检测边缘,去掉部分伪边缘,对噪声具有平滑作用 。其原理是在图像空间利用两个方向模板与图像进行邻域卷积来完成的,这两个方向模板一个检测水平边缘,一个检测垂直边缘。经典Prewitt算子认为:凡灰度新值大于或等于阈值的像素点都是边缘点。即选择适当的阈值T,若P(i,j)≥T,则(i,j)为边缘点,P(i,j)为边缘图像。这种判定是欠合理的,会造成边缘点的误判,因为许多噪声点的灰度值也很大,而且对于幅值较小的边缘点,其边缘反而丢失了。Prewitt算子对噪声有抑制作用,抑制噪声的原理是通过像素平均,但是像素平均相当于对图像的低通滤波,所以Prewitt算子对边缘的定位不如Roberts算子。因为平均能减少或消除噪声,Prewitt梯度算子法就是先求平均,再求差分来求梯度。该算子与Sobel算子类似,只是权值有所变化,但两者实现起来功能还是有差距的,据经验得知Sobel要比Prewitt更能准确检测图像边缘
(3)Sobel算子(常用的单独边缘提取算法)
Sobel算子主要用于边缘检测,在技术上它是以离散型的差分算子,用来运算图像亮度函数的梯度的近似值,Sobel算子是典型的基于一阶微分的边缘检测算子,由于该算子中引入了类似局部平均的运算,因此对噪声具有平滑作用,能很好的消除噪声的影响。Sobel算子对于象素的位置的影响做了加权,与Prewitt算子、Roberts算子相比因此效果更好。Sobel算子包含两组3x3的矩阵,分别为横向及纵向模板,将之与图像作平面卷积,即可分别得出横向及纵向的亮度差分近似值。缺点是Sobel算子并没有将图像的主题与背景严格地区分开来,换言之就是Sobel算子并没有基于图像灰度进行处理,由于Sobel算子并没有严格地模拟人的视觉生理特征,所以提取的图像轮廓有时并不能令人满意。
(4)Laplacian算子
Laplace算子是一种各向同性算子,二阶微分算子,在只关心边缘的位置而不考虑其周围的象素灰度差值时比较合适。Laplace算子对孤立象素的响应要比对边缘或线的响应要更强烈,因此只适用于无噪声图象。存在噪声情况下,使用Laplacian算子检测边缘之前需要先进行低通滤波。所以,通常的分割算法都是把Laplacian算子和平滑算子结合起来生成一个新的模板。拉普拉斯算子也是最简单的各向同性微分算子,具有旋转不变性。一个二维图像函数的拉普拉斯变换是各向同性的二阶导数。拉式算子用来改善因扩散效应的模糊特别有效,因为它符合降制模型。扩散效应是成像过程中经常发生的现象。一般使用的是高斯型拉普拉斯算子(Laplacian of a Gaussian,LoG),在LoG公式中使用高斯函数的目的就是对图像进行平滑处理,使用Laplacian算子的目的是提供一幅用零交叉确定边缘位置的图像;图像的平滑处理减少了噪声的影响并且它的主要作用还是抵消由Laplacian算子的二阶导数引起的逐渐增加的噪声影响。
(5)Laplacian of Gaussian(LoG)算子 (高斯拉普拉斯边缘检测,又叫墨西哥草帽边缘检测)
利用图像强度二阶导数的零交叉点来求边缘点的算法对噪声十分敏感,所以,希望在边缘增强前滤除噪声.为此,将高斯滤波和拉普拉斯边缘检测结合在一起,形成LoG(Laplacian of Gaussian, LoG)算法,也称之为拉普拉斯高斯算法.LoG边缘检测器的基本特征是: 平滑滤波器是高斯滤波器.增强步骤采用二阶导数(二维拉普拉斯函数).边缘检测判据是二阶导数零交叉点并对应一阶导数的较大峰值.使用线性内插方法在子像素分辨率水平上估计边缘的位置.这种方法的特点是图像首先与高斯滤波器进行卷积,这一步既平滑了图像又降低了噪声,孤立的噪声点和较小的结构组织将被滤除.由于平滑会导致边缘的延展,因此边缘检测器只考虑那些具有局部梯度最大值的点为边缘点.这一点可以用二阶导数的零交叉点来实现.拉普拉斯函数用作二维二阶导数的近似,是因为它是一种无方向算子.为了避免检测出非显著边缘,应选择一阶导数大于某一阈值的零交叉点作为边缘点.
(6)Canny算子(常用的完整边缘提取算法)
Canny算子是一个具有滤波,增强,检测的多阶段的优化算子,在进行处理前,Canny算子先利用高斯平滑滤波器来平滑图像以除去噪声,然后采用一阶偏导的有限差分来计算梯度幅值和方向,接着Canny算子还将经过一个非极大值抑制的过程,最后Canny算子还采用两个阈值来连接边缘。
边缘提取的基本问题是解决增强边缘与抗噪能力间的矛盾,由于图像边缘和噪声在频率域中同是高频分量,简单的微分提取运算同样会增加图像中的噪声,所以一般在微分运算之前应采取适当的平滑滤波,减少噪声的影响。Canny运用一个准高斯函数作平滑运算,然后以带方向的一阶微分定位导数最大值,Canny算子边缘检测是一种比较实用的边缘检测算子,具有很好的边缘检测性能。Canny边缘检测法利用高斯函数的一阶微分,它能在噪声抑制和边缘检测之间取得较好的平衡。
3、hough变换
答:(1)原理:Hough变换的基本原理在于利用点-线的对偶性,将原始图像空间x-y中给定的曲线通过曲线表达形式变为参数空间的一个点。这样就把原始图像中给定曲线的检测问题转化为寻找参数空间中的峰值问题。也即把检测整体特性转化为检测局部特性。比如直线、椭圆、圆、弧线等。
(2)Hough变换检测直线的算法步骤:
①在ρ,θ的极值范围内对其分别进行m,n等分,设一个二维数组的下标与ρi,θj的取值对应;
②对图像上的边缘点作Hough变换,求每个点在θj变换后的ρi,判断(ρi,θj)与哪个数组元素对应,则让该数组元素值加1;
③比较数组元素值的大小,最大值所对应的 (ρi,θj)就是这些共线点对应的直线方程的参数。 共线方程为:ρi=x cosθj+y sinθj 。
(3)hough思路和拓展
具体参考:http://www.cnblogs.com/xfzhang/articles/1878561.html
4、二值化分割门限计算
答:(1)迭代法估计全局门限:
①选择一个T的初始值;
②用T分割图像。G1有所有的灰度值大于T的像素确定,G2由所有灰度值小于等于T的像素确定;
③对G1和G2区域像素分别求平均灰度值u1与u2;
④计算新的门限值T=1/2(u1+u2);
⑤重复②③④步骤,直至现在T相比上一个T的差小于某个值而止,现在的T就是所得到的门限值。
(2)基本自适应门限:
鉴于很多灰度图用一个全局门限无法实现二值化分割,因为光照不均匀而导致单一门限阈值不适用所有区域。所以可以将图像分割为多个子图像,然后分别采用迭代法求门限值。
注意:这里最重要的就是图像分割大小的确定,直接决定二值化分割效果;
5、基于区域分割
答:前面的图像分割分别是根据区域间的灰度不连续搜索边界、以及以像素性质分部为基础的门限分割。这里介绍直接寻找区域为基础的分割技术。
(1)区域生长法:先提取一组种子点(特征明显的目标区域),然后对每个像素根据特征公式计算特征集,然后根据相似性将种子点附近的相似像素纳入种子点所在区域,从而就可以实现区域生长;
(2)区域分离与合并;
6、基于形态学分水岭的分割
答:可以形象的解释:把灰度图的灰度值看做是地形不同高度,在每一个局部盆地的极小值表面,刺穿一个小孔,然后从该孔向盆地中灌入水,随着盆地中水灌入加多,相邻的两个集水盆汇合处构筑大坝,即形成分水岭。该分水岭就是我们分割中要找的分割边界。
分水岭分割实现:比较经典的分水岭计算分两个步骤,一个是排序过程,一个是淹没过程。首先对每个像素的灰度级进行从低到高排序,然后在从低到高实现淹没过程中,对每一个局部极小值在h阶高度的影响域采用先进先出(FIFO)结构进行判断及标注。分水岭变换得到的是输入图像的集水盆图像,集水盆之间的边界点,即为分水岭。显然,分水岭表示的是输入图像极大值点。因此,为得到图像的边缘信息,通常把梯度图像作为输入图。
分水岭分割的过度分割解决:为消除分水岭算法产生的过度分割,通常可以采用两种处理方法,一是利用先验知识去除无关边缘信息。二是修改梯度函数使得集水盆只响应想要探测的目标。
7、根据多幅图像分割出运动目标
答:有多幅图像,从中分隔出运动目标,一般采用多幅图像对比,找出位置移动的目标即为运动目标。
①寻找一副基准图像;
②获取每幅图像与基准图像的像素位置差异并记录;
③根据图像目标的累计差异获取每幅图像中的运动目标。
8、SIFT特征检测算子
答:SIFT,即尺度不变特征变换(Scale-invariant feature transform,SIFT),是用于图像处理领域的一种描述。具有缩放不变性和旋转不变性,对光照等自然干扰容忍度也很高,但该算法实时性不好。
SIFT算法用于特征匹配的过程:
①尺度空间极值检测:搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点;
②关键点定位:在每个候选的位置上,通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度;
③方向确定:基于图像局部的梯度方向,分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换,从而提供对于这些变换的不变性;
④关键点描述:在每个关键点周围的邻域内,在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种表示,这种表示允许比较大的局部形状的变形和光照变化;
⑤对测试图片和模板图的特征向量进行相似度匹配,进而对测试图中目标进行定位。
总结:SIFT是对测试图像和模板图进行关键点特征提取,然后获取特征向量,对两张图的特征向量使用欧氏距离公式进行相似性判断,最后将相似度高的特征点留下来用于目标定位。
SURF的过程与SIFT基本一致,只是其在SIFT基础上改进了一些算法,从而使得SURF实时性更佳,达到了SIFT的3倍处理速度。
第八章 图像描述
1、图像信息的表示方法
答:(1)链码:用于表示由顺序连接的具有指定长度和方向的直线段组成的边界线;
(2)多边形近似:分为最小周长多边形、聚合技术、拆分技术;
(3)标记图
(4)边界线段:即将边界分段,以减少边界复杂性
(5)骨架:前面在细化时已经提到过了。
2、边界描绘子
答:(1)简单边界描绘子:如边界长度、边界的直径与方向等;
(2)形状数
(3)傅里叶描绘子
(4)统计矩:如均值、方差和高阶矩,用于描述边界线段。
3、区域描绘子
答:(1)简单区域描绘子:如区域致密性(周长²/面积)、区域灰度均值\中值、最大灰度级值、最小灰度级值等;
(2)拓扑描绘子:主要是对图像平面的整体描述,如欧拉数=连通分量-孔的数,就是一个拓扑描述子;
(3)纹理:纹理描述3种主要方法是统计方法、结构化方法、和频谱方法。
①统计方法指平滑、粗糙、粒状等纹理特征的描述。具体有如:均值、标准差、统计矩、一致性参数、熵;
②结构化技术处理图像元的排列,如基于均匀空间分布的平行线纹理描述;
③频谱技术基于傅里叶频谱特性,主要用于通过识别频谱中高能量的窄波峰寻找图像中的整体周期性。
(4)图像不变矩:图像的不变矩可以由中心矩或者说是归一化中心矩构造而成,最著名Hu不变矩就是由二阶和三阶归一化中心矩构成,Hu矩具有平移、旋转和比例不变性。
①不变矩计算过程:
几何矩->中心矩->归一化中心矩->不变矩;
具体的不变矩公式自行百度谷歌即可。
②几何矩和不变矩的物理意义:
把二维灰度图看作一块薄板,每个点灰度值代表薄板在此处的质量密度。则几何矩意义可如下解释:
0阶几何矩表征薄板总质量(注意是表征,并不代表一定是);
1阶几何矩表征薄板质心位置;
2阶矩……
不变矩主要用于表征图像的形状特征,形状特征类似边长、周长、面积、圆周率、类圆率等。对于7个不变矩,它们是由各个表征形状单一特征的几何矩构造而成,所以并不能明确指出7个不变矩分别表征什么具体的物理特征。
③不变矩可以分为面不变矩和线不变矩:
面不变矩是指对给定图片的所有像素进行矩值运算;线不变矩则先提取目标边缘,然后对边缘进行矩运算。
由于目标形状主要由边缘确定,所以线矩对目标形状的表征和面矩性能差不多。但由于计算量大大减少,线矩计算具有更好的时间复杂度。
第九章 图像识别
1、基于决策理论方法的识别
答:使用决策理论进行识别是基于决策函数的识别。如对于多个模式类w1,w2,w3,w4....对应的判别函数分别是d1(x),d2(x),d3(x),d4(x),....,如果某个模式x属于类wi,则有
di(x)>dj(x) j=1,2,..., W; j≠i
模式类:一个模式类可以看做是具有相同特性的多个图像目标组成的一个集合;模式:模式就是模式类中的任一个元素;
2、基于决策理论识别——匹配
答:匹配:给定原型模式向量,将未知模式的向量与原型模式向量进行一定运算操作,根据运算结果来决策分类。
(1)最小距离分类器匹配:最简单的匹配方法,其运算操作就是计算原型模式与未知模式向量之间的欧氏距离,根据最小欧氏距离进行决策分类;
①根据给定的各种样本模式类,求取各个模式类的平均模式向量(最小距离分类器完全由每个类的平均向量确定);
②计算未知模式向量,计算其与各个样本平均模式向量之间的欧氏距离,未知模式就属于欧氏距离最小的样本模式类;
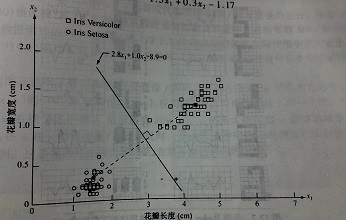
如何计算最小距离分类器中两个模式类的决策边界:
①根据计算两个模式类的平均模式向量;
②根据两个向量点计算两点之间的中垂分割线/面,即可;
决策判别函数如图:2.8x1+x2-8.9=0就是决策分解函数。
(2)相关性匹配(模板匹配):
给定一个M*N的图片和一个J*K的子图,使得子图在原图中滑动,每滑动一个像素子图就与其覆盖下的原图部分像素进行相关性运算,当滑动完成后所得的最大相关值对应的原图部分就是匹配目标;相关性计算的基本公式如下:
其中,f表示原图的灰度信息,w表示子图的灰度信息。s,t没有明确的表示方向。
对于相关性匹配中可能出现f和w对于幅度变化过于敏感的缺陷,一般在匹配过程中使用相关系数。
3、最佳统计分类器(主要是贝叶斯分类器)
答:1)贝叶斯分类器原理:
①若指定未知模式属于某一个样本模式类,而实际上未知模式不属于该样本模式类的概率是r,可以称r为平均失效率。
②若依次将未知模式指定为所有样本模式类之一,同时获取平均失效率r。最后获取最小的平均是效率对应匹配,得到的就是正确匹配。
2)高斯模式类的贝叶斯分类器:
由于贝叶斯分类器在计算平均是效率r时需要用到未知模式属于样本模式类的概率密度函数,这个函数需要估计得到,故贝叶斯分类器常采用接近真实情况的高斯概率密度函数。对应的贝叶斯分类器也就是高斯模式的贝叶斯分类器。
注意:高斯概率密度函数由模式类的平均向量和协方差矩阵指定。
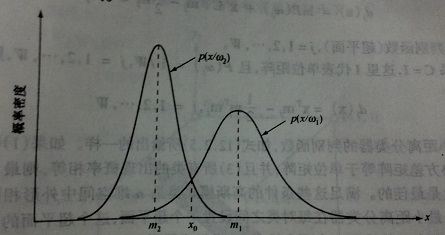
3)贝叶斯分类器决策边界获取(只介绍一维):
一维模式类的贝叶斯分类器决策边界:两个贝叶斯分类器的概率密度函数相交点即为决策边界;
如图:x=x0就是决策分解函数
4)应用:遥感图像分类,主要用于识别出河流、城市建筑、道路、乡村等目标。
4、神经网络
答:神经网络的识别即通过对训练集合进行训练得到前述所需的决策判别函数。
(1)感知器:感知器用于学习判别函数,将训练集合分为两个类别。模型(线性判别感知器)如下:
输入:一个模式向量x(x1,x2,..xn),用于表还是一个模式(对象)的特征量;
权重向量:w(w1,w2,...,wn),用于对输入进行预先修正;
激活函数:将求和值输出映射到最终的装置的函数,本模型中激活函数是门限函数;
本模型的判别函数:d(x)=∑Wi*Xi+Wn+1;d(x)大于0输出为正1,小于0输出位负1。
(2)感知器的训练分类
训练对象主要有两种:线性可分离的类与不可分离的类;
线性可分离类的训练算法:迭代算法;
不可分离的类训练算法:德尔塔规则的训练算法(如梯度下降算法)。
5、多层前馈神经网络模型
(1)模型如下:由模式向量作为输入,多个上述感知器构成的网络层,每层的权重向量、输出层构成。
上述每层网络的连接点(圆形)叫做神经元,类似前述感知器中的求和与激活函数(或叫做触发函数)的组合,具体可见图片上的详细神经元细节。只是神经元中的门限激活函数被S型激活函数(就是常说的sigmoid函数)代替;
(2)S型激活函数(sigmoid函数):
①、满足公式:

②、将上述激活函数表示成曲线:

③神经网络中实际的S型激活函数:
由前面神经元中S型激活函数的介绍,可知在神经网络中可以令输入函数:

神经网络的激活函数有很多种,除了sigmoid外还有tanh、relu及其改进型等。用一句话总结神经网络的激活函数就应该是:输出范围有限的非线性的可微单调函数。
6、神经网络各层节点数确定
答,如下,包括三部分:
(1)第一层神经元结点数=输入模式向量维数(输入模式向量维数根据每个模式信号归一化处理后得到的样本分量决定);
(2)最后一层神经元结点数=模式类的数量(最后一层神经元的输出结果就是对应各个模式类别);
(3)中间隐含层的节点数根据如下公式确定(中间层节点个数多少决定了网络结构好坏的关键):
Ns表示隐含层节点(隐含层节点数都一样),Nm表示分类数目,Ni表示输入特征向量维数。
(4)选定S型激活函数,必须满足下式(I为输入,O为输出,θj为偏差,θ0适用于控制S型激活函数形状的参数):

7、神经网络训练要点
答:主要包括:
(1)提取模式向量:提取各个类别图像的模式向量(如不变矩作为图像模式特征向量);
(2)模式向量标准化:将提取的模式向量标准化,是向量值都在[0,1]之间;
(3)计算模式类的期望输出:由模糊函数给定。对前述所得到每个模式向量进行模糊分类,得到的就是该模式向量对应的期望输出。模糊函数如下:
注:α和β需要根据实际情况进行选取。
(4)构造网络模型:后面以BP网络模型为例介绍了;
(5)训练:后面以BP学习为例介绍了;
(6)测试:一个输入向量经过训练好的网络,输出层得到的结果中具有最大值的类别就是神经网络判定的类别(这叫“竞争选择”)。
8、反向传播(BP)神经网络算法基础介绍
答:(1)BP网络训练原理:所谓的反向实质是指在前馈网络基础上,进行偏差的反向传播。从输出层开始根据反向路径调整每层权值(权值调整算法是梯度下降法),使得误差函数最小化就训练结束。
(2)输出的误差函数(又损失函数):
BP网络训练的目的是使得输出误差函数最小化,输出误差函数如下(期望与实际输出的误差平方):
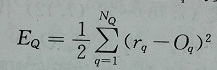
首先,对输出层进行权值调整。然后,根据网络连锁性,计算倒数第二层的权值调整量,……,直到完成对所有层的权值调整。
(3)权值调整规则(梯度下降法):
①、调整方式:先对输出层的权值向量进行调整,然后反向对倒数第二层权值进行调整,接着倒数第三层,……,直到完成对第一层神经元的权值向量进行调整;一遍调整结束后,对网络输入样本模式数据,得到输出层新的输出数据,使用误差函数进行计算,若误差函数未实现最小化,继续进行上一步骤的反向权值量调整。
②、权值调整量:
上述每一次的权值调整量设为△Wqp,根据如下公式对每一层进行调整:
即每次调整权值量是当前误差与权值的偏导数的某个比例,上述公式中p表示q的前一层,q代表当前层,η代表学习率。
这个权值调整公式可以根据输入函数、S型激活函数、误差函数化为实用的权值调整公式:
实际使用中就是根据该公式计算每一层权值的调整量,其中η为给定比例值且Op是上一层输出值,所以实际需要求解就是中间的梯度值δ((期望r与实际O误差量)*激活函数h的导数),因此这种调整方式属于梯度下降法。
具体关于梯度下降法可以参考:http://www.cnblogs.com/pinard/p/5970503.html
③、输出层和隐藏层权值调整量的不同:
有上述给定的权值调整量w=ηδO可知,每次计算调整量就需知道每个节点的期望输出r。这对于最后一个输出层是可以得到的,但是对于中间隐藏层却不可得到。因为中间层有很多节点,每个节点输出并不固定,中间层节点输出值是互相影响,综合作用最终结果的,所以无法设定中间层任何节点的期望值。故权值调整函数根据输出层和中间层不同,分为两种情况:
1°、输出层:直接使用上述给出的公式;
2°、中间隐藏层:η已给定,O可从网络中得到。因此主要改变梯度值δ的求解方式。改变求导变换,可以得到如下:
其中,δp是当前中间层的梯度值,δq是前一层的梯度值。
由于是方向调整,所以δq已经在前一次调整中得到了,所以就是已知的了。
9、BP学习具体步骤归纳
答:(1)主要有如下步骤:
①、权值和节点偏移的初始化(用随机值初始化);
②、给定输入矢量I(输入模式向量)和期望输出矢量r(期望输出由模糊函数计算给定,后面会介绍);
③、计算实际输出矢量(前向传播计算输出结果);
④、梯度计算(反向传播用损失函数计算梯度),分别分为输出层和隐藏层,如下图所示:
⑤、权值学习,即计算权值调整量(正向依次根据调整函数计算):
⑥、回到步骤②直到求出最优解(调整量小于阈值为止),然后根据上述结果构造如多层前馈神经网络模型所示的神经网络。
(2)更详细步骤参考下图:
10、BP算法的改进
答:上述权值调整公式中,η是固定值,表示学习率,其作用类似于比例调整。在权值趋近于最佳值时,较大的η可能会造成输出振荡。所以,改进型BP算法为了防止振荡,同时又保证较大的学习率,采用如下两种改进策略:
①、使用动态可变的学习率参数η;
②、向权值调整函数添加阻尼项β[Wqp(n)-Wqp(n-1)];
改进后的完整权值计算公式(第(n+1)次神经元p到q的权值调整):
11、AdBoost的基本原理
答:AdBoost是一个广泛使用的BOOSTING算法,其中训练集上依次训练弱分类器,每次下一个弱分类器是在训练样本的不同权重集合上训练。权重是由每个样本分类的难度确定的。分类的难度是通过分类器的输出估计的。
12、决策面的复杂性
答:(1)单超平面:单个感知器对目标的分类决策面是一个超平面,包括前面介绍的其他简单分类器的决策面也最多是一个单超平面。这种决策面只能做类似线性分割(即两种不同类互相之间没有混合),不能很好的分开混在一起的模式类;
(2)开、闭凸区域:由两层感知器构造而成的神经网络,生成的决策面就是开/闭凸区域。这种由两个或三个超平面构造而成的决策面可以分割一些混合在一起的模式类;
(3)任意形状的决策面:有多层感知器构造而成的神经网络,如上所述的多层前馈神经网络和多层BP神经网络,产生的决策面由多个不同的超平面构成,可以分割任意混合态的模式类;
如图:
第十章 其他
1、 Intel指令集中MMX、SSE、SSE2、SSE3和SSE4指的是什么?
答:(1)Intel指令集中MMX(Multi Media eXtension,多媒体扩展指令集)指令集是Intel公司于1996年推出的一项多媒体指令增强技术。MMX指令集中包括有57条多媒体指令,通过这些指令可以一次处理多个数据,在处理结果超过实际处理能力的时候也能进行正常处理,这样在软件的配合下,就可以得到更高的性能。MMX的益处在于,当时存在的操作系统不必为此而做出任何修改便可以轻松地执行MMX程序。但是问题也比较明显,那就是MMX指令集与X87浮点运算指令不能够同时执行,必须做密集式的交错切换才可以正常执行,这种情况就势必造成整个系统运行质量的下降;
(2)Intel指令集中SSE(Streaming SIMD Extensions,单指令多数据流扩展)指令集是Intel在Pentium 3处理器中率先推出的。
(3)Intel指令集中SSE2(Streaming SIMD Extensions 2,Intel官方称为SIMD 流技术扩展 2)指令集是Intel公司在SSE指令集的基础上发展起来的。相比于SSE,SSE2使用了144个新增指令,扩展了MMX技术和SSE技术,这些指令提高了广大应用程序的运行性能。
(4)Intel指令集中SSE3(Streaming SIMD Extensions 3,Intel官方称为SIMD 流技术扩展 3)指令集是Intel公司在SSE2指令集的基础上发展起来的。相比于SSE2,SSE3在SSE2的基础上又增加了13个额外的SIMD指令。SSE3 中13个新指令的主要目的是改进线程同步和特定应用程序领域,例如媒体和游戏。
(5)Intel指令集中SSE4 (Streaming SIMD Extensions 4) 是英特尔自从SSE2之后对ISA扩展指令集最大的一次的升级扩展。新指令集增强了从多媒体应用到高性能计算应用领域的性能,同时还利用一些专用电路实现对于特定应用加速。Intel SSE4 由一套全新指令构成,旨在提升一系列应用程序的性能和能效。Intel SSE4 构建于英特尔64指令集架构(Intel64 ) (ISA)。
2、 并行计算有哪些实现方式?
答:并行计算就是在并行计算或分布式计算机等高性能计算系统上所做的超级计算。实现方式有:单指令多数据流SIMD、对称多处理机SMP、大规模并行处理机MPP、工作站机群COW、分布共享存储DSM多处理机。