- 1安装docker compose_安装docker-compose
- 2【UE4】如何获取/下载虚幻4(Unreal Engine4)源码
- 3利用Pytorch实现ResNet网络
- 4python中使用多进程multiprocessing并获取子进程的返回值_multiprocessing开启另一线程进行实例化对象怎么返回到主线程
- 5Maven 仓库国内镜像源收藏_maven 厂库国内镜像
- 6【批处理脚本】-2.1-测试IP连接命令ping_批处理获取ip是否通
- 7学习笔记8-python skimage图像处理(实例演示-代码讲解)_rough-wall.png墙壁图像处理skimage
- 83D Gaussian Splatting的使用_训练3d gaussian splatting模型步骤
- 9mvn offline 离线安装依赖和生成jar包
- 10windows安装pip工具_qlyd1yvx
14、三维表面重建-DeepSDF
赞
踩
简介
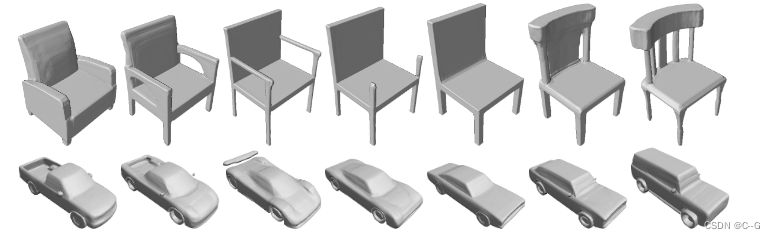
传统的表面重建技术中,SDF是基于离散化体素对物体或者场景表面的一种表达,而现实中表面是连续的,DeepSDF是一种学习过的连续符号距离函数(SDF)表示一类形状,可以从部分和有噪声的3D输入数据中进行高质量的形状表示、插值和补全
贡献点
- 提出了基于连续隐式曲面的生成式形状条件三维建模的公式
- 基于概率自动解码器的三维形状学习方法
- 在形状建模和完成中的演示和应用
Related work
3D物体形状的表示可以分成3类:基于点,mesh和voxel的方法
-
Point-based
点云是一种轻量级的3D表示,它与许多传感器(如激光雷达、深度相机)提供的原始数据紧密匹配,因此很适合应用3D学习,适合于做分类分割检测的工作,不能描述拓扑结构,不适合生产水密表面 -
Mesh-based
各种方法用预定义的模板网格来表示形状相似的物体,如可变形的人体部分,模板网格使用方便,自然提供了三维对应关系,但只能对网格拓扑结构固定的形状进行建模 -
Voxel-based
体素,用数值的3D网格非参数地描述体积,目前的方法只能处理低分辨率(1283或以下),不能保存精细的形状细节,高保真形状明显不同,因为在渲染时它们的法线并不光滑,可拓展性不强,当然有很多学者提出使用八叉树或者voxel hash的方法,但是只是在数据结构层面的改进,自身固有的缺陷(分辨率)没有解决。
实现思路

SDF是一个连续函数,对于给定的空间点,输出该点到最近表面的距离,其符号编码是在watertight surface的内部(负)还是外部(正):
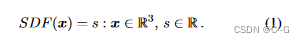
s > 0是外部,s < 0是内部,s = 0是表面。
核心思想是利用深度神经网络从点样本直接回归连续的SDF,训练后的网络可预测给定查询位置的SDF值,这样的话就可以学习任意精度的全连续形状函数。
实际逼近的精度受到指导决策边界的点样本数量有限和计算能力有限网络容量有限的限制
可以联想到NeRF也是通过在光线上采样做积分的方式完成渲染
single shape deepSDF
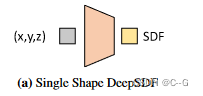
给定一个目标形状,得到一组由3D点样本及其SDF值组成的数据
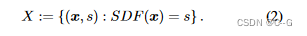
在训练集S上训练多层全连接神经网络 f θ f_θ fθ 的参数 θ,使 f θ f_θ fθ 在目标域 Ω 中成为给定SDF的良好逼近器
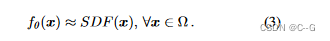
X 中各点的预测 和 真实SDF值在以下L1损失函数下的损失总和最小来完成的
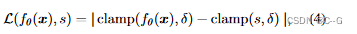
clamp(x, δ) := min(δ, max(−δ, x)),同时引入了一个参数 δ 来控制距离,较大的 δ 值允许快速射线追踪,因为每个样本给出了安全步长信息。较小的 δ 值可用于将网络容量集中在近地表细节。
实验中使用 δ = 0. 1和一个由8个全连接层组成的前馈网络,每个层都应用了dropouts。所有内层均为512维,具有ReLU非线性,输出非线性回归SDF值为tanh,使用Adam优化器。
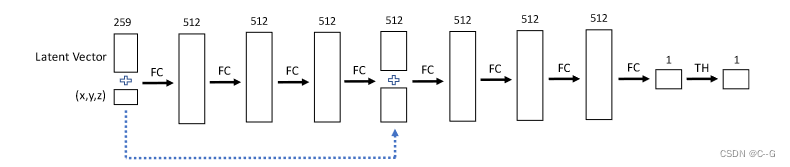
coded shape deepSDF
上面方法只能对单一形状进行重建,因为模型没有包含任何shape的信息。
下面将shape用latent vector的方式作为网络的输入,以此适应多种形状,每一种形状都有一个对应的code
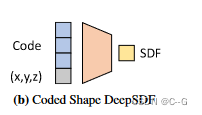
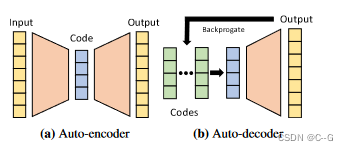
自动解码器直接接受潜在向量作为输入。在训练开始时,给每个数据点分配一个随机初始化的潜在向量,并通过标准反向传播对潜在向量和解码器权重进行优化。
在推理过程中,译码器的权值是固定的,并估计出一个最优潜在向量。
在概念上,将这个潜在向量映射到一个连续的SDF表示的3D形状
形式上,对于某个由 i 索引的形状,
f
θ
f_θ
fθ 现在是一个潜在代码
z
i
z_i
zi 和一个查询3D位置 x 的函数,并输出形状的近似SDF
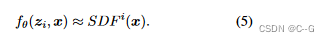
概率公式化
由于Auto-encoders和encoder-decoder网络的瓶颈特征容易形成自然潜变量表示,因此被广泛用于表示学习
实验表明auto-decoder更好生成高质量3D生成模型,为此开发了一个概率公式来训练和测试自动解码器,它自然地引入了潜在空间正则化来改进泛化。
给定一个用符号距离函数(SDF)表示的N个形状的数据集,有一组 K 点样本及其符号距离值
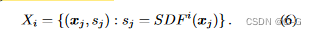
对于自动解码器,由于没有编码器,每个潜在代码 z i z_i zi 都与训练形状 X i X_i Xi 配对。给定形状SDF样本 X i X_i Xi 的后验概率为
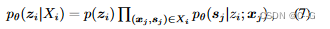
其中θ参数化SDF似然, p ( z i ) p(z_i) p(zi) 假设服从zero-mean multivariate-Gaussian分布
通过一个深度前馈网络 f θ ( z i , x j ) f_θ(z_i, x_j) fθ(zi,xj) 表示SDF似然,假设似然形式为
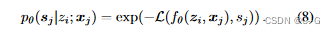

最终得到训练阶段的优化目标
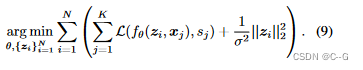
在测试的时候,参数 θ 不动,可以通过最大值后验估计来估计形状 X i X_i Xi 的形状代码 z i z_i zi
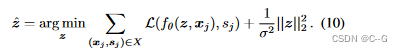
至关重要的是,这个公式对于任意大小和分布的SDF样本X是有效的,因为对于每个SDF样本,损失相对于z的梯度可以单独计算。这意味着DeepSDF可以处理任何形式的局部观测,如深度图。这是与自编码器框架相比的一个主要优势,自编码器要求类似于训练数据的测试输入
为了纳入潜在形状码,将码向量和样本位置进行叠加,并将其输入到之前所述的输入层和第4层相同的全连接NN中。再次使用Adam优化器。潜在向量z从N(0, 0.012)随机初始化。