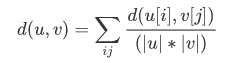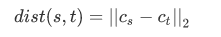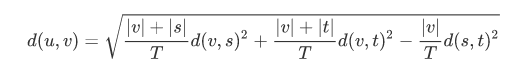聚类算法（五）——层次聚类 linkage （含代码）_层次聚类模型评价代码

聚类算法相关：

聚类算法（一）——DBSCAN

聚类算法（二）—— 优缺点对比

聚类算法（三）—— 评测方法1

聚类算法（三）—— 评测方法2

聚类算法（三）—— 评测方法3(代码）

聚类算法（四）—— 基于词语相似度的聚类算法（含代码）

聚类算法（五）——层次聚类 linkage （含代码）

聚类算法（六）——谱聚类 （含代码）

聚类算法（七）—— Kmeans

一　原理

基本工作原理
给定要聚类的N的对象以及N*N的距离矩阵(或者是相似性矩阵), 层次式聚类方法的基本步骤(参看S.C. Johnson in 1967)如下:
1.     将每个对象归为一类, 共得到N类, 每类仅包含一个对象. 类与类之间的距离就是它们所包含的对象之间的距离.

2.     找到最接近的两个类并合并成一类, 于是总的类数少了一个.
3.     重新计算新的类与所有旧类之间的距离.
4.     重复第2步和第3步, 直到最后合并成一个类为止(此类包含了N个对象).
根据步骤3的不同, 可将层次式聚类方法分为几类: single-linkage, complete-linkage 以及 average-linkage 聚类方法等.

single-linkage 聚类法(也称 connectedness 或 minimum 方法)：

类间距离等于两类对象之间的最小距离，若用相似度衡量，则是各类中的任一对象与另一类中任一对象的最大相似度。

complete-linkage 聚类法 (也称 diameter 或 maximum 方法)：

组间距离等于两组对象之间的最大距离。

average-linkage 聚类法：

组间距离等于两组对象之间的平均距离。

average-link 聚类的一个变种是R. D'Andrade (1978) 的UCLUS方法, 它使用的是median距离, 在受异常数据对象的影响方面, 它要比平均距离表现更佳一些.

参考： http://blog.sciencenet.cn/blog-1271266-858703.html  

 

 

二　函数原型

 scipy.cluster.hierarchy.linkage(y, method='single', metric='euclidean', optimal_ordering=False)

参考自： https://blog.csdn.net/Tan_HandSome/article/details/79371076?utm_source=blogxgwz9

１.１　method 

主要是 method 这个参数

• method = ‘single’

            d(u,v) = min(dist(u[i],u[j]))

对于u中所有点i和v中所有点j。这被称为最近邻点算法。

• method = 'complete'

             d(u,v) = max(dist(u[i],u[j]))

  对于u中所有点i和v中所有点j。这被称为最近邻点算法。

• method = 'average'

                

|u|，|v|是聚类u和v中元素的的个数，这被称为UPGMA算法（非加权组平均）法。

• method = 'weighted'

            d(u,v) = (dist(s,v) + dist(t,v))/2

u是由s和t形成的，而v是森林中剩余的聚类簇，这被称为WPGMA（加权分组平均）法。

• method = 'centroid'

            

Cs和Ct分别为聚类簇s和t的聚类中心，当s和t形成一个新的聚类簇时，聚类中心centroid会在s和t上重新计算。这段聚类就变成了u的质心和剩下聚类簇v的质心之间的欧式距离。这杯称为UPGMC算法（采用质心的无加权paire-group方法）。

 

• method = 'median'

  当两个聚类簇s和t组合成一个新的聚类簇u时，s和t的质心的均值称为u的质心。这被称为WPGMC算法。

• method = 'ward' （沃德方差最小化算法）

新的输入d(u,v)通过下式计算得出，

        

u是s和t组成的新的聚类，v是森林中未使用的聚类。T = |v|+|s|+|t|，|*|是聚类簇中观测值的个数。

注意：当最小距离在一个森林中成对存在时，即有多个最小距离的时候，具体的实现要看MATLAB的版本（因为这个函数是从matlab里面copy过来的）。

１.２参数：

y：nump.ndarry。是一个压缩距离的平面上三角矩阵。或者n*m的观测值。压缩距离矩阵的所有元素必须是有限的，没有NaNs或infs。

method：str，可选。

metric：str或function，可选。在y维观测向量的情况下使用该参数，苟泽忽略。参照有效距离度量列表的pdist函数，还可以使用自定义距离函数。

optimal_ordering:bool。若为true，linkage矩阵则被重新排序，以便连续叶子间距最小。当数据可视化时，这将使得树结构更为直观。默认为false，因为数据集非常大时，执行此操作计算量将非常大。

三　代码

简单版

 
from scipy.cluster.hierarchy import dendrogram, linkage,fcluster
from matplotlib import pyplot as plt
X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]]
# X = [[1,2],[3,2],[4,4],[1,2],[1,3]]
Z = linkage(X, 'ward')
f = fcluster(Z,4,'distance')
fig = plt.figure(figsize=(5, 3))
dn = dendrogram(Z)

复杂一点的，对于词语聚类，采用word2vec 聚类（也可以采用fasttext的句子向量） 参见：聚类算法（四）—— 基于词语相似度的聚类算法（含代码）

 

from scipy.spatial.distance import pdist
from scipy.cluster.hierarchy import dendrogram,linkage, fcluster
import os
import pickle
import numpy

采用词向量计算 

keywords = [] # 这里列上想要聚类的词语或句子
embedding_file = '' # embedding 模型文件
embedding_model2 = Embedding(embedding_file, 200, type='w2v')
vec = [embedding_model2.get_word_embedding(x) for x in keywords]  # get_word_embedding 参见聚类算法(四) 或者直接替换为自己的词向量算法，或特征向量
 
arr = numpy.array(vec)
dist = pdist(arr, metric='cosine')
 
row_clusters = linkage(dist, method ='median')  # centroid、median、ward只能定义在欧氏距离计算中。如果预先将y计算的距离传进来，那么要确保是用欧式距离计算的，否则将会导致错误的计算结果
 
 

上面代码也可以替换为TfidfVectorizer

import jieba.posseg as pseg
from sklearn.feature_extraction.text import TfidfVectorizer
from scipy.spatial.distance import pdist
import os
import pickle
 
cv = TfidfVectorizer(binary=False, decode_error='ignore')
vec = cv.fit_transform(feature) # feature 为文本切词后的list
arr = vec.toarray()
dist = pdist(arr, metric=metric)
row_clusters = linkage(dist, method=method)

结果处理 

data = {"file_names_list": keywords, "row_clusters": row_clusters, "dist": dist}
result = get_cluster_result(data, 0.5)
count = 1
for item in result:
    for e in item['file_names']:
        print("{}\t{}\t{}\t{}".format(e, count, item["max_value"], len(item["file_names"])))
    count += 1

 结果格式转化函数

 
def get_cluster_result(data, threshold):
    file_names_list = data["file_names_list"]
    row_clusters = data["row_clusters"]
    dist = data["dist"]
 
    max_value = 0
    for row in row_clusters:
        if row[2] > max_value:
            max_value = row[2]
    labels = fcluster(row_clusters, t=threshold * max_value, criterion="distance")
 
    cluster_dict = dict()
    for i in range(len(file_names_list)):
        if labels[i] not in cluster_dict:
            cluster_dict[labels[i]] = []
        cluster_dict[labels[i]].append({"file_name": file_names_list[i], "index": i})
 
    k = 0
    m = len(file_names_list)
    ij2index = dict()
    for i in range(0, m):
        for j in range(i + 1, m):
            ij2index["i:{}j:{}".format(i, j)] = k
            k += 1
 
    result = []
    for key, value in cluster_dict.items():
        index = []
        file_names = []
        max_value = 0
        for item in value:
            index.append(item["index"])
            file_names.append(item["file_name"])
 
        if len(index) > 1:
            for i in range(len(index)):
                for j in range(i+1, len(index)):
                    temp = dist[ij2index["i:{}j:{}".format(index[i], index[j])]]
                    if temp > max_value:
                        max_value = temp
            result.append({"file_names": file_names, "max_value": 1-max_value})
        else:
            result.append({"file_names": file_names, "max_value": 1})
    result.sort(key=lambda o: -len(o["file_names"]))
 
    return result