【信息论】熵、交叉熵、互信息、KL散度（相对熵）_kl分歧

熵

也称为信息熵或香农熵。

数学

对于离散随机变量X，可能的结果（状态）x_1，...，x_n，以比特为单位的熵定义为：

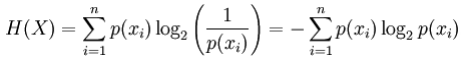
其中p（x_i）是X的第i个结果的概率。

应用

 

 

 

• 熵用于自动决策树构造。在树构建的每个步骤中，使用熵标准来完成特征选择。
• 基于最大熵原理的模型选择是从具有最高熵的竞争模型中得出的最佳状态。

交叉熵

直观

交叉熵用于比较两个概率分布。它告诉我们两个分布是如何相似的。

数学

在相同的结果集上定义的两个概率分布p和q之间的交叉熵由下式给出：

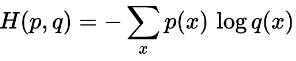
应用

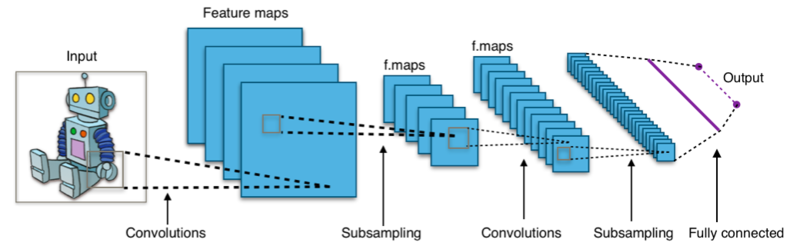
基于卷积神经网络的分类器通常使用softmax层作为使用交叉熵损失函数训练的最终层。

 

 

 

 

 

• 交叉熵损失函数广泛用于逻辑回归等分类模型。随着预测偏离真实输出，交叉熵损失函数增加。
• 在诸如卷积神经网络的深度学习架构中，最终输出“softmax”层经常使用交叉熵损失函数。

相互信息

直观

相互信息是两种概率分布或随机变量之间相互依赖性的度量。它告诉我们有关一个变量的信息是由另一个变量承载的。

相互信息捕获随机变量之间的依赖性，并且比香草相关系数更普遍，后者仅捕获线性关系。

数学

两个离散随机变量X和Y的相互信息定义为：

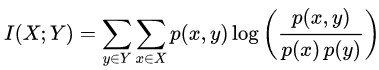
其中p（x，y）是X和Y的联合概率分布，p（x）和p（y）分别是X和Y的边际概率分布。

应用

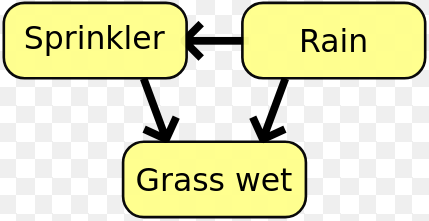
在贝叶斯网络中，可以使用互信息确定变量之间的关系结构。

 

 

 

 

• 特征选择：可以使用互信息，而不是使用相关性。相关性仅捕获线性依赖性并忽略非线性依赖性，但相互信息不会。零的相互独立性保证随机变量是独立的，但零相关不是。
• 在贝叶斯网络中，互信息用于学习随机变量之间的关系结构，并定义这些关系的强度。

Kullback Leibler（KL）分歧

也称为相对熵。

直观

KL分歧是发现两个概率分布之间相似性的另一种方法。它衡量一个分布与另一个分布的差异。

假设，我们有一些数据和真正的分布，它是'P'。但我们不知道这个'P'，所以我们选择一个新的分布'Q'来估算这些数据。由于“Q”只是一个近似值，因此无法将数据逼近“P”，并且会发生一些信息丢失。这种信息丢失由KL分歧给出。

'P'和'Q'之间的KL差异告诉我们当我们尝试用'Q'逼近'P'给出的数据时，我们失去了多少信息。

数学

来自另一概率分布P的概率分布Q的 KL偏差定义为：

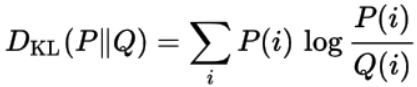
应用

KL散度通常用于无监督机器学习技术变分自动编码器。

 

原文：https://towardsdatascience.com/must-know-information-theory-concepts-in-deep-learning-ai-e54a5da9769d