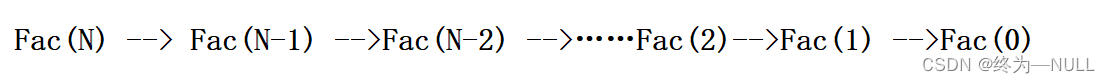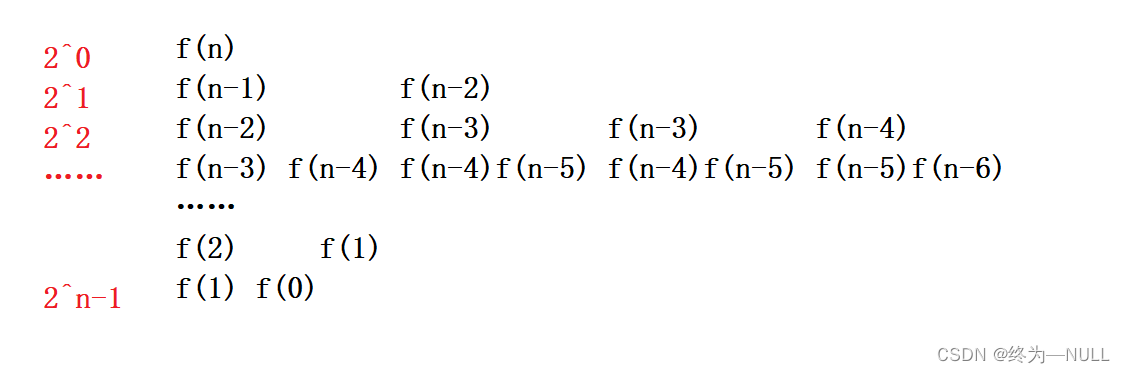数据结构之算法复杂度篇_数据结构的算法复杂度

要努力，但是不要急。繁花锦簇，硕果累累都需要过程 。

目录

前言：

1.什么是数据结构？

2.什么是算法？

3.算法的复杂度

1.概念：

2.时间复杂度：

3.空间复杂度：

4.常见的复杂度对比：

4.复杂度的oj练习：

5.总结：

---

前言：

在程序段运行的时候，我们总会去关注程序的执行效率，因为程序的执行效率直接影响实际中的用途，而执行效率又是时间复杂度和空间复杂度来决定的，接下来开始逐一剖析程序的算法复杂度。

1.什么是数据结构？

数据结构(Data Structure)是计算机存储、组织数据的方式，指相互之间存在一种或多种特定关系的数据元素的集合。在内存中管理数据，增删查改。

2.什么是算法？

算法(Algorithm):就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤，用来将输入数据转化成输出结果。

3.算法的复杂度

1.概念：

算法的复杂度实质算法在编写成可执行程序，运行时需要耗费的时间资源和空间资源，因此通常通过时间复杂度和空间复杂度来衡量一个算法的好坏。

2.时间复杂度：

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

举例1：

//计算Func1函数中count执行的次数：

void Func1(int N)
{
	int count = 0;
	for (int i = 0; i < N; ++i)
	{
		for (int j = 0; j < N; ++j)
		{
			++count;
		}
	}
	for (int k = 0; k < 2 * N; ++k)
	{
		++count;
	}
	int M = 10;
	while (M--)
	{
		++count;
	}
    printf("%d\n",count);
}

Func1的执行次数：

F(N) = N^2 + 2*N + 10;

实际中计算复杂度的时候，其实并不需要计算精确的执行次数，而只需要计算大概的执行次数，因此在这里我们使用大O的渐近表示法

大O的渐近表示法：

是用于描述函数渐近行为的数学符号

1、用常数1取代运行时间中的所有加法常数。

void Func4(int N) 
{ 
	int count = 0;
	for (int k = 0; k < 100; ++k) 
	{ 
		++count; 
	} 
	printf("%d\n", count);
}

Fun4函数的时间复杂度就是O(1) 用1来代表常数次

2、在修改后的运行次数函数中，只保留最高阶项。

上述Func1函数的时间复杂度就是O(N^2)

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

void Func2(int N)
{ 
	int count = 0;
	for (int k = 0; k < 2 * N; ++k)
	{
		++count;
	} 
	int M = 10;
	while (M--)
	{
		++count; 
	} 
	printf("%d\n", count); 
}

Func2函数的时间复杂度去除相乘的常数，就是O(N)

练习1：

// 计算Func3的时间复杂度？
void Func3(int N, int M)
{ 
	int count = 0; 
	for (int k = 0; k < M; ++k)
	{ 
		++count; 
	} 
	for (int k = 0; k < N; ++k)
	{ 
		++count;
	} 
	printf("%d\n", count);
}

Fun3函数的复杂度O(M+N)

M远大于N  复杂度就是O(M)

N远大于M  复杂度就是O(N)

M和N一样大，复杂度就是O(M)或者是O(N)

练习2：

int BinarySearch(int* a, int n, int x)
{
	assert(a);
	int begin = 0;
	int end = n-1; 
	while (begin <= end)
	{
		int mid = (begin + end) / 2;
		if (a[mid] < x)
			begin = mid + 1;
		else if (a[mid] > x)
			end = mid - 1;
		else
			return mid;
	}
	return -1;
}

二分查找：每查找一次，查找区间个数少一半（除2）

N/2/2/2/2/2/2……=1

假设最坏的情况查找了x次： N = 2^x

x = log2N

所以二分查找函数的时间复杂度为O(log2N)

练习3：

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N) 
{ 
	if (0 == N) 
		return 1;  
	return Fac(N - 1) * N; 
}

所以Fac函数的时间复杂度为O(N) 

练习4：

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{ 
	if (N < 3) return 1;
	return Fib(N - 1) + Fib(N - 2);
}

时间复杂度==执行次数

2^0 + 2^1 + 2^2 + …… +2^n-1 ==F(N)

通过错位相减法计算得到F(N) = 2^n -1

所以斐波那契递归函数的时间复杂度为O(2^N) 

3.空间复杂度：

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 

空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。

例1：

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{
	assert(a); 
	for (size_t end = n; end > 0; --end)
	{ 
		int exchange = 0;
		for (size_t i = 1; i < end; ++i) 
		{ 
			if (a[i - 1] > a[i]) 
			{ 
				Swap(&a[i - 1], &a[i]);
				exchange = 1; 
			} 
	    }  
		if (exchange == 0) 
		break; 
	}
}

使用了常数个变量，所以空间复杂度为O(1)

例2：

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n) 
{ 
	if (n == 0) 
		return NULL;  
        long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
		fibArray[0] = 0; 
		fibArray[1] = 1; 
		for (int i = 2; i <= n; ++i) 
		{
			fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
		}  
         return fibArray; 
}

动态开辟了一个大小为n的数组，所以空间复杂度为O(N)

例3：

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
	if (N == 0)
		return 1;
	return Fac(N - 1) * N;
}

递归调用了n次，每次调用时开辟一个栈帧，每个栈帧中有常数个变量，递归的深度为N,所以递归完之后空间复杂度为O(N)

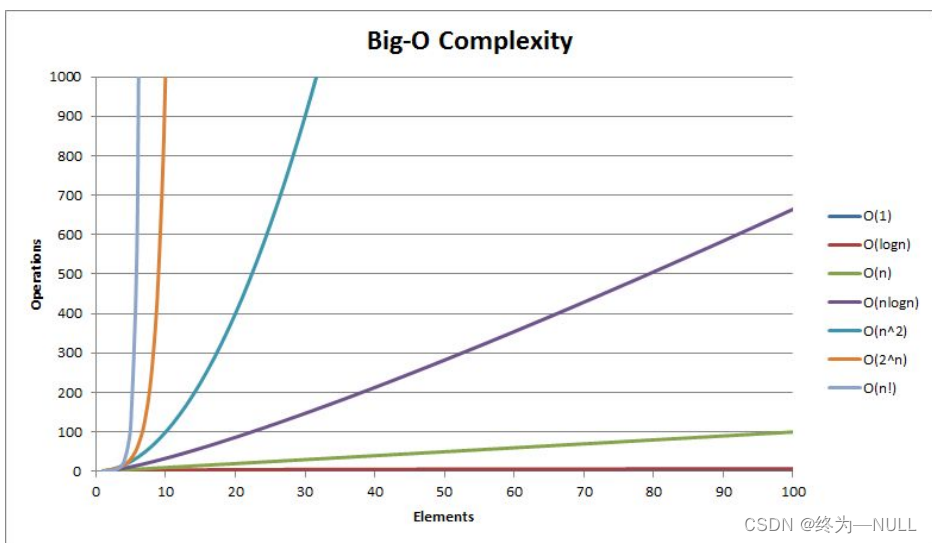
4.常见的复杂度对比：

随着元素个数的增加。程序的执行次数变化对比 

4.复杂度的oj练习：

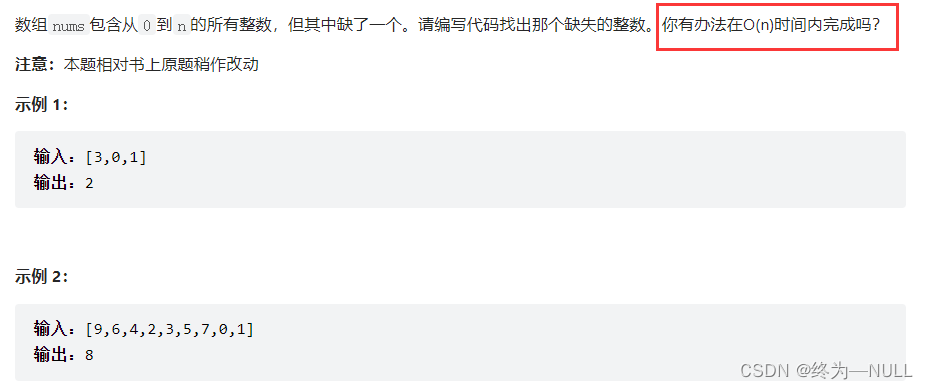
1.消失数字的练习：https://leetcode.cn/problems/missing-number-lcci/

题目描述：

解法1：

通过0~numsSize与数组中的每个元素进行异或，异或的特点是相同为0，所以最后剩下的元素一定是那个数组中没有的那个元素 

int missingNumber(int* nums, int numsSize)
{
    int i = 0;
    int n = 0;
    for(i=0; i<=numsSize; i++)
    {
        if(i < numsSize)
        {
             n ^= nums[i];
        }
        n ^= i;
    }
    return n;
}

解法2：

0~numsSize的数字相加减去数组中每个元素的相加之和，它们的差值就是消失的那个数字：

int missingNumber(int* nums, int numsSize)
{
    int i = 0;
    int sum1 = 0;
    int sum2 = 0;
    for(i=0; i<=numsSize; i++)
    {
        sum1 += i;
    }
    for(i=0; i<numsSize; i++)
    {
        sum2 += nums[i];
    }
    return sum1 - sum2;
}

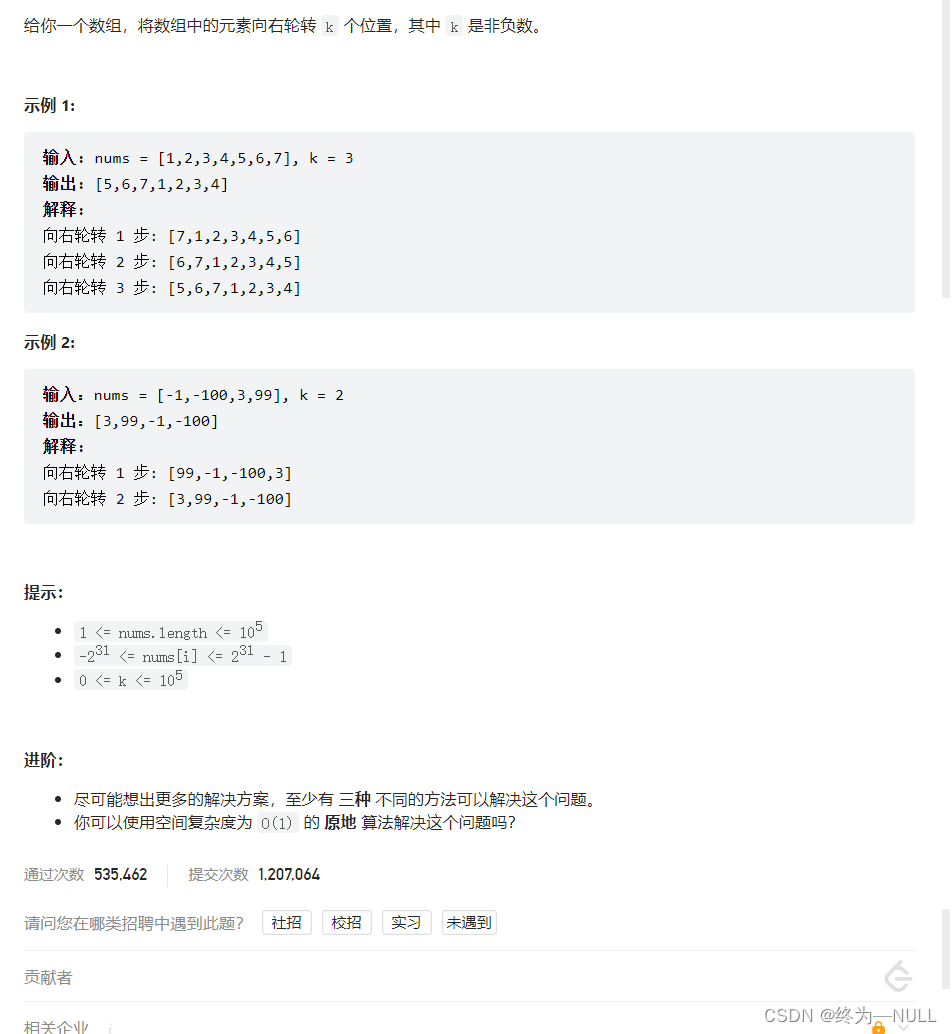
2.旋转数组练习：https://leetcode.cn/problems/rotate-array/

题目描述：

解法1：

先使用一个临时变量将最后一个数字保存起来，然后从后往前一次向后挪动一个数据，重复执行k次

void rotate(int* nums, int numsSize, int k)
{
    if (k >= numsSize)
    {
        k %= numsSize;
    }
    int i = 0;
    int j = 0;
    for (i = 0; i < k; i++)
    {
        int tmp = nums[numsSize - 1];
        for (j = numsSize - 1; j >= 1; j--)
        {
            nums[j] = nums[j - 1];
        }
        nums[0] = tmp;
    }
}

解法1时间复杂度为O(N^2),超出时间限制，不满足题目要求 

解法二：开辟一个新的数组将后k个数，从前往后存放到新开辟的数组中，然后将剩下的数依次向后存放，最后开辟数组中的元素拷贝到原来的数组中：

void rotate(int* nums, int numsSize, int k)
{
    if(k >= numsSize)
    {
        k %= numsSize;
    }
    int*p=(int*)malloc(sizeof(int)*numsSize);
    int pos = 0;
    int i = 0;
    for(i=0; i<k; i++)
    {
        p[pos++] = nums[numsSize-k+i];
    }
    for(i=0; i<numsSize-k; i++)
    {
        p[pos++] = nums[i];
    }
    for(i=0; i<numsSize; i++)
    {
        nums[i] = p[i];
    }
    free(p);
    p = NULL;
}

解法2：时间复杂度为O(N),空间复杂度为O(N),满足题目要求

解法3：先将旋转的数字逆置，再将剩下的数字逆置，最后整齐逆置：

void reverse(int arr[],int left,int right)
{
    while(left < right)
    {
        int tmp = arr[left];
        arr[left] = arr[right];
        arr[right] = tmp;
        left++;
        right--;
    }
 
 
}
void rotate(int* nums, int numsSize, int k)
{
    if(k >= numsSize)
    {
        k %= numsSize;
    }
    reverse(nums,numsSize-k,numsSize-1);
    reverse(nums,0,numsSize-k-1);
    reverse(nums,0,numsSize-1);
}

解法3的时间复杂度为O(N),空间复杂度为O(1)

5.总结：

以上就是关于数据结构入门之算法复杂度篇，通过举例详解了算法时间复杂度和空间复杂度的对程序的影响，为以后代码的优化提供了思路，希望能够帮助到你！