激光雷达SLAM简介

激光雷达

激光雷达主要包括激光发射、接收、扫描器、透镜天线和信号处理电路组成。

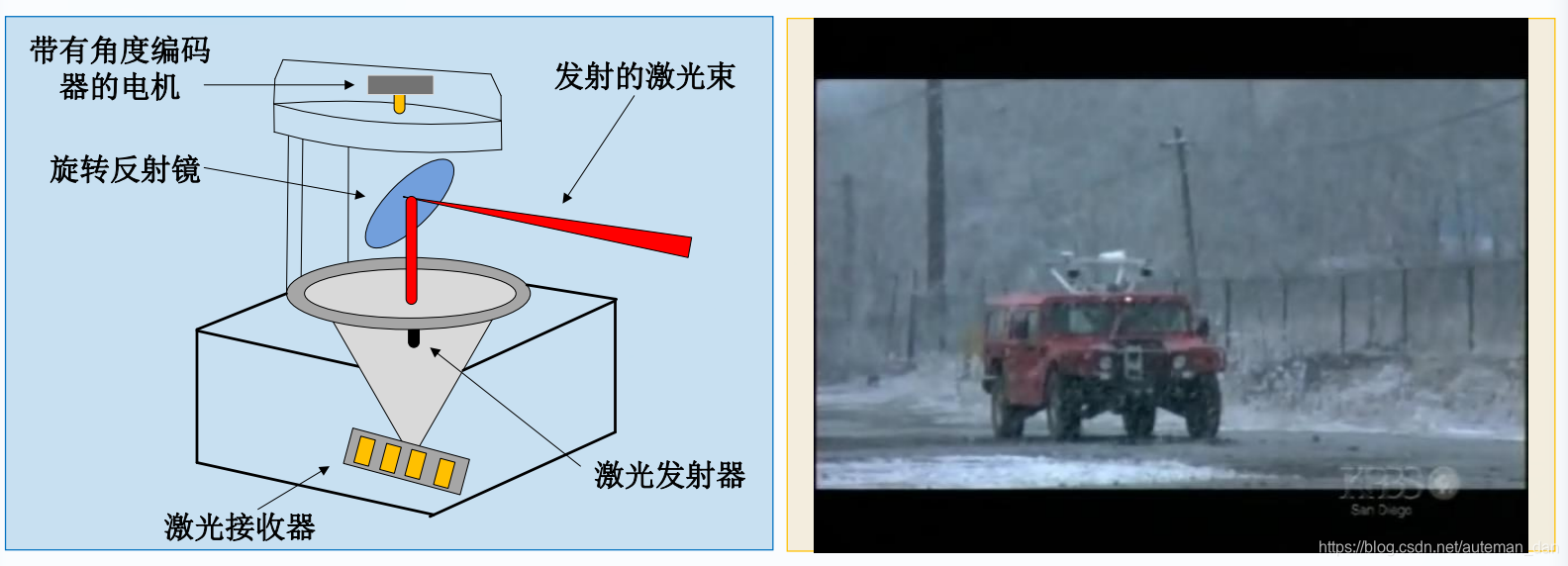
激光SLAM简介

Simultaneous localization and mapping(SLAM)， 实时定位与建
图。

1. localization: 在给定地图的情况下，估计机器人的位姿
2. Mapping: 在给定机器人定位的情况下，估计环境地图
3. SLAM: 同时估计机器人的位姿和环境地图

机器人导航包括建图、定位、路径规划等主要步骤。其中第一步的建图与定位是密不可分的。在某些场景中，我们可以通过差分GPS等方法获取机器人的绝对位姿，此时将传感器接收到的数据按照机器人的绝对位姿投影到世界坐标系就可以完成建图。也就是说要建图必须已知机器人的定位，而定位则需要有一张有足够精度的地图，对于无法获取机器人绝对位姿的情况，SLAM问题本质上是一个鸡生蛋、蛋生鸡的问题。我的理解是SLAM核心是定位。目标是建图。

SLAM的定义与分类

根据传感器分类

根据优化方法分类（状态估计）

激光雷达SLAM流程

数据处理

1.里程计标定:
（1）机械标称值不代表实际值，实际误差可能较大
（2）里程计的精度对于机器人定位和建图至关重要
2.激光雷达运动畸变去除
（1）激光雷达采集一帧的数据需要时间，机器人在这段时间内的运动会导致畸变
（2）运动畸变会影响匹配精度

帧间匹配–核心部分

1. ICP: 迭代最近邻
   PI-ICP 点到线迭代最近邻
   NICP 法向量迭代最近邻
2. CSM: 暴力迭代
3. NDT: Normal Distance Transform
4. Optimization-Based
5. Feature-Based
   从视觉得到启发，LOAM系列

回环检测

后端优化

1.高斯牛顿

2.Levenberg-Marquardt(LM)

激光雷达SLAM输入

1. IMU数据
2. 里程计数据
3. 2D激光雷达数据

激光SLAM的输出

1.占用栅格地图 2D SLAM
2. 点云地图 3D SLAM
2.机器人的轨迹或者位姿图

激光SLAM的帧间匹配方法

激光SLAM的发展

Filter-based

Graph-based

激光SLAM的趋势–与视觉融合

视觉提供的信息

1. 高精度的里程信息
2. 信息量丰富的视觉地图

融合解决的问题

1. 环境变化
2. 几何结构相似环境
3. 建图的操作复杂
4. 全局定位
5. 地面材质的变化
6. 机器人载重的变化

激光SLAM中的问题

1. 退化环境(Degeneration Environment)
2. 地图的动态更新(Map Updata)
3. 全局定位(Global Localization)
4. 动态环境定位(Dynamic Localization)

数学基础

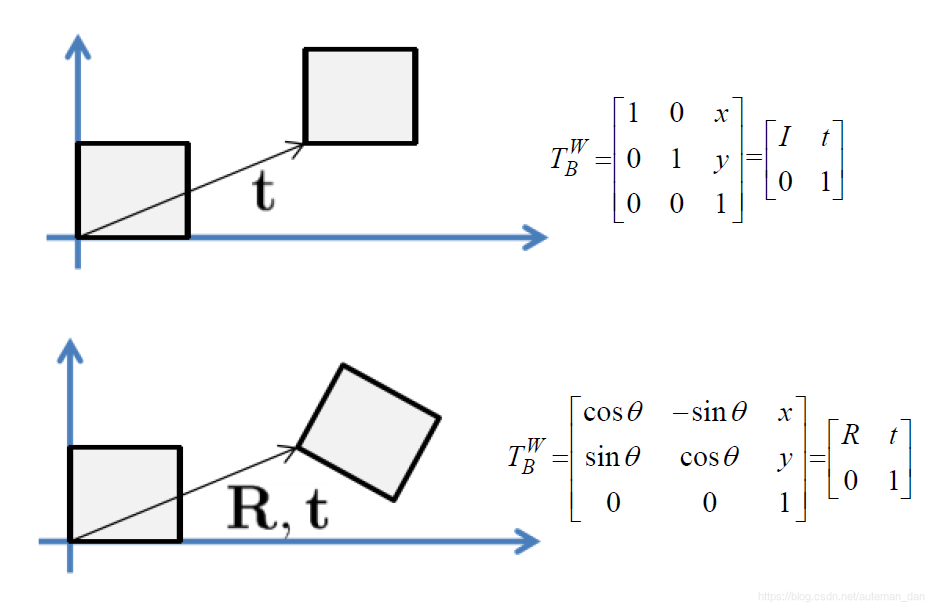
位姿表示和转换矩阵

位姿表示

机器人在坐标系中的坐标：
$$(x,y,\theta )$$
机器人坐标系B到坐标系W的转换矩阵：
T B W = [ c o s θ − s i n θ x s i n θ c o s θ y 0 0 1 ] = [ R t 0 1 ] T_B^W=

$$\begin{bmatrix} cos\theta & -sin\theta & x \\ sin\theta & cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}$$ = $$\begin{bmatrix}R & t \\ 0 & 1\end{bmatrix}$$ TBW​=⎣⎡​cosθsinθ0​−sinθcosθ0​xy1​⎦⎤​=[R0​t1​]

主动旋转(向量旋转)

旋转矩阵: 表示某一个物理量在不同坐标系下的表示。
R ( θ ) = [ c o s θ − s i n θ s i n θ c o s θ ] R(\theta) =

$$\begin{bmatrix}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}$$ R(θ)=[cosθsinθ​−sinθcosθ​]

被动旋转(坐标系旋转)

x w = a [ c o s θ s i n θ ] + b [ − s i n θ c o s θ ] x_w = a

$$\begin{bmatrix}cos\theta \\ sin\theta \end{bmatrix}$$ +b $$\begin{bmatrix}-sin\theta \\ cos\theta \end{bmatrix}$$ xw​=a[cosθsinθ​]+b[−sinθcosθ​]

即 x w = [ c o s θ − s i n θ s i n θ c o s θ ] x_w =

$$\begin{bmatrix}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}$$ xw​=[cosθsinθ​−sinθcosθ​]

旋转矩阵：

R B W = [ c o s θ − s i n θ s i n θ c o s θ ] R_B^W =

$$\begin{bmatrix}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}$$ RBW​=[cosθsinθ​−sinθcosθ​]

坐标系B在坐标系W中的坐标：
$$(x,y,\theta )$$
坐标系B到坐标系W的转换矩阵：
T B W = [ c o s θ − s i n θ x s i n θ c o s θ y 0 0 1 ] = [ R t 0 1 ] T_B^W =

$$\begin{bmatrix}cos\theta & -sin\theta & x \\ sin\theta & cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}$$ = $$\begin{bmatrix} R & t \\ 0 & 1\end{bmatrix}$$ TBW​=⎣⎡​cosθsinθ0​−sinθcosθ0​xy1​⎦⎤​=[R0​t1​]
坐标系W到坐标系B的转换矩阵:
$$T_W^B=\left[\begin{array}{cc}{R}^T& -R^{T}t\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}{R}^{-1}& -R^{-1}t\\ 0& 1\end{array}\right]$$

世界坐标系到机器人坐标系的转换矩阵就是位姿

机器人A在坐标系W的坐标：
( x A , y A , θ A ) , [ c o s θ − s i n θ x A s i n θ c o s θ y A 0 0 1 ] (x_A, y_A, \theta_A),

$$\begin{bmatrix}cos\theta & -sin\theta & x_A \\ sin\theta & cos\theta & y_A \\ 0 & 0 & 1\end{bmatrix}$$ (xA​,yA​,θA​),⎣⎡​cosθsinθ0​−sinθcosθ0​xA​yA​1​⎦⎤​

机器人B在坐标系W中的坐标：
( x B , y B , z B ) , [ c o s θ − s i n θ x b s i n θ c o s θ y B 0 0 1 ] (x_B, y_B, z_B),

$$\begin{bmatrix}cos\theta & -sin\theta & x_b \\ sin\theta & cos\theta & y_B \\ 0 & 0 & 1 \end{bmatrix}$$ (xB​,yB​,zB​),⎣⎡​cosθsinθ0​−sinθcosθ0​xb​yB​1​⎦⎤​

机器人A在机器人B中的坐标：
$$T_A^B=T_W^B{T}_A^W={T_B^W}^{-1}{T}_A^W$$