第十三周：机器学习周报_chebnet模型

目录

摘要

Abstract

回顾

ChebNet

切比雪夫多项式(ChebShev Polynomial)

ChebNet公式推导

GCN（图卷积神经网络）

GCN公式推导

GCN原理

对比ChebNet与GCN

GCN的Pytorch实现

总结

---

摘要

上周学习了GNN的基于空间和谱域两种卷积方式，以及基于空间的模型，这周接着学习了基于谱域的两种模型：ChebNet和GCN，ChebNet采用切比雪夫多项式优化传统的基于谱域的卷积中处理复杂的特征分解的难题，大大减少计算量。而GCN又在ChebNet的基础上进一步简化，相当于一阶切比雪夫卷积的再近似。通过手写推导公式了解简化的原理，最后对两者进行对比，通过代码实例进一步了解GCN模型。

Abstract

Last week, we learned two GNN convolution methods based on spatial domain and spectral domain, as well as spatial-based models. This week, we continued to learn two GNN models based on spectral domain: ChebNet and GCN. ChebNet uses Chebyshev polynomials to optimize the complex Eigendecomposition of a matrix problem in traditional spectral domain based convolution, which greatly reduces the amount of computation. And GCN is further simplified on the basis of ChebNet, equivalent to a re approximation of first-order Chebyshev convolution. Understand the principle of simplification through handwritten derivation of formulas, and finally compare the two to further understand the GCN model through code examples.

回顾

最常用的几个神经网络经典模型CNN、RNN等，虽然它们在NLP、CV等领域都得到了很好的表现，但是在处理图结构的数据的时候，却没有好的解决方法，得不到好的表现。

对于CNN

CNN在做图像识别任务的时候，可以通过定义一个kernel在图片上进行平移做卷积的方式，提取图片的特征进行识别。对于二维的图片而已，kernel平移到每一个位置的内部结构都是不变的，这就是因为图片结构的的平移不变性，因此CNN可以实现参数共享。

对于RNN

RNN是专门处理一维结构的自然语言等序列信息，通过门结构，能够使得输入的前后信息之间相互影响，在考虑全局信息的情况下进行识别判断等任务。

而数据结构的图是一种不规则的无限维数据，例如化学分子组成、每一个节点的周围结构都是独一无二的，因此不具有平移不变性，CNN、RNN等方法在此问题上就失效了。

ChebNet

原始的基于频谱的图卷积中需要学习的参数数量与图的节点数量一样，因此卷积核过“大”，需要进行复杂特征分解，运算的复杂度高。为了解决复杂的计算，ChebNet采用Chebyshev（切比雪夫）多项式代替谱域的卷积核，即对参数化的频率响应函数进行多项式近似。

 其中k代表多项式的最高阶数，这一步近似将卷积核的参数数量从n个减少到了k个，使卷积核变“小”了，而不再是“全局”变得“局部”了。

但是，整个图卷积运算的复杂度还是O()，因为输入信号要与傅里叶基U做矩阵乘法。为了进一步降低计算复杂度，使用迭代定义的切比雪夫多项式(ChebShev Polynomial)作近似并证明可以将计算复杂度降低至O(KE)，其中K为多项式的阶数，E为图中边的数量。

切比雪夫多项式(ChebShev Polynomial)

ChebNet公式推导

运用切比雪夫多项式对原始的GCN频域建模算法进行改进

 那为什么要将多项式进行转换？对于下图中的例子而言，将多项式进行转换，换成的形式，找出前面的系数之后，带入1,99每一项就是0.01，这样计算f(1.99)的近似值的话就会变得很好算。因此切比雪夫多项式的这个模型做的事情就类似于这样，左边的就是多项式中的，就是前的系数，使用切比雪夫多项式的目的就是希望是很好算的，最后要学的东西就是。  

ChebNet结论：就是学习一个filter，而这个filter要做的事情就是要学习一组参数，先将输入的信号通过递回的方式计算到k次方，然后乘以一个weight matrix之后就可以得到filter完的信号。 （其中K为多项式的阶数，E为图中边的数量）

filter可以不止一个，是一组filter参数，因此可以学习一组参数，类似于CNN中可以有多个channel，第一组参数得到输出，第二组参数得到输出。
 

GCN（图卷积神经网络）

GCN实际上跟CNN的作用一样，就是一个特征提取器，只不过它的对象是图数据。GCN精妙地设计了一种从图数据中提取特征的方法，从而让我们可以使用这些特征去对图数据进行节点分类（node classification）、图分类（graph classification）、边预测（link prediction），还可以顺便得到图的嵌入表示（graph embedding）。初期研究者为了从数学上严谨的推导GCN公式是有效的，所以会涉及到诸如傅里叶变换，拉普拉斯算子的知识。其实对于我们使用者而言，我们可以绕开那些知识并且毫无影响的理解GCN。

相比于ChebNet而言，GCN的卷积核更小，参数量也更少，计算复杂度也随之变小了，可以说是将chebnet进行了简化，它等价于最简的一阶切比雪夫卷积。

GCN公式推导

​

假设有一个图数据，一共有N个节点（node），每个节点都有自己的特征，我们设这些节点的特征组成一个N×D维的矩阵X，然后各个节点之间的关系也会形成一个N×N维的矩阵A，也称为邻接矩阵（adjacency matrix）。X和A便是我们模型的输入。

​ 下图就是GCN网络层的基础公式，这个式子的意思就是，先把node feature（x)mm经过一个transform，把所有的邻居节点以及它自己本身加起来取平均值，再加一个b经过一个activation之后就会得到最后的。

​

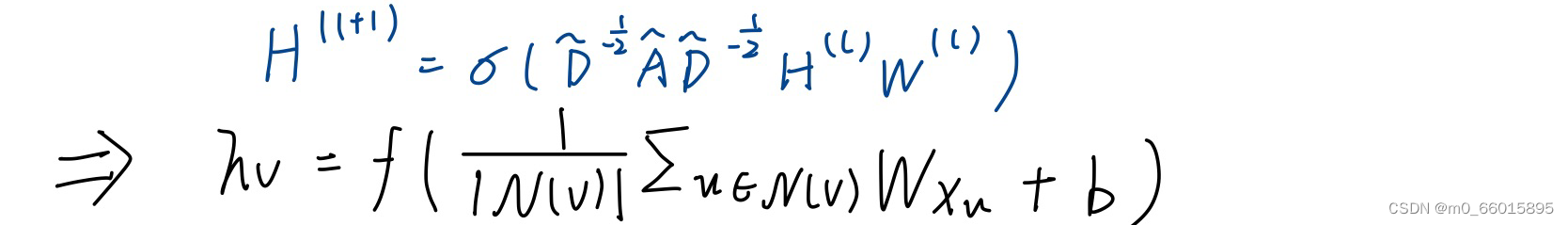
GCN原理

通过一个例子对公式原理进行分析

下一层某一节点的向量表示就是当前层节点向量表示的和，这其实是一个消息传递的过程，经这样消息传递的操作后，下一层的节点就聚集了它一阶邻居与自身的信息。这就很有效的保留了图结构给我们承载的信息。因此的含义即聚合周围节点的信息，来更新自己。

而简单的聚合却不太合理，因为不同的节点重要性不一样，如果一个节点的「度」非常大，即与他相邻的节点非常多，那么它传递的消息，权重就应该小一点。对于度矩阵D，其数值就是代表一个节点的邻居节点数量，所以乘以度矩阵的逆也就是稀释掉度很大的节点的重要度。

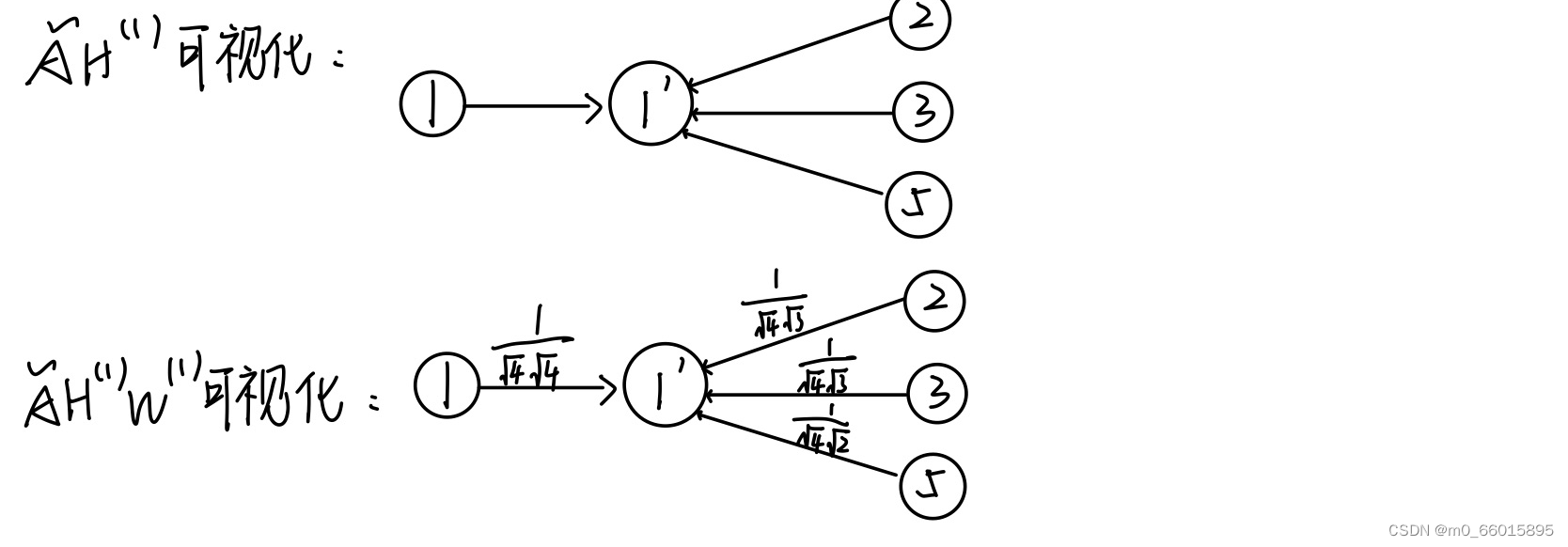
GCN也是一个神经网络层，这里的权重是所有节点共享的，类比于CNN中的参数共享；另外可以将节点的邻居节点看成感受野，随着网络层数的增加，感受野越来越大，即节点的特征融合了更多节点的信息。直观的图卷积示意图如下：：

​

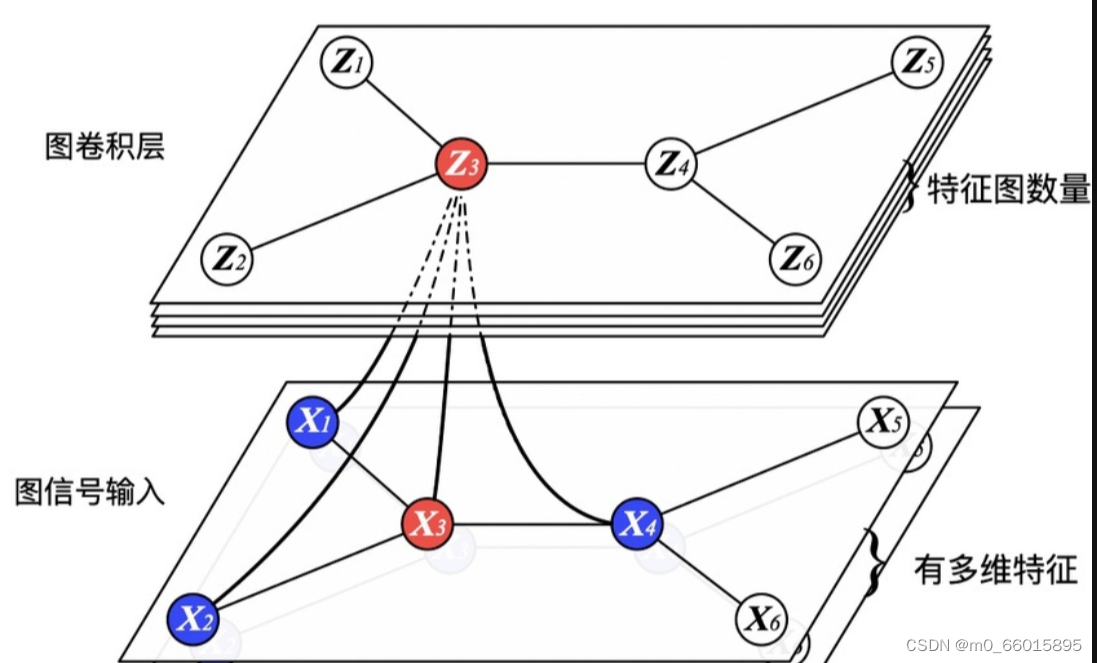
每一层GCN的输入都是邻接矩阵A和node的特征H，再乘一个参数矩阵W，然后激活一下，这就相当于一个简单的神经网络层，但是这种做法存在局限性。
一、输入神经网络的如果是矩阵A，矩阵A的对角线数值全为0，那么当矩阵A与特征矩阵H相乘，是会计算一个节点所有邻居的特征加权和，意味着该节点只考虑了邻居节点而没有将自身考虑进去，会疏忽了自身的特征，因此给邻接矩阵A加上一个单位矩阵I，将矩阵A的对角线数值都变成1。
二、邻接矩阵A的值是没有经过归一化的，在神经网络中经过多层堆叠与特征矩阵相乘会改变特征原本的分布，容易产生梯度爆炸、梯度消失等问题。所以需要对矩阵A做“归一化”处理。首先让A的每一行加起来为1，我们可以乘以一个D的逆，D就是度矩阵。我们可以进一步把D的拆开与A相乘，得到一个对称且归一化的矩阵 。

GCN的优点

1、即使不训练，使用随机初始化的参数W，GCN提取出来的特征十分优秀。

2、即使是节点没有很多特征，也可以使用GCN。可以用单位矩阵替换特征矩阵X。

3、即使节点没有任何的类别标准或者其他标准，也可以使用GCN。

对比ChebNet与GCN

一、GCN是ChebNet的简化版，ChebNet的复杂度和参数量比GCN要高，但是表达能力强。
二、ChebNet的K阶卷积可以覆盖节点的K阶邻居节点，而GCN则只覆盖一阶邻居节点，但是通过堆叠多个GCN层也可以扩大图卷积的感受域，所以灵活性比较高。
三、复杂度较低的GCN相比之前的方法都更加易于训练，速度快且效果好，实用性很强，所以成为了被最多提到的典型方法。

GCN的Pytorch实现

1、定义GCN卷积层

GCNConv的常用参数：

in_channels：每个样本的输入维度，就是每个节点的特征维度
out_channels：经过注意力机制后映射成的新的维度，就是经过GAT后每个节点的维度长度
add_self_loops：为图添加自环，是否考虑自身节点的信息
bias：训练一个偏置b

接下来就可以定义GCNConv层了，该层分别实现了reset_parameters() 、 get_L_sym()、forward()。

reset_parameters()：初始化可学习参数

get_L_sym()：矩阵归一化，计算GCN公式中，由于这部分不依赖数据，所以只需要计算一次，然后保留到类内部参数即可
forward()：这个函数定义模型的传播过程，也就是上面公式，如果设置了偏置在加上偏置返回即可

class GCNConv(nn.Module):
    def __init__(self, in_channels, out_channels, add_self_loops=True, bias=True):
        super(GCNConv, self).__init__()
        self.in_channels = in_channels # 输入图节点的特征数
        self.out_channels = out_channels # 输出图节点的特征数
        self.add_self_loops = add_self_loops # 是否考虑节点自身添加自环
        
        self.adj = None # 邻接矩阵A
        self.degree = None # 度矩阵D
        self.degree_2 = None # D^(-0.5)
        self.adj_t = None # D^(-0.5)AD^(-0.5)
        
        # 定义参数 θ
        self.weight = nn.Parameter(torch.FloatTensor(in_channels, out_channels))
        if bias:
            self.bias = nn.Parameter(torch.FloatTensor(out_channels, 1))
        self.init_parameters()
    
    # 初始化可学习参数
    def init_parameters(self):
        nn.init.xavier_uniform_(self.weight)
        if self.bias != None:
            nn.init.xavier_uniform_(self.bias)
            
    # 计算D^(-1/2)AD^(-1/2)
    def get_L_sym(self, x, edge_index):
        # 1.获取邻接矩阵A
        if self.adj == None:
            self.adj = coo_matrix(
                (torch.ones(edge_index.shape[1]), (edge_index[0].numpy(), edge_index[1].numpy())),
                shape=(x.shape[0], x.shape[0]))
 
            values = self.adj.data
            indices = np.vstack((self.adj.row, self.adj.col))
 
            i = torch.LongTensor(indices)
            v = torch.FloatTensor(values)
            shape = self.adj.shape
            self.adj = torch.sparse.FloatTensor(i, v, torch.Size(shape)).to_dense()
        
        # 2.添加自环
        if self.add_self_loops:
            self.adj = self.adj + torch.eye(self.adj.shape[0])
        
        # 3.获取度矩阵D
        if self.degree == None:
            self.degree = self.adj.sum(axis=1)
        
        # 4.获取D^(-0.5)
        if self.degree_2 == None:
            self.degree_2 = torch.torch.diag_embed(torch.pow(self.degree, -0.5).flatten())
        
        # 5.计算D^(-0.5)AD^(-0.5)
        if self.adj_t == None:
            self.adj_t = torch.mm(self.degree_2, self.adj).mm(self.degree_2)
        
    def forward(self, x, edge_index):
        # 1.获取D^(-0.5)AD^(-0.5)
        if self.adj_t == None:
            self.get_L_sym(x, edge_index)
            
        # 2.计算HW
        x = torch.mm(x, self.weight) # num_nodes, out_channels
        
        # 3.计算D^(-0.5)AD^(-0.5)HW
        output = torch.spmm(self.adj_t, x) # 计算
        
        # 4.添加偏置
        if self.bias != None:
            return output + self.bias.flatten()
        else:
            return output

2、定义GCN 网络

上面以及实现了GCN卷积的网络层，后面就可以调用这个层来搭建GCN网络。

# 定义GCN网络
class GCN(nn.Module):
    def __init__(self, num_node_features, num_classes):
        super(GCN, self).__init__()
        self.conv1 = GCNConv(num_node_features, 16)#定义GCN卷积网络层1
        self.conv2 = GCNConv(16, num_classes)#定义GCN卷积网络层2
        
    def forward(self, data):
        x, edge_index = data.x, data.edge_index#定义输入节点、边
        
        x = self.conv1(x, edge_index)
        x = F.relu(x)#计算通过激活函数ReLU
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)
        
        return F.log_softmax(x, dim=1)

上面网络我们定义了两个GCNConv层，第一层的参数的输入维度就是初始每个节点的特征维度，输出维度是16。第二个层的输入维度为16，输出维度即为分类个数。

总结

这周学习了基于谱域的卷积方式中的两个经典模型，其中GCN是Spectral-based GNN中用得最多的模型。ChebNet模型利用切比雪夫多项式的转换解决了传统基于谱域的卷积中存在的问题，比如参数与输入的图有关，每次输入都要重新学习参数，当图片过大时参数量就会很大，运算复杂度高，除此之外避免模型学到了“不想要”的东西。而GCN则是在ChebNet的基础上进一步简化，是ChebNet中k=1的情况，并解决了自身特征值被忽略的情况，以及将邻接矩阵进行改进，进行了归一化处理。