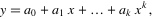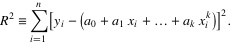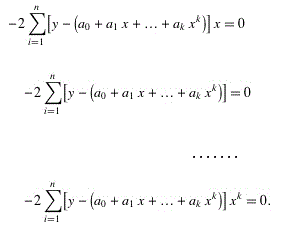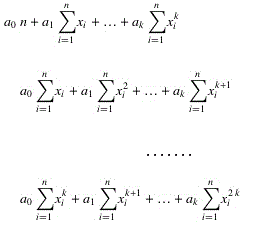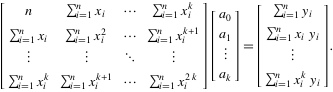热门标签
热门文章
- 1基于MATLAB深度学习工具箱的CNN卷积神经网络训练和测试_matlab卷积神经网络
- 2【无人机编队】二阶一致性多无人机协同编队控制(考虑通信半径和碰撞半径)【含Matlab源码 4215期】
- 3数学建模|前馈神经网络之模式识别基础(分类问题)_前馈神经网络处理分类问题的原理
- 4授权/非授权技术各擅专场 LPWAN群雄比拼物联网
- 5李沐动手学深度学习V2-多头注意力机制和代码实现_多头自注意力
- 6Google C++项目编程风格指南 (中文版) 分享
- 7Dockerfile安装到项目发布全过程(详解)_dockerfile镜像部署
- 8前沿 | 使用Transformers进行端到端目标识别
- 9Python 自然语言处理:使用 NLTK 库进行词性标注_python词性标注的库
- 10C++STL--排序算法
当前位置: article > 正文
算法#03--详解最小二乘法原理和代码_最小二乘法 高斯消元法
作者:AllinToyou | 2024-03-27 18:50:43
赞
踩
最小二乘法 高斯消元法
最小二乘法原理
最小二乘法的目标:求误差的最小平方和,对应有两种:线性和非线性。线性最小二乘的解是closed-form(如下文),而非线性最小二乘没有closed-form,通常用迭代法求解(如高斯牛顿迭代法,本文不作介绍)。
【首先得到线性方程组】
1.概念
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
2.原理
函数原型:
已知:
(x0,y0),(x1,y1)…(xi,yi)…(xn,yn)个点,n>=k。
偏差平方和:
偏差平方和最小值可以通过使偏导数等于零得到:
简化左边等式有:
写成矩阵形式:公式①
将这个范德蒙得矩阵化简后可得到:公式②
也就是说X*A=Y,那么A = (X’*X)-1*X’*Y,便得到了系数矩阵A,同时,我们也就得到了拟合曲线。
高斯消元法
【然后解线性方程组,即公式①】
1.概念
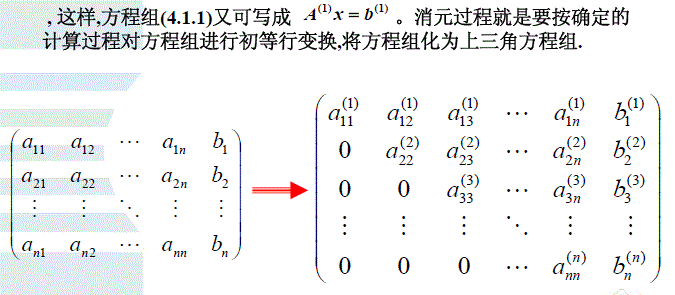
数学上,高斯消元法(或译:高斯消去法)(英语:Gaussian Elimination),是线性代数中的一个算法,可用来为线性方程组求解,求出矩阵的秩,以及求出可逆方阵的逆矩阵。当用于一个矩阵时,高斯消元法会产生出一个“行梯阵式”。
2.原理
3.伪代码
这个算法和上面谈到的有点不同,它由绝对值最大的部分开始做起,这样可以改善算法的稳定性。本算法由左至右地计算,每作出以下三个步骤,才跳到下一列和下一行:
- 定出i列的绝对值最大的一个非0的数,将第i行的值与该行交换,使得该行拥有该列的最大值;
- 将i列的数字除以该数,使得i列i行的数成为1;
- 第(i+1)行以下(包括第(j+1)行)所有元素都转化为0。
所有步骤完成后,这个矩阵会变成一个行梯矩阵,再用代入法就可以求解该方程组。
i = 1
j = 1
while (i ≤ m and j ≤ n) do
Find pivot in column j, starting in row i // 从第i行开始,找出第j列中的最大值(i、j值应保持不变)
maxi = i
for k = i+1 to<- 1
- 2
- 3
- 4
- 5
- 6
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/AllinToyou/article/detail/326305
推荐阅读
相关标签