AllinToyou

这个屌丝很懒，什么也没留下！

热门标签

结合openCV学习DIP之传统图像特征与匹配_cv::feature2d::compute

作者：AllinToyou | 2024-03-29 19:17:56

踩

cv::feature2d::compute

前言

关于图像的预处理部分参考结合opencv学习DIP

概述

该笔记主要是基于DIP理论➕openCV实现,学习该笔记首先要确保通读DIP理论,并由自己的话描述相关知识,并且掌握openCV中的相关算子

这里主要是基于VS2017/2019来实现openCV3.4.10版本的操作

图像处理分为传统图像处理和基于深度学习的图像处理,当某章某节涉及到深度学习时,我会在标题后追加(深度学习)以示区分.

图像特征

图像的浅层特征主要是颜色、纹理和形状

图像特征是指: 可以表达图像中对象的主要信息, 并且以此为依据可以从其他未知图像中检测出相似或相同的该对象A.

在特征提取上,传统的图像处理都是自行设计提取固定特征的算子,在深度学习上主要是利用CNN网络来广泛的提取图像的特征.

在本章中主要介绍的是传统图像处理的经典的特征描述和提取方法,例如Haar、LBP、SIFT、HOG和DPM特征,其中的DPM特征是传统DIP在特征提取领域的天花板.

对于图像特征而言, 要分三个部分考虑, 即: 特征检测, 特征描述,特征匹配

梯度与方向导数

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿此梯度的方向变化最快，变化率最大（为该梯度的模）

垂直于边缘的方向, 是梯度方向,就是变化率最大的方向, 就是图像变化最明显的方向

方向导数, 在函数定义域的内点，对某一方向求导得到的导数。一般为二元函数和三元函数的方向导数，方向导数可分为沿直线方向和沿曲线方向的方向导数。

公式理解:

openCV中关于图像特征

openCV中的图像特征通用接口

分为:关键点检测,描述子提取,关键点过滤,匹配方法,结果显示

关键点检测,描述子提取,特征匹配都有一个通用的抽象类, 根据各个的算法不同,openCV设计了各个衍生类.

在使用下述类时,应包含cv::feature2D或cv::xFeature2D库


#include <iostream>
#include "opencv2/core.hpp"
#ifdef HAVE_OPENCV_XFEATURES2D
#include "opencv2/highgui.hpp"
#include "opencv2/features2d.hpp"
#include "opencv2/xfeatures2d.hpp"

在图像特征中, 往往包含了3个部分: 特征检测, 特征描述子,特征提取

特征检测/提取: 通过关键点的定义,搜索图像并查找该图像中的所有关键点;

特征描述子:为发现的每个关键点计算一个特征描述子,也叫特征描述符;

特征匹配:将早准备好的关键点的描述子和现有图片的特征描述子进行比较,查看是否存在匹配项.

opencv对这三个部分进行了不同的处理, 但维持了一个原则就是:对于不同的特征算法, 尽可能的提供一个通用的界面,这样可以方便的进行差异性比较.

上述通用界面的实现就是一个抽象类, 其衍生类对应各种不同的算法

基于上述的思想, 先介绍描述关键点的实现类

cv::KeyPoint

关键点并不是特征描述子,对于关键点而言,一般情况下只在乎关键点所在的具体位置

cv::KeyPoint类是用来存储关键点信息的


cv::KeyPoint::KeyPoint( float x,  //关键点的位置
                        float 	y,
                        float 	_size,//关键点的周围区域信息
                        float 	_angle = -1,//角度
                        float 	_response = 0,//响应, 一般不使用
                        int 	_octave = 0, //金字塔组数
                        int 	_class_id = -1  //分类
)

cv::Feature2D

对于openCV3.x 之后, 为了找到关键点和计算特征描述子, 或者同时执行这两步, openCV提供一个通用的抽象类,对于任何特征相关的算法都可以使用其来进行关键点的寻找和描述子的计算,

算法的不同,抽象类的成员函数返回的关键点和描述子包含的信息自然是不同的

⚠️ 描述子一般是设置成单通道的, 其任何类似通道的元素都将被展平成描述子的整体长度


class cv::Feature2D : public cv::Alogrithm
{
public:
//单图
    virtual void detect(
            cv::InputArray image, 
            vector<cv::keyPoint> & keypoints,
            cv::InputArray mask=cv::noArray(), 
            )const;
 
//多图                
    virtual void detect(
            cv::InputArrayOfArrays images, 
            vector< vector<cv::keyPoint> > & keypoints,
            cv::InputArrayOfArrays  mask=cv::noArray(),
            )const;
 
//单图
    virtual void compute(
            cv::InputArray image, 
            vector<cv::keyPoint> & keypoints,
            cv::OutputArray descriptors,  //常用cv::Mat格式
            );
 
//多图
    virtual void compute(
            cv::InputArrayOfArrays image, 
            vector<vector<cv::keyPoint> >& keypoints,
            cv::OutputArrayOfArrays descriptors, //常用cv::Mat格式
            );
 
//关键点和描述子同时进行
    virtual void detectAndCompute(
            cv::InputArray image, 
            cv::InputArray mask,
            vector<cv::keyPoint> & keypoints,
            cv::OutputArray descriptors,    //常用cv::Mat格式
            bool useProvidedKeypoints = false, 
                    //true就使用keypoints,false就自动检测
            );
 
    virtual int descriptorSize() const; //返回描述子长度
//二进制描述子返回字节数, 通常则返回描述符矩阵的列
 
    virtual int descriptorType()const;    //返回描述子包含的元素类型
//如CV_32FC1, CV_8UC1等
 
    virtual int defaultNorm()const;    //返回描述子的比较方法
//二进制描述符用NORM_HAMMING, SIFT/SRUF用NORM_L2或NORM_L1
    
    virtual void read(const cv::FileNode&);    
    virtual void write(cv::FileStorage&)const;
 
    ...
 
};

上述是cv::Feature2D的部分类声明

对于单纯的关键点检测算法,如FAST,实现过程或许只需要用到cv::Feature2D::detect();

对于纯特征描述子算法,如FREAK, 实现过程或许只会用到cv::Feature2D::compute()

对于“完全解决”的算法,如SIFT,SURF,ORB,BRISK等,实现过程需要cv::Feature2D::detectAndCompute(),该接口比先detect()再compute()分开执行的性能要好很多, 主要是因为分开执行时需要计算两次尺度空间,而detectAndCompute()只计算一次.

cv::DMatch

上述完成了特征的检测和描述, 下一步就是特征的匹配,

匹配器的工作原理:

把一个图像的关键点,和另一个图像进行匹配, 找到匹配时,生成cv::DMatch对象的列表,用来描述匹配的结果

cv::DMatch对象仅仅是用来存储一个关键点匹配的结果的,类似KeyPoint类,

和KeyPoint类相似,一般只关注keypoint存储的点的位置, 而DMacth一般只关注描述子的索引值和质量值


class cv::DMatch
{
public:
    DMatch();
    
    DMatch( int _queryIdx,
            int _trainIdx,     
            float _distance);
    
    DMatch( int _queryIdx,
            int _trainIdx,
            int _imgIdx,
            float _distance);
 
    int queryIdx; //要匹配的描述子 在目标图像中的索引
    int trainIdx;    //描述子在训练图片中的索引
    int imgIdx;    //训练图片的索引
    float distance;    //匹配质量,常用欧氏距离表示,越小越好
 
    bool operator<(const DMatch&m)const;//小于号运算符重载,用来比较成员distance方便排序
};

深入理解DMatch的用法

在后续学习中,发现经常出现vector<DMatch> 或者vector<vector<DMatch>>

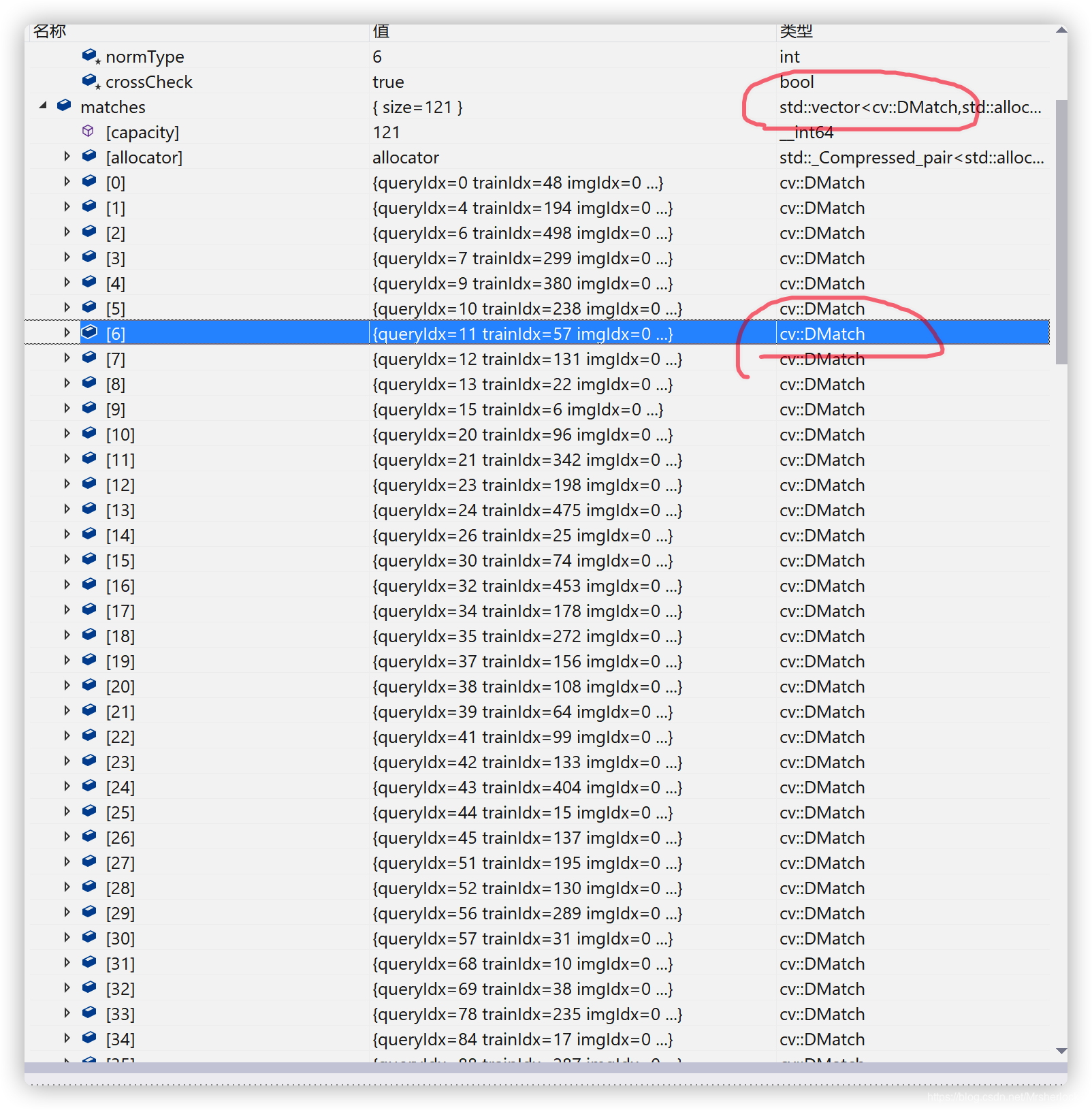
DMatch中到底存储了什么? 用一个测试结果图来展示, 即在vector<DMatch> matches 对象中,存了size=121个DMatch对象, 每个DMatch都包含了一个queryIdx和trainIdx(如上所述), 这里的意思是:

以[6]为例:

第六个匹配结果, 即目标图像的描述子列表中的第11个描述子,queryIdx=11, 和训练过的图片/原图片的描述子列表的第57个描述子, 这两个描述子包含的特征信息是一致的.(当然这里仅仅是基于某个匹配算法的结果,未必是绝对一致或绝对相同,需要后续筛选)

由于描述子中不仅包含了图像特征信息还包含了对应关键点的坐标,因此可以根据该匹配结果列表即vector<DMatch> matches 和两张图的关键点对象,来绘制出两个描述子在对应图片的两个位置之间的连线

cv::DescriptorMatcher

DescriptorMatcher类作为一个抽象类,类似Feature2D, 根据匹配的算法不同,有衍生了很多不同的类

对于图像的特征检测设计了很多不同的算法,对于描述子的匹配同样也设计了很多不同的算法.

从使用场景来说:

用于对目标进行匹配,一般需要用到匹配的场景有两种:目标识别和跟踪

目标识别: 首先将各种对象关联的关键点编译成数据库,称为“字典”, 出现新场景时,提取目标图像中的关键点,生成关键点列表,然后查询已训练过的字典进行比较,用来估计目标图像中,存在“字典”所包含的对象的可能性,即匹配程度.

综上所属该场景下的匹配器需要输入:

1. 需要包含相关描述子的字典, 且字典已完成训练

2. 从目标图像中提取一个特征列表

跟踪:通常和视频流相关,一般是对相邻两帧,进行关键点比较,即查询第 i 帧的全部关键点,再查找第i+1 帧中全部的关键点,进行比较.

1.从上下两帧目标图像中,分别提取两个特征列表

2. 匹配器返回我们两个列表之间的匹配位置

综上所述:

目标识别场景,需要: 目标图像的一个特征列表+经训练过的字典

跟踪场景:需要: 上下两帧目标图像对应的两个特征列表

cv::DescriptorMatcher类提供了3个函数,match(), knnMatch(), radiusMatch() ,每个函数都针对上述两个场景做了两个变形,即共6个函数,


//详细描述见下文
class cv::DescripatorMatcher
{
public:
    virtual void 	add (InputArrayOfArrays descriptors); //
    virtual void 	clear ();
    virtual bool    empty()const; //判断对象是否关联了描述子
    void train();
    virtual bool    isMaskSupported() cosnt = 0;
    const vector<cv::Mat>    & getTrainDescriptors() const;
 
//recognition
 
    void match(
        InputArray queryDescriptors,
        vector<cv::DMatch>& matches,
        InputArrayOfArrays masks = noArray());
 
    void knnMatch(
        InputArray queryDescriptors,
        vector< vector<cv::DMatch> >& matches,
        int k,
        InputArrayOfArrays masks = noArray(),
        bool compactResult = false);
        
    void radiusMatch(
        InputArray queryDescriptors,
        vector <vector<cv::DMatch> >& matches,
        float maxDistance,
        InputArrayOfArrays masks = noArray(),
        bool compactResult = false);
                      
//tracking
    void match(
        InputArray queryDescriptors,
        InputArray trainDescriptors,
        vector <cv::DMatch>& matches,    
        InputArray mask = noArray())const;    
 
    void knnMatch(
        InputArray queryDescriptors,
        InputArray trainDescriptors,
        vector< vector<cv::DMatch>>& matches,
        int k,
        InputArray mask = noArray(),
        bool compactResult = false)const;
 
    void radiuMatch(
        InputArray queryDescriptors,
        InputArray trainDescriptors,
        vector< vector<cv::DMatch>& matches,
        float maxDistance,    
        InputArray mask = noArray(),
        bool compactResult = false)const;
 
 
    virtual void read(const FileNode&);
    virtual void write(FileStorage&)const;
    virtual cv::Ptr<cv::DescriptorMatcher> clone(
            bool emptyTrainData = false;)const = 0;
    static cv::Ptr<cv::DescriptorMatcher> create(
            const string& descriptorMatcherType);
...
};

在该类的前部,定义了几个通用的方法,这些方法用于新图像和预先存储的描述子集合匹配, 每个图像一个阵列,目的是建立一个关键点字典,在提供新的关键点时查询字典进行匹配.

add()

用于添加描述子列表, 每一个描述子都是cv::Mat对象,每个Mat对象都有N行 D列,每一行表示一个描述子, 即:行表示描述符的数量,列表示描述符的维度

要添加的描述符。每个描述符 [i] 是来自同一训练图像的一组描述符。

virtual void 	add (InputArrayOfArrays descriptors);

clear()

清空当前对象关联的描述子

virtual void 	clear ();

train()

DescriptorMatcher的一些派生类会用到train()方法, 一般对目标图片的特征列表和字典进行欧氏距离计算时,需要生成一些数据结构,然后执行匹配算法, 这在匹配时需要消耗时间, train()是告诉匹配器在执行匹配算法前,提前生成相关的数据结构,即预处理信息.

该方法的目的是,告诉匹配器可以进行处理预计算的信息了, 从而为新关键点的匹配准备

void train();

目标识别相关的接口

在目标识别中使用的一组匹配方法。它们每个都使用描述符列表，称为查询列表，并与训练好的字典中的描述符进行比较。这些方法中的每一种以稍微不同的方式计算匹配。
match()


void match(
        InputArray queryDescriptors, // 输入秒表图片Mat关键点描述符
        vector<cv::DMatch>& matches,    //输出匹配的结果DMatch对象
        InputArrayOfArrays masks = noArray());

该方法需要通常的cv::Mat格式的单个关键点描述符列表queryDescriptors。在这种情况下，请记住Mat对象的每行代表单个描述符，每列是该描述符向量表示的一个维度。

match()还需要一个cV::DMatch对象的vector向量，它可以填充各个检测到的匹配项。

        在match()方法的情况下，查询列表上的每个关键点将与列表中的“最佳匹配”匹配。
        match()方法也支持可选的mask参数。与OpenCV中的大多数mask参数不同，该掩码不在像素空间中操作，而是在描述符的空间中。然而，mask的类型应该仍然是CV_8U。mask参数是cv::Mat对象的STL向量即std::vector<cv::Mat>。该向量中的每个矩阵对应于字典中的训练图像之一.
        特定掩码中的每一行对应于queryDescriptors中的一行（即一个描述符）。掩码中的每个列对应于与字典图像相关联的一个描述符。因此，如果来自图像（对象）k的描述符j与查询图像中的描述符i进行比较，则masks［k］.at＜uchar＞（i，j）应该是非零的。

knnMatch()


//k-最近邻算法
void knnMatch(
        InputArray queryDescriptors,//目标图片的特征描述子Mat
        vector< vector<cv::DMatch> >& matches, //输出的DMatch结果
        int k,        //在字典中找个k个最佳匹配
        InputArrayOfArrays masks = noArray(),
        bool compactResult = false);

它需要与match()相同的列表描述符。

然而，在这种情况下，对于查询列表中的每个描述符，它将从字典中找到特定数量的最佳匹配。该数由整型参数k指定。

函数名中的“knn”代表k-最近邻。来自match()的cv::DMatch对象被替代成在knnMatch()方法中称为matches的cv::DMatch对象向量的向量。

顶级向量的每个元素（例如，matches［i］）都与queryDescriptors中的一个描述符相关联。对于每个这样的元素，下一级元素（例如，matches［i］［j］）是trainDescriptors中描述符的第j个最佳匹配。注18knnMatch（）的掩码参数与match（）的含义相同。

knnMatch（）的最后一个参数是布尔值compactResult。如果compactResult设置为默认值为false，则向量的匹配向量将包含一个向量条目，用于queryDescriptors中的每个条目－哪怕是那些没有匹配的条目（cv::DMatch对象的相应向量为空）。但是，如果将compactResult设置为true，那么这种非信息条目将简单地从匹配中移除。
radiusMatch()


void radiusMatch(
        InputArray queryDescriptors,
        vector <vector<cv::DMatch> >& matches,
        float maxDistance,//描述子最大直径距离
        InputArrayOfArrays masks = noArray(),
        bool compactResult = false);

与搜索k个最佳匹配的k-最近邻匹配不同，半径匹配返回了查询描述符特定距离内的所有匹配。
除了整数k代替最大距离maxDistance之外，参数及radiusMatch（）的均值都与knnMatch（）的相同。

跟踪相关的接口


//tracking
    void match(
        InputArray queryDescriptors,
        InputArray trainDescriptors,
//虽然叫train,但这只是第2个图片中提取到的特征列表
//不需要通过add()添加“训练”特征描述子列表
        vector <cv::DMatch>& matches,    
        InputArray mask = noArray())const;    
 
    void knnMatch(
        InputArray queryDescriptors,
        InputArray trainDescriptors,
        vector< vector<cv::DMatch>>& matches,
        int k,
        InputArray mask = noArray(),
        bool compactResult = false)const;
 
    void radiuMatch(
        InputArray queryDescriptors,
        InputArray trainDescriptors,
        vector< vector<cv::DMatch>& matches,
        float maxDistance,    
        InputArray mask = noArray(),
        bool compactResult = false)const;

其他接口

在了解完这六种匹配方法之后，还需要了解一些处理匹配器对象的方法。


    virtual void read(const FileNode&);
    virtual void write(FileStorage&)const;
    virtual cv::Ptr<cv::DescriptorMatcher> clone(
            bool emptyTrainData = false;)const = 0;
    static cv::Ptr<cv::DescriptorMatcher> create(
            const string& descriptorMatcherType);

read()和write()方法分别对应cV::FileNode和cv::FileStorage格式的对象，并允许你从磁盘读取和写入匹配器。尤其重要的是，当处理识别问题时，你可以通过从可能非常大的文件数据库加载信息来“训练”匹配器。这样可以节省你在每次运行代码时都需要加载实际的图像，并从每个图像重构关键点及其描述符。

clone()和create()方法允许你分别创建一个描述符的副本或者通过名称创建一个新的描述符。第一种方法clone()采用一个布尔值emptyTrainData，如果为true，它将创建具有相同参数值的副本（被特定匹配器接受的任何参数），但不复制内部字典。将emptyTrainData设置为false本质上是一个深层副本，它除了参数之外还复制字典。create（）方法是一个静态方法，它将接受可以构造特定派生类的单个字符串。

create()的descriptorMatcherType参数的当前可用值在表16-1中给出。

任何检测器找到的关键点都是有意义的,可以使用任何特征提取器来表征这些关键点

每个描述符类型,都有一个检测器和提取器, 检测器是完成关键点定位的任务, 提取器是对关键点计算特征描述符,即描述符提取器

案例:


#include <iostream>
#include "opencv2/core.hpp"
#ifdef HAVE_OPENCV_XFEATURES2D
#include "opencv2/highgui.hpp"
#include "opencv2/features2d.hpp"
#include "opencv2/xfeatures2d.hpp"
using namespace cv;
using namespace cv::xfeatures2d;
using std::cout;
using std::endl;
const char* keys =
    "{ help h |                  | Print help message. }"
    "{ input1 | box.png          | Path to input image 1. }"
    "{ input2 | box_in_scene.png | Path to input image 2. }";
int main( int argc, char* argv[] )
{
    CommandLineParser parser( argc, argv, keys );
    Mat img1 = imread( samples::findFile( parser.get<String>("input1") ), IMREAD_GRAYSCALE );
    Mat img2 = imread( samples::findFile( parser.get<String>("input2") ), IMREAD_GRAYSCALE );
    if ( img1.empty() || img2.empty() )
    {
        cout << "Could not open or find the image!\n" << endl;
        parser.printMessage();
        return -1;
    }
    //-- Step 1: Detect the keypoints using SURF Detector, compute the descriptors
    int minHessian = 400;
    Ptr<SURF> detector = SURF::create( minHessian );
    std::vector<KeyPoint> keypoints1, keypoints2;
    Mat descriptors1, descriptors2;
    detector->detectAndCompute( img1, noArray(), keypoints1, descriptors1 );
    detector->detectAndCompute( img2, noArray(), keypoints2, descriptors2 );
    //-- Step 2: Matching descriptor vectors with a brute force matcher
    // Since SURF is a floating-point descriptor NORM_L2 is used
    Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create(DescriptorMatcher::BRUTEFORCE);
    std::vector< DMatch > matches;
    matcher->match( descriptors1, descriptors2, matches );
    //-- Draw matches
    Mat img_matches;
    drawMatches( img1, keypoints1, img2, keypoints2, matches, img_matches );
    //-- Show detected matches
    imshow("Matches", img_matches );
    waitKey();
    return 0;
}
#else
int main()
{
    std::cout << "This tutorial code needs the xfeatures2d contrib module to be run." << std::endl;
    return 0;
}
#endif

结果

案例:Feature Matching with FLANN


#include <iostream>
#include "opencv2/core.hpp"
#ifdef HAVE_OPENCV_XFEATURES2D
#include "opencv2/highgui.hpp"
#include "opencv2/features2d.hpp"
#include "opencv2/xfeatures2d.hpp"
using namespace cv;
using namespace cv::xfeatures2d;
using std::cout;
using std::endl;
const char* keys =
    "{ help h |                  | Print help message. }"
    "{ input1 | box.png          | Path to input image 1. }"
    "{ input2 | box_in_scene.png | Path to input image 2. }";
int main( int argc, char* argv[] )
{
    CommandLineParser parser( argc, argv, keys );
    Mat img1 = imread( samples::findFile( parser.get<String>("input1") ), IMREAD_GRAYSCALE );
    Mat img2 = imread( samples::findFile( parser.get<String>("input2") ), IMREAD_GRAYSCALE );
    if ( img1.empty() || img2.empty() )
    {
        cout << "Could not open or find the image!\n" << endl;
        parser.printMessage();
        return -1;
    }
    //-- Step 1: Detect the keypoints using SURF Detector, compute the descriptors
    int minHessian = 400;
    Ptr<SURF> detector = SURF::create( minHessian );
    std::vector<KeyPoint> keypoints1, keypoints2;
    Mat descriptors1, descriptors2;
    detector->detectAndCompute( img1, noArray(), keypoints1, descriptors1 );
    detector->detectAndCompute( img2, noArray(), keypoints2, descriptors2 );
    //-- Step 2: Matching descriptor vectors with a FLANN based matcher
    // Since SURF is a floating-point descriptor NORM_L2 is used
    Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create(DescriptorMatcher::FLANNBASED);
    std::vector< std::vector<DMatch> > knn_matches;
    matcher->knnMatch( descriptors1, descriptors2, knn_matches, 2 );
    //-- Filter matches using the Lowe's ratio test
    const float ratio_thresh = 0.7f;
    std::vector<DMatch> good_matches;
    for (size_t i = 0; i < knn_matches.size(); i++)
    {
        if (knn_matches[i][0].distance < ratio_thresh * knn_matches[i][1].distance)
        {
            good_matches.push_back(knn_matches[i][0]);
        }
    }
    //-- Draw matches
    Mat img_matches;
    drawMatches( img1, keypoints1, img2, keypoints2, good_matches, img_matches, Scalar::all(-1),
                 Scalar::all(-1), std::vector<char>(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS );
    //-- Show detected matches
    imshow("Good Matches", img_matches );
    waitKey();
    return 0;
}
#else
int main()
{
    std::cout << "This tutorial code needs the xfeatures2d contrib module to be run." << std::endl;
    return 0;
}
#endif

关键点过滤

关键点个数太多时,需要进行过滤.使用cv::KeyPointsFilter类完成

你可能首先注意到的是所有这些方法都是static，所以真正的cv::KeyPointsFilter比一个对象更像一个命名空间。

五个滤波器方法中的每一个都引用了一个称为keypoints的cv::KeyPoint对象的STL样式向量。这是函数的输入和输出（即，你将给出关键点的函数，当你检查时，你会发现其中一些已经少了）。
cv::KeyPointsFilter::runByImageBorder()函数删除图像边缘的borderSize内的所有keypoints。你还必须通过imageSize参数告诉cv::KeyPointsFilter::runByImageBorder()一开始图像是多大。
cv::KeyPointsFilter::runByKeypointSize()函数将删除所有小于minSize或大于 maxSize的keypoints。cv::KeyPointsFilter::runBypixelsMask()函数删除与掩码中的零值像素相关联的所有 keypoints。
cv::KeyPointsFilter::removeDuplicated()函数删除所有重复的keypoints。
cv::KeyPointsFilter::retainBest()函数移除keypoints，直到达到由npoint给出的目标数字。关键点按其质量的升序排列，如response所示。


class CV_EXPORTS KeyPointsFilter
{
public:
    KeyPointsFilter(){}
 
    /*
     * Remove keypoints within borderPixels of an image edge.
     */
    static void runByImageBorder( std::vector<KeyPoint>& keypoints, Size imageSize, int borderSize );
    /*
     * Remove keypoints of sizes out of range.
     */
    static void runByKeypointSize( std::vector<KeyPoint>& keypoints, float minSize,
                                   float maxSize=FLT_MAX );
    /*
     * Remove keypoints from some image by mask for pixels of this image.
     */
    static void runByPixelsMask( std::vector<KeyPoint>& keypoints, const Mat& mask );
    /*
     * Remove duplicated keypoints.
     */
    static void removeDuplicated( std::vector<KeyPoint>& keypoints );
    /*
     * Remove duplicated keypoints and sort the remaining keypoints
     */
    static void removeDuplicatedSorted( std::vector<KeyPoint>& keypoints );
 
    /*
     * Retain the specified number of the best keypoints (according to the response)
     */
    static void retainBest( std::vector<KeyPoint>& keypoints, int npoints );
};

匹配方法

匹配方法主要有暴力匹配cv::BFMatcher和快速近邻匹配cv::FLannBasedMatcher,同样都是通过类对象调用成员函数来实现的

暴力匹配cv::BFMatcher

暴力匹配器基本上实现了匹配问题最直接的解决方案。它需要查询集里面的每个描述符，并尝试将其与训练集中的每个描述符（内部字典或查询集一起提供的集合）进行匹配。创建暴力匹配器时，只需要决定使用什么距离度量计算距离进行比较。

暴力匹配对象的最后一个特征是所谓的交叉检查（cross-checking）。参数cross-checking打开对cv::BFMatcher构造函数的交叉检查。当启用交叉检查时，仅当train［j］是训练集中的query［i］最接近的邻域并且query［i］是查询集中的train［j］最接近的邻域时才会报告查询集合的对象i与训练集合的对象j之间的匹配。这对于消除假匹配非常有用，但是会花额外的时间来计算。


class CV_EXPORTS_W BFMatcher : public DescriptorMatcher
{
public:
 
    CV_WRAP BFMatcher( int normType=NORM_L2, bool crossCheck=false );
 
    virtual ~BFMatcher() {}
 
    virtual bool isMaskSupported() const CV_OVERRIDE { return true; }
 
 
    CV_WRAP static Ptr<BFMatcher> create( int normType=NORM_L2, bool crossCheck=false ) ;
 
    virtual Ptr<DescriptorMatcher> clone( bool emptyTrainData=false ) const CV_OVERRIDE;
protected:
    virtual void knnMatchImpl( InputArray queryDescriptors, std::vector<std::vector<DMatch> >& matches, int k,
        InputArrayOfArrays masks=noArray(), bool compactResult=false ) CV_OVERRIDE;
    virtual void radiusMatchImpl( InputArray queryDescriptors, std::vector<std::vector<DMatch> >& matches, float maxDistance,
        InputArrayOfArrays masks=noArray(), bool compactResult=false ) CV_OVERRIDE;
 
    int normType;
    bool crossCheck;
};

@brief Brute-force matcher create method.

@param normType One of NORM_L1, NORM_L2, NORM_HAMMING, NORM_HAMMING2. L1 and L2 norms are

preferable choices for SIFT and SURF descriptors, NORM_HAMMING should be used with ORB, BRISK and

BRIEF, NORM_HAMMING2 should be used with ORB when WTA_K==3 or 4 (see ORB::ORB constructor

description).

@param crossCheck If it is false, this is will be default BFMatcher behaviour when it finds the k

nearest neighbors for each query descriptor. If crossCheck==true, then the knnMatch() method with

k=1 will only return pairs (i,j) such that for i-th query descriptor the j-th descriptor in the

matcher's collection is the nearest and vice versa, i.e. the BFMatcher will only return consistent

pairs. Such technique usually produces best results with minimal number of outliers when there are

enough matches. This is alternative to the ratio test, used by D. Lowe in SIFT paper.

快速近邻匹配cv::FLannBasedMatcher

术语FLANN是用于近似近邻计算的快速库FLANN的接口是通过cv::FlannBasedMatcher实现的,它继承于cv::DescriptorMatcher


class CV_EXPORTS_W FlannBasedMatcher : public DescriptorMatcher
{
public:
    CV_WRAP FlannBasedMatcher( const Ptr<flann::IndexParams>& indexParams=makePtr<flann::KDTreeIndexParams>(),
                       const Ptr<flann::SearchParams>& searchParams=makePtr<flann::SearchParams>() );
 
    virtual void add( InputArrayOfArrays descriptors ) CV_OVERRIDE;
    virtual void clear() CV_OVERRIDE;
 
    // Reads matcher object from a file node
    virtual void read( const FileNode& ) CV_OVERRIDE;
    // Writes matcher object to a file storage
    virtual void write( FileStorage& ) const CV_OVERRIDE;
 
    virtual void train() CV_OVERRIDE;
    virtual bool isMaskSupported() const CV_OVERRIDE;
 
    CV_WRAP static Ptr<FlannBasedMatcher> create();
 
    virtual Ptr<DescriptorMatcher> clone( bool emptyTrainData=false ) const CV_OVERRIDE;
protected:
    static void convertToDMatches( const DescriptorCollection& descriptors,
                                   const Mat& indices, const Mat& distances,
                                   std::vector<std::vector<DMatch> >& matches );
 
    virtual void knnMatchImpl( InputArray queryDescriptors, std::vector<std::vector<DMatch> >& matches, int k,
        InputArrayOfArrays masks=noArray(), bool compactResult=false ) CV_OVERRIDE;
    virtual void radiusMatchImpl( InputArray queryDescriptors, std::vector<std::vector<DMatch> >& matches, float maxDistance,
        InputArrayOfArrays masks=noArray(), bool compactResult=false ) CV_OVERRIDE;
 
    Ptr<flann::IndexParams> indexParams;
    Ptr<flann::SearchParams> searchParams;
    Ptr<flann::Index> flannIndex;
 
    DescriptorCollection mergedDescriptors;
    int addedDescCount;
};
 
#endif

结果显示

计算所有这些特征类型并计算从一个图像到另一个图像的匹配。

接下来要做的事情是在屏幕上实际显示关键点和匹配项。

OpenCV为这些任务提供了一个函数。
使用cv::drawKeypoints来显示关键点


 
void cv::drawKeypoints	(
	
    InputArray 	image,
    const std::vector< KeyPoint > & 	keypoints,
    InputOutputArray 	outImage,
    const Scalar & 	color = Scalar::all(-1),
    DrawMatchesFlags 	flags = DrawMatchesFlags::DEFAULT 
)

给定一个图像image和一组关键点keyPoints，cv::drawKeypoints()将把所有关键点标注到图像上并在outImg中输出结果。

注释的颜色可以用color设置，当设置为特殊值cV::Scalar::all(-1)时，表示它们应当使用不同的颜色。

flags参数可以设置为 cv:DrawMatchesFlags::DEFAULT或cv::DrawMatchesFlags::DRAW_RICH_KEYPOINTS。在前一种情况下，关键点用小圆标注。在后一种情况中，它们将用半径等于其size（如可获得）以及方位线由其angle（如可获得）给出的的圆圈来标注。

显示使用cv::drawMatches的关键点匹配


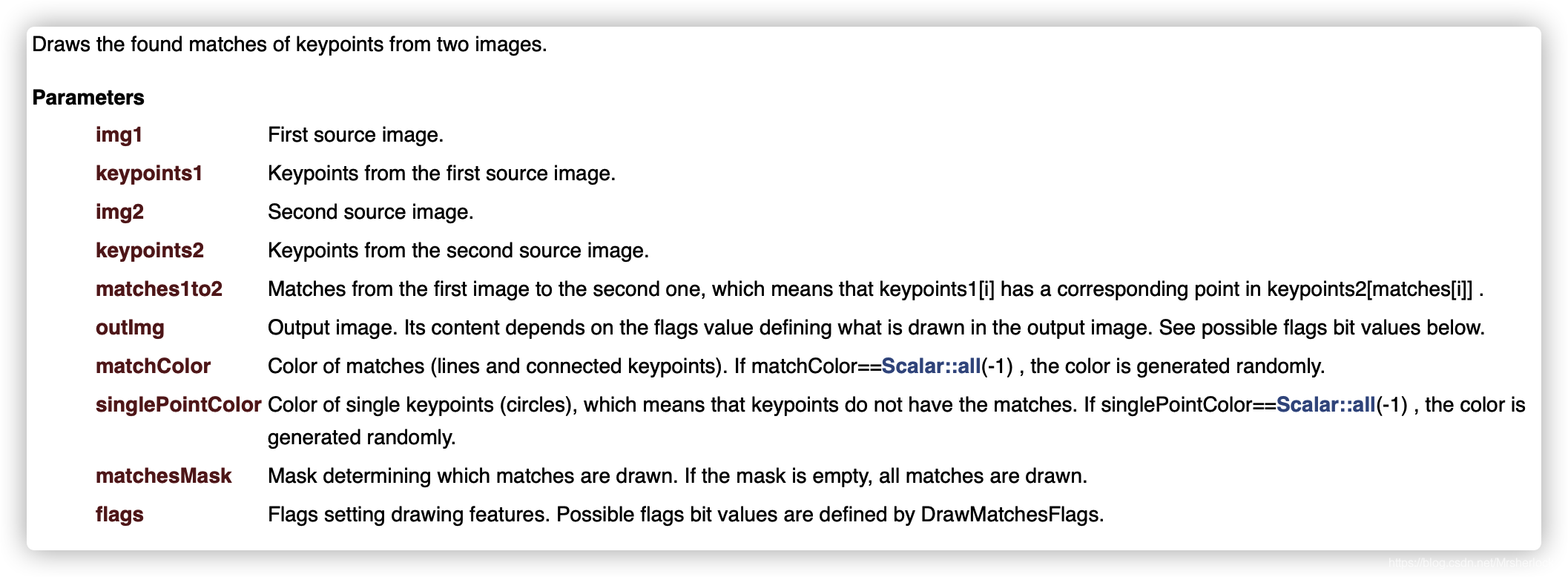
void cv::drawMatches	(	
        InputArray 	img1,
        const std::vector< KeyPoint > & 	keypoints1,
        InputArray 	img2,
        const std::vector< KeyPoint > & 	keypoints2,
        const std::vector< DMatch > & 	matches1to2,
        InputOutputArray 	outImg,
        const Scalar & 	matchColor = Scalar::all(-1),
        const Scalar & 	singlePointColor = Scalar::all(-1),
        const std::vector< char > & 	matchesMask = std::vector< char >(),
        DrawMatchesFlags 	flags = DrawMatchesFlags::DEFAULT 
)

给定一对图像、相关联的关键点以及一个由其中一个匹配器生成的cv::DMatch 对象列
表，cv::drawMatches()将会生成一幅图像，其中包含两个输入图像及所有关键点（以
cv::drawKeypoints()的样式），并指明第一个图像中的哪些关键点与第二个图像中的关
键点匹配。

cv::drawMatches()有两种变化形式；除了两个参数外，其余部分都相同。

openCV与Harris,Shi-Tomasi

根据上述原理,许多可追踪的特征才被称为角点,直观上看角点是从一帧到下一帧之间包含了足够多信息的点,并不是边缘的点.

cv::goodFeaturesToTrack()实现了Harris角点检测方法,该函数计算必要的导数,分析后返回符合我们定义的适合跟踪的点的列表;


void cv::goodFeaturesToTrack(
    cv::InputArray image, //输入图像8,32位单通道
    cv::OutputArray corners,//输出角点,vector或Mat
    int maxCorners,//包含的最多角点个数
    double qualityLevel,//角点质量,通常在0.01-0.1不能超过1.0
    double minDistance,    //相邻角点的最小间距
    cv::InputArray mask = noArray(),//和图片尺寸相同,
//角点不会在mask为0的地方生成
    int blockSize = 3,     //计算角点时考虑的区域大小
    bool useHarrisDetector = false,   
//算法选择,false使用Shi-Tomasi算法,tru使用Harris原始算法
    double k = 0.04); //只用于Harris算法,常不修改

openCV与亚像素角点

使用cv::cornerSubPix()来寻找亚像素角点,应注意: 输入是原始图像, 和cv::goodFeaturesToTrack()得到的角点像素位置


void cv::cornerSubPix(
    cv::InputArray image,    //原始图像
    cv::InputOutputArray corners,    
//input outputArray 输入cv::goodFeaturesToTrack()的角点列表
    cv::Size winSize,    
    cv::Size zeroZone,    
    cv::TermCriteria critertia
);

参数image:

输入image是计算角点的原始图像。

参数corners:

数组包含整数形式的像素位置，例如从例程cv：：goodFeaturesToTrack（）获取的像素位置，它们被设为角点位置的初始值。

亚像素位置的实际计算使用了点积表达式的系统，该系统表示一个和为零的组合.其中每个等式都考虑了p的周围区域的像素。

参数winSize:

指定将生成这些方程的窗口的大小。该窗口以整数形式的原始角点位置为中心，并在每个方向向外扩展，扩展距离为通过winSize指定的像素数，

例如，如果winSize．width＝ 4，则搜索区域实际上为4＋1＋4＝9像素宽。这些方程形成一个可以通过一个自相关矩阵的逆求解的线性系统。

在实践中，由于从非常接近p的像素产生的小特征值，该矩阵并不总是可逆的。为了防止这种情况，通常只考虑在p附近的像素。

参数zeroZone:

定义了一个窗口（类似于winSize，但范围较小），这在约束方程系统中将不被考虑，因此也就不再考虑自相关矩阵。如果不需要这样的零区域，则该参数应设置为cv::Size(-1,-1)

参数criteria:
一旦为q找到一个新的位置，算法将使用该值作为起始点进行迭代，并直到达到用户指定的终止标准。这个标准可以是cv::TermCriteria::MAX＿ITER类型或cv::TermCriteria::EPS类型（或两者）使用cv::TermCriteria::EPS将有效表示你需要的亚像素值的准确性。因此，如果指定0.10，则要求亚像素精度在像素的1／10以内。

通常用cv::TermCriteria()函数构造。

cv::GFTTDetector

对于Shi-Tomasi检测,默认情况下,opencv使用cv::GFTTDetector实现

关键点检测器Harris-Shi-Tomasi角点检测器

GFTTDetector检测器,通过crate()设置检测器属性,再通过调用父类的detect()接口,完成对图像的角点检测,如下:


class cv::GFTTDetector:public cv::Feature2D{
 
public:
    static Ptr<GFTTDetector> create(
        int maxConrners = 1000,  //最大角点个数
        double qualityLevel = 0.01, //最小低阶特征值,一般0.01-0.1,不超过1.0
        double minDistance = 1, //相邻角点的像素距离,即两点之间的像素数量
        int blockSize = 3,    //见上述的winSize
        bool useHarrisDetector = false, 
// true使用Harris原始算法, false使用Shi-Tomasi算法
        double k = 0.04 
//权重系数,用于在给定自相关矩阵Hessian的trace情况下,与该矩阵行列式比较时的权重
    );
...
};
 
 
Ptr<GFTTDetector> ptr; //表示GFTTDetector* ptr;
 
 
//e.g.
std::vector<cv::KeyPoint> key_points;
cv::Ptr<cv::GFTTDetector> gftt = cv::GFTTDetector::create(1000, .3, 5., 3, false);
gftt->detect(img, key_points);

openCV和SIFT

在openCV中的cv::Feature2D接口实现了SIFT算法的特征检测和描述子提取部分.

cv::xfeatures2d::SIFT

创建一个SIFT对象,使用其继承的cv::Feature2D::detectAndCompute()方法完成关键点检测和特征描述子计算提取.

使用SIFT的create()接口,完成对算法参数的设置.

SIFT算法在opencv_contrib/xfeatures2d模块中


class SIFT :public Feature2D
{
public:
    static Ptr<SIFT> create (
        int nfeatures = 0,    //图片中包含的最大特征数
        int nOctaveLayers = 3,    
//尺度空间中每组OCtave中层数,即高斯模糊系数个数
 
//设置阈值,确定是否保留已找到的候选关键点
        double contrastThreshold = 0.04,
//局部极值是否和周围区域完全不同
 
        double edgeThreshold = 10,
//空间特征值的比例相关,用于滤出边缘
        double sigma = 1.6
//这个是图像预处理时的模糊系数
        );
    
    int descriptorSize() const;//返回描述子长度,一般是128
    int descriptorType() cosnt;//返回描述子的元素类型,一般是CV_32F
...
};

使用SIFT类对象

先使用SIFT对象调用 detectAndCompute()接口,注意image是CV_8U类型,mask不使用设置成cv::noArray(),


virtual void detectAndCompute(
            cv::InputArray image, 
            cv::InputArray mask,
            vector<cv::keyPoint> & keypoints,
            cv::OutputArray descriptors,    //常用cv::Mat格式
            bool useProvidedKeypoints = false, 
                    //true就使用keypoints,false就自动检测
            );
 
int main()
{
	int numFeatrues = 100;          //给出关键点数量, 如果找到200个就取前100个
	Ptr<SIFT>detector = SIFT:create(numFeatrues);//使用了SIFT默认参数
	vector<KeyPoint> keypoints;
	detector->detect(src, keypoints, Mat());
	Mat keypoint_img;
	drawKeypoints(src, keypoints, keypoint_img, Scalar::all(-1), DrawMatchesFlags::DEFAULT);
	imshow("KeyPointsImage", keypoints_img);
}

openCV和SURF

SURF算法也是通过cv::xfeatures2d::SURF对象实现的,对于SURF类有:

hessianThreashold 设置Hessian行列式阈值,该阈值时为了将特定局部极值视为关键点所设.一般设置成1500, 设置成100表示全都要

extended表示使用128维特征集,一般描述子的元素个数是64, 扩展的是128

upright表示不需要计算特征方向,即默认为垂直,


class cv::xfeatures2d::SURF : public cv::Feature2D
{
public:
    static Ptr<SURF> create(
        double hessianThreshold = 100,
        int nOctaves = 4,
        int nOctaveLayers = 3,
        bool extended = false,
        bool upright = false,
        );
        
    int descriptorSize() const;
    int descriptorType() const;
...    
};
typedef SURF SurfFeatureDetector;

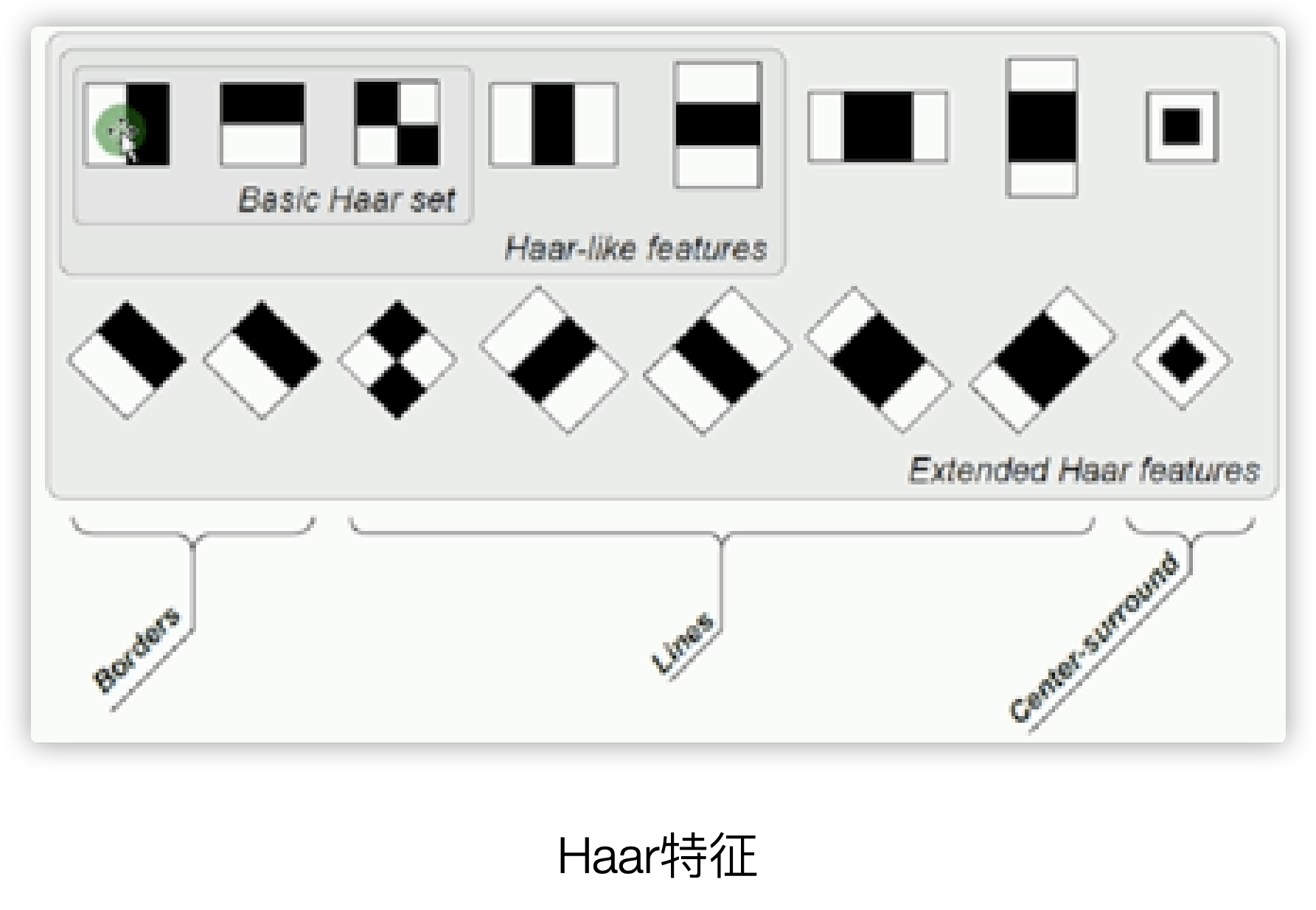
Haar特征(黑白色块)

Haar特征是按照黑白像素区域,每一个黑色或白色区域都是一个包含了多个像素的像素块,像素块之间的差值决定了哪些块之间存在哪种类型的边缘,比如下图的第一个是描述的垂直边缘,第二个则表示水平边缘.

一个矩形Haar特征定义了矩形中几个区域像素和的差值,可以是任意尺寸和任意位置,这个差值表明了图像的特定区域的某些特征

Haar特征往往应用在人脸识别的场景

角点

一般有: 边缘\ 角点\ 纹理

什么是角点?

角点就是极值点，即在某方面属性特别突出的点。

可以自己定义角点的属性（设置特定熵值进行角点检测）。

角点可以是两条线的交叉处，也可以是位于相邻的两个主要方向不同的事物上的点。

“角点”、“兴趣点”、“特征”在文献中的使用是相互间可替换的.

角点显然在一些方向上有明显的变化

人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。

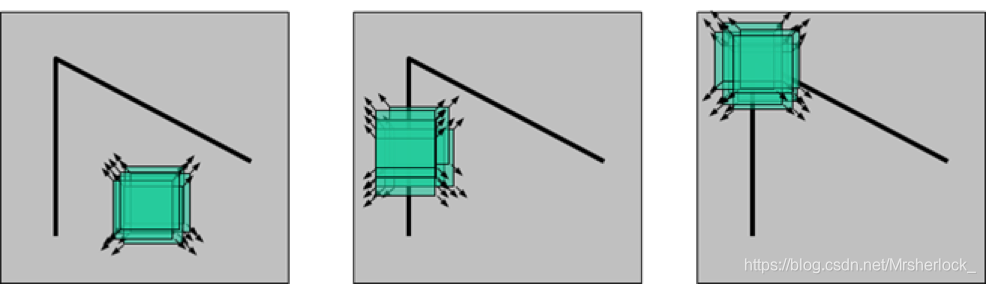
如果在各个方向上移动这个特征的小窗口，窗口内区域的灰度发生了较大的变化，那么就认为在窗口内遇到了角点。

如果这个特定的窗口在图像各个方向上移动时，窗口内图像的灰度没有发生变化，那么窗口内就不存在角点；

如果窗口在某一个方向移动时，窗口内图像的灰度发生了较大的变化，而在另一些方向上没有发生变化，那么，窗口内的图像可能就是一条直线的线段。

在现实世界中，角点对应于物体的拐角，道路的十字路口、丁字路口等。从图像分析的角度来定义角点可以有以下两种定义：

角点可以是两个边缘的角点；
角点是邻域内具有两个主方向的特征点；

前者往往需要对图像边缘进行编码，这在很大程度上依赖于图像的分割与边缘提取，具有相当大的难度和计算量，且一旦待检测目标局部发生变化，很可能导致操作的失败。

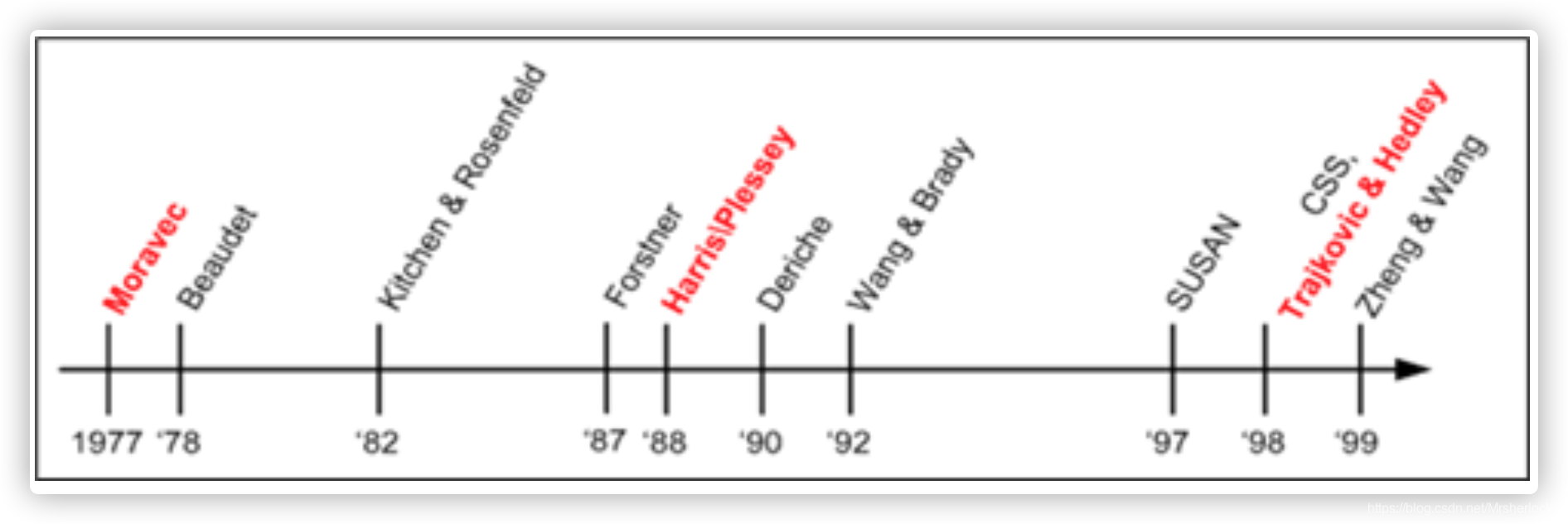
早期主要有Rosenfeld和Freeman等人的方法，后期有CSS等方法。

基于图像灰度的方法通过计算点的曲率及梯度来检测角点，避免了第一类方法存在的缺陷，此类方法主要有Moravec算子、Forstner算子、Harris算子、SUSAN算子等。

这篇文章主要介绍的Harris角点检测的算法原理，比较著名的角点检测方法还有jianbo Shi和Carlo Tomasi提出的Shi-Tomasi算法，这个算法开始主要是为了解决跟踪问题，用来衡量两幅图像的相似度，我们也可以把它看为Harris算法的改进。OpenCV中已经对它进行了实现，接口函数名为GoodFeaturesToTrack()。

另外还有一个著名的角点检测算子即SUSAN算子，SUSAN是Smallest Univalue Segment Assimilating Nucleus（最小核值相似区）的缩写。SUSAN使用一个圆形模板和一个圆的中心点，通过圆中心点像素与模板圆内其他像素值的比较，统计出与圆中心像素近似的像元数量，当这样的像元数量小于某一个阈值时，就被认为是要检测的角点。

可以把SUSAN算子看为Harris算法的一个简化。这个算法原理非常简单，算法效率也高，所以在OpenCV中，它的接口函数名称为：FAST()

Harris角点检测(重点)

原理

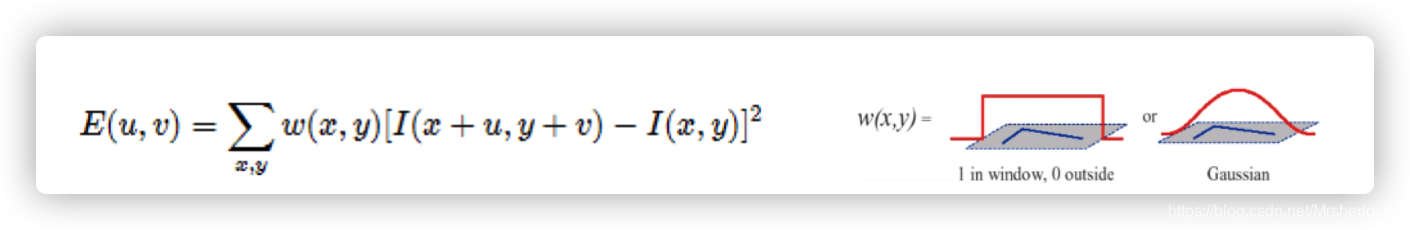
w(x,y)是权值公式,w是考虑到了Gaussian分布,也就是考虑到了邻域值的影响

角点, 就是任何方向都有变化的点, 就是考虑u和v取任意值的时候, 表达式都要很大

目标: 寻找角点, 即角点检测, 若是角点,则上述表达式则取值应在一个较大的范围,那么问题转换成:如何使得uv取任意值时该表达式值最大 ?

推理:

考虑泰勒公式,在a点的展开式:

对进行展开(忽略高阶项):

把结果带入公式E(u,v)部分项中:

把记为M,继续忽略w(x,y)项,对上述结果进行整理:

在uv取任意值时, 尽可能使的E很大, 依然忽略w(x,y), M矩阵是个特殊的矩阵, 对他相似对角化, 且带入E中,

结论: 根据上述结果, 发现: E 是一个标准的椭圆

让E无论u和v取值多少, 都很大,那就要λ1和λ2尽可能的大

问题转换成: 如何使得 λ1和λ2尽可能的大 ?

对表达式开根号,得到长半轴短半轴

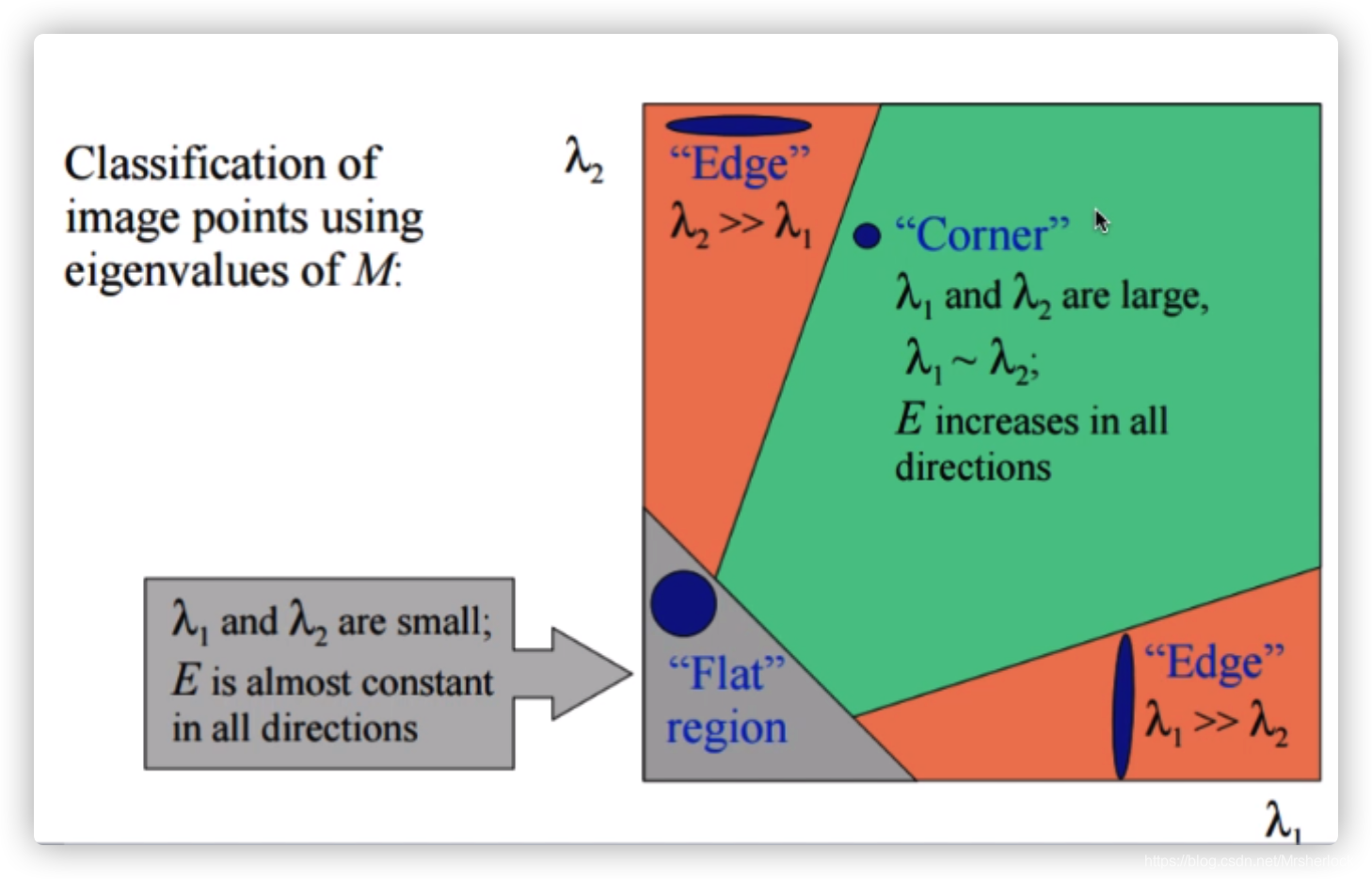
上述表明: λ1和λ2很大,且值近似时, E在各个方向增长最快, 很小且近似时,E趋于一个常量

引入其中,det是矩阵行列式, trace是矩阵的迹

综上,利用两个式子对像素进行评分:和

求R的方法有很多,可以先求出来M的特征值,根据特征值计算R,也可以直接求M的行列式和迹

R就是每个像素点的得分, 我们对每个像素都求一个R, 在局部图像中, R值最高的像素点就是角点

式中:Ix是对x求一阶导, 可以利用sobel解决, k是常数,取值在0.04-0.06 ,w()是考虑了高斯分布的权值公式

Harris角点的特性

1.参数k的影响:

直接影响的是: 角点的检测灵敏性与角点数量

推理:

由于将引入λ2=kλ1,因此将上述的参数k用a替代.注意区分

结论：增大α的值，将减小角点响应值R，降低角点检测的灵敏性，减少被检测角点的数量；减小α值，将增大角点响应值R，增加角点检测的灵敏性，增加被检测角点的数量。

2. Harris角点检测算子对亮度和对比度的变化不敏感

这是因为在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是，由于阈值的选择，可能会影响角点检测的数量。

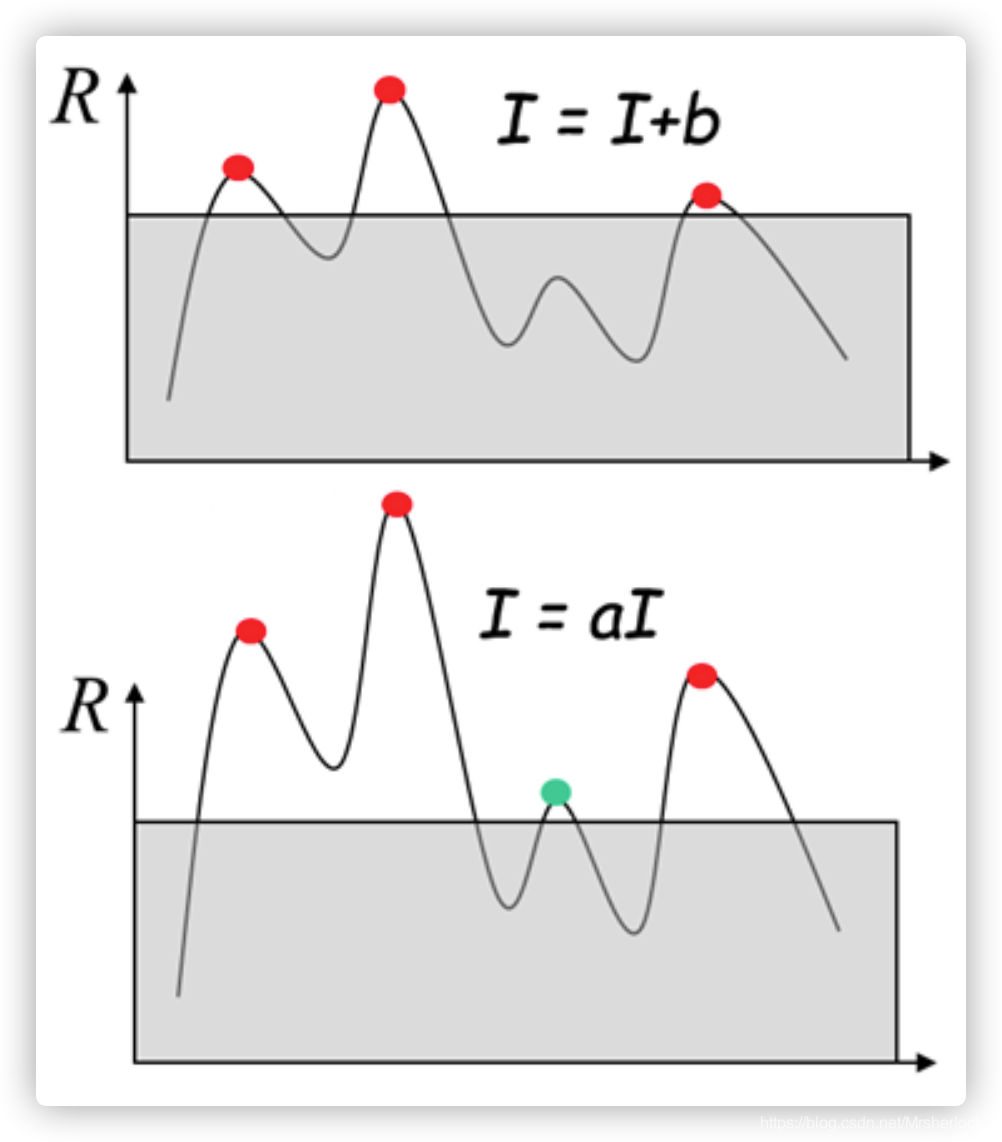
3. Harris角点检测算子具有旋转不变性

Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值RR也不发生变化，由此说明Harris角点检测算子具有旋转不变性。

4. Harris角点检测算子不具有尺度不变性

如下图所示，当右图被缩小时，在检测窗口尺寸不变的前提下，在窗口内所包含图像的内容是完全不同的。左侧的图像可能被检测为边缘或曲线，而右侧的图像则可能被检测为一个角点。

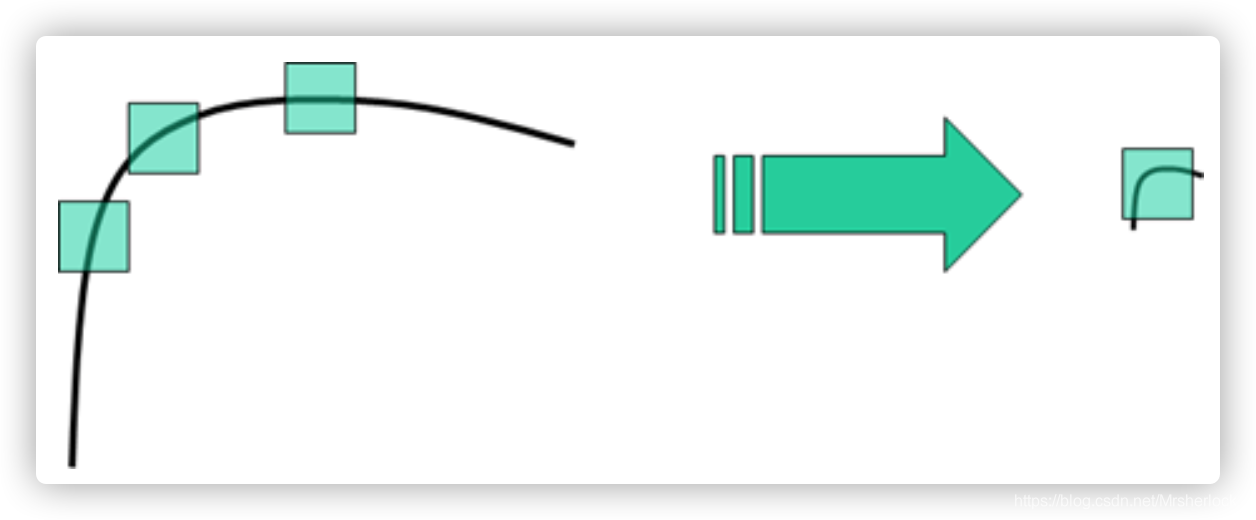
Harris角点检测的算法实现

另外, 需要对上述结果进行非最大值抑制,即: 在3×33×3或5×55×5的邻域内进行非最大值抑制，局部最大值点即为图像中的角点

非极大值抑制原理: 在一个窗口内，如果有多个角点则用值最大的那个角点，其他的角点都删除，窗口大小这里我们用3*3，程序中通过图像的膨胀运算来达到检测极大值的目的，因为默认参数的膨胀运算就是用窗口内的最大值替代当前的灰度值。

在openCV中的实现

我们需要对图像进行阈值化。针对灰度图像, 先cvtColor , 且输出像素类型要是浮点数,浮点值越高，表明越可能是特征角点


void cv::cornerHarris(InputArray src, OutputArray dst,
                        int blockSize,
                        int ksize,
                        double k,
                        int borderType = BORDER_DEFAULT)
 
/*
src – 输入的单通道8-bit或浮点图像。
dst – 存储着Harris角点响应的图像矩阵，大小与输入图像大小相同，是一个浮点型矩阵。
blockSize – 邻域大小。
ksize – 微分算子的大小(计算λ)
k – 响应公式中的，参数α
boderType – 边界处理的类型。borderType参考Opencv3学习文档里的边缘像素处理方法
*/
 
int main()
{
    Mat image = imread("../buliding.png");
    Mat gray;
    cvtColor(image, gray, CV_BGR2GRAY);
 
    Mat cornerStrength;
    cornerHarris(gray, cornerStrength, 3, 3, 0.01);
    threshold(cornerStrength, cornerStrength, 0.001, 255, THRESH_BINARY);
    return 0;
}

加入非极大值抑制


int main()
{
    Mat image = imread("buliding.png");
    Mat gray;
    cvtColor(image, gray, CV_BGR2GRAY);
 
    Mat cornerStrength;
    cornerHarris(gray, cornerStrength, 3, 3, 0.01);
 
    double maxStrength;
    double minStrength;
    // 找到图像中的最大、最小值
    minMaxLoc(cornerStrength, &minStrength, &maxStrength);
 
    Mat dilated;
    Mat locaMax;
    // 膨胀图像，最找出图像中全部的局部最大值点
    dilate(cornerStrength, dilated, Mat());
    // compare是一个逻辑比较函数，返回两幅图像中对应点相同的二值图像
    compare(cornerStrength, dilated, locaMax, CMP_EQ);
 
    Mat cornerMap;
    double qualityLevel = 0.01;
    double th = qualityLevel*maxStrength; // 阈值计算
    threshold(cornerStrength, cornerMap, th, 255, THRESH_BINARY);
    cornerMap.convertTo(cornerMap, CV_8U);
    // 逐点的位运算
    bitwise_and(cornerMap, locaMax, cornerMap);
 
    drawCornerOnImage(image, cornerMap);
    namedWindow("result");
    imshow("result", image);
    waitKey();
 
    return 0;
}
void drawCornerOnImage(Mat& image, const Mat&binary)
{
    Mat_<uchar>::const_iterator it = binary.begin<uchar>();
    Mat_<uchar>::const_iterator itd = binary.end<uchar>();
    for (int i = 0; it != itd; it++, i++)
    {
        if (*it)
            circle(image, Point(i%image.cols, i / image.cols), 3, Scalar(0, 255, 0), 1);
    }
}

结果对比

多尺度Harris角点检测

理论:

虽然Harris角点检测算子具有部分图像灰度变化的不变性和旋转不变性，但它不具有尺度不变性。但是尺度不变性对图像特征来说至关重要。

人们在使用肉眼识别物体时，不管物体远近，尺寸的变化都能认识物体，这是因为人的眼睛在辨识物体时具有较强的尺度不变性。

在图像特征提取：尺度空间理论这篇文章里就已经讲到了高斯尺度空间的概念。Shi-Tomasi角点检测Shi-Tomasi角点检测Shi-Tomasi角点检测Shi-Tomasi角点检测下面将Harris角点检测算子与高斯尺度空间表示相结合，使Harris角点检测算子具有尺度的不变性。

实现:

特征点的方法，可以处理明显的仿射变换，包括大尺度变化和明显的视角变化。Harris-Affine主要是依据了以下三个思路：

特征点周围的二阶矩的计算对区域进行的归一化，具有仿射不变性；
通过在尺度空间上归一化微分的局部极大值求解来精化对应尺度；
自适应仿射Harris检测器能够精确定位牲点；


#include "imgFeat.h"
 
void feat::detectHarrisLaplace(const Mat& imgSrc, Mat& imgDst)
{
	Mat gray;
	if (imgSrc.channels() == 3)
	{
		cvtColor(imgSrc, gray, CV_BGR2GRAY);
	}
	else
	{
		gray = imgSrc.clone();
	}
	gray.convertTo(gray, CV_64F);
 
	/* 尺度设置*/
	double dSigmaStart = 1.5;
	double dSigmaStep = 1.2;
	int iSigmaNb = 13;
 
	vector<double> dvecSigma(iSigmaNb);
	for (int i = 0; i < iSigmaNb; i++)
	{
		dvecSigma[i] = dSigmaStart + i*dSigmaStep;
	}
	vector<Mat> harrisArray(iSigmaNb);
	
	for (int i = 0; i < iSigmaNb; i++)
	{
		double iSigmaI = dvecSigma[i];
		double iSigmaD = 0.7 * iSigmaI;
 
		int iKernelSize = 6*round(iSigmaD) + 1;
		/*微分算子*/
		Mat dx(1, iKernelSize, CV_64F);
		for (int k =0; k < iKernelSize; k++)
		{
			int pCent = (iKernelSize - 1) / 2;
			int x = k - pCent;
			dx.at<double>(0,i) = x * exp(-x*x/(2*iSigmaD*iSigmaD))/(iSigmaD*iSigmaD*iSigmaD*sqrt(2*CV_PI));
		}
	
		Mat dy = dx.t();
		Mat Ix,Iy;
		/*图像微分*/
		filter2D(gray, Ix, CV_64F, dx);
		filter2D(gray, Iy, CV_64F, dy);
 
		Mat Ix2,Iy2,Ixy;
		Ix2 = Ix.mul(Ix);
		Iy2 = Iy.mul(Iy);
		Ixy = Ix.mul(Iy);
 
		int gSize = 6*round(iSigmaI) + 1;
		Mat gaussKernel = getGaussianKernel(gSize, iSigmaI);
		filter2D(Ix2, Ix2, CV_64F, gaussKernel);
		filter2D(Iy2, Iy2, CV_64F, gaussKernel);
		filter2D(Ixy, Ixy, CV_64F, gaussKernel);
 
		/*自相关矩阵*/
		double alpha = 0.06;
		Mat detM = Ix2.mul(Iy2) - Ixy.mul(Ixy);
		Mat trace = Ix2 + Iy2;
		Mat cornerStrength = detM - alpha * trace.mul(trace);
 
		
 
		double maxStrength;
		minMaxLoc(cornerStrength, NULL, &maxStrength, NULL, NULL);
		Mat dilated;
		Mat localMax;
		dilate(cornerStrength, dilated, Mat());
		compare(cornerStrength, dilated, localMax, CMP_EQ);
	
 
		Mat cornerMap;
		double qualityLevel = 0.2;
		double thresh = qualityLevel * maxStrength;
		cornerMap = cornerStrength > thresh;
		bitwise_and(cornerMap, localMax, cornerMap);
		harrisArray[i] = cornerMap.clone();	
	}
 
	/*计算尺度归一化Laplace算子*/
	vector<Mat> laplaceSnlo(iSigmaNb);
	for (int i = 0; i < iSigmaNb; i++)
	{
		double iSigmaL = dvecSigma[i];
		Size kSize = Size(6 * floor(iSigmaL) +1, 6 * floor(iSigmaL) +1);
		Mat hogKernel = getHOGKernel(kSize,iSigmaL);
		filter2D(gray, laplaceSnlo[i], CV_64F, hogKernel);
		laplaceSnlo[i] *= (iSigmaL * iSigmaL);
	}
	
	/*检测每个特征点在某一尺度LOG相应是否达到最大*/
	Mat corners(gray.size(), CV_8U, Scalar(0));
	for (int i = 0; i < iSigmaNb; i++)
	{
		for (int r = 0; r < gray.rows; r++)
		{
			for (int c = 0; c < gray.cols; c++)
			{
				if (i ==0)
				{
					if (harrisArray[i].at<uchar>(r,c) > 0 && laplaceSnlo[i].at<double>(r,c) > laplaceSnlo[i + 1].at<double>(r,c))
					{
						corners.at<uchar>(r,c) = 255;
					}
				}
				else if(i == iSigmaNb -1)
				{
					if (harrisArray[i].at<uchar>(r,c) > 0 && laplaceSnlo[i].at<double>(r,c) > laplaceSnlo[i - 1].at<double>(r,c))
					{
						corners.at<uchar>(r,c) = 255;
					}
				}
				else
				{
					if (harrisArray[i].at<uchar>(r,c) > 0 &&
					laplaceSnlo[i].at<double>(r,c) > laplaceSnlo[i + 1].at<double>(r,c) &&
					laplaceSnlo[i].at<double>(r,c) > laplaceSnlo[i - 1].at<double>(r,c))
					{
						corners.at<uchar>(r,c) = 255;
					}
				}
			}
		}
	}
	imgDst = corners.clone();
	
}

Shi-Tomasi角点检测

区别于Harris角点检测, Shi-Tomasi角点检测,只是把R的取值方式改变了, 就是打分的方式换了

注意,这里的k取值为0.04-0.06


void cv::goodFeaturesToTrack(InputArray image,
                            OutputArray corners,
                            int maxCorners,
                            double qualityLevel,
                            double minDistance,
                            int blockSize = 3,
                            bool useHarrisDetector = false,
                            double k = 0.04);
/*第一个参数image：8位或32位单通道灰度图像;
  第二个参数corners: 位置点向量,保存的是检测到角点的坐标, 坐标是Point类型, 结果放到vector中,可以存储多个Point类型的坐标
  第三个参数maxCorners: 定义可以检测到的角点的数量的最大, 如果检测出来200个, 我想要100个,那就从200中选择前100个;
  第四个参数qualityLevel: 检测到的角点的质量等级,角点特征值小于qualityLevel*最大特征值的点将被舍弃;
  第五个参数minDistance: 两个角点间最小间距,以像素为单位;
  第六个参数mask: 指定检测区域,若检测整幅图像,mask置为空Mat();
  第七个参数blockSize: 计算协方差矩阵时窗口大小;
  第八个参数useHarrisDector: 是否使用Harris角点检测,为false,则使用Shi-Tomasi算子;
  第九个参数K: 留给Harris角点检测算子用的中间参数,一般取经验值0.04~0.06.第8个参数为false时,改参数不起作用;
*/
 
 
 
	vector<Point2f>corners;
	double qualityLevel = 0.01;
	double minDistance = 10;
	int blockSize = 3;
	double useHarris = false;
	double k = 0.04;
	Mat resulting = src.clone();
	goodFeaturesToTrack(src_gray, corners, max_corners, 
qualityLevel, minDistance, Mat(), blockSize, useHarris, k);

自定义角点检测

在OpenCV中已经为我们提供了相关函数——cornerHarris() 函数和 goodFeaturesToTrack()函数，分别来实现Harris角点检测和Shi-Tomasi角点检测;

除此之外，其实我们也可以根据算法的原理和需求来制作角点检测的函数。

例如:使用cornerEigenValsAndVecs()函数和minMaxLoc()函数结合来模拟Harris角点检测，或者使用cornerMinEigenVal()函数和minMaxLoc()函数结合来模拟Shi-Tomasi角点检测，最后特征点选取的判断条件要根据实际情况进行选择。

cornerEigenValsAndVecs()函数

cornerEigenValsAndVecs()函数用来求解输入图像矩阵的特征向量与特征值


 
/*
src：输入图像矩阵，即单通道8位或者浮点类型的图像。
dst：输出矩阵，即用来存储结果的图像，大小与输入图像一致并且为CV_32FC(6)类型。
计算自相关矩阵M的特征值和特征向量，并将它们以(λ1, λ2, x1, y1, x2,y2)的形式存储在目标图像dst中。
其中λ1, λ2是M未经过排序的特征值；x1, y1是对应于λ1的特征向量；x2, y2是对应于λ2的特征向量。因此是6通道的矩阵。
blockSize：邻域大小。
ksize：Sobel算子当中的核大小，只能取1、3、5、7。
borderType：像素扩展的方法。
*/

cornerMinEigenVal()函数

功能与cornerEigenValsAndVecs()函数相似，但是它只计算导数协方差矩阵（即自相关矩阵）的最小特征值，


 
 
/*        
        src：输入图像矩阵，即单通道8位或者浮点类型的图像。
        dst：输出矩阵，即用来存储结果的图像，大小与输入图像一致并且为CV_32FC(1)类型, 因为是只计算一个结果, 所以是单通道
        blockSize：邻域大小。
        ksize：Sobel算子当中的核大小，只能取1、3、5、7。
        borderType：像素扩展的方法。
*/

minMaxLoc()函数

minMaxLoc()函数寻找输入矩阵（在c++中就是Mat对象）中的最小值和最大值，同时可以其相应值的位置（Point对象）。


 
/*
        src：输入矩阵。
        minVal：找到的最小值，double *类型。
        maxVal：找到的最大值，double *类型。
        minLoc、maxLoc：都是Point *类型的变量，用来存所找到的最大值和最小值的坐标，即Point坐标。
        mask：如果是对整个图像区域搜索，指定为Mat()即可。
如果参数maxVal、minLoc、maxLoc不需要，只需指定为NULL或者0即可。
*/

自定义角点检测实现


#include <opencv2/opencv.hpp>
#include <iostream>
#include <math.h>
 
using namespace cv;
using namespace std;
 
// 定义全局变量
const string harris_winName = "自定义角点检测";
Mat src_img, gray_img;                       // src_img表示原图, gray_img表示灰度图
Mat harris_dst_img, harris_response_img;     // harris_dst_img存储自相关矩阵M的特征值和特征向量，harris_response_img存储响应函数的结果
//通过响应公式R=λ1*λ2 - k*(λ1+λ2)*(λ1+λ2)来计算每个像素对应的响应值
double min_respense_value;			  // 响应函数的结果矩阵中的最小值
double max_respense_value;			  // 响应函数的结果矩阵中的最大值
 
int qualityValue = 30;
int max_qualityValue = 100;              // 通过qualityValue/max_qualityValue的结果作为qualitylevel来计算阈值
RNG  random_number_generator;             // 定义一个随机数发生器
void self_defining_Harris_Demo(int, void*);      //TrackBar回调函数声明
 
// 主函数
int main()
{
	src_img = imread("test11.png");
	if (src_img.empty())
	{
		printf("could not load the image...\n");
		return -1;
	}
	namedWindow("原图", CV_WINDOW_AUTOSIZE);
	imshow("原图", src_img);
	cvtColor(src_img, gray_img, COLOR_BGR2GRAY);      //将彩色图转化为灰度图
 
	// 计算特征值
	int blockSize = 3;
	int ksize = 3;
	double k = 0.04;
	harris_dst_img = Mat::zeros(src_img.size(), CV_32FC(6));
	// 目标图像harris_dst_img存储自相关矩阵M的特征值和特征向量，
	// 并将它们以(λ1, λ2, x1, y1, x2, y2)的形式存储。其中λ1, λ2是M未经过排序的特征值；
	// x1, y1是对应于λ1的特征向量；x2, y2是对应于λ2的特征向量。
	// 因此目标矩阵为6通道，即 CV_32FC(6)的矩阵。
 
	harris_response_img = Mat::zeros(src_img.size(), CV_32FC1);
	// harris_response_img用来存储通过每个像素值所对应的自相关矩阵所计算得到的响应值
 
	cornerEigenValsAndVecs(gray_img, harris_dst_img, blockSize, ksize, 4);
	// 该函数用来计算每个像素值对应的自相关矩阵的特征值和特征向量
 
	// 计算响应函数值
	for (int row = 0; row < harris_dst_img.rows; ++row)
	{
		for (int col = 0; col < harris_dst_img.cols; ++col)
		{
			double eigenvalue1 = harris_dst_img.at<Vec6f>(row, col)[0];     // 获取特征值1
			double eigenvalue2 = harris_dst_img.at<Vec6f>(row, col)[1];		// 获取特征值2
			harris_response_img.at<float>(row, col) = eigenvalue1 * eigenvalue2 - k * pow((eigenvalue1 + eigenvalue2), 2);
			// 通过响应公式R=λ1*λ2 - k*(λ1+λ2)*(λ1+λ2)来计算每个像素对应的响应值
		}
	}
	minMaxLoc(harris_response_img, &min_respense_value, &max_respense_value, 0, 0, Mat());   // 寻找响应矩阵中的最小值和最大值
	namedWindow(harris_winName, CV_WINDOW_AUTOSIZE);
	createTrackbar("Quality Value:", harris_winName, &qualityValue, max_qualityValue, self_defining_Harris_Demo);    //创建TrackBar
	self_defining_Harris_Demo(0, 0);
 
	waitKey(0);
	return 0;
}
 
 
//  回调函数实现
void self_defining_Harris_Demo(int, void*)
{
	if (qualityValue < 10)
	{
		qualityValue = 10;       // 控制qualitylevel的下限值
	}
	Mat result_img = src_img.clone();    // 输出图像
	float threshold_value = min_respense_value + (((double)qualityValue) / max_qualityValue)*(max_respense_value - min_respense_value);
	for (int row = 0; row < result_img.rows; row++)
	{
		for (int col = 0; col < result_img.cols; col++)
		{
			float resp_value = harris_response_img.at<float>(row, col);
			if (resp_value > threshold_value)
			{
				circle(result_img, Point(col, row), 2, Scalar(random_number_generator.uniform(0, 255),
					random_number_generator.uniform(0, 255), random_number_generator.uniform(0, 255)), 2, 8, 0);
			}
		}
	}
	imshow(harris_winName, result_img);
}

亚像素级别角点检测

说白了, 就是像素不是整数的像素

亚像素定位, 插值方法, 基于图像矩计算, 曲线拟合方法(高斯曲面,多项式,椭圆)

之前用的Harris和Shi-Tomasi进行角点检测时得到的都是自己想要的角点，这些角点的坐标都是粗略的，要想得到最完美的角点检测就是利用亚像素级角点检测

若我们进行的不是图像处理的识别特征点而是进行几何测量，通常需要更高的精度前两种角点检测只能提供简单像素的坐标值，也就是说有时候会需要实数坐标值而不是整数坐标值。

1.检测步骤.

亚像素级角点检测的位置在摄像机标定，跟踪并重建摄像机的轨迹，或者重建被跟踪目标的三维结构时，是一个基本的测量值,一般都是根据角点的位置–退出位置精确的亚像素级精度，一个向量和其正交的向量的点积为0

第一步就是先确定角点的位置用Harris或者Shi-Tomasi来进行求取角点，

第二步,由这些角点再来计算亚像素级角点的具体位置Opencv为我们提供了cornerSubPix()函数用于寻找亚像素级角点的位置的。

2.cornerSubPix()函数寻找角点时（不是整数类型的位置，而是更加精确的浮点类型位置）


C++:void cornerSubPix(InputArray img,
InputOutputArray corner,
Size winSize,
Size zeroZone,
TermCriteria criteria
);

首先说明最主要的是参数二：表示输入输出的二维点vector corners类型的，作为输入时表示由Harris角点检测之后返回的角点，首先遍历角点，把角点push_back到二维点容器中，然后在放到亚像素级角点检测函数中作为输入，输出的时候就是亚像素级的2维坐标点，即Point类型进行遍历显示既可以，同时由Shi-Tomasi角点检测出来的角点直接放入亚像素级角点检测中去作为输入，输出就是亚像素级别的角点

参数详细说明:

1.输入的图像一般是灰度图像

2.Input和Output类型的角点，输入是角点的初始坐标点，输出是精准的输出坐标

3.Size类型的winSize，搜索窗口的一半尺寸，搜索窗口就是2倍的关系

4.Size类型的zeroZone，表示死区的一半尺寸值为（-1，-1）表示无死区。

5.求角点的迭代过程的终止条件

总之在进行亚像素级的角点检测时：

1.Harris角点检测配合cornerSubPix()函数（注意参数的准备）可以求出精确的角点

2.Shi-Tomasi角点检测配合cornerSubPix()函数（注意参数的准备）可以求出精确的角点

TermCriteria()模板类

类功能：模板类，作为迭代算法的终止条件。
构造函数:


TermCriteria(int type,
 
int maxCount,
 
double epsilon
 
);

参数说明：

type 迭代终止条件类型

type=TermCriteria::MAX_ITER/TermCriteria::COUNT 迭代到最大迭代次数终止

type= TermCriteria::EPS 迭代到阈值终止

type= TermCriteria::MAX_ITER+ TermCriteria::EPS 上述两者都作为迭代终止条件

maxCount 迭代的最大次数

epsilon 阈值(中心位移值)

调用参考：

cv::TermCriteria criteria(cv::TermCriteria::MAX_ITER,10,0.01);

最终输出了亚像素值的坐标点

可以看出来cornerSubPix()的参数corners是Point类型

LBP特征检测

没有看LBP之前觉得它很神秘，看完了之后也就那么回事，不过提出LBP的人确实很伟大！！

　　LBP（Local Binary Pattern，局部二值模式）是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出，用于纹理特征提取。而且，提取的特征是图像的局部的纹理特征；

LBP是Local Binary Pattern局部二值模式的缩写,LBP特征描述的是图像的局部特征,

LBP特征的特点是旋转不变性和灰度不变性

常用在人脸识别和目标检测上

LBP的旋转不变性和灰度不变性,往往可以对光照,旋转等具有较强的鲁棒性

1、LBP特征的描述

原始的LBP算子定义为在3*3的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数（通常转换为十进制数即LBP码，共256种），即得到该窗口中心像素点的LBP值，并用这个值来反映该区域的纹理信息。

基本的 LBP 算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要

综上所述, 在一张图片或一个感兴趣区域中,其LBP特征有如下描述步骤:

在灰度图片中,在3x3的像素邻域内,以中心像素作为阈值T,将中心点的8邻域像素的8个数值,分别和T进行比较,若大于T则置1,小于则0
把第一步的8个比较结果,依次排成一行,形成一个8位二进制序列,并转换成十进制数值
十进制结果即该中心像素的LBP特征值

显然,一个像素点,可以生成2^8=256种LBP特征值

原始LBP由于采用固定邻域像素点作为比较对象,所以面对尺寸变换时往往失去鲁棒性,更不要谈旋转不变性了

如下图所示：

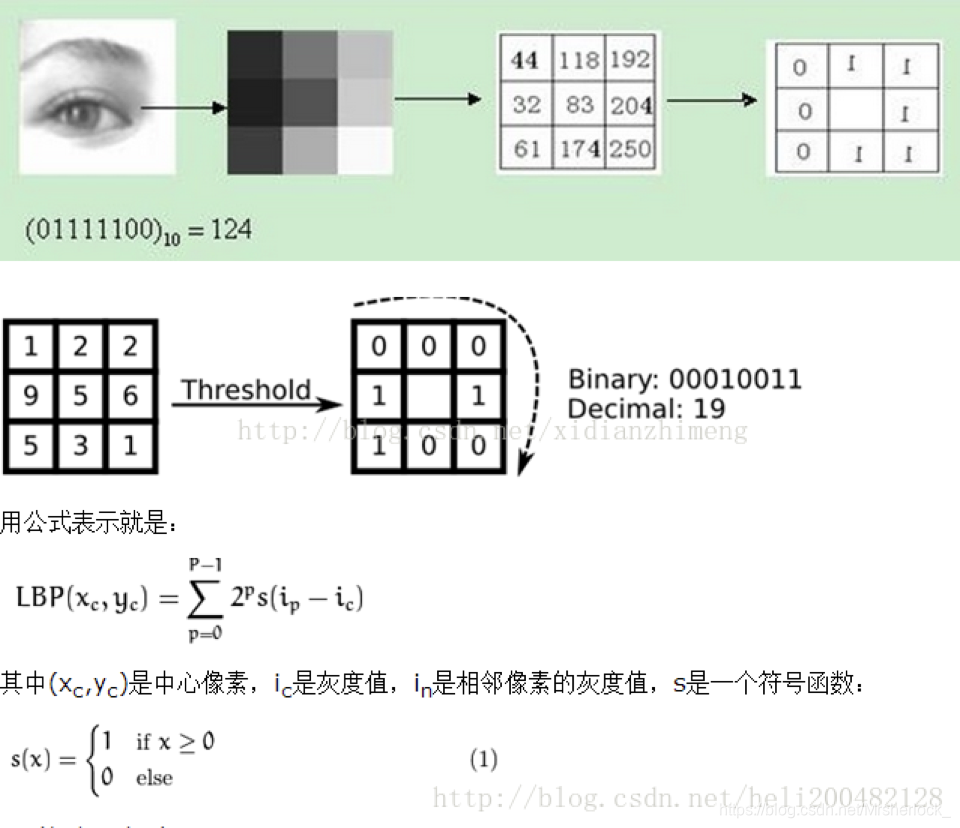
LBP的改进版本：

　　原始的LBP提出后，研究人员不断对其提出了各种改进和优化。

圆形LBP算子：

　　基本的 LBP 算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要。

为了适应不同尺度的纹理特征，并达到灰度和旋转不变性的要求，Ojala 等对 LBP 算子进行了改进，将 3×3 邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子；

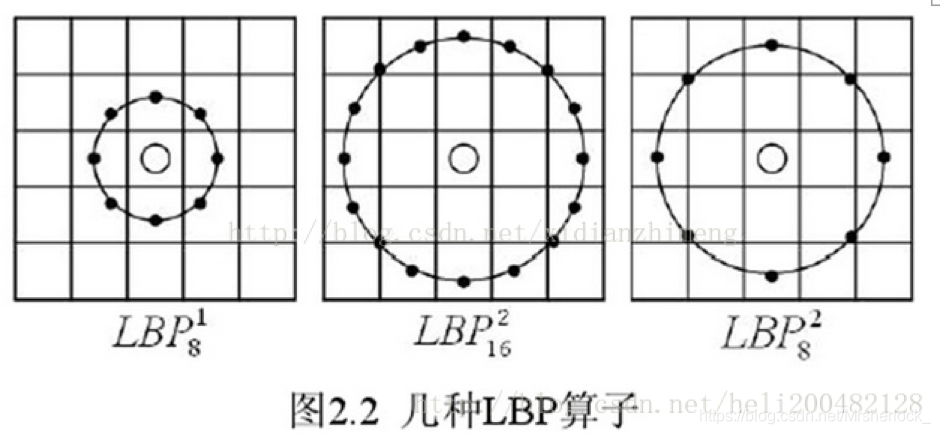
　　从 LBP 的定义可以看出，LBP 算子是灰度不变的，但却不是旋转不变的。图像的旋转就会得到不同的 LBP值, 这里应该是说的基本的LBP, 圆形LBP是具有旋转不变性的.

Maenpaa等人又将 LBP 算子进行了扩展，提出了具有旋转不变性的 LBP 算子，即不断旋转圆形邻域得到一系列初始定义的 LBP 值，取其最小值作为该邻域的 LBP 值。　　

图 2.5 给出了求取旋转不变的 LBP 的过程示意图，图中算子下方的数字表示该算子对应的 LBP 值，图中所示的 8 种 LBP模式，经过旋转不变的处理，最终得到的具有旋转不变性的 LBP 值为 15。也就是说，图中的 8 种 LBP 模式对应的旋转不变的 LBP 模式都是00001111。

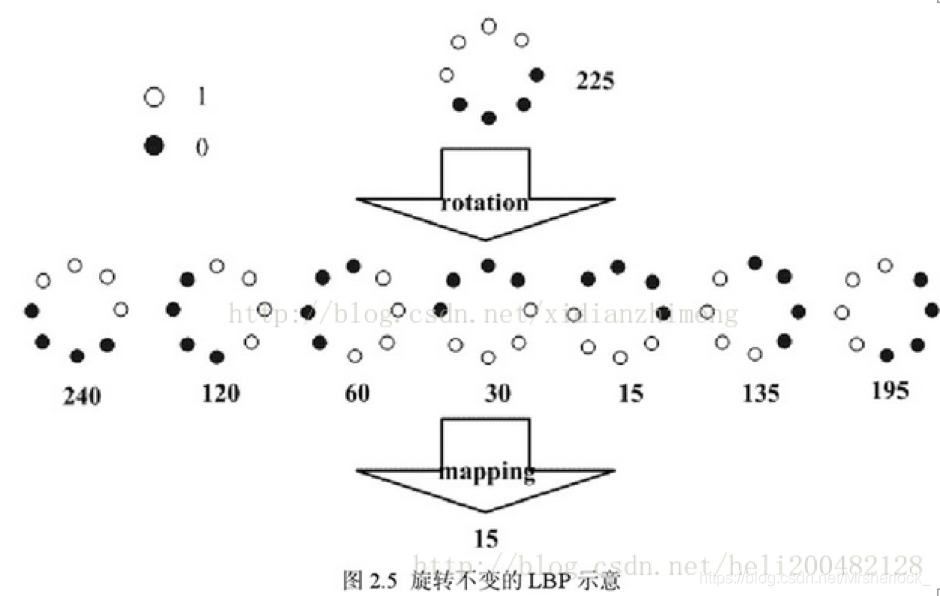
综上所述,

在CircularLBP特征中,保留了LBP的基本思想,具有如下描述步骤:

在灰度图片中,以某个像素点作为中心点,以R为半径画圆,圆的周长覆盖到的像素点,就是待和中心点比较的像素点
若圆周长覆盖的像素点不在图像内,就要采用差值算法,一般是双线性差值
对于CircularLBP所述的圆圈覆盖的邻域像素,按照一定步长进行角度旋转,得到一系列的序列(下图白点为1黑点为0),转换成LBP值,则每个像素点会有多个LBP值
取上述LBP值中最小的值作为该中心像素点的CircularLBP特征值

LBP等价模式

　　一个LBP算子可以产生不同的二进制模式，对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生2^p种模式。很显然，随着邻域集内采样点数的增加，二进制模式的种类是急剧增加的。例如：5×5邻域内20个采样点，有2^20＝1,048,576种二进制模式。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。同时，过多的模式种类对于纹理的表达是不利的。例如，将LBP算子用于纹理分类或人脸识别时，常采用LBP模式的统计直方图来表达图像的信息，而较多的模式种类将使得数据量过大，且直方图过于稀疏。

因此，需要对原始的LBP模式进行降维，使得数据量减少的情况下能最好的代表图像的信息。　　

为了解决二进制模式过多的问题，提高统计性，Ojala提出了采用一种“等价模式”（Uniform Pattern）来对LBP算子的模式种类进行降维。

Ojala等认为，在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此，Ojala将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。如00000000（0次跳变），00000111（只含一次从0到1的跳变），10001111（先由1跳到0，再由0跳到1，共两次跳变）都是等价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111（共四次跳变）（这是我的个人理解，不知道对不对）。　　

通过这样的改进，二进制模式的种类大大减少，而不会丢失任何信息。模式数量由原来的2P2P种减少为 P ( P-1)+2种，其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说，二进制模式由原始的256种减少为58种，这使得特征向量的维数更少，并且可以减少高频噪声带来的影响。

LBP特征用于检测的原理

　　显而易见的是，上述提取的LBP算子在每个像素点都可以得到一个LBP“编码”，那么，对一幅图像（记录的是每个像素点的灰度值）提取其原始的LBP算子之后，得到的原始LBP特征依然是“一幅图片”（记录的是每个像素点的LBP值）。

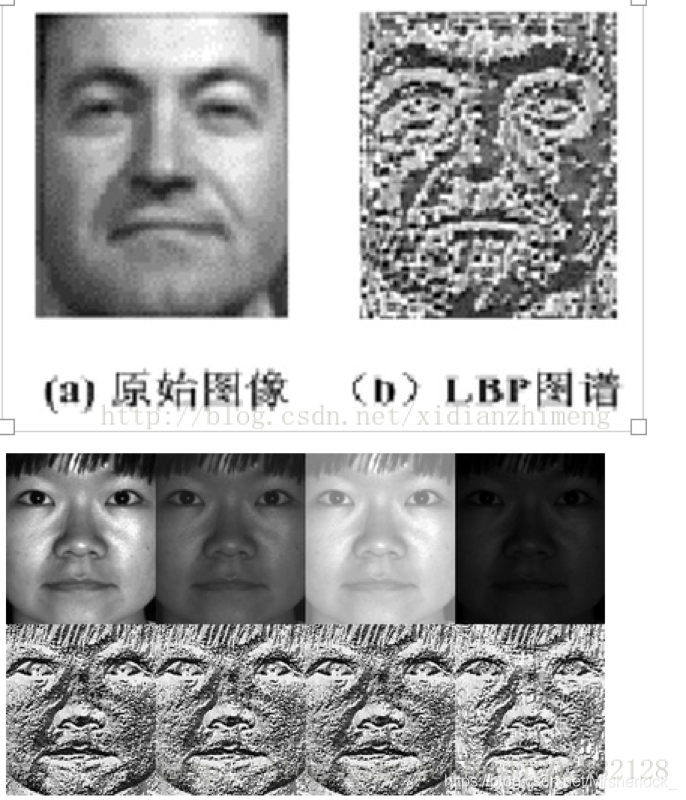
从上图可以看出LBP对光照具有很强的鲁棒性　　

LBP的应用中，如纹理分类、人脸分析等，一般都不将LBP图谱作为特征向量用于分类识别，而是采用LBP特征谱的统计直方图作为特征向量用于分类识别。　　

因为，从上面的分析我们可以看出，这个“特征”跟位置信息是紧密相关的。

直接对两幅图片提取这种“特征”，并进行判别分析的话，会因为“位置没有对准”而产生很大的误差。后来，研究人员发现，可以将一幅图片划分为若干的子区域，对每个子区域内的每个像素点都提取LBP特征，然后，在每个子区域内建立LBP特征的统计直方图。如此一来，每个子区域，就可以用一个统计直方图来进行描述；整个图片就由若干个统计直方图组成；　　

例如：一幅100*100像素大小的图片，划分为10*10=100个子区域（可以通过多种方式来划分区域），每个子区域的大小为10*10像素；在每个子区域内的每个像素点，提取其LBP特征，然后，建立统计直方图；这样，这幅图片就有10*10个子区域，也就有了10*10个统计直方图，利用这10*10个统计直方图，就可以描述这幅图片了。之后，我们利用各种相似性度量函数，就可以判断两幅图像之间的相似性了；

对LBP特征向量进行提取的步骤

　　（1）首先将检测窗口划分为16×16的小区域（cell）；　　

（2）对于每个cell中的一个像素，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数，即得到该窗口中心像素点的LBP值；　　

（3）然后计算每个cell的直方图，即每个数字（假定是十进制数LBP值）出现的频率；然后对该直方图进行归一化处理。　　

（4）最后将得到的每个cell的统计直方图进行连接成为一个特征向量，也就是整幅图的LBP纹理特征向量；　

(5)然后便可利用SVM或者其他机器学习算法进行分类了。

SIFT特征检测

1.SIFT概述

SIFT的全称是Scale Invariant Feature Transform，尺度不变特征变换，由加拿大教授David G.Lowe提出的。

SIFT特征对旋转、尺度缩放、亮度变化等保持不变性，是一种非常稳定的局部特征。

尺度不变特征转换(Scale-invariant feature transform或SIFT)是一种电脑视觉的算法用来侦测与描述影像中的局部性特征，它在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量，此算法由 David Lowe在1999年所发表，2004年完善总结。

其应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对。

此算法有其专利，专利拥有者为英属哥伦比亚大学。

局部影像特征的描述与侦测可以帮助辨识物体，SIFT 特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。使用 SIFT特征描述对于部分物体遮蔽的侦测率也相当高，甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。在现今的电脑硬件速度下和小型的特征数据库条件下，辨识速度可接近即时运算。

SIFT特征的信息量大，适合在海量数据库中快速准确匹配。

1.1 SIFT算法具的特点

图像的局部特征，对旋转、尺度缩放、亮度变化保持不变，对视角变化、仿射变换、噪声也保持一定程度的稳定性。
独特性好，信息量丰富，适用于海量特征库进行快速、准确的匹配。
多量性，即使是很少几个物体也可以产生大量的SIFT特征;
高速性，经优化的SIFT匹配算法甚至可以达到实时性;
扩招性，可以很方便的与其他的特征向量进行联合。

1.2 SIFT特征检测的步骤

有4个主要步骤

尺度空间的极值检测 搜索所有尺度空间上的图像，通过高斯微分函数来识别潜在的对尺度和选择不变的兴趣点。
特征点定位 在每个候选的位置上，通过一个拟合精细模型来确定位置尺度，关键点的选取依据他们的稳定程度。
特征方向赋值 基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向，后续的所有操作都是对于关键点的方向、尺度和位置进行变换，从而提供这些特征的不变性。
特征点描述 在每个特征点周围的邻域内，在选定的尺度上测量图像的局部梯度，这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变换。

加深理解:

SIFT是在不同的尺度空间上查找关键点(特征点)，并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等。

Lowe将SIFT算法分解为如下四步：

1. 尺度空间极值检测：搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。

2. 关键点定位：在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。

3. 方向确定：基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换，从而提供对于这些变换的不变性。

4. 关键点描述：在每个关键点周围的邻域内，在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变化。

本文沿着Lowe的步骤，参考Rob Hess及Andrea Vedaldi源码，详解SIFT算法的实现过程。

1.3 SIFT算法可以解决的问题：

目标的自身状态、场景所处的环境和成像器材的成像特性等因素影响图像配准/目标识别跟踪的性能。而SIFT算法在一定程度上可解决：

1. 目标的旋转、缩放、平移（RST）

2. 图像仿射/投影变换（视点viewpoint）

3. 光照影响（illumination）

4. 目标遮挡（occlusion）

5. 杂物场景（clutter）

6. 噪声

2. 尺度空间

在一定的范围内，无论物体是大还是小，人眼都可以分辨出来。然而计算机要有相同的能力却不是那么的容易，在未知的场景中，计算机视觉并不能提供物体的尺度大小，其中的一种方法是把物体不同尺度下的图像都提供给机器，让机器能够对物体在不同的尺度下有一个统一的认知。在建立统一认知的过程中，要考虑的就是在图像在不同的尺度下都存在的特征点。

尺度空间使用高斯金字塔表示。Tony Lindeberg指出尺度规范化的LoG(Laplacion of Gaussian)算子具有真正的尺度不变性，Lowe使用高斯差分金字塔近似LoG算子，在尺度空间检测稳定的关键点。

尺度空间(scale space)思想最早是由Iijima于1962年提出的，后经witkin和Koenderink等人的推广逐渐得到关注，在计算机视觉邻域使用广泛。

尺度空间理论的基本思想是：在图像信息处理模型中引入一个被视为尺度的参数，通过连续变化尺度参数获得多尺度下的尺度空间表示序列，对这些序列进行尺度空间主轮廓的提取，并以该主轮廓作为一种特征向量，实现边缘、角点检测和不同分辨率上的特征提取等。

尺度空间方法将传统的单尺度图像信息处理技术纳入尺度不断变化的动态分析框架中，更容易获取图像的本质特征。尺度空间中各尺度图像的模糊程度逐渐变大，能够模拟人在距离目标由近到远时目标在视网膜上的形成过程。

尺度空间满足视觉不变性。该不变性的视觉解释如下：当我们用眼睛观察物体时，

一方面当物体所处背景的光照条件变化时，视网膜感知图像的亮度水平和对比度是不同的，因此要求尺度空间算子对图像的分析不受图像的灰度水平和对比度变化的影响，即满足灰度不变性和对比度不变性。

另一方面，相对于某一固定坐标系，当观察者和物体之间的相对位置变化时，视网膜所感知的图像的位置、大小、角度和形状是不同的，因此要求尺度空间算子对图像的分析和图像的位置、大小、角度以及仿射变换无关，即满足平移不变性、尺度不变性、欧几里德不变性以及仿射不变性。

尺度空间的表示:

2.1 多分辨率图像金字塔

在早期图像的多尺度通常使用图像金字塔表示形式。图像金字塔是同一图像在不同的分辨率下得到的一组结果，其生成过程一般包括两个步骤：

对原始图像进行平滑
对处理后的图像进行降采样（通常是水平、垂直方向的1/2）,降采样后得到一系列不断尺寸缩小的图像。显然，一个传统的金字塔中，每一层的图像是其上一层图像长、高的各一半。多分辨率的图像金字塔虽然生成简单，但其本质是降采样，图像的局部特征则难以保持，也就是无法保持特征的尺度不变性。

2.2 高斯尺度空间

我们还可以通过图像的模糊程度来模拟人在距离物体由远到近时物体在视网膜上成像过程，距离物体越近其尺寸越大图像也越模糊，这就是高斯尺度空间，使用不同的参数模糊图像（分辨率不变），是尺度空间的另一种表现形式。
我们知道图像和高斯函数进行卷积运算能够对图像进行模糊，使用不同的“高斯核”可得到不同模糊程度的图像。

SIFT算法是在不同的尺度空间上查找关键点，而尺度空间的获取需要使用高斯模糊来实现，Lindeberg等人已证明高斯卷积核是实现尺度变换的唯一变换核，并且是唯一的线性核。本节先介绍高斯模糊算法。

高斯模糊算法

二维高斯函数,

即二维正态分布,高斯模糊是一种图像滤波器，它使用正态分布(高斯函数)计算模糊模板，并使用该模板与原图像做卷积运算，达到模糊图像的目的。

N维空间正态分布方程为：

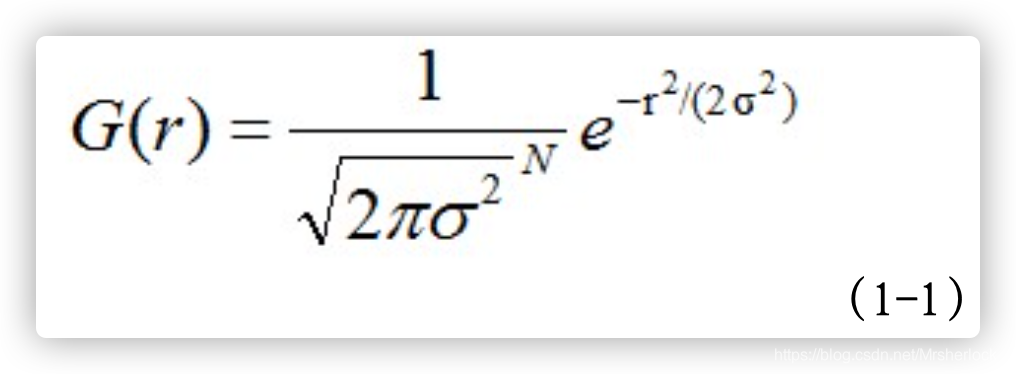
其中，σ是正态分布的标准差， σ值越大，图像越模糊(平滑)。r为模糊半径，模糊半径是指模板元素到模板中心的距离。如二维模板大小为m*n，则模板上的元素(x,y)对应的高斯计算公式为：

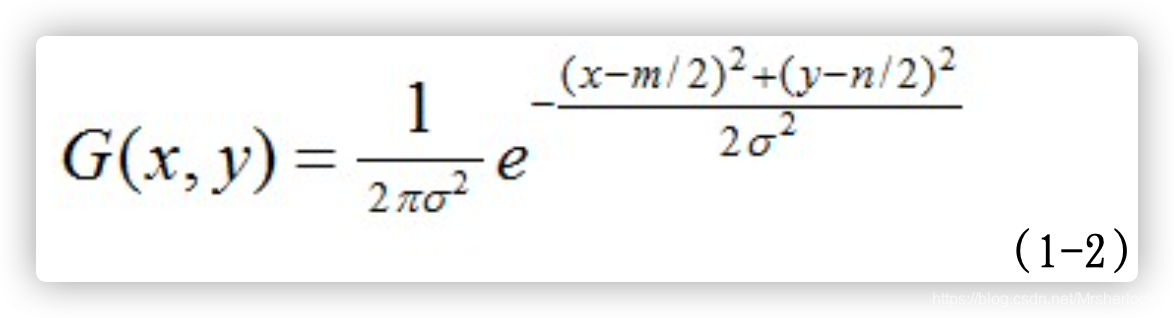
在二维空间中，这个公式生成的曲面的等高线是从中心开始呈正态分布的同心圆，如图2.1所示。分布不为零的像素组成的卷积矩阵与原始图像做变换。每个像素的值都是周围相邻像素值的加权平均。原始像素的值有最大的高斯分布值，所以有最大的权重，相邻像素随着距离原始像素越来越远，其权重也越来越小。这样进行模糊处理比其它的均衡模糊滤波器更高地保留了边缘效果。

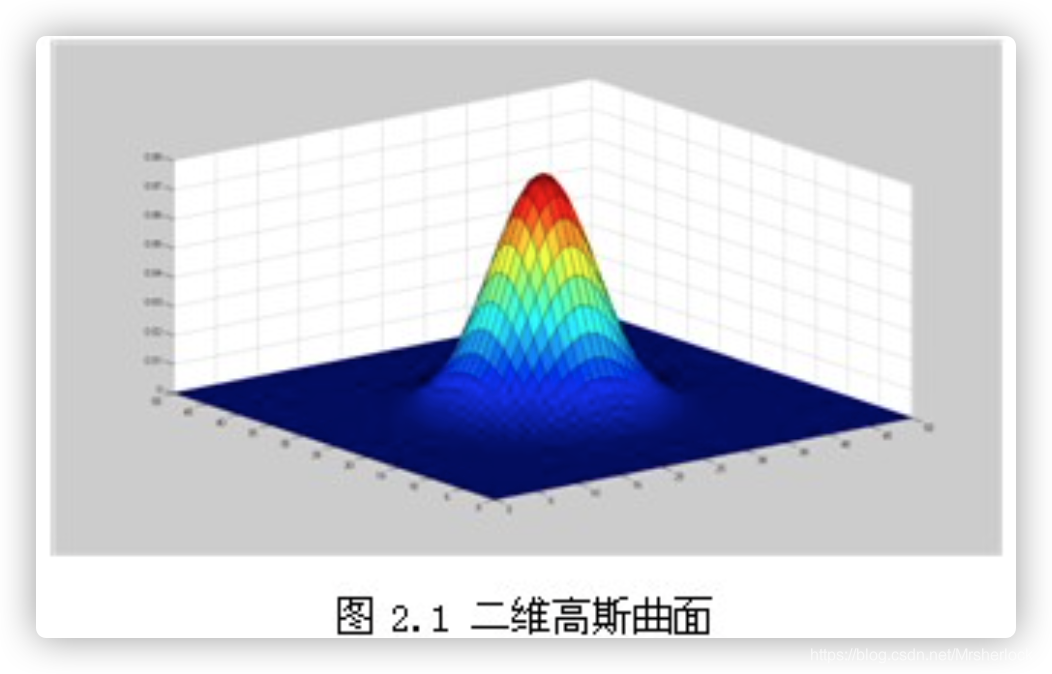
理论上来讲，图像中每点的分布都不为零，这也就是说每个像素的计算都需要包含整幅图像。在实际应用中，在计算高斯函数的离散近似时，在大概3σ距离之外的像素都可以看作不起作用，这些像素的计算也就可以忽略。通常，图像处理程序只需要计算(6σ+1)x(6σ+1) 像素的矩阵就可以保证相关像素影响。

图像的二维高斯模糊

根据σ的值，计算出高斯模板矩阵的大小( (6σ+1)x(6σ+1) )，使用公式: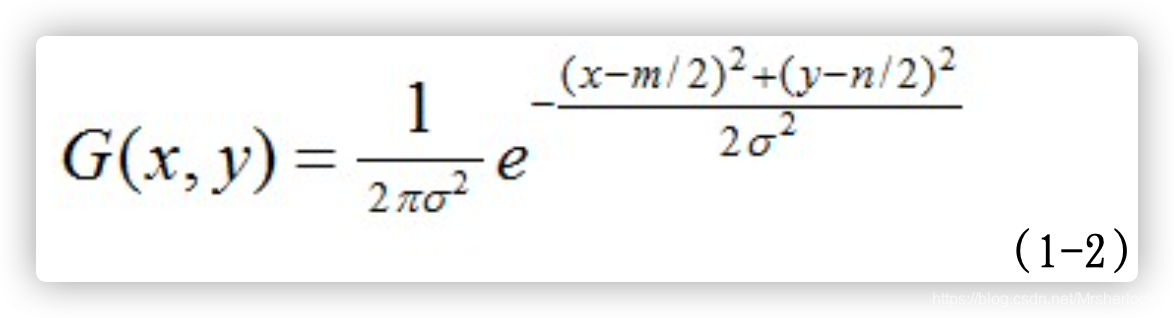

计算高斯模板矩阵的值，为了确保模板矩阵中的元素在[0,1]之间，需将模板矩阵归一化。然后与原图像做卷积，即可获得原图像的平滑(高斯模糊)图像。

5*5的高斯模板如表2.1所示。

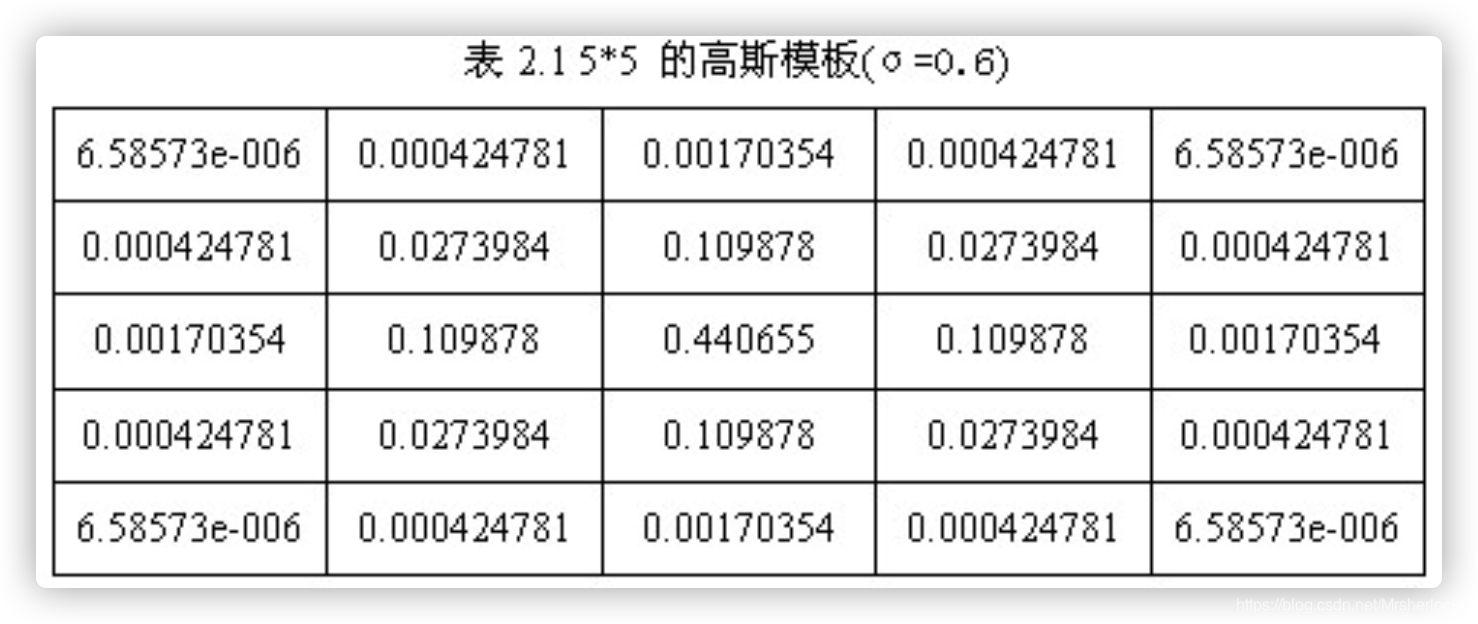
下图是5*5的高斯模板卷积计算示意图。高斯模板是中心对称的。

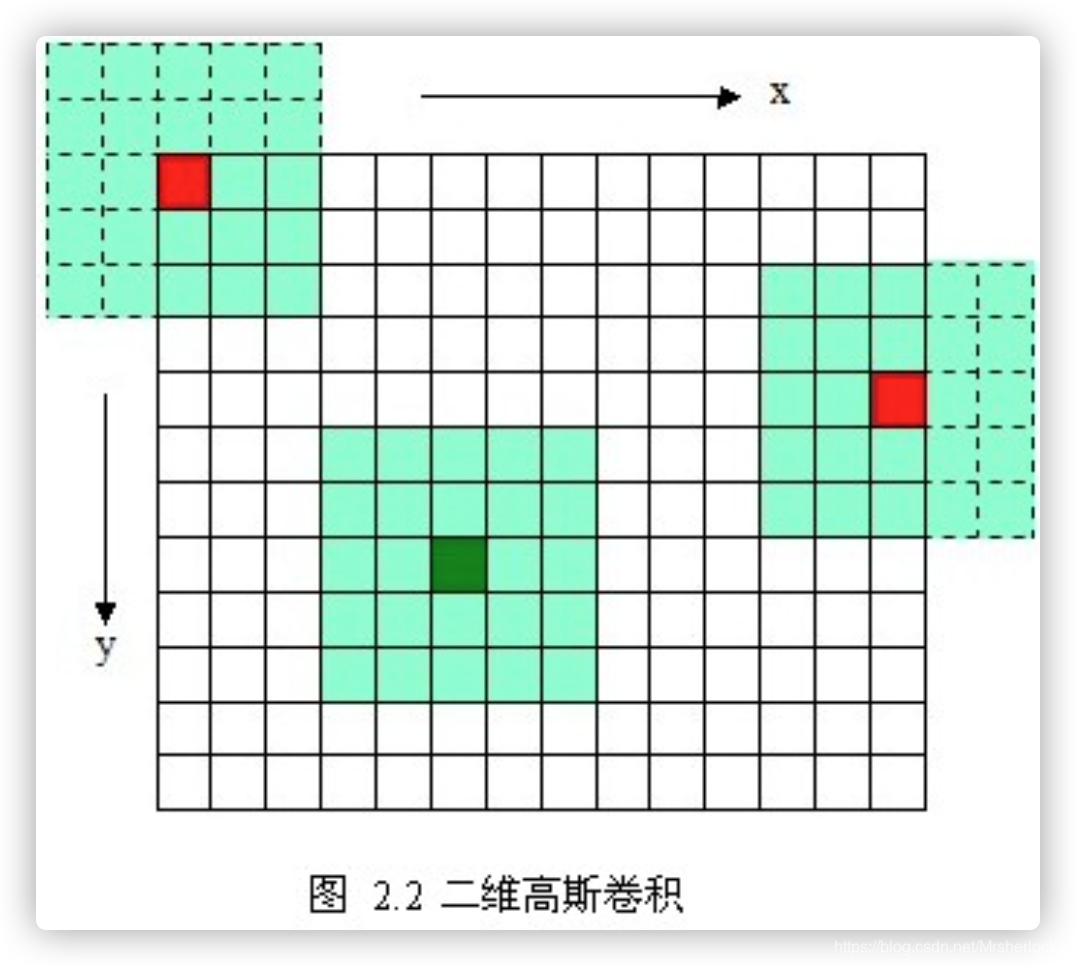
分离高斯模糊

如图2.3所示，使用二维的高斯模板达到了模糊图像的目的，但是会因模板矩阵的关系而造成边缘图像缺失(图2.3 b,c)， σ越大，缺失像素越多,丢弃模板会造成黑边(图2.3 d)。

更重要的是当σ变大时，高斯模板(高斯核)和卷积运算量将大幅度提高。

根据高斯函数的可分离性，可对二维高斯模糊函数进行改进。

高斯函数的可分离性是指使用二维矩阵变换得到的效果也可以通过在水平方向进行一维高斯矩阵变换加上竖直方向的一维高斯矩阵变换得到。

从计算的角度来看，这是一项有用的特性，因为这样只需要次计算，而二维不可分的矩阵则需要次计算，其中，m,n为高斯矩阵的维数，M,N为二维图像的维数。

另外，两次一维的高斯卷积将消除二维高斯矩阵所产生的边缘。

(关于消除边缘的论述如下图2.4所示，对用模板矩阵超出边界的部分——虚线框，将不做卷积计算。如图2.4中x方向的第一个模板1*5，将退化成1*3的模板，只在图像之内的部分做卷积。)

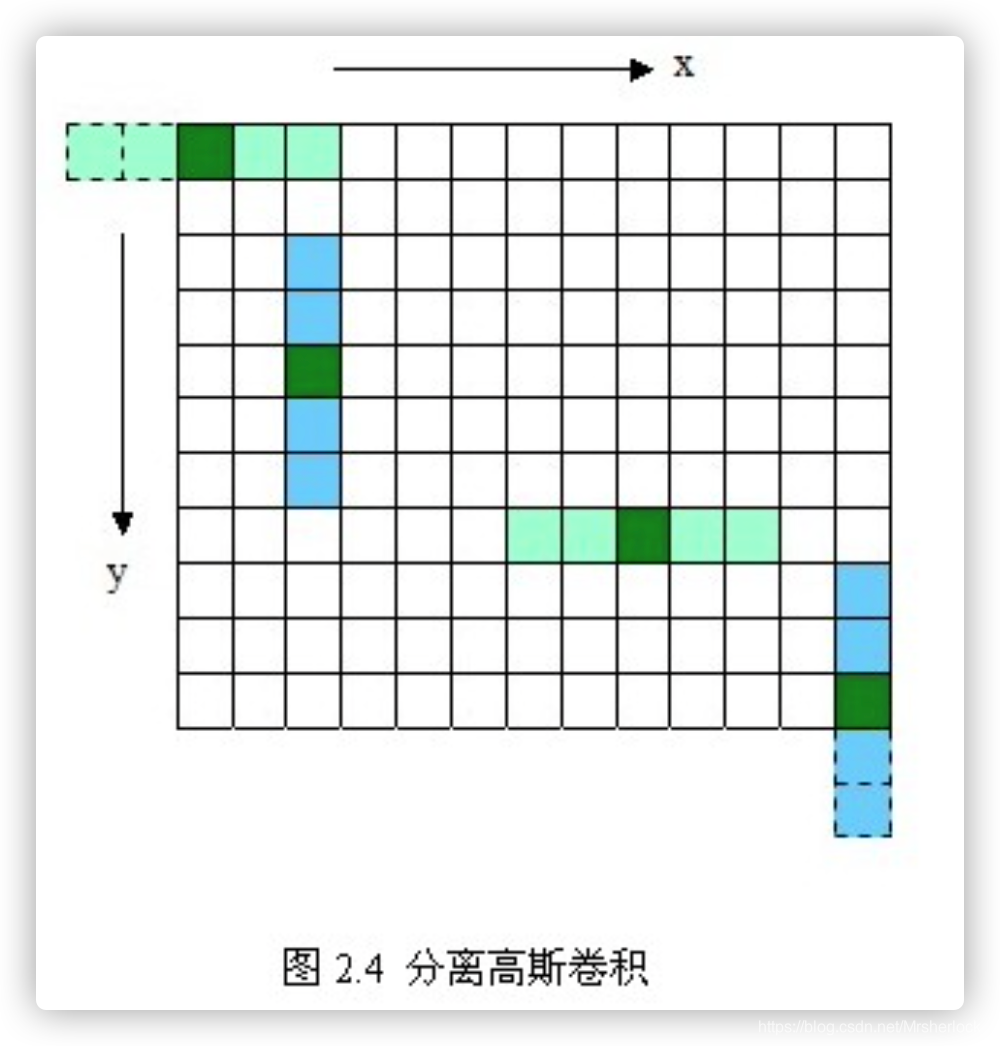
高斯金字塔的构建

尺度空间在实现时, 使用高斯金字塔表示，高斯金字塔的构建分为两部分：

1.对图像做不同尺度的高斯模糊；

2.对图像做降采样(隔点采样)。

图像的金字塔模型是指，将原始图像不断降阶采样，得到一系列大小不一的图像，由大到小，从下到上构成的塔状模型。原图像为金子塔的第一层，每次降采样所得到的新图像为金字塔的一层(每层一张图像)，每个金字塔共n层。金字塔的层数根据图像的原始大小和塔顶图像的大小共同决定，其计算公式如下：

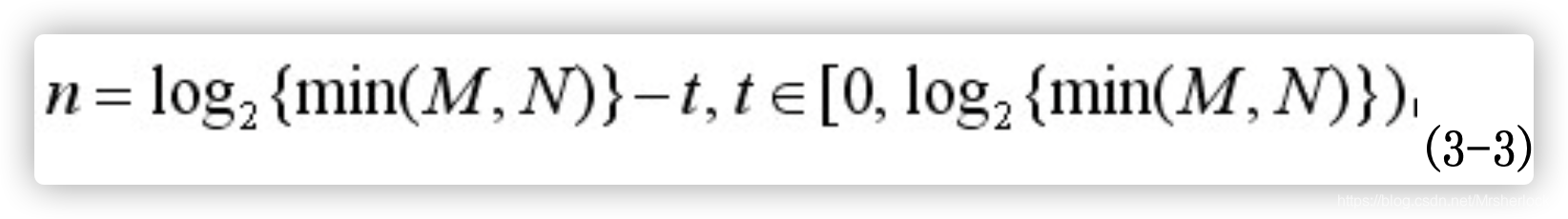
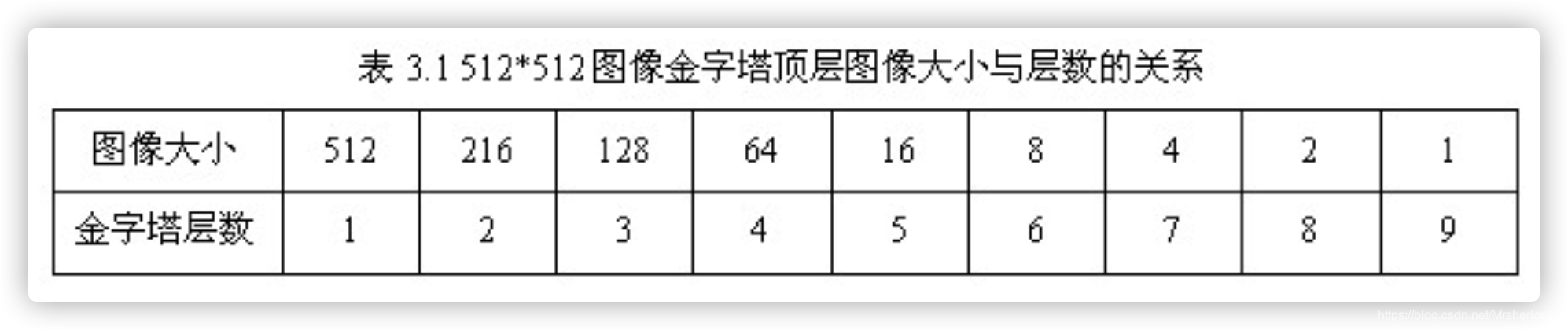
其中M，N为原图像的大小,t为塔顶图像的最小维数的对数值。如，对于大小为512*512的图像，金字塔上各层图像的大小如表3.1所示，当塔顶图像为4*4时，n=7，当塔顶图像为2*2时，n=8。

高斯金字塔模型:

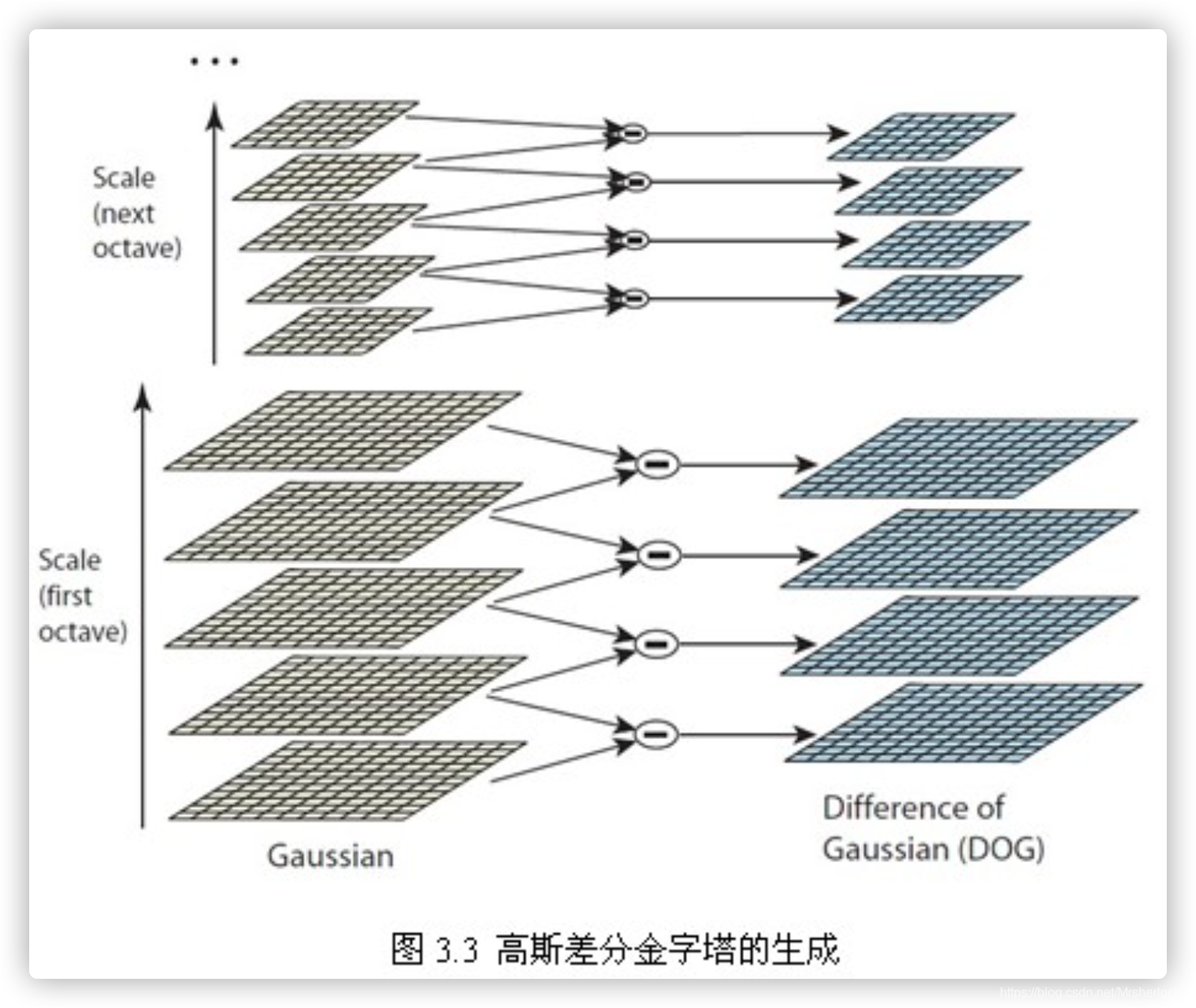
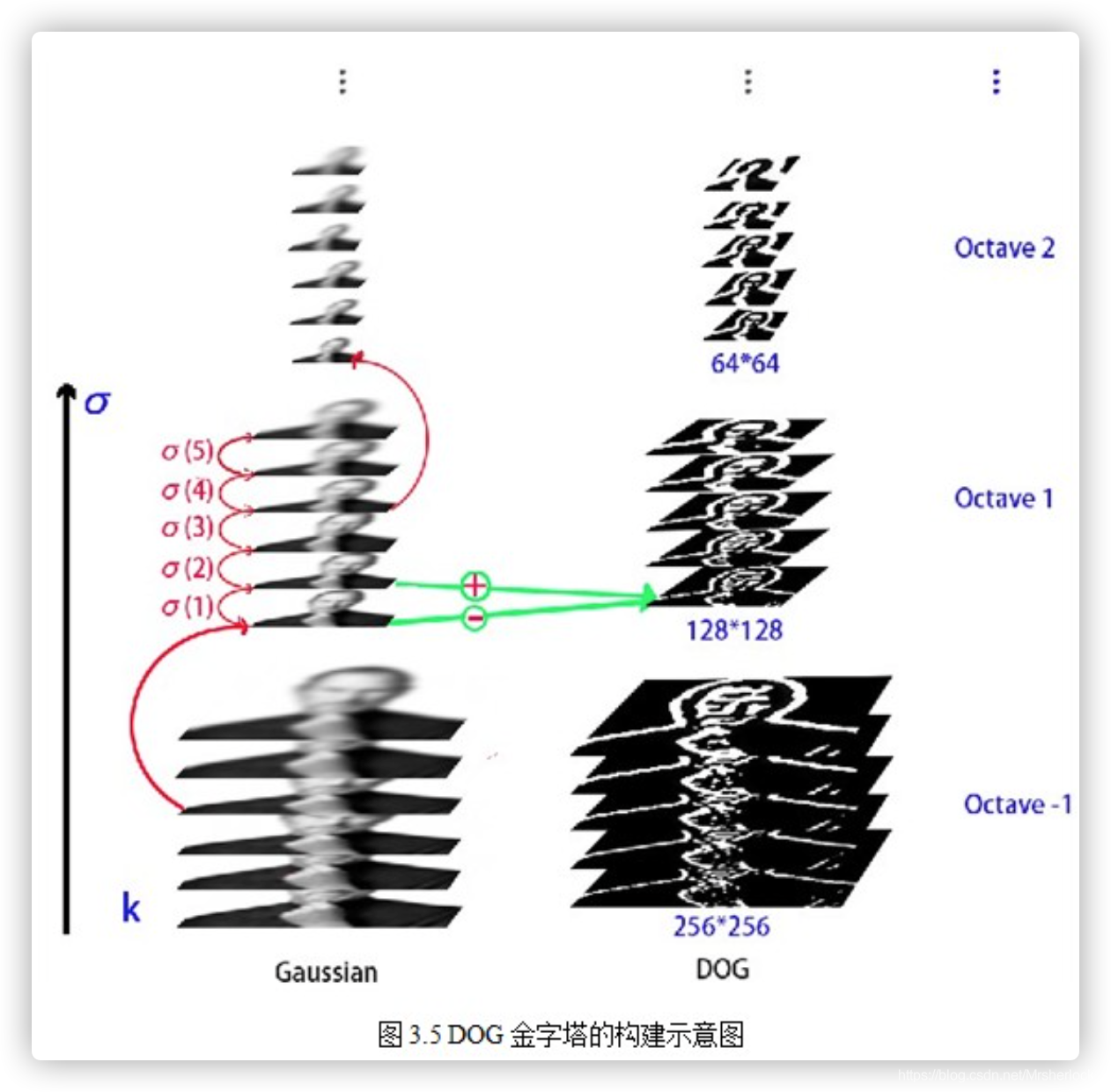
为了让尺度体现其连续性，高斯金字塔在简单降采样的基础上加上了高斯滤波。如图3.1所示，将图像金字塔每层的一张图像使用不同参数做高斯模糊，使得金字塔的每层含有多张高斯模糊图像，将金字塔每层多张图像合称为一组(Octave)，金字塔每层只有一组图像，组数和金字塔层数相等，使用公式(3-3)计算，每组含有多张(也叫层Interval)图像。另外，降采样时，高斯金字塔上一组图像的初始图像(底层图像)是由前一组图像的倒数第三张图像隔点采样得到的。

注：由于组内的多张图像按层次叠放，因此组内的多张图像也称做多层，为避免与金字塔层的概念混淆，本文以下内容中，若不特别说明是金字塔层数，层一般指组内各层图像。

注：如下面马上提到的，为了在每组中检测S个尺度的极值点，则DOG金字塔每组需S+2层图像，而DOG金字塔由高斯金字塔相邻两层相减得到，则高斯金字塔每组需S+3层图像，实际计算时S在3到5之间。取S=3时，假定高斯金字塔存储索引如下：

第0组(即第-1组)： 0 1 2 3 4 5

第1组： 6 7 8 9 10 11

第2组：？

则第2组第一张图片根据第一组中索引为9的图片降采样得到，其它类似。

高斯差分金字塔DOG

2002年Mikolajczyk在详细的实验比较中发现尺度归一化的高斯拉普拉斯函数的极大值和极小值, 同其它的特征提取函数，例如：梯度，Hessian或Harris角特征比较，能够产生最稳定的图像特征。

而Lindeberg早在1994年就发现高斯差分函数（Difference of Gaussian ，简称DOG算子）与尺度归一化的高斯拉普拉斯函数非常近似。其中和的关系可以从如下公式推导得到：

,利用差分近似代替微分，则有：

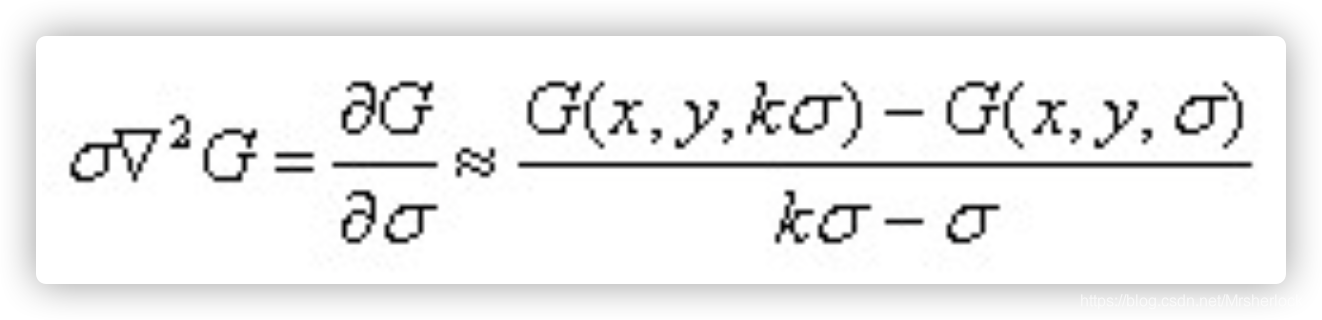
综上所述:

其中, k-1是个常数，并不影响极值点位置的求取。

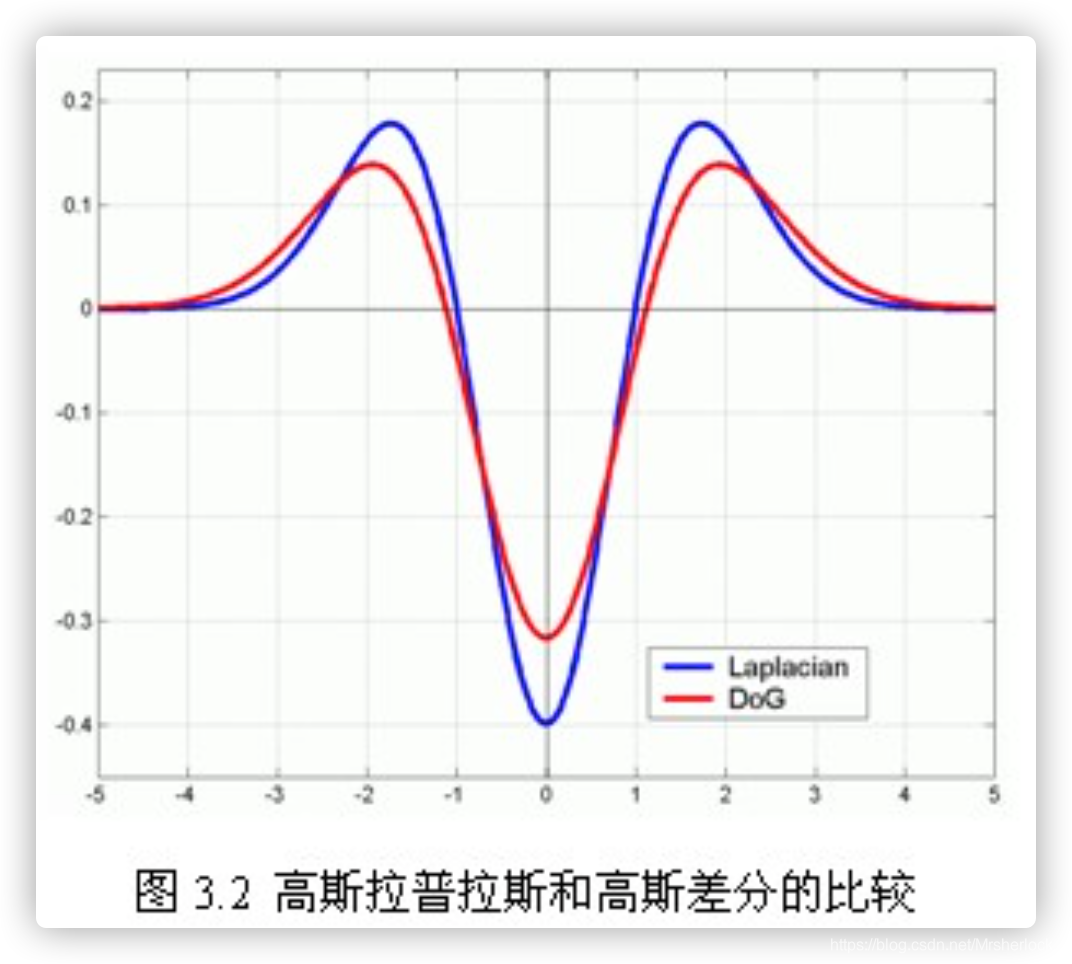
如图3.2所示，红色曲线表示的是高斯差分算子，而蓝色曲线表示的是高斯拉普拉斯算子。Lowe使用更高效的高斯差分算子代替拉普拉斯算子进行极值检测，如下：

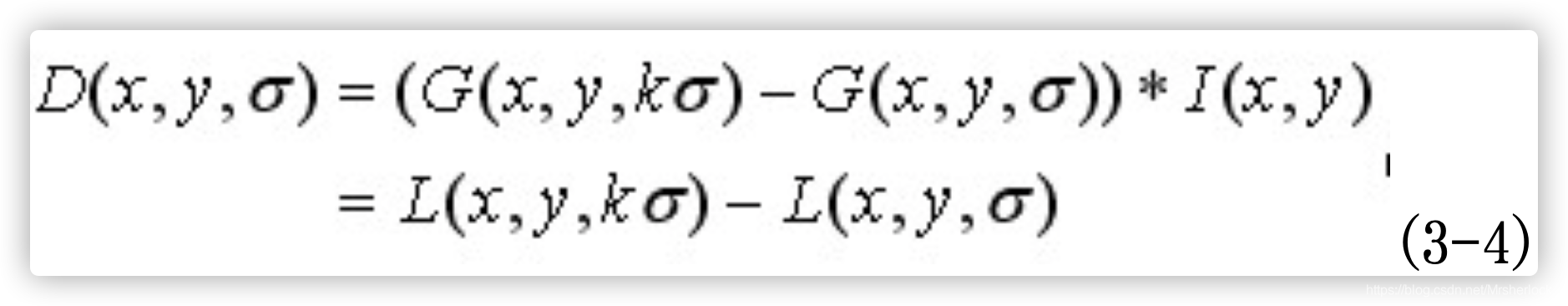
在实际计算时，使用高斯金字塔每组中相邻上下两层图像相减，得到高斯差分图像，如图3.3所示，进行极值检测。

3.尺度空间参数计算和极值点初步探查

关键点的初步探查

关键点是由DOG空间的局部极值点组成的，关键点的初步探查是通过同一组内各DoG相邻两层图像之间比较完成的。为了寻找DoG函数的极值点，每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小。如图3.4所示，中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。

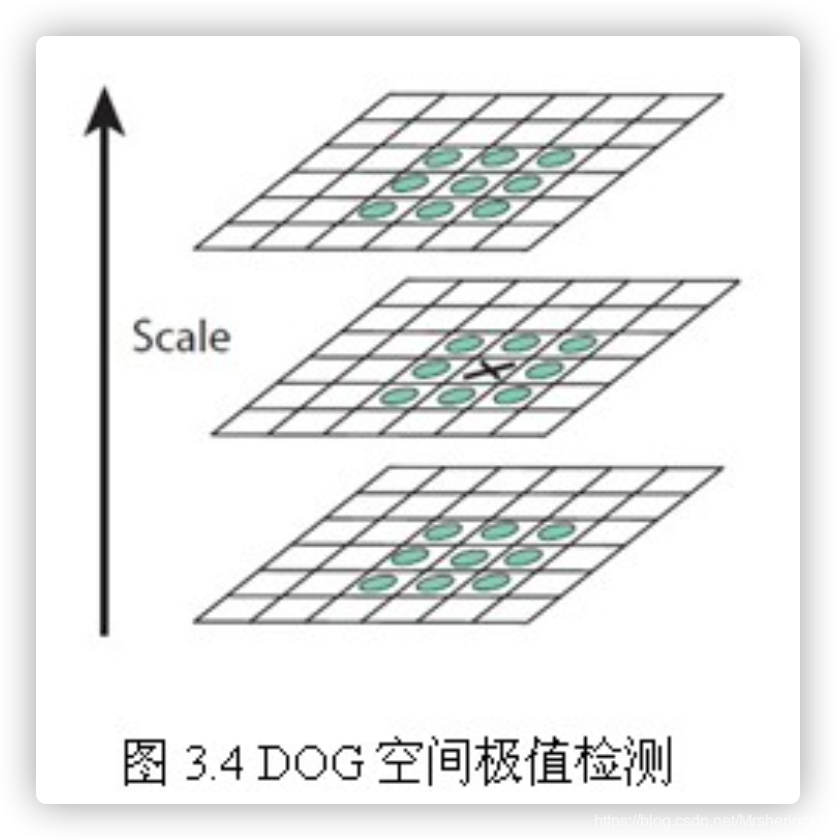
由于要在相邻尺度进行比较，如图3.3右侧每组含4层的高斯差分金子塔，只能在中间两层中进行两个尺度的极值点检测，其它尺度则只能在不同组中进行。

为了在每组中检测S个尺度的极值点，则DOG金字塔每组需S+2层图像，而DOG金字塔由高斯金字塔相邻两层相减得到，则高斯金字塔每组需S+3层图像，实际计算时S在3到5之间。

当然这样产生的极值点并不全都是稳定的特征点，因为某些极值点响应较弱，而且DOG算子会产生较强的边缘响应。

构建尺度空间需确定的参数:

σ—尺度空间坐标

O—组(octave)数

S— 组内层数, 实际计算往往取3-5之间

计算σ—尺度空间坐标:

在上述尺度空间中，O和S，σ 的关系如下：

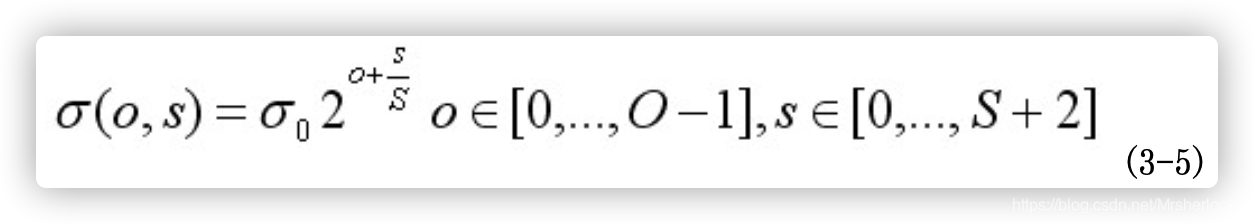
其中σ 0是基准层尺度，o为组octave的索引，s为组内层的索引。关键点的尺度坐标σ 就是按关键点所在的组和组内的层，利用公式(3-5)计算而来。

在最开始建立高斯金字塔时，要预先模糊输入图像来作为第0个组的第0层的图像，这时相当于丢弃了最高的空域的采样率。因此通常的做法是先将图像的尺度扩大一倍来生成第-1组。我们假定初始的输入图像为了抗击混淆现象，已经对其进行的高斯模糊，如果输入图像的尺寸用双线性插值扩大一倍，那么相当于

取式(3-4)中的k为组内总层数的倒数，即 :

(3-6)

在构建高斯金字塔时，组内每层的尺度坐标按如下公式计算：

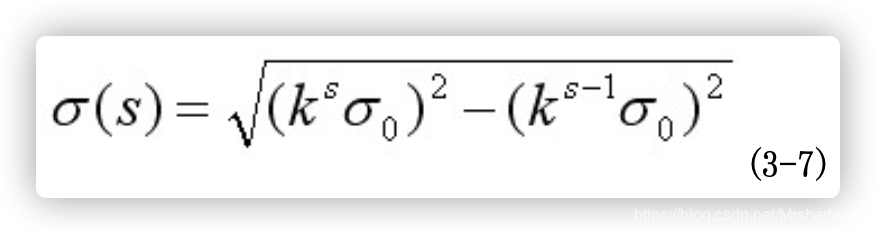
其中初始尺度，作者lowe取，s为组内的层索引，不同组相同层的组内尺度坐标相同。

组内下一层图像是由前一层图像按进行高斯模糊所得。

式(3-7)用于一次生成组内不同尺度的高斯图像，而在计算组内某一层图像的尺度时，直接使用如下公式进行计算：

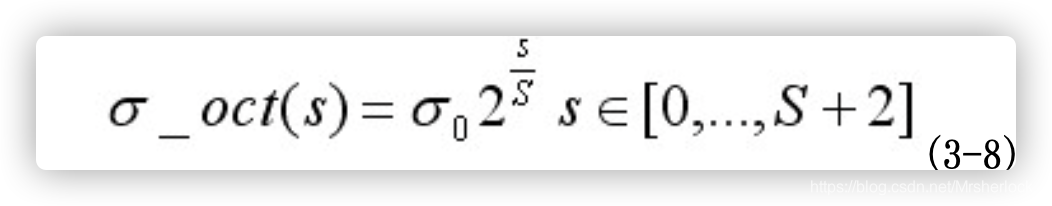
该组内尺度在方向分配和特征描述时确定采样窗口的大小。

上式(3-4)可记为:

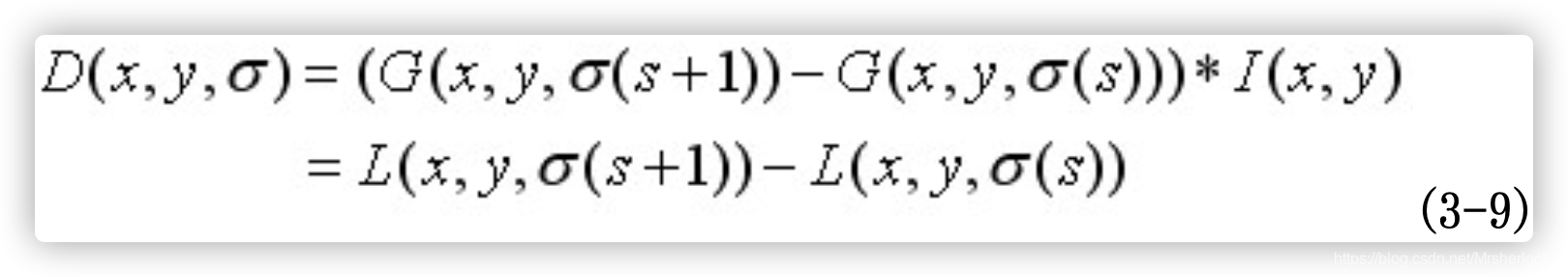
图3.5为构建DOG金字塔的示意图，原图采用128*128的jobs图像，扩大一倍后构建金字塔。

4. 关键点的精确定位

以上方法检测到的极值点是离散空间的极值点，以下通过拟合三维二次函数D来精确确定关键点的位置和尺度，同时去除低对比度的关键点和不稳定的边缘响应点(因为DoG算子会产生较强的边缘响应)，以增强匹配稳定性、提高抗噪声能力。

4.1获取关键点精准位置

离散空间的极值点并不是真正的极值点，图4.1显示了二维函数离散空间得到的极值点与连续空间极值点的差别。利用已知的离散空间点插值得到的连续空间极值点的方法叫做子像素插值（Sub-pixel Interpolation）。

为了提高关键点的稳定性，需要对尺度空间DoG函数进行曲线拟合。利用DoG函数在尺度空间的Taylor展开式(拟合函数)为：

其中，。

求导并让方程等于零，可以得到极值点的偏移量为：(4-2)

极值点带入D(X)方程中,得：(4-3),

其中, 代表相对插值中心的偏移量，当它在任一维度上的偏移量大于0.5时（即x或y或σ ），意味着插值中心已经偏移到它的邻近点上，所以必须改变当前关键点的位置。同时在新的位置上反复插值直到收敛；也有可能超出所设定的迭代次数或者超出图像边界的范围，此时这样的点应该删除，在Lowe中进行了5次迭代。

另外，过小的点易受噪声的干扰而变得不稳定，所以将小于某个经验值(Lowe论文中使用0.03，Rob Hess等人实现时使用0.04/S)的极值点删除。

同时，在此过程中获取特征点的精确位置(原位置加上拟合的偏移量)以及尺度( )。

4.2 消除边缘响应

一个定义不好的高斯差分算子的极值在横跨边缘的地方有较大的主曲率，而在垂直边缘的方向有较小的主曲率。

DOG算子会产生较强的边缘响应，需要剔除不稳定的边缘响应点。获取特征点处的Hessian矩阵，主曲率通过一个2x2 的Hessian矩阵H求出：

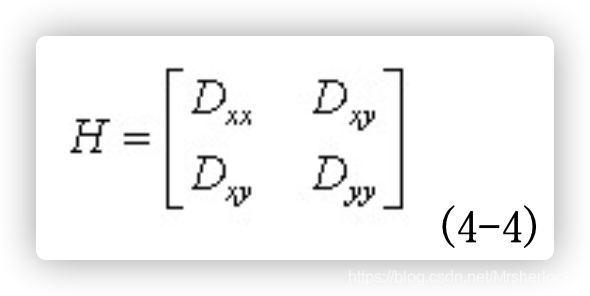
H的特征值α和β代表x和y方向的梯度，其中Tr表示矩阵的迹trace, det表示矩阵行列式

假设是α较大的特征值，而是β较小的特征值，令，则导数由采样点相邻差估计得到,在下一节中说明。

D的主曲率和H的特征值成正比，令为α最大特征值，β为最小的特征值，则公式的值, 在两个特征值相等时最小，且随着r增大而增大。

r值越大，说明两个特征值的比值越大，即在某一个方向的梯度值越大，而在另一个方向的梯度值越小，而边缘恰恰就是这种情况。所以为了剔除边缘响应点，需要让该比值小于一定的阈值，因此，为了检测主曲率是否在某域值r下，只需检测

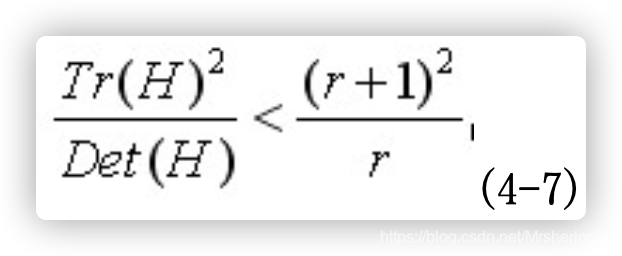
式(4-7)成立时将关键点保留，反之剔除。

在Lowe的文章中，取r＝10。图4.2右侧为消除边缘响应后的关键点分布图。

5. 关键点方向分配(旋转不变性)

根据前四节,已经获得了关键点的位置和σ值

为了使描述符具有旋转不变性，需要利用图像的局部特征为给每一个关键点分配一个基准方向。

使用图像梯度的方法求取局部结构的稳定方向。

对于在DOG金字塔中检测出的关键点，采集其所在高斯金字塔图像3σ邻域窗口内像素的梯度和方向分布特征。

梯度的模值和方向如下：

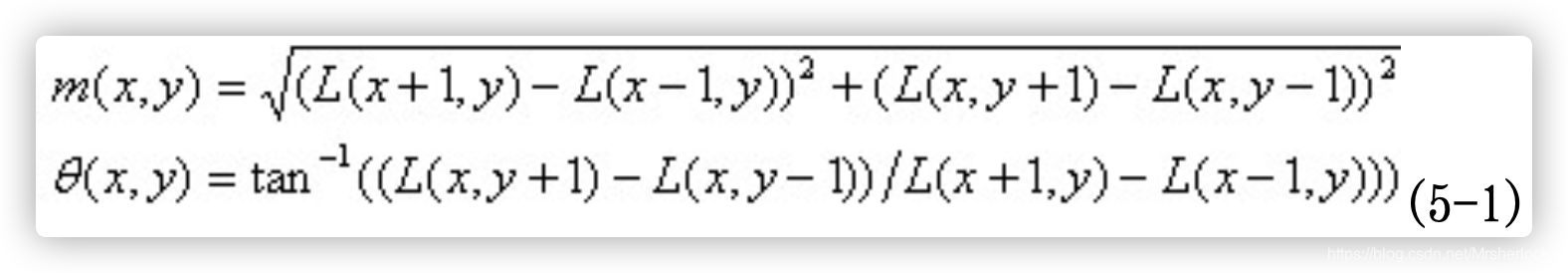
根据上面文章提到的:

计算组内某一层图像的尺度时，直接使用如下公式进行计算：

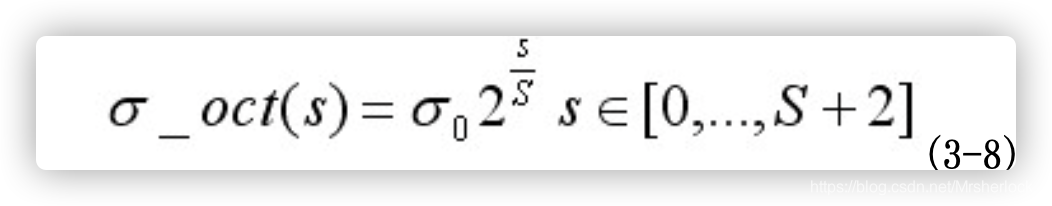
对于式(5-1) L为关键点所在的尺度空间值，按Lowe的建议，梯度的模值m(x,y)按的高斯分布加成,即应*G(x,y,1.5σ);按尺度采样的3σ原则，邻域窗口半径为。

在完成关键点的梯度计算后，使用直方图统计邻域内像素的梯度大小和方向。梯度直方图将0~360度的方向范围分为36个柱(bins)，其中每柱10度。如图5.1所示，直方图的峰值方向代表了关键点的主方向，(为简化，图中只画了八个方向的直方图)。

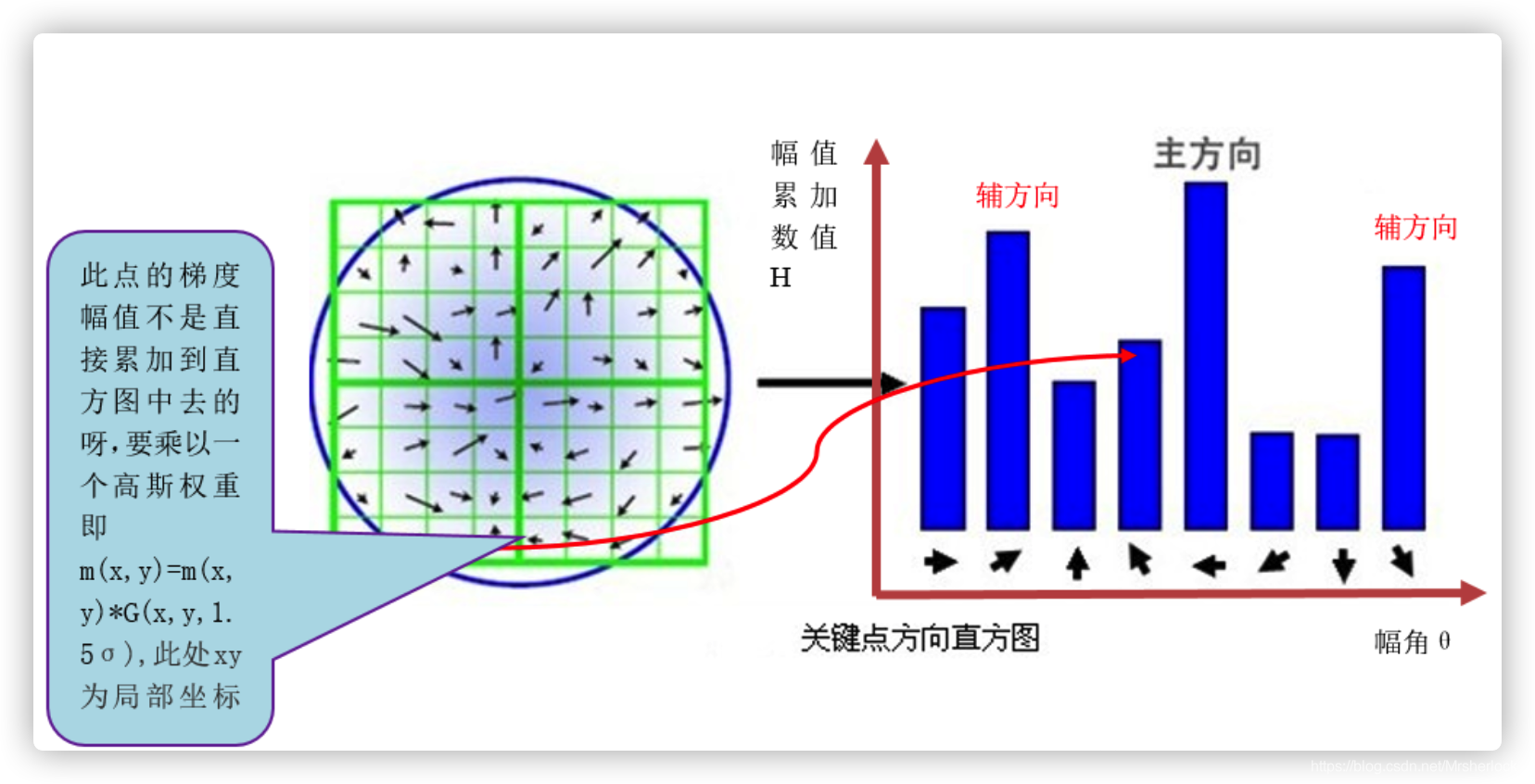
方向直方图的峰值则代表了该特征点处邻域梯度的方向，以直方图中最大值作为该关键点的主方向。为了增强匹配的鲁棒性，只保留峰值大于主方向峰值80％的方向作为该关键点的辅方向。

因此，对于同一梯度值的多个峰值的关键点位置，在相同位置和尺度将会有多个关键点被创建但方向不同。仅有15％的关键点被赋予多个方向，但可以明显的提高关键点匹配的稳定性。实际编程实现中，就是把该关键点复制成多份关键点，并将方向值分别赋给这些复制后的关键点，并且，离散的梯度方向直方图要进行插值拟合处理，来求得更精确的方向角度值，检测结果如图5.2所示。

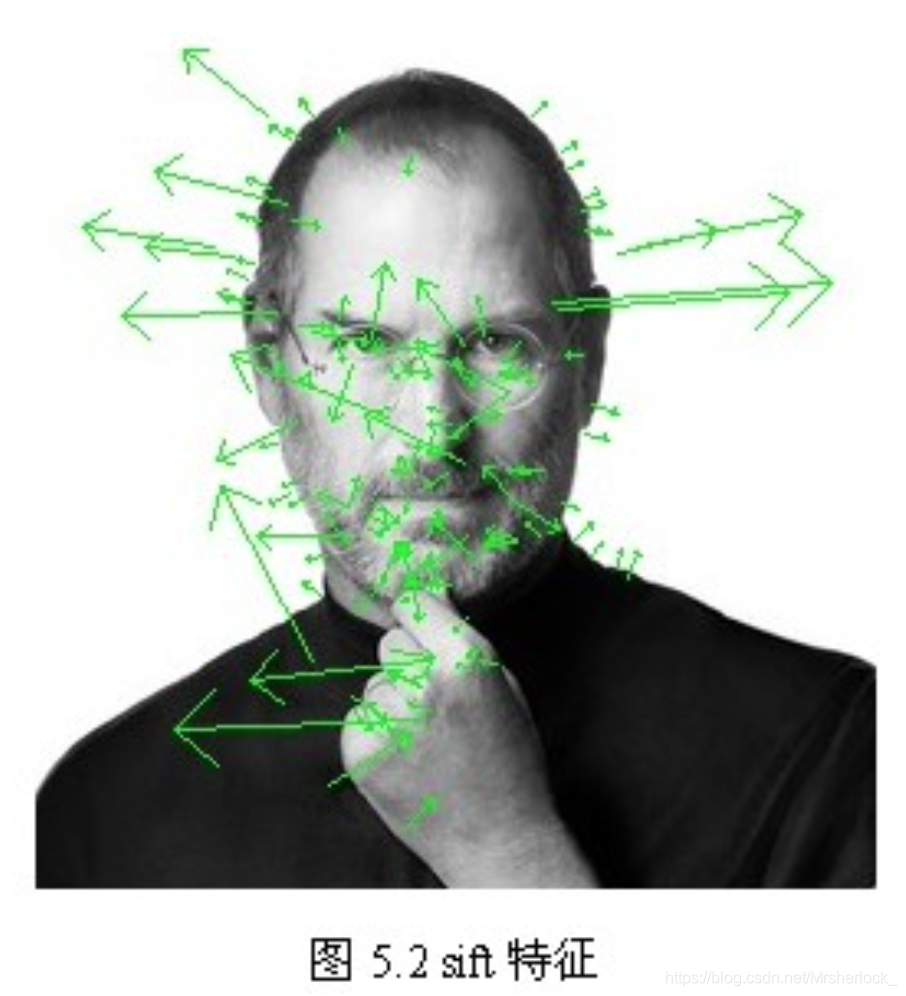
至此，将检测出的含有( 位置x,y、尺度σ_oct和方向) 的关键点即是该图像的SIFT特征点。

6. 关键点特征描述(重难点)

通过以上步骤，对于每一个关键点，拥有三个信息：位置、尺度以及方向。

接下来就是为每个关键点建立一个描述符/描述子，用一组向量将这个关键点描述出来，使其不随各种变化而改变，比如光照变化、视角变化等等。

这个描述子不但包括关键点，也包含关键点周围对其有贡献的像素点，并且描述符应该有较高的独特性，以便于提高特征点正确匹配的概率。

SIFT描述子是关键点邻域高斯图像梯度统计结果的一种表示。通过对关键点周围图像区域分块，计算块内梯度直方图，生成具有独特性的向量，这个向量是该区域图像信息的一种抽象，具有唯一性。

Lowe建议描述子使用在关键点尺度空间内4*4的窗口中, 计算的每个窗口中的8个方向的梯度信息，共4*4*8=128维向量表征。

表示步骤如下：

1. 确定计算描述子所需的图像区域

特征描述子与特征点所在的尺度有关，因此，对梯度的求取应在特征点对应的高斯图像上进行。

将关键点附近的邻域划分为d*d(Lowe建议d=4)个子区域，每个子区域做为一个种子点，每个种子点有8个方向。

⚠️这里不是说分配了(d=4)4x4=16个像素,而是说分配了16个子区域,每个子区域范围如下:

每个子区域的大小与关键点方向分配时相同，即每个区域有个子像素，每个子区域分配边长为的矩形区域进行采样(个子像素实际用边长为的矩形区域即可包含，但由式(3-8)，不大，为了简化计算取其边长为并且采样点宜多不宜少)。

考虑到实际计算时，需要采用双线性插值，所需图像窗口边长为

在考虑到旋转因素(方便下一步将坐标轴旋转到关键点的方向)，如下图6.1所示，实际计算中, 1个子区域所需的图像区域半径为：

计算结果四舍五入取整。

这里因方便旋转, 子区域不再是标准的矩形而是一个半径为radius的圆所包含的下标是整数的像素.

一个关键点一般来说d=4,有16个半径为radius的圆形子区域, 即16个种子点,每个种子点包含了8个特征,即一个关键点包含了128个特征信息.

绿色圆表示要计算的区域,只计算整数位置的像素,所以黑色方块区域是实际计算的像素位置

2. 将坐标轴旋转为关键点的方向，以确保旋转不变性，如6.2所示。

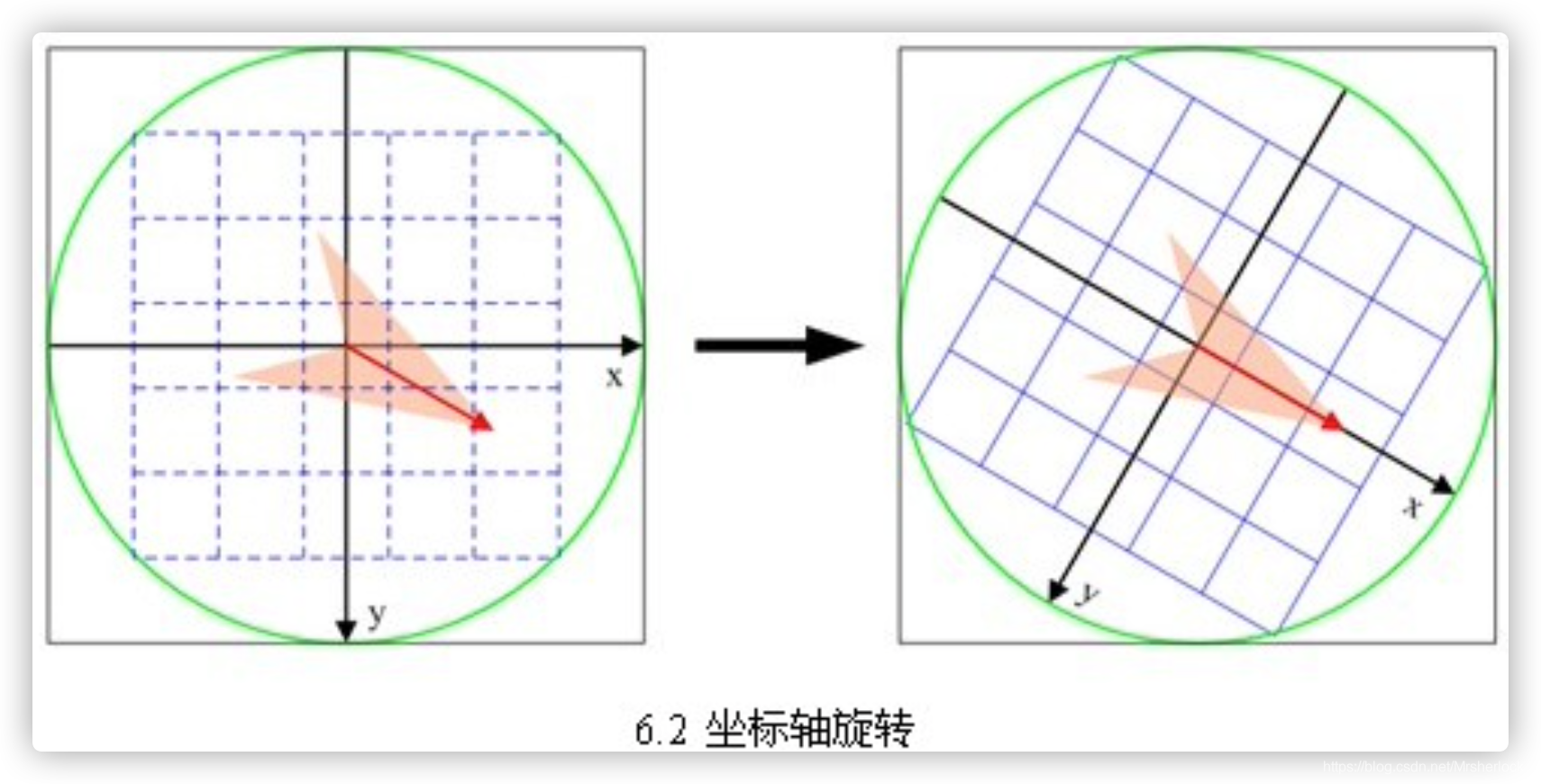
旋转后采样点的新坐标为：(即1个子区域内所覆盖的像素点的新坐标)

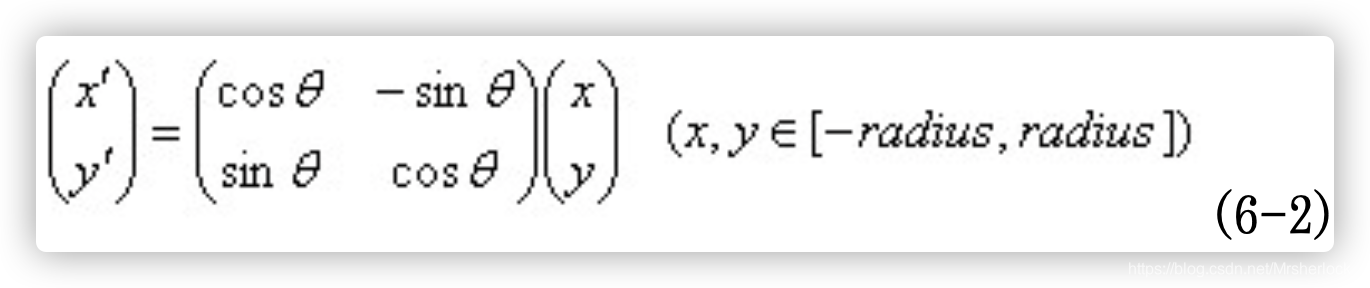
3. 将采样点分配到对应的子区域内，将子区域内的梯度值分配到8个方向上，计算其权值。

旋转后的采样点坐标在半径为radius的圆内, 被分配到个数是dxd的子区域,一般d=4,

计算影响子区域的采样点的梯度和方向，分配到8个方向上。

旋转后的采样点坐标落在子区域的下标为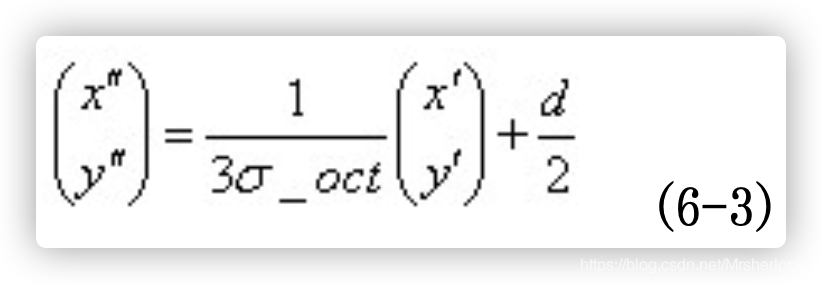

权值计算:

Lowe建议子区域的像素的梯度大小按的高斯加权计算，即

其中a，b为关键点在高斯金字塔图像中的位置坐标。

4. 插值计算每个种子点八个方向的梯度。

种子点是指,每个关键点的子区域作为一个种子点,计算该种子点八个方向的梯度

下图中蓝紫色圆和格子,是为了三线性插值而扩充的,因为旋转后的采样点对应在子区域的坐标,未必会全落在子区域中

且每个绿色格子都占了4个蓝紫色格子的1/4,这个4个蓝紫色格子的梯度值,都属于该绿色格子的统计范围

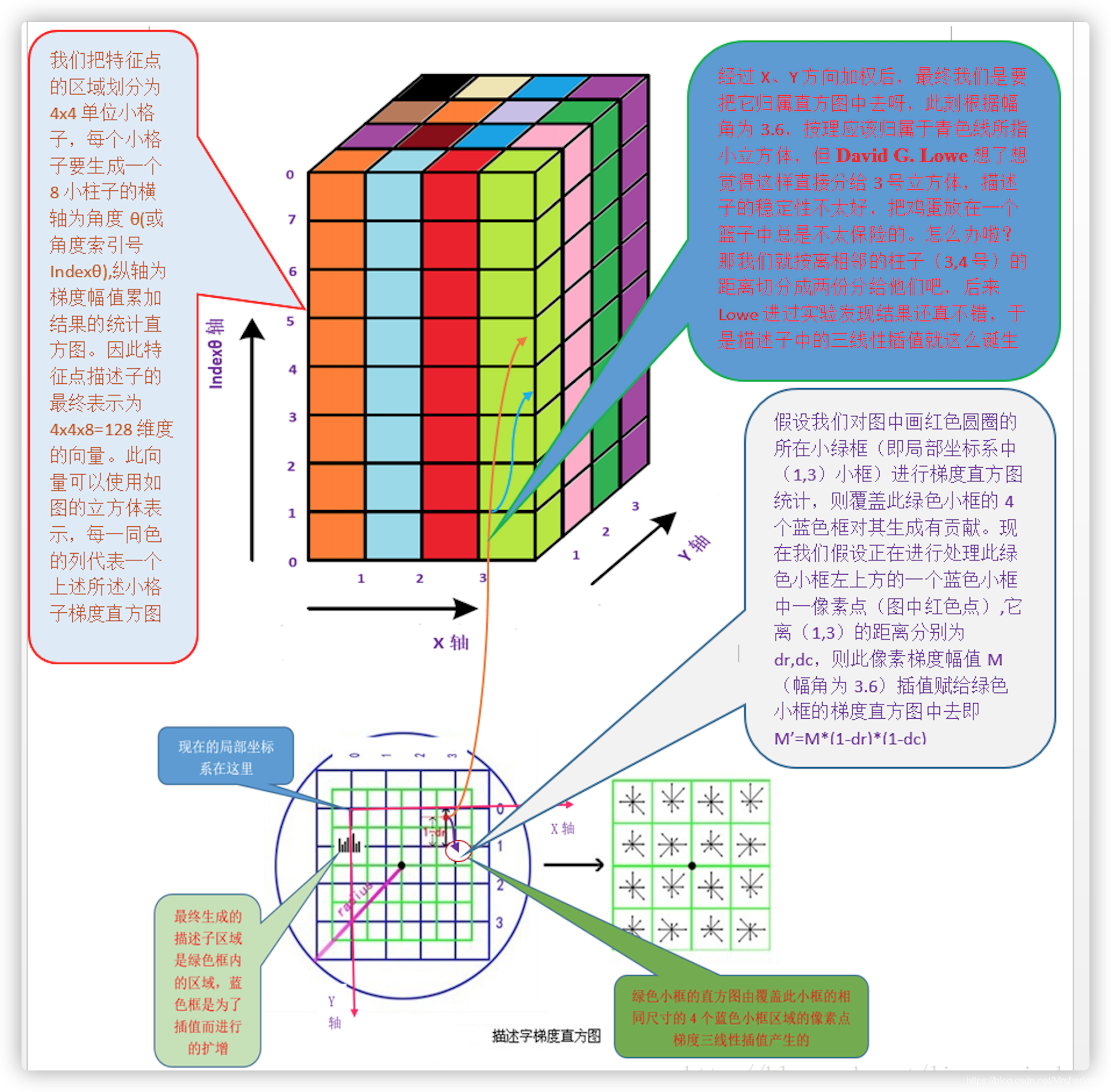
如图6.3所示，将由式(6-3)所得旋转后的采样点在子区域中的下标 (图中蓝色窗口内红色点)线性插值，计算其对每个种子点的贡献。

如图中的红色点，落在第0行和第1行之间，对这两行都有贡献。对第0行第3列种子点的贡献因子为dr，对第1行第3列的贡献因子为1-dr，同理，对邻近两列的贡献因子为dc和1-dc，对邻近两个方向的贡献因子为do和1-do。

则最终累加在每个方向上的梯度大小为：

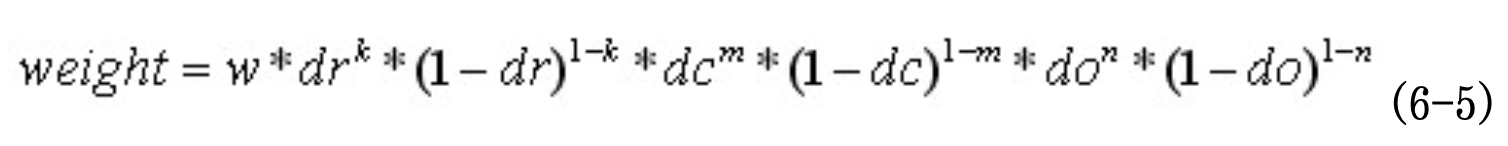其中k，m，n为0或为1。

其中k，m，n

当像素点超出了对要插值区间的四个邻近子区间所在范围时, 为0

当像素点处在对要插值区间的四个邻近子区间之一所在范围时,为1

5. 如上统计的4*4*8=128个梯度信息即为该关键点的特征向量。

特征向量形成后，为了去除光照变化的影响，需要对它们进行归一化处理，对于图像灰度值整体漂移，图像各点的梯度是邻域像素相减得到，所以也能去除。

得到的描述子向量为

归一化后的特征向量为则

6. 描述子向量门限。

非线性光照，相机饱和度变化对造成某些方向的梯度值过大，而对方向的影响微弱。因此设置门限值(向量归一化后，一般取0.2)截断较大的梯度值, 大于0.2的则就令它等于0.2，小于0.2的则保持不变。

然后，再进行一次归一化处理，提高特征的鉴别性。

7. 按特征点的尺度对特征描述向量进行排序。

至此，SIFT特征描述向量生成。

8. SIFT的缺点

SIFT在图像的不变特征提取方面拥有无与伦比的优势，但并不完美，仍然存在：

1. 实时性不高。

2. 有时特征点较少。

3. 对边缘光滑的目标无法准确提取特征点。

等缺点，如下图7.1所示，对模糊的图像和边缘平滑的图像，检测出的特征点过少，对圆更是无能为力。近来不断有人改进，其中最著名的有SURF和CSIFT。

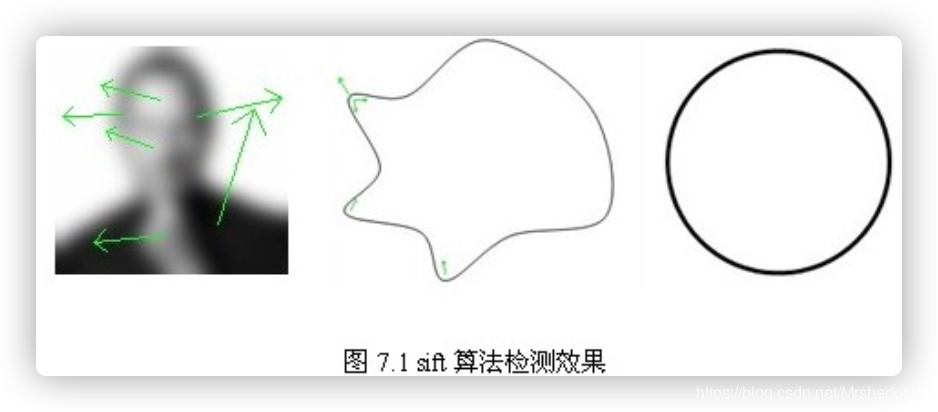
OpenCV3的实现

SURF特征检测

SURF算法原理

1、SURF特征检测的步骤概述

1.尺度空间的极值检测：搜索所有尺度空间上的图像，通过Hessian来识别潜在的对尺度和选择不变的兴趣点, 构造尺度空间

2.特征点过滤并进行精确定位。

3.特征方向赋值：统计特征点圆形邻域内的Harr小波特征:即在60度扇形内，每次将60度扇形区域旋转0.2弧度进行统计，将值最大的那个扇形的方向作为该特征点的主方向。

4.特征点描述：沿着特征点主方向周围的邻域内，取4×4×4个矩形小区域，统计每个小区域的Haar特征，然后每个区域得到一个4维的特征向量。

一个特征点共有64维的特征向量作为SURF特征的描述子。

2、构建Hessian(黑塞矩阵)

构建Hessian矩阵的目的是为了生成图像稳定的边缘点(突变点)，跟Canny、拉普拉斯边缘检测的作用类似，为特征提取做准备。

构建Hessian矩阵的过程对应着SIFT算法中的DoG过程。

黑塞矩阵(Hessian Matrix)是由一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。由德国数学家Ludwin Otto Hessian于19世纪提出。

对于一个图像I(x,y)，其Hessian矩阵如下：

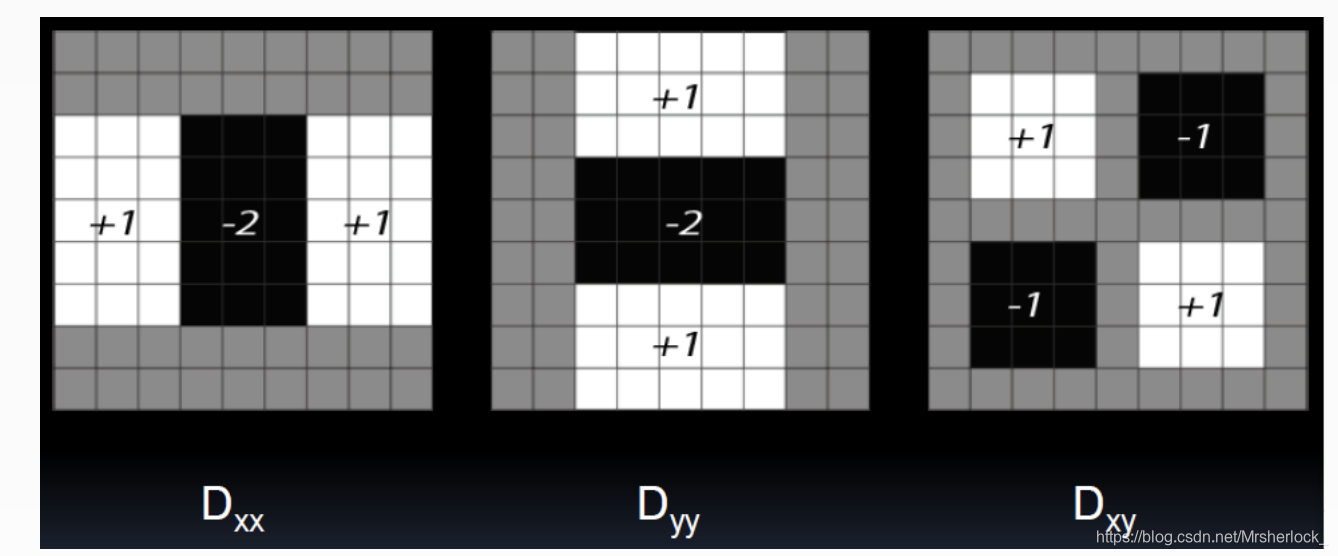
H矩阵的判别式是：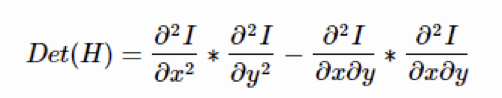

特征点需要具备尺度无关性(即模糊系数无关性), 在构建Hessian矩阵前需要对图像进行高斯滤波，经过滤波后的Hessian矩阵表达式为：

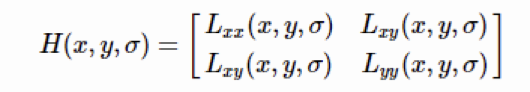
其中(x,y)为像素位置,L(x,y,σ)=G(σ)∗I(x,y),代表着图像的高斯尺度空间，是由图像和不同的高斯卷积G(σ)得到。

理解Hessian矩阵:

在离散数学图像中，一阶导数是相邻像素的灰度差：

二阶导数是对一阶导数的再次做差求导：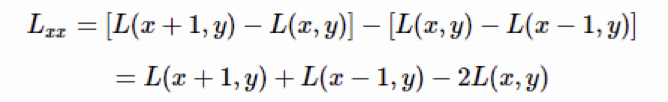

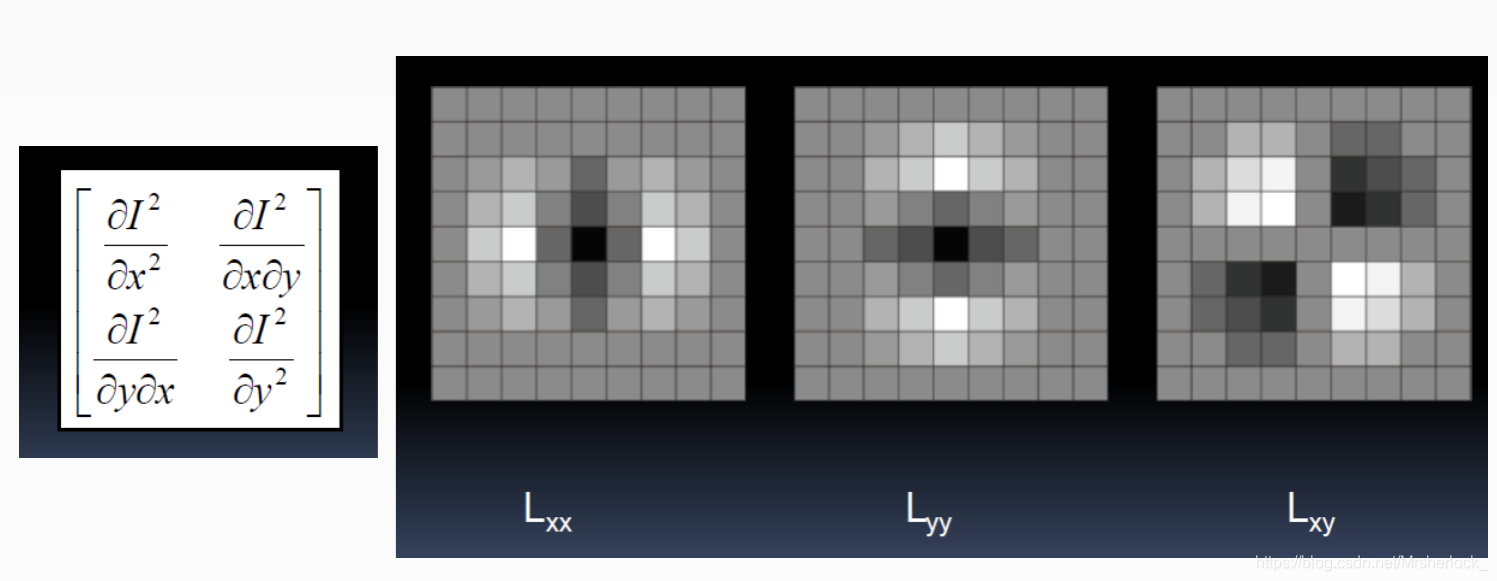
反过来看Hessian矩阵的判别式，其实就是当前点对水平方向二阶偏导数乘以垂直方向二阶偏导数再减去当前水平、垂直二阶偏导的二次方：

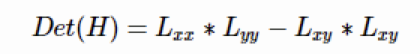
通过这种方法可以为图像中每个像素计算出其H行列式的决定值，并用这个值来判别图像局部特征点。也就是说: 判别式的值是H矩阵的特征值，可以利用判定结果的符号将所有点分类，根据判别式取值正负，来判别该点是或不是极值点。

Hession矩阵判别式中的L是原始图像的高斯卷积，

由于高斯核G服从正太分布，从中心点往外，系数越来越小，为了提高运算速度，SURF算法使用了盒式滤波器来替代高斯滤波器L，所以在Lxy上乘了一个加权系数0.9，该系数是个经验值

目的是为了平衡因使用盒式滤波器近似所带来的误差，则H矩阵判别式可表示为：

由于求Hessian时要先高斯平滑保证尺度无关性，然后求二阶导数，这在离散的像素点是用模板卷积形成的，这两种操作合在一起用一个模板代替就可以了，比如说y方向上的模板如下：

该图的左边即用高斯平滑然后在y方向上求二阶导数的模板，为了加快运算用了近似处理，其处理结果如右图所示，这样就简化了很多。并且右图可以采用积分图来运算，大大的加快了速度，关于积分图的介绍，可以去查阅相关的资料。

盒式滤波器和高斯滤波器的示意图如下：

上面两幅图是9×9高斯滤波器模板分别在图像垂直方向上二阶导数Lyy和Lxy对应的值，下边两幅图是使用盒式滤波器对其近似，灰色部分的像素值为0，黑色为-2，白色为1.

那么为什么盒式滤波器可以提高运算速度呢？这就涉及到积分图的使用，盒式滤波器对图像的滤波转化成计算图像上不同区域间像素的加减运算问题，这正是积分图的强项，只需要简单积分查找积分图就可以完成。

3、构造尺度空间

同SIFT算法一样，SURF算法的尺度空间由OO组SS层组成，不同的是图片的尺寸,

SIFT算法下一组图像的长宽均是上一组的一半，同一组图像的尺寸一样，组内各层所使用的尺度空间因子(高斯模糊系数σ)逐渐增大；即:同组尺寸相同,同层模糊系数相同.

而在SURF算法中，图像的尺寸是始终不变的，在滤波器金字塔中,仍然是: 同组尺寸相同,同层模糊系数相同, 即: 同组中滤波器尺寸相同, 模糊系数增大, 不同组滤波器的尺寸逐渐增大。如下图所示：

SURF中,把盒式滤波器构造了一个倒金字塔空间,而图片尺寸是始终不变的,

左图是传统方式建立一个如图所示的金字塔结构，图像的寸是变化的，并且运算会反复使用高斯函数对子层进行平滑处理，右图说明Surf算法使原始图像保持不变而只改变滤波器大小。Surf采用这种方法节省了降采样过程，其处理速度自然也就提上去了。

4. 寻找极大极小值点

将每个像素点与其所在的那幅图像邻域的8个像素，它所在的向量尺度空间上下2幅图对应位置邻域各9个点，总共26个点进行像素值比较，如果该点是最大或者最小点，就暂时列为特征点。

记住:垂直于边缘的方向, 是梯度方向,就是变化率最大的方向, 就是图像变化最明显的方向

　　其邻图如下：

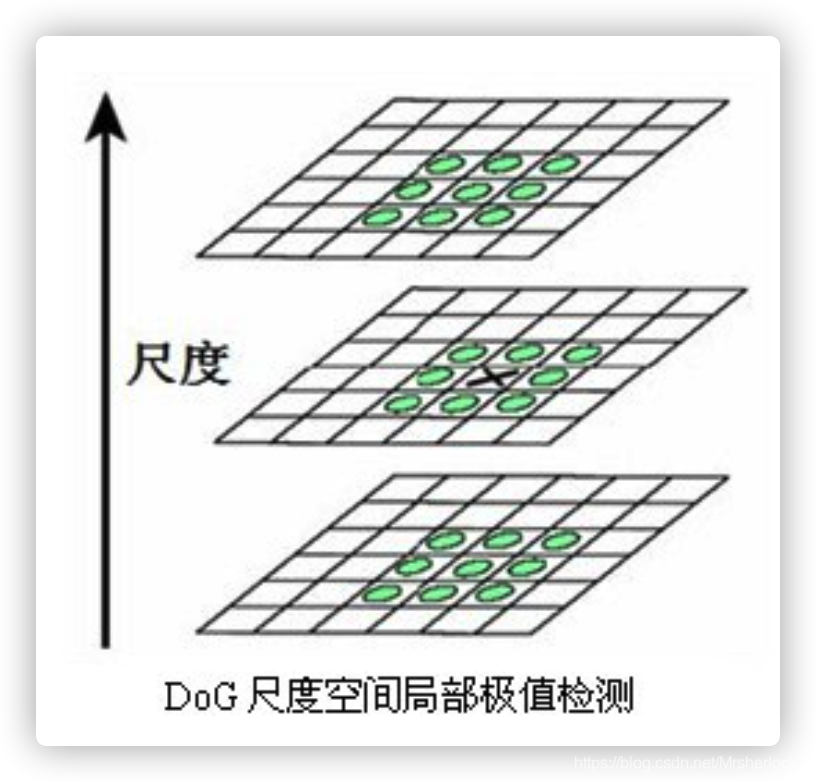
5. 精确定位极值点

亚像素级极值点：

　　由于上面找到的近似极值点落在像素点的位置上，实际上我们在像素点附近如果用空间曲面去拟合的话，很多情况下极值点都不是恰好在像素点上，而是在附近。所以sift算法提出的作者用泰勒展开找到了亚像素级的特征点。这种点更稳定，更具有代表性。

　　消除对比度低的特征点：对求出亮度比较低的那些点直接过滤点，程序中的阈值为0.03.

　　消除边界上的点：处理方法类似harrs角点，把平坦区域和直线边界上的点去掉，即对于是边界上的点但又不是直角上的点,sift算法是不把这些点作为特征点的。

6.选取特征点主方向

计算颜色直方图需要将颜色空间划分为若干小的颜色区间，即直方图的bin，通过计算颜色在每个小区间内德像素得到颜色直方图，bin越多，直方图对颜色的分辨率越强，但增加了计算机的负担。即（图所分10个竖条区域，每个竖条区域称为一个bin）

在特征点附近选取一个区域，该区域大小与图像的尺度有关，尺度越大，区域越大。并对该区域统计36个bin的方向直方图，将直方图中最大bin的那个方向作为该点的主方向，另外大于最大bin80%的方向也可以同时作为主方向。

注意:这里只是说直方图最大bin所在方向, 此时没有说y轴是梯度值还是其他值, SIFT的y轴是梯度值,SURF的y轴是haar小波特征.

这样的话，由于1个特征点有可能有多个主方向，所以一个特征点有可能有多个128维的描述子。如下图所示：

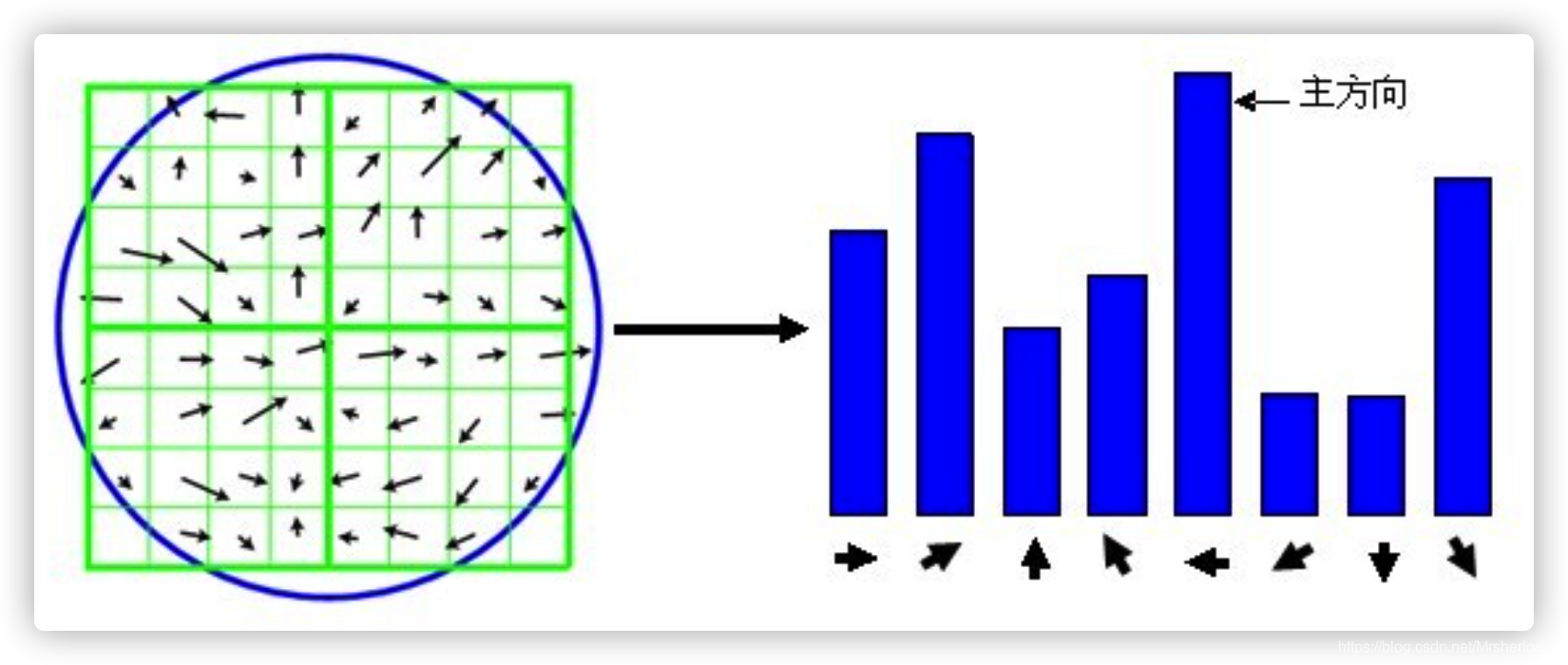
这一步与sift也大有不同。Sift选取特征点主方向是采用在特征点领域内统计其梯度直方图，取直方图bin值最大的以及超过最大bin值80%的那些方向做为特征点的主方向。

而在surf中，不统计其梯度直方图，而是统计特征点领域内的harr小波特征。

即在特征点的领域(比如说，半径为6s的圆内，s为该点所在的尺度)内，统计60度扇形内所有点的水平haar小波特征和垂直haar小波特征总和，haar小波的尺寸变长为4s，这样一个扇形得到了一个值。然后60度扇形以一定间隔进行旋转，最后将最大值那个扇形的方向作为该特征点的主方向。该过程的示意图如下：

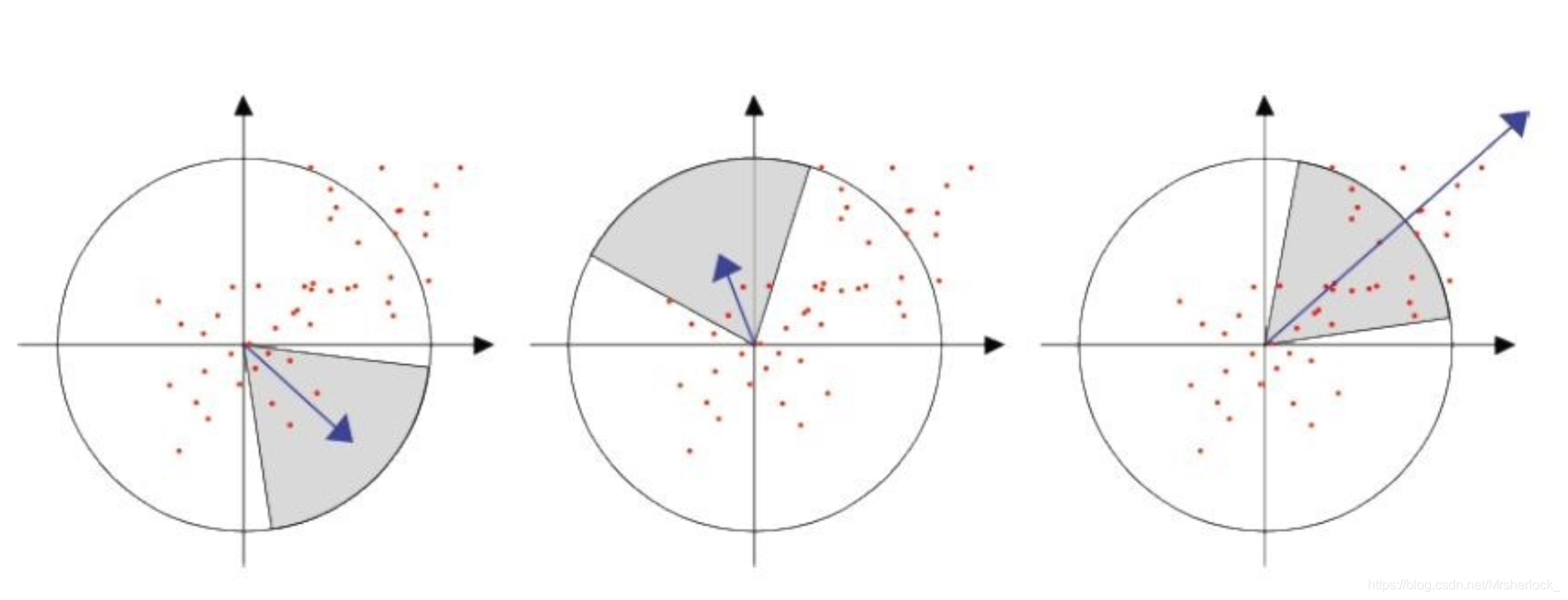
7.构造特征点描述算子

以特征点为中心，取领域内16*16大小的区域，并把这个区域分成4*4个大小为4*4的小区域，每个小区域内计算加权梯度直方图，该权值分为两部分，其一是该点的梯度大小，其二是改点离特征点的距离(二维高斯的关系)，每个小区域直方图分为8个bin，所以一个特征点的维数=4*4*8=128维。

在SIFT算法中，为了保证特征矢量的旋转不变性，先以特征点为中心，在附近邻域内将坐标轴旋转θ（特征点的主方向）角度，然后提取特征点周围4×4个区域块，统计每小块内8个梯度方向，这样一个关键点就可以产生128维的SIFT特征向量。

SURF算法中，也是提取特征点周围4×4个矩形区域块，但是所取得矩形区域方向是沿着特征点的主方向，而不是像SIFT算法一样，经过旋转θ角度。每个子区域统计25个像素点水平方向和垂直方向的Haar小波特征，这里的水平和垂直方向都是相对主方向而言的。

该Harr小波特征为水平方向值之和、垂直方向值之和、水平方向值绝对值之和以及垂直方向绝对之和4个方向。该过程示意图如下：

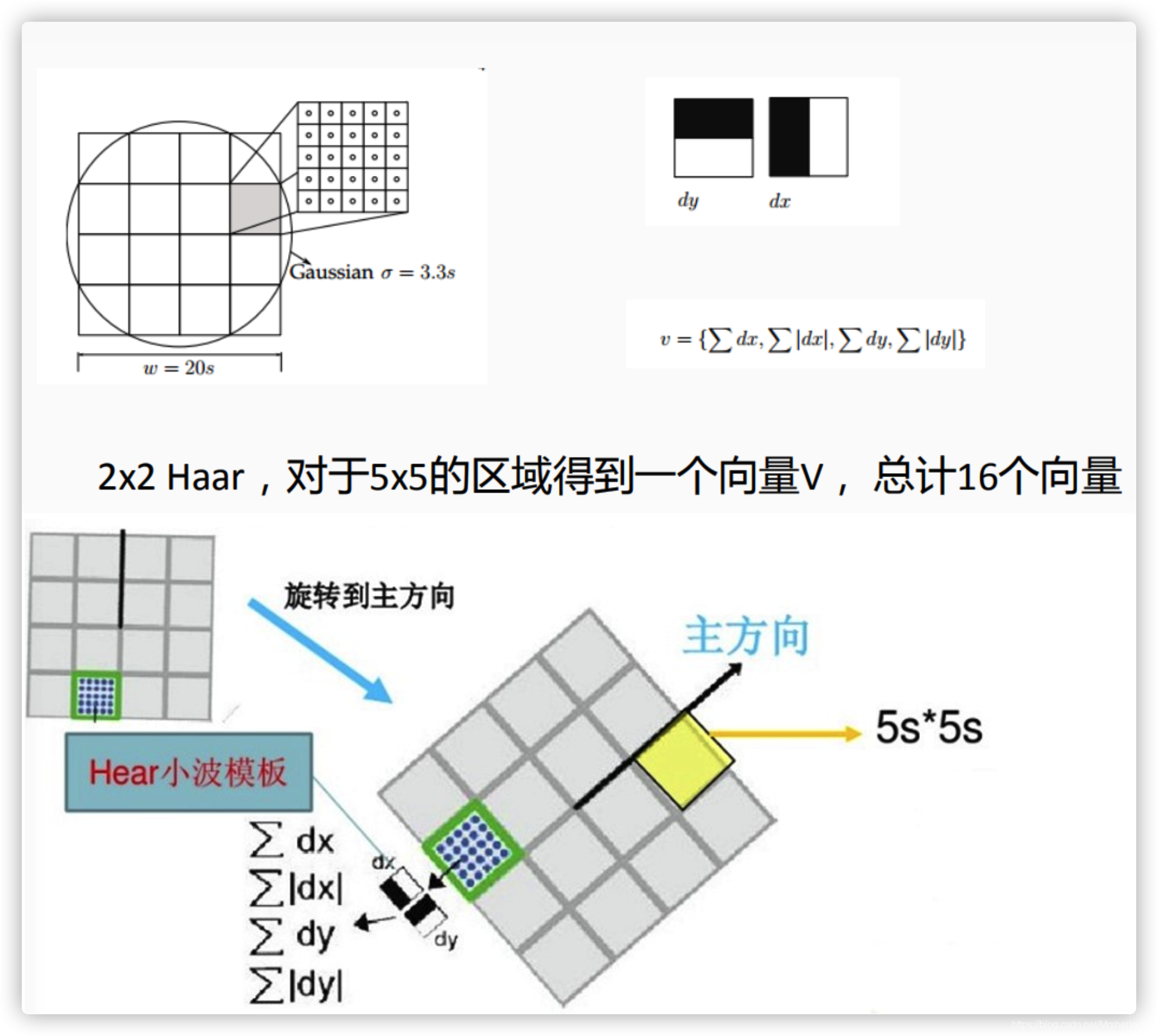
把这4个值作为每个子块区域的特征向量，所以一共有4×4×4=64维向量作为SURF特征的描述子，比SIFT特征的描述子减少了一半。

HOG特征检测

1、HOG特征：

方向梯度直方图（Histogram of Oriented Gradient, HOG）特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。

它通过计算和统计图像局部区域的梯度方向直方图来构成特征。

Hog特征结合SVM分类器已经被广泛应用于图像识别中，尤其在行人检测中获得了极大的成功。

需要提醒的是，HOG+SVM进行行人检测的方法是法国研究人员Dalal在2005的CVPR上提出的，而如今虽然有很多行人检测算法不断提出，但基本都是以HOG+SVM的思路为主。

一般情况, 在行人检测中由于每个人的内在特征存在明显的差异,因此需要一个能够全面描述人体特征的描述子进行描述,而HOG正是基于这个基本思想设计的.

HOG算子认为局部目标的表象和形状,能够被gradient或者边缘的方向密度分布很好的描述(当然gradient是梯度,而梯度往往存在于边缘处)

HOG特征提取的过程就是绘制图像的梯度分布直方图,然后利用算法,把梯度直方图归一化处理,正是这种归一化算法,将会很有效的检测出哪里是边缘,经过标准化,梯度直方图会被压缩成一个特征向量,就是HOG特征描述子,该描述子保存了大量的边缘信息,最终作为SVM分类器的输入

（1）主要思想：

在一副图像中，局部目标的表象和形状（appearance and shape）能够被梯度或边缘的方向密度分布很好地描述。（本质：梯度的统计信息，而梯度主要存在于边缘的地方）。

（2）具体的实现方法是：

首先将图像分成小的连通区域，我们把它叫细胞单元。然后采集细胞单元中各像素点的梯度的或边缘的方向直方图。最后把这些直方图组合起来就可以构成特征描述器。

（3）提高性能：

把这些局部直方图在图像的更大的范围内（我们把它叫区间或block）进行对比度归一化（contrast-normalized），所采用的方法是：先计算各直方图在这个区间（block）中的密度，然后根据这个密度对区间中的各个细胞单元做归一化。通过这个归一化后，能对光照变化和阴影获得更好的效果。

（4）优点：

与其他的特征描述方法相比，HOG有很多优点。首先，由于HOG是在图像的局部方格单元上操作，所以它对图像几何的和光学的形变都能保持很好的不变性，这两种形变只会出现在更大的空间领域上。

其次，在粗的空域抽样、精细的方向抽样以及较强的局部光学归一化等条件下，只要行人大体上能够保持直立的姿势，可以容许行人有一些细微的肢体动作，这些细微的动作可以被忽略而不影响检测效果。因此HOG特征是特别适合于做图像中的人体检测的。

2、HOG特征提取算法的实现过程：

大概过程：HOG把图像分成了很多个block, 每个block又分成了多个cell

HOG特征提取方法就是将一个image（你要检测的目标或者扫描窗口）：

1）灰度化（将图像看做一个x,y,z（灰度）的三维图像）；cvtColor();

2）采用Gamma校正法对输入图像进行颜色空间的标准化（归一化）；目的是调节图像的对比度，降低图像局部的阴影和光照变化所造成的影响，同时可以抑制噪音的干扰；

3）计算图像每个像素的梯度（包括大小和方向）；主要是为了捕获轮廓信息，同时进一步弱化光照的干扰。 Sobel算子等

4）将图像划分成小cells（例如6*6像素/cell）；

5）统计每个cell的梯度直方图（不同梯度的个数），即可形成每个cell的descriptor；

6）将每几个cell组成一个block（例如3*3个cell/block），一个block内所有cell的特征descriptor串联起来便得到该block的HOG特征descriptor。

7）将图像image内的所有block的HOG特征descriptor串联起来就可以得到该image（你要检测的目标）的HOG特征descriptor了。这个就是最终的可供分类使用的特征向量了。

每个cell是8*8个像素

nBins表示在一个胞元（cell）中统计梯度的方向数目，例如nBins=9时，在一个胞元内统计9个方向的梯度直方图，每个方向为180/9=20度。

HOG描述子维度

在确定了上述的参数后，我们就可以计算出一个HOG描述子的维度了。OpenCV中的HOG源代码是按照下面的式子计算出描述子的维度的。

进一步理解HOG描述子的产生过程:

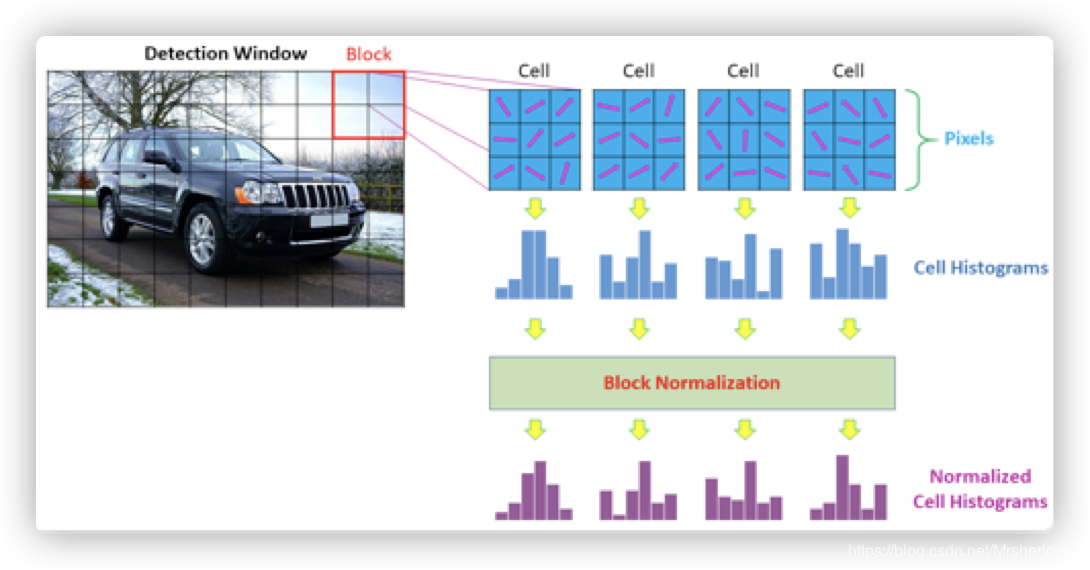
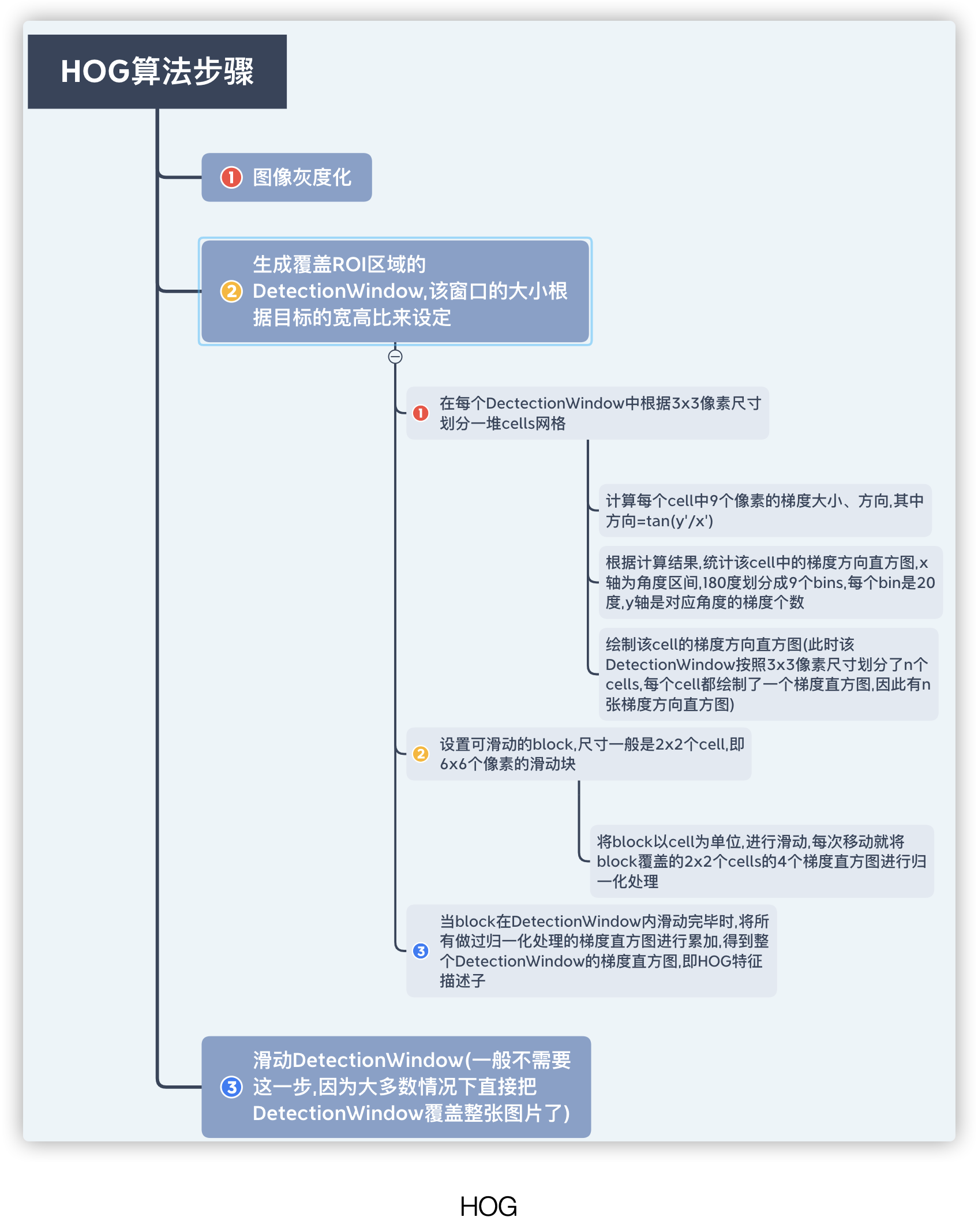
根据上图显示,一个HOG描述子的长度=block个数 ✖️ 一个block覆盖cell个数 ✖️ 每个cell的直方图中bins个数.

如果一幅图片中包含了多个DetectionWindow,那么一张图片中的HOG描述子的长度=窗口个数✖️一个HOG描述子长度

在openCV中,提供了关于HOG描述子的案例,比如下面的行人检测案例.在下面的案例中,HOGDescriptor作为HOG描述子的类,hog是类对象,该类的构造函数为默认构造函数.HOGDescriptor类存在一个svmDetector公共属性,他是用来配置HOG描述子输入给的SVM分类器的系数值的.

在上述的hog类对象中,默认构造一个64*128,的DetectionWindow,16*16的block,8*8的cell,且每个cell的HOG中含9个bins


// HOG描述子
cv2.HOGDescriptor(  win_size = (64, 128),   //前5个最常用
                    block_size = (16, 16), 
                    block_stride = (8, 8), //这个是块之间的x距离和y距离
                    cell_size = (8, 8), 
                    nbins = 9, 
                    win_sigma = DEFAULT_WIN_SIGMA, 
                    threshold_L2hys = 0.2, 
                    gamma_correction = true, 
                    nlevels = DEFAULT_NLEVELS)
// 计算描述子数值类方法
HOGDescriptor::compute(image) //输入图像
 
virtual void cv::HOGDescriptor::compute 
(
InputArray img,
std::vector< float > &descriptors,//输出HOG描述子
Size winStride = Size(),  //窗口与窗口之间的距离
Size padding = Size(),    //窗口的步长
const std::vector< Point > &locations = std::vector< Point >()d
)const

opencv案例


Mat gray;
Mat dst;
resize(src, dst, Size(64,128));
cvtColor(dst, gray, COLOR_BGR2GRAY);
HOGDescriptor detector(Size(64,128), Size(16,16), Size(8,8), Size(8,8), 9);
 
vector<float> descriptors;
vector<Point> locations;
 
detector.compute(gray, descriptors, Size(0,0),Size(0,0),locations);
cout<<“result number of HOG = “<<descriptors.size()<<endl;

DPM特征(可形变部件模型)

DPM特征是Deformable Parts Model可形变部件模型,

DPM是传统目标检测算法的天花板,是HOG特征检测算法的扩展与改进,

由于HOG往往带来高纬度的特征向量,这些特征向量作为SVM分类器的输入,往往产生很大的计算量,

HOG一般采用PCA主成分分析法降维,但DPM作为HOG算法的改进,采用了一种逼近PCA的降维方法.

首先规定前提,DPM把梯度方向根据180度和360度分成了有符号和无符号两类,其中有符号表示有正负符号,其0-360角度范围的梯度看成有方向的,分成18个bins,0-180的成为无方向的分成9个bins, 显然无路方向有无,每个bin的角度都是20度.

在对该流程的理解过程中或许有偏差,但是最终的结果是一样的,另一个理解角度是:

采用HOG的cell思想,每8✖️8个像素为一个cell,均分图片成多个cell,计算全部像素的梯度大小和方向,统计每个cell中所有像素的梯度直方图
对每个cell的4邻域的4个cell,即对角线上4个cell,如图1234(上图绿色为一个cell内部情况,黄色块为一个cell简笔画), 把该cell和4邻域的4个cell对应做归一化处理见下一步
中心cell和4邻域4个cell分别归一化处理步骤:
- 对于有符号梯度: 计算中心cell和第i个cell(i=1,2,3,4)的梯度方向直方图,在有符号的梯度方向直方图为18个bins,4个cell直方图累加得到18个bins即18个特征
- 对于无符号梯度:如图右侧,把上图橘色块即36个特征看成一个矩阵,进行行求和、列求和,共得到4+9=13个特征**
- 归一化后合计得到18+13=31个特征,即每个8✖️8像素的cell会产生一个31维的特征向量

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/AllinToyou/article/detail/337008