NLP实践系列：3、特征选择_文本分类 tf-idf 特征选择 选择排名靠前

1. TF-IDF原理与概念

TF-IDF是Term Frequency - Inverse Document Frequency的缩写，即“词频-逆文本频率”。它由两部分组成，TF和IDF。
前面的TF也就是我们前面说到的词频，我们之前做的向量化也就是做了文本中各个词的出现频率统计，并作为文本特征，这个很好理解。关键是后面的这个IDF，即“逆文本频率”如何理解。在上一节中，我们讲到几乎所有文本都会出现的"to"其词频虽然高，但是重要性却应该比词频低的"China"和“Travel”要低。我们的IDF就是来帮助我们来反应这个词的重要性的，进而修正仅仅用词频表示的词特征值。
概括来讲， IDF反应了一个词在所有文本中出现的频率，如果一个词在很多的文本中出现，那么它的IDF值应该低，比如上文中的“to”。而反过来如果一个词在比较少的文本中出现，那么它的IDF值应该高。比如一些专业的名词如“Machine Learning”。这样的词IDF值应该高。一个极端的情况，如果一个词在所有的文本中都出现，那么它的IDF值应该为0。
上面是从定性上说明的IDF的作用，那么如何对一个词的IDF进行定量分析呢？这里直接给出一个词x的IDF的基本公式如下：
IDF(x)=logNN(x)
　　　　其中，N代表语料库中文本的总数，而N(x)代表语料库中包含词x的文本总数。为什么IDF的基本公式应该是是上面这样的而不是像N/N(x)这样的形式呢？这就涉及到信息论相关的一些知识了。感兴趣的朋友建议阅读吴军博士的《数学之美》第11章。

上面的IDF公式已经可以使用了，但是在一些特殊的情况会有一些小问题，比如某一个生僻词在语料库中没有，这样我们的分母为0， IDF没有意义了。所以常用的IDF我们需要做一些平滑，使语料库中没有出现的词也可以得到一个合适的IDF值。平滑的方法有很多种，最常见的IDF平滑后的公式之一为：
IDF(x)=logN+1N(x)+1+1
　　　　有了IDF的定义，我们就可以计算某一个词的TF-IDF值了：
TF−IDF(x)=TF(x)∗IDF(x)
　　　　其中TF(x)指词x在当前文本中的词频。

2. 文本矩阵化，使用词袋模型，以TF-IDF特征值为权重。

import numpy as np
from sklearn import preprocessing
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer

#词袋模型
vec=CountVectorizer(min_df=3,ngram_range=(1,1))
content=[
    '<s[NULL]cript>alert(1)</s[NULL]cript>X</a>',
    '\'><video><source o?UTF-8?Q?n?error="alert(1)">',
    '\'><FRAMESET><FRAME RC=""+"javascript:alert(\'X\');"></FRAMESET>',
    '"></script>\'//<svg "%0Aonload=alert(1) //>',
    '"></script><img \'//"%0Aonerror=alert(1)// src>',
    'id%3Den%22%3E%3Cscript%3Ealert%28%22AKINCILAR%22%29%3C/script%3E',
    '?a%5B%5D%3D%22%3E%3Cscript%3Ealert%28document.cookie%29%3C/script%3E',
    '><iframe src="data:data:javascript:,% 3 c script % 3 e confirm(1) % 3 c/script %3 e">',
    '?mess%3D%3Cscript%3Ealert%28document.cookie%29%3C/script%3E%26back%3Dsettings1',
    'title%3D%3Cscript%3Ealert%28%22The%20Best%20XSSer%22%29%3C/script%3E',
    '<script charset>alert(1);</script charset>',
    '"><meta charset="x-mac-farsi">??script ??alert(1)//??/script ??',
    '</script><script>/*"/*\'/**/;alert(1)//</script>#',
]

trans=TfidfTransformer()
tfidf=trans.fit_transform(vec.fit_transform(content))
print(vec.get_feature_names())
print (tfidf.toarray())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

---

[u'22', u'29', u'3c', u'3cscript', u'3d', u'3e', u'3ealert', u'alert', u'script']
[[ 0.          0.          0.          0.          0.          0.          0.
   1.          0.        ]
 [ 0.          0.          0.          0.          0.          0.          0.
   1.          0.        ]
 [ 0.          0.          0.          0.          0.          0.          0.
   1.          0.        ]
 [ 0.          0.          0.          0.          0.          0.          0.
   0.75787695  0.65239752]
 [ 0.          0.          0.          0.          0.          0.          0.
   0.75787695  0.65239752]
 [ 0.60865989  0.27418507  0.27418507  0.27418507  0.          0.54837013
   0.27418507  0.          0.16767089]
 [ 0.33715382  0.30375763  0.30375763  0.30375763  0.33715382  0.60751526
   0.30375763  0.          0.18575524]
 [ 0.          0.          0.          0.          0.          0.          0.
   0.          1.        ]
 [ 0.          0.38907452  0.38907452  0.38907452  0.43185075  0.38907452
   0.38907452  0.          0.23792861]
 [ 0.39646122  0.35719043  0.35719043  0.35719043  0.39646122  0.35719043
   0.35719043  0.          0.21843071]
 [ 0.          0.          0.          0.          0.          0.          0. 
  0.50226141  0.86471583]
 [ 0.          0.          0.          0.          0.          0.          0. 
  0.50226141  0.86471583]
 [ 0.          0.          0.          0.          0.          0.          0. 
 0.36109936  0.93252735]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

词袋模型中词汇的tf-idf值，值越高说明该词区分每条语句的效果越好。

3. 互信息的原理。

• 互信息定义：
  两个离散随机变量 X 和 Y 的互信息可以定义为：
  
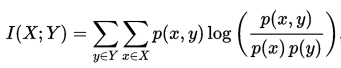
  　其中 p(x,y) 是 X 和 Y 的联合概率分布函数，而p(x)和p(y)分别是 X 和 Y 的边缘概率分布函数。

在连续随机变量的情形下，求和被替换成了二重定积分：
　　
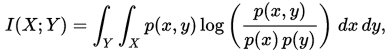
　　其中 p(x,y) 当前是 X 和 Y 的联合概率密度函数，而p(x)和p(y)分别是 X 和 Y 的边缘概率密度函数。

互信息量I(xi;yj)在联合概率空间P(XY)中的统计平均值。 平均互信息I(X;Y)克服了互信息量I(xi;yj)的随机性,成为一个确定的量。如果对数以 2 为基底，互信息的单位是bit。

直观上，互信息度量 X 和 Y 共享的信息：它度量知道这两个变量其中一个，对另一个不确定度减少的程度。例如，如果 X 和 Y 相互独立，则知道 X 不对 Y 提供任何信息，反之亦然，所以它们的互信息为零。在另一个极端，如果 X 是 Y 的一个确定性函数，且 Y 也是 X 的一个确定性函数，那么传递的所有信息被 X 和 Y 共享：知道 X 决定 Y 的值，反之亦然。因此，在此情形互信息与 Y（或 X）单独包含的不确定度相同，称作 Y（或 X）的熵。而且，这个互信息与 X 的熵和 Y 的熵相同。（这种情形的一个非常特殊的情况是当 X 和 Y 为相同随机变量时。）

互信息是 X 和 Y 联合分布相对于假定 X 和 Y 独立情况下的联合分布之间的内在依赖性。于是互信息以下面方式度量依赖性：I(X; Y) = 0 当且仅当 X 和 Y 为独立随机变量。从一个方向很容易看出：当 X 和 Y 独立时，p(x,y) = p(x) p(y)，因此：
　
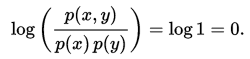
　此外，互信息是非负的，而且是对称的（即 I(X;Y) = I(Y;X)）。

4. 利用互信息进行特征筛选。

参考链接：https://blog.csdn.net/BigData_Mining/article/details/81279612
https://www.jianshu.com/p/0d7b5c226f39
https://www.cnblogs.com/pinard/p/6693230.html