AllinToyou

这个屌丝很懒，什么也没留下！

热门标签

【原版】流模型 Flow 超详解，基于 Flow 的生成式模型，从思路到基础到公式推导到模型理解与应用（Flow-based Generative Model）

作者：AllinToyou | 2024-04-07 17:32:18

踩

流模型

参考文献：

[1] Dinh L, Krueger D, Bengio Y. Nice: Non-linear independent components estimation[J]. arXiv preprint arXiv:1410.8516, 2014.

[2] Dinh L, Sohl-Dickstein J, Bengio S. Density estimation using real nvp[J]. arXiv preprint arXiv:1605.08803, 2016.

[3] Kingma D P, Dhariwal P. Glow: Generative flow with invertible 1x1 convolutions[J]. Advances in neural information processing systems, 2018, 31.

[4] 台大教授李宏毅 Flow-based Generative Model哔哩哔哩bilibili

[5] 细水长flow之NICE：流模型的基本概念与实现 - 科学空间|Scientific Spaces

[6] 细水长flow之RealNVP与Glow：流模型的传承与升华 - 科学空间|Scientific Spaces

[7] 随机变量的变量替换定理(Change of Variable Theorem) - 郑之杰的个人网站 (0809zheng.github.io)

[8] Glow: Better reversible generative models (openai.com)

[9] Oord A, Li Y, Babuschkin I, et al. Parallel wavenet: Fast high-fidelity speech synthesis[C]//International conference on machine learning. PMLR, 2018: 3918-3926.

[10] Prenger R, Valle R, Catanzaro B. Waveglow: A flow-based generative network for speech synthesis[C]//ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2019: 3617-3621.

初识 Flow

数学基础与核心公式推导

雅可比矩阵（Jacobian Matrix）

行列式（Determinant）

变量变换定理（Change of Variables Theorem）

补充：1×1 卷积（1×1 Convolution）

由于公式涉及太多，CSDN 博客有bug，有时候无法清晰显示公式，因此特地提供使用 md 编辑器发布的相同文章博客：【清晰公式版】流模型 Flow 超详解，基于 Flow 的生成式模型，从思路到基础到公式推导到模型理解与应用（Flow-based Generative Model）-CSDN博客其中内容相同，但公式一定会加载清晰，欢迎大家查看。

初识 Flow

非常推荐大家查看我之前介绍 VAE 的一篇博客：变分自编码器 VAE 超详解，从简单公式推导到模型结构到模型理解-CSDN博客，这其中有一些知识基础引入。此外，我也在对 Vocoder 的讲解中介绍了 Flow 模型的应用： WaveGlow，在看完这篇博客后也欢迎大家前往查看：Vocoder，声码器详解——语音信号处理学习（十）_音乐的vocoder模型-CSDN博客，其中也包括对自回归模型 WaveNet 的讲解。

相信看到标题，大家应该都可以明白，Flow 本质上也是一个生成式模型（Generative Model），和 GAN、VAE、自回归模型的性质是一样的。我们简单回顾一下：
- 自回归模型（Auto-regressive Model）诸如 WaveNet 生成出来的声音质量确实很高，但是由于它是按照某种顺序一点一点生成的，因此生成速度非常的慢，甚至需要用90分钟来生成1秒的声音，这也就导致其不太能投入实际使用。
- VAE 也很不错，然而我们讲过，VAE 优化的是一个变分下界（ELBO），是做了一个迂回，而并不是去最大化我们真正的目标函数 p(x)，因此最终的效果也不是特别好。
- GAN 呢？在图像生成领域它的质量还是非常好的，然而，它非常难以训练，因为它需要同时训练生成器和判别器，而这两者的训练目标是不一样的，很容易就训练崩溃了。
而 Flow 相较于 VAE 来讲，它就是简单直接的。我不跟你兜圈子，我直接最大化概率分布 p(X)！
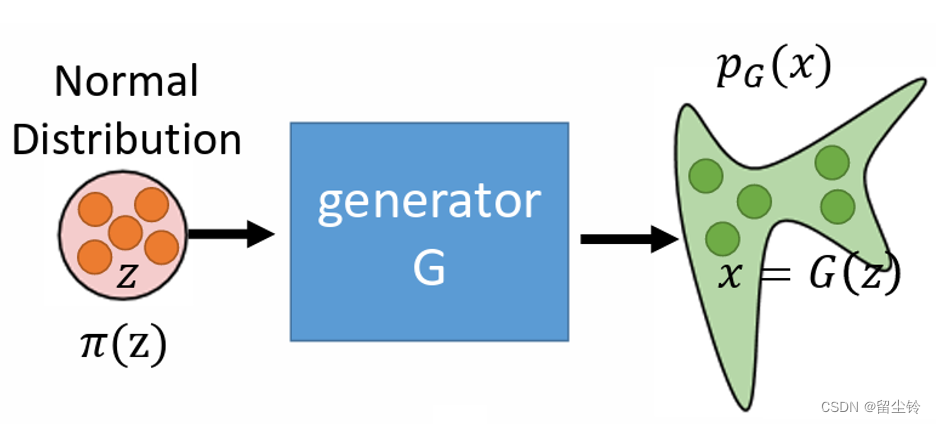
不过，先别急着去学习 Flow。在讲 Flow 之前，我们首先重新来回顾一下生成式模型。生成式模型，其最重要的就是 Generator，生成器。我们一般是从一个正态分布（Normal Distribution）中采样（sample）出来一个 z，然后再将 z 送入生成器中，之后就能得到输出 x。我们将生成器记为 G，整个过程用公式表示为：

$x = G(z)$

而这个过程本质上，就是从正态分布映射到一个新的概率分布中，新的概率分布我们希望就是生成目标所在的概率分布。我们将这个正态分布记为 π，将生成器所映射的概率分布称为 p_G，示意图如下所示：
那么怎么样才算是一个好的生成器呢？我们希望，由生成器定义出的概率分布 p_G 要尽可能接近真实数据的概率分布 p_data。这里的 p_data 就是所有的生成目标所形成的概率分布，比如我们要生成的是人脸图像，p_data 就是这世间所有可能的人脸图像所构成的概率分布。
那怎样才能让 p_G 尽可能接近 p_data 呢？一种常见的办法就是最大似然估计（ML，Maximum Likelihood），也就是最大化产生样本的概率 p_G(x)。即，从人脸照片中拿出 m 张图片（样本），这 m 张图片由 G 产生出来的概率越大越好，用公式表达为：

$G^* = \arg \max_G \sum_{i=1}^{m}\log P_G(x^i)$
- 其中，{x^i} 来自于 p_data。
这就是我们的目标函数（Objective Function）。当然，还有另外一种理解，就是最小化 p_data 与 p_G 的差异（KL 散度），也就是实际意义上的让 p_data 与 p_G 越相近越好，用公式写就是：

$\begin{aligned} G^* &= \arg \max_G \sum_{i=1}^{m}\log P_G(x^i) \\ & \approx \arg \min KL(P_{data}||P_G) \end{aligned}$
而 Flow 模型厉害在什么地方呢？在实际训练中，G 身为一个神经网络，它的 p_G 是很复杂的，我们往往无法直接最大化 p_G，也就是直接最大化我们的目标函数，比如 VAE 改成最大化目标函数的一个下界等等。但是！Flow 却有一种办法，可以做到直接最大化我们的目标函数！下面我们就来介绍一下 Flow 究竟是怎么做到的。

数学基础与核心公式推导

在讲 Flow 的原理之前，我们需要先简单了解一些数学基础。如果不想深入了解可以就看下面的内容，想要深入了解也请根据关键词自行搜索学习。

实际上，Flow 之所以没有 GAN 那么出名，很可能就是因为其涉及到的数学原理太多，而没有 GAN 那样可以用很形象的概念去解释。接下来，我们将会简单介绍 Flow 涉及到的关键数学基础：雅可比矩阵（Jacobian Matrix）、行列式（Determinant）、变量变换定理（Change of Variables Theorem）

雅可比矩阵（Jacobian Matrix）

假设我们有两个二维向量 z、x，有一个函数 f。f 的输入为 z，输出为 x。当然，你可以将 f 想象成生成器 G，z 和 x 就是生成器的输入和输出。而 f 的雅可比矩阵就是将 z 和 x 的内容物两两偏微分，最后形成出来的矩阵就是 f 的雅可比矩阵，其示意公式图如下：
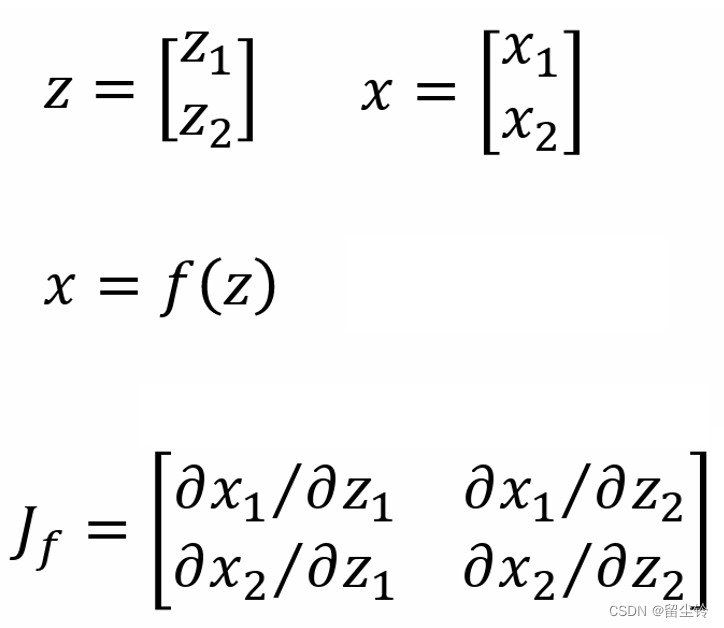
在雅可比矩阵中，不同的行有着不同的输出作为分子，不同的列有不同的输入作为分母。我们举一个简单的例子。z 和 x 的式子如下：
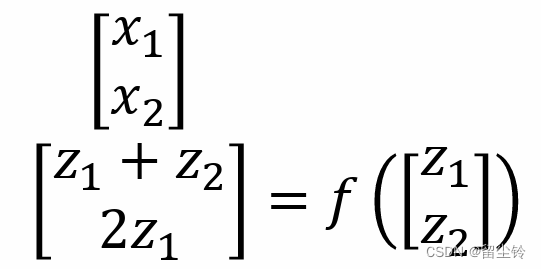
则，其雅可比矩阵就为，第一行分别是 z1 和 z2 对 z1+z2 的偏微分，第二行分别是 z1 和 z2 对 2z1 的偏微分，结果如下：
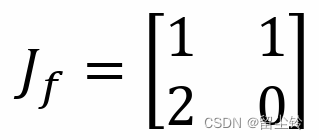
而如果我们现在提供 f^-1，也就是 f 的逆函数，即输入为 x，输出为 z，那么 f^-1 的雅可比矩阵就为：
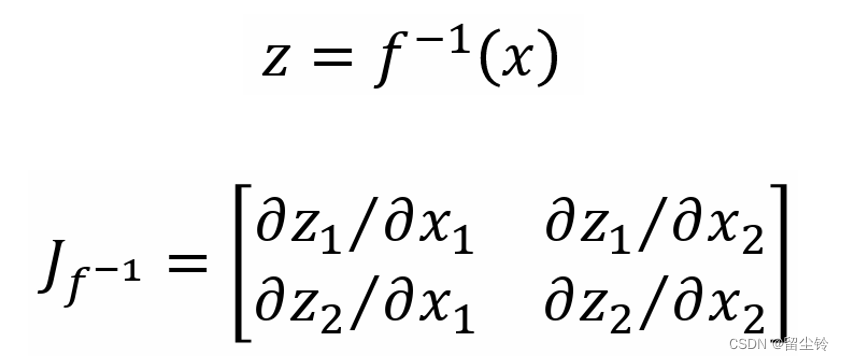
而将 f 的雅可比矩阵和 f 逆的雅可比矩阵放在一起比较，我们不难发现，它们相乘的结果就是单位矩阵 I：
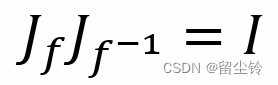
也就是说，J_f 和 J_f-1 互为逆矩阵。就拿我们刚刚举的例子来说：
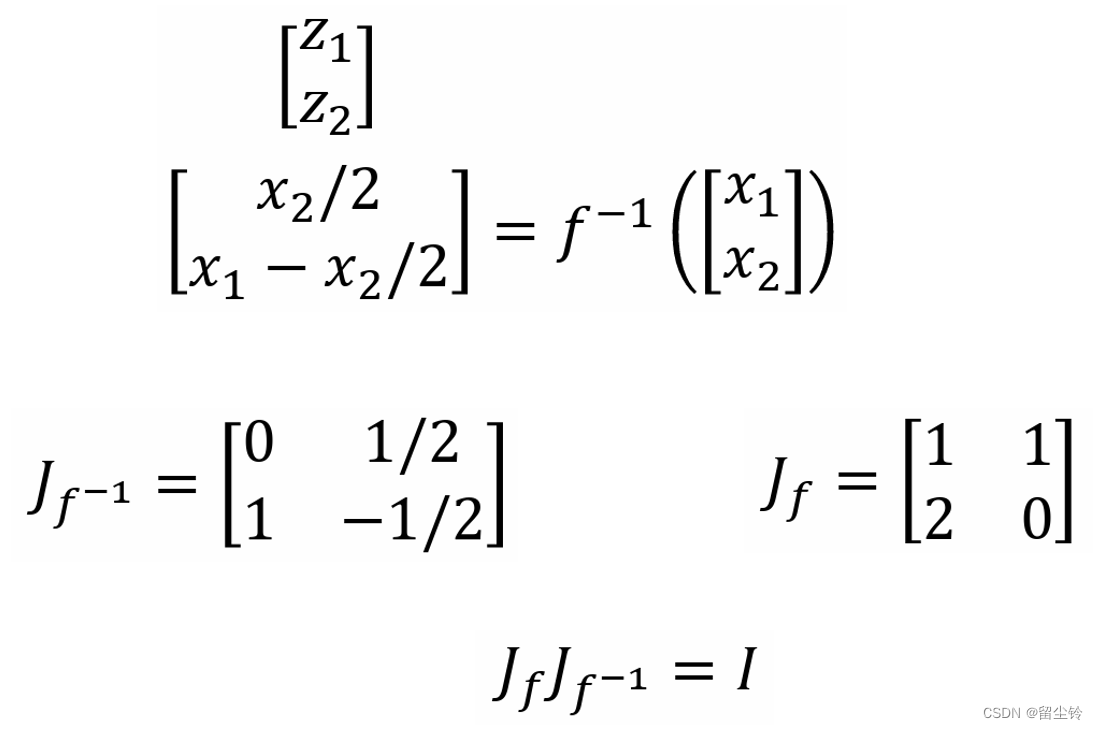
所以我们可以得到一个结论：如果两个函数互逆，则它们的雅可比矩阵也互逆。这个结论在后面也会用到。

行列式（Determinant）

行列式相信大家在高中阶段就已经学习过了。我们在这里规范一下写法。在公式中，我们使用 det 来表示某一个矩阵的行列式。如 2*2 矩阵、3*3的行列式为：
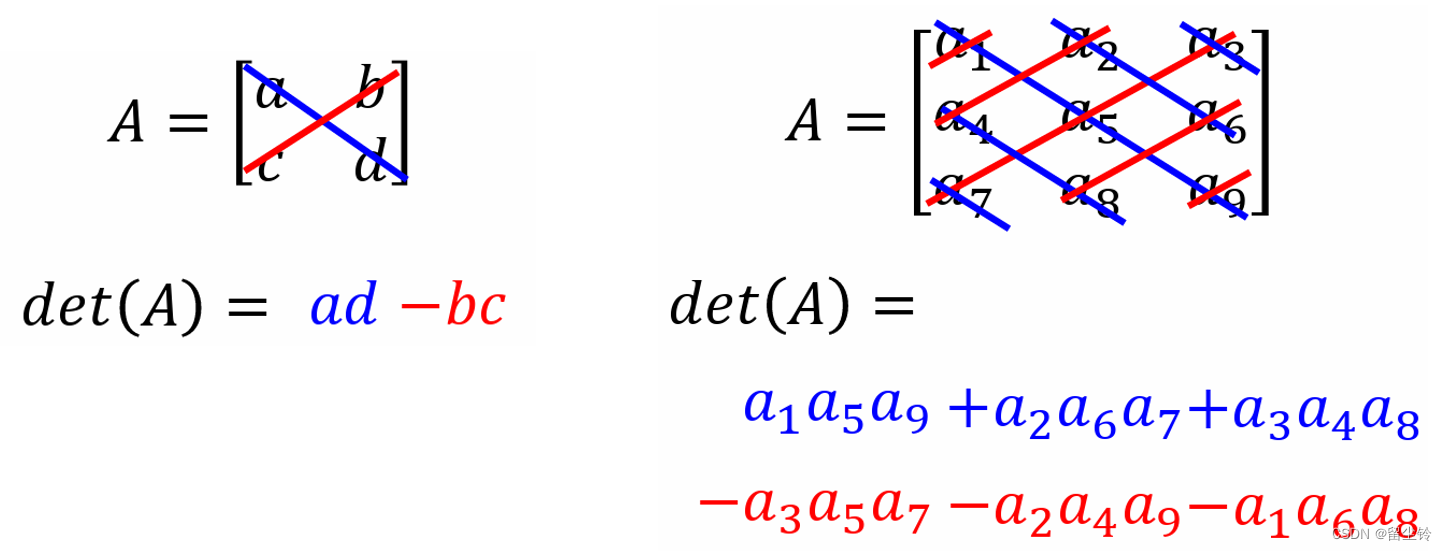
而关于行列式，我们也有一个结论，即：互逆的矩阵的行列式的值互为倒数，写作：

$\det(A) = \frac{1}{\det(A^{-1})}$
结合雅可比矩阵，我们不难推出下面的结论：

$\det(J_f) = \frac{1}{\det(J_{f^{-1}})}$

记住这个结论！后面要考！！！
行列式我们都知道，那行列式究竟有什么意义呢？实际上，行列式的值我们可以看作是高维空间中的 “体积” 的概念。我们拿 2*2 的矩阵来举例，将矩阵的每一行视作是一个向量，则我们可以在平面坐标系中绘制出两个向量，而行列式的值的绝对值，就是这两个向量所构成的图形的面积。
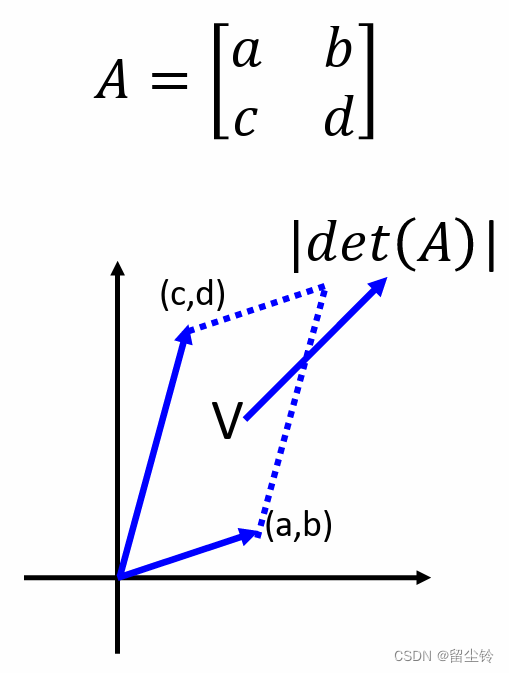
如此一来，3*3 的矩阵也是同理，将每一行表示的向量在三维坐标系中绘制出来，则绘制出的三个向量所构成的六面体体积就是矩阵的行列式取绝对值。

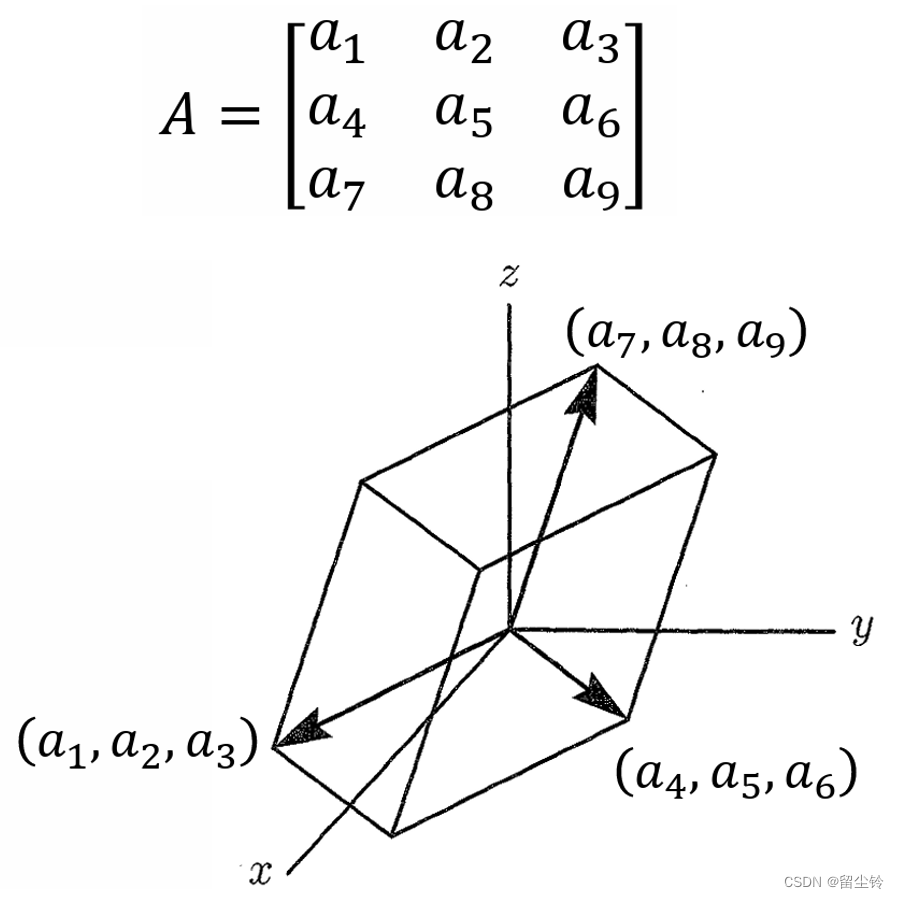
变量变换定理（Change of Variables Theorem）

讲完了行列式的意义，我们就可以来了解变量变换定理了。假设我们有两个概率分布，分别为 π of z 和 p of x，有一个函数 f，输入 z，输出为 x。你当然可以将 π 理解为正态分布，将 p 理解为目标的概率分布。因此也就是说，在知道函数 f 的情况下，如果我们能知道 π of z 和 p of x 的对应关系，那我们就可以做一个生成器，因为生成器就是概率分布之间的映射。
我们在 π 上有一个 z’，在 p 上有一个 x’，那二者的概率密度有什么关系呢？这个关系是可以写出来的吗？
关系是可以写出来的！我们先举一个简单的例子。假如 π 就是一个很简单的均匀分布（Uniform Distribution），其分布范围在 0-1 之间，由于概率密度函数的积分需要等于1，即下图中那个矩形的面积需要为1，那么 π 的高度我们就知道应该也为 1。
那么现在，假设 x 跟 z 的关系为：

$\begin{aligned} x &= f(z) \\ &= 2z+1 \end{aligned}$
那么原本在 0-1 之间的分布就被转换到 1-3 之间的分布了。我们尝试画出 x 的概率密度函数，理所应当的，这次的矩形高度应该是 0.5：
那么在这种情况下，π(z) 和 p(x) 又有什么关系呢？相信不难看出，我们随便取 π 中的一个 z’，映射到 p 上为 x’，则二者的关系就为：p(x') = 1/2 π(z')：
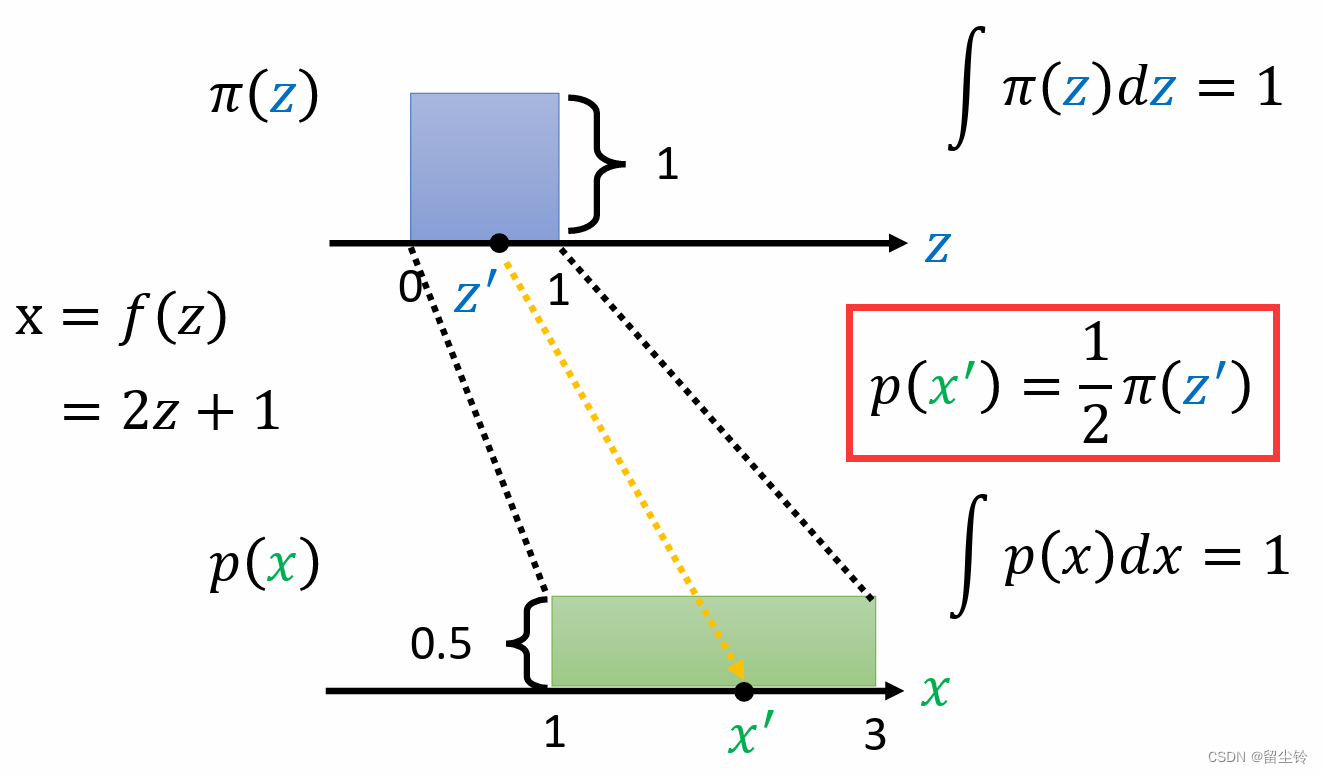
那我们再来考虑更加一般的情况。我们画出两个概率密度函数，和 z' 与 x' 的映射
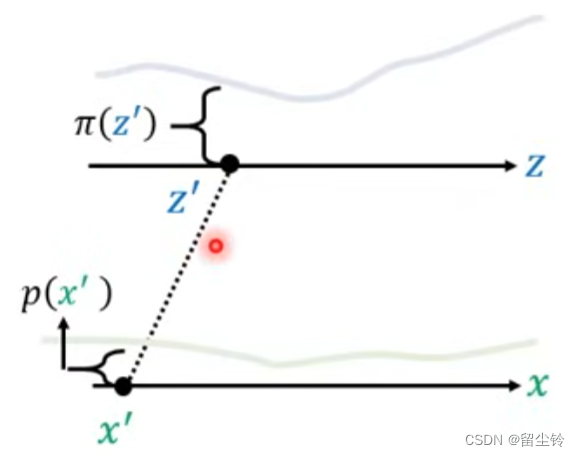
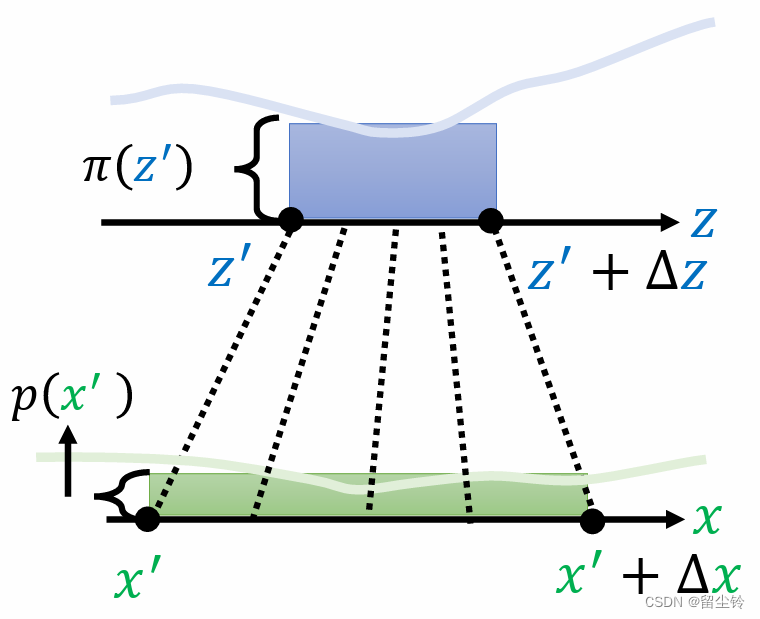
我们并不知道 π 和 p 在通常情况下的概率密度函数，我们只知道 z 和 x 的对应函数 f，那么我们能将二者的概率密度函数的关系写出来吗？我们给予 z' 一个小小的变动，记为 Δz，映射到 x 上就变成了 Δx，即 z' 到 z'+Δz，x' 到 x'+Δx：
假设这个 Δ 是非常小的一个值，那么从 z' 到 z'+Δz 之间的概率密度函数我们就可以视为均匀分布，同样，x' 到 x'+Δx 之间也可以视为均匀分布。
由于 z 和 x 之间有严格单调的对应关系 f，因此从区域 Δz 也就是蓝色方块，到区域 Δx 也就是绿色方块，二者的映射是一一对应的，也就是二者的概率应该相同，即蓝色方块和绿色方块的面积是相同的（如不相同则会不满足归一化），因此我们可以得到这样的式子，并对齐稍加变换：

$p(x')\Delta x = \pi(z')\Delta z \\ p(x') = \pi(z')\frac{\Delta z}{\Delta x} \\$
而这个 Δ 在非常小的情况下，我们也可以写作是微分 d，不过微分可正可负，因此我们还需要额外加上绝对值符号，那么上面的式子我们就可以写成：
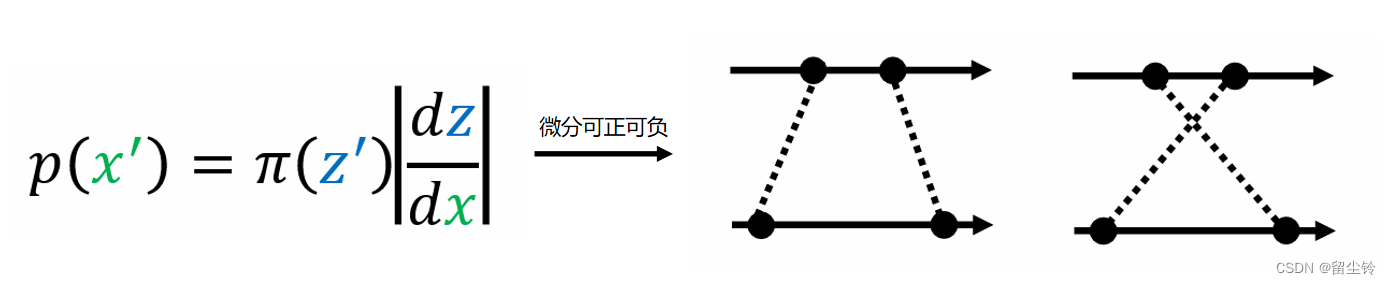
而 x 对 z 的微分，在我们知道 z 与 x 的对应关系 f 的情况下是可以求的。
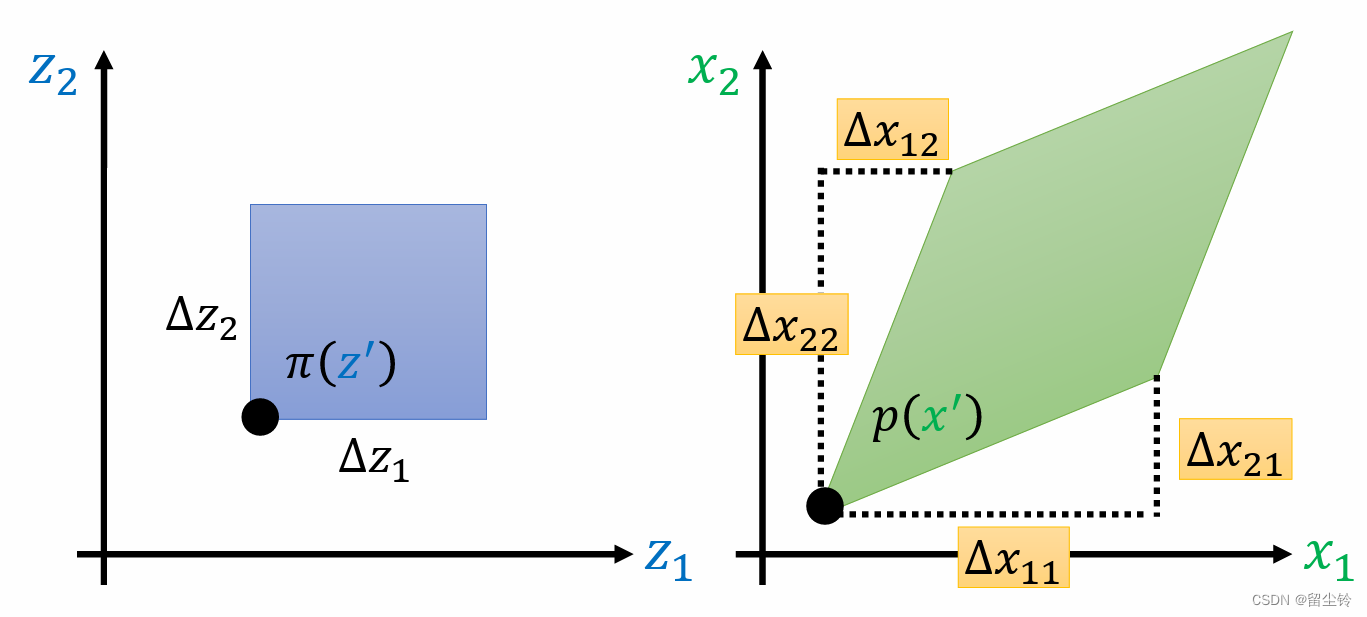
在一维的情况下是如此，那么在二维的呢？我们简单写两个二维的概率密度函数，同样对于 z'：[z1, z2]，在两个维度上我们都给予小小的变动 Δ，那么 x' 也会跟着变动，示意图如下：
其中，z' 在变成 [z1+Δz1, z2] 时，x' 变成了 [x1+Δx11, x2+Δx21]，z' 变成 [z1, z2+Δz2] 时同理。同样，在 Δ 非常小的情况下时，蓝色矩形乘以其高（即垂直于屏幕的向量，也即 π(z')）的体积也需要等于绿色四边形乘以其高（p(x')）的体积，也就是二者的概率相同。
蓝色矩形的面积好算，而那个绿色四边形的面积我们应该怎么求呢？这就需要用到我们之前介绍的行列式的几何意义。我们只要计算其两边的向量组成的行列式就可以算出四边形的面积，用公式表示如下：

$p(x')\left\vert\det \begin{bmatrix} \Delta x_{11} & \Delta x_{21} \\ \Delta x_{12} & \Delta x_{22} \\ \end{bmatrix} \right\vert = \pi(z')\Delta z_1 \Delta z_2$
我们整理一下上面的式子：

$p(x')\left\vert\det \begin{bmatrix} \Delta x_{11} & \Delta x_{21} \\ \Delta x_{12} & \Delta x_{22} \\ \end{bmatrix} \right\vert = \pi(z')\Delta z_1 \Delta z_2 \\ p(x')\left\vert\frac{1}{\Delta z_1 \Delta z_2}\det \begin{bmatrix} \Delta x_{11} & \Delta x_{21} \\ \Delta x_{12} & \Delta x_{22} \\ \end{bmatrix} \right\vert = \pi(z') \\ p(x')\left\vert\det \begin{bmatrix} \Delta x_{11}/\Delta z_1 & \Delta x_{21}/\Delta z_1 \\ \Delta x_{12}/\Delta z_2 & \Delta x_{22}/\Delta z_2 \\ \end{bmatrix} \right\vert = \pi(z') \\$
同理，Δ 很小，我们把它写成偏微分：

$p(x')\left\vert\det \begin{bmatrix} \partial x_{1}/\partial z_1 & \partial x_{2}/\partial z_1 \\ \partial x_{1}/\partial z_2 & \partial x_{2}/\partial z_2 \\ \end{bmatrix} \right\vert = \pi(z') \\$
对矩阵进行一次转置（Transpose），其行列式的值不变，因此：

$p(x')\left\vert\det \begin{bmatrix} \partial x_{1}/\partial z_1 & \partial x_{1}/\partial z_2 \\ \partial x_{2}/\partial z_1 & \partial x_{2}/\partial z_2 \\ \end{bmatrix} \right\vert = \pi(z') \\$
咦，中间的矩阵不就是我们之前所说的雅可比矩阵吗？是的，当我们知道 x=f(z) 的对应关系后，这个式子就可以写成：

$p(x')\left\vert\det (J_f) \right\vert = \pi(z') \\$
由此，我们就知道了π of z 和 p of x 之间的关系。基于雅可比矩阵的性质，我们稍稍做一个变换：

$p(x')\left\vert\det (J_f) \right\vert = \pi(z') \\ p(x') = \pi(z') \left\vert\frac{1}{\det(J_f)} \right\vert\\ p(x') = \pi(z') \left\vert\det(J_{f^{-1}}) \right\vert\\$
就此，我们就得到了 Flow 的核心公式：

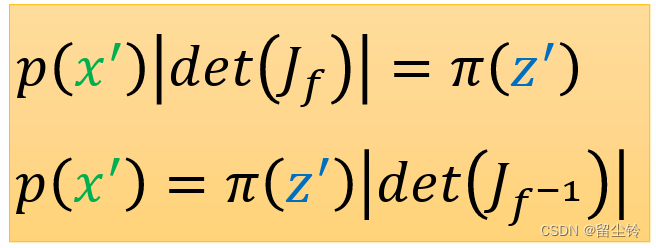
Flow 模型介绍

目标函数变换

既然得到了 π of z 和 p of x 之间的关系，我们再回到刚刚的目标函数上，因此我们就可以对目标函数进行变换：
- 由：
  
  $x = G(z) \\ G^* = \arg \max_G \sum_{i=1}^{m}\log p_G(x^i) \\$
- 以及之前推导出的核心公式，可得：
  
  $p_G(x^i) = \pi(z^i)\left\vert \det(J_{G^{-1}}) \right\vert \\ z^i = G^{-1}(x^i)$
- 进行变量替换再取 log，得：
  
  $\log p_G(x^i) = \log \pi(G^{-1}(x^i))+ \log\left\vert \det(J_{G^{-1}})\right\vert$
由此便得到了我们最终需要最大化的式子，也就是目标函数。不过，要想优化这样的目标函数是有一定的前提的，需要对 G 进行一些限制，使其能满足以下条件：
- 可以计算 det(J_G)：我们知道了生成器 G，理论上知道了 z 怎么变成 x 就很容易计算其雅可比矩阵的行列式。然而，在现实场景中，G 的输入和输出一般维度都非常高，例如 z 和 x 都是1000维向量，那么 J_G 将是一个 1000*1000 的矩阵，计算它的行列式值是非常耗费时间的。
- 知道 G^-1：式子中，也有 G^-1 的存在，我们也需要好好设计 G，让其可逆、逆可以计算、方便计算。因此为了让 G 可逆，在 Flow 模型中，输入和输出的维度一般都是一样的。
有了上述的限制，G 就不再是随便一个网络都能胜任的了，这么多限制也使得 G 的能力一定是很有限的。那我们应该怎么办？

细水长Flow

一个 G 的能力是有限的，那两个 G 呢？三个 G 呢？千千万万个 G 呢？“水流细” 没关系，只要细水长流，日积月累就能至千里。
根据上面的示意图，带入核心公式后，对于第一个G1，我们可以得到：

$p_1(x^i) = \pi(z^i)(\left\vert \det(J_{G_1^{-1}}\right\vert)$
继续往后推：

$\begin{aligned} p_2(x^i) &= p_1(x^i)(\left\vert \det(J_{G_2^{-1}}\right\vert) \\ &= \pi(z^i)(\left\vert \det(J_{G_1^{-1}}\right\vert)(\left\vert \det(J_{G_2^{-1}}\right\vert) \end{aligned}$
一直推导到第 K 个 G，有：

$p_K(x^i) = \pi(z^i)(\left\vert \det(J_{G_1^{-1}}\right\vert)\cdots(\left\vert \det(J_{G_K^{-1}}\right\vert)$
取一下 log，得：

$\log p_K(x^i) = \log \pi(z^i) + \sum_{h=1}^{K}\log\left\vert \det(J_{G_h^{-1}})\right\vert$
上面的式子就是我们未来的目标函数。而对于 z^i，我们有：

$z^i = G_1^{-1}(G_2^{-1}(\cdots G_K^{-1}(xi)))$
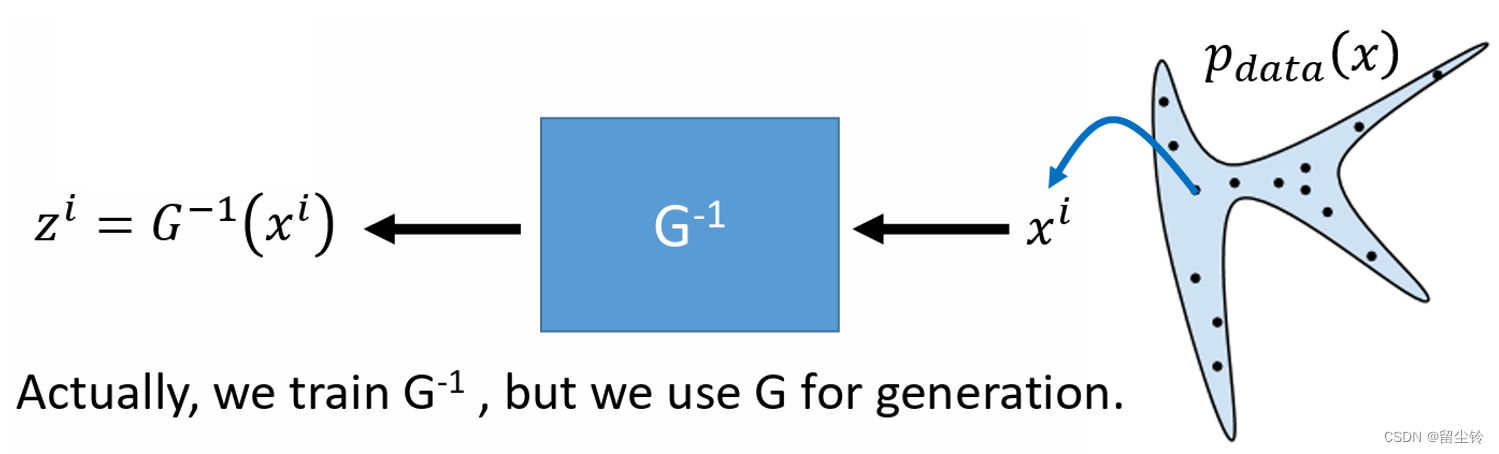
那么接下来，我们就需要最大化取了 log 的目标函数了。实际上我们是怎么去训练的呢？我们发现，其实目标函数中只出现了一系列 G^-1，也就是 G 的逆，而并没有出现 G 的本体。因此我们实际上在训练时训练的是 G^-1，即从样本到噪声，而在使用（测试）的时候才会用 G。
我们先用一个 G 的情况来举例，当只有 1 个 G 的时候，我们的目标函数就是：

$\log p_G(x^i) = \log \pi(G^{-1}(x^i))+ \log\left\vert \det(J_{G^{-1}})\right\vert$
要想将这个目标函数最大化，我们来看这个目标函数的构成：
- 首先是 log π 这一部分。我们知道，π 实际上是一个标准正态分布，要想让这一部分变大，或者说达到最大值，那么只需要 G^-1(x^i) 的输出的 z 全为零向量就行。然而，这肯定是不行的，无论输入什么样本，最后输出都是零向量，那这还得了？
- 好在我们还有第二项，我们不难发现，如果 G^-1 的输入怎么变，最终输出的都是零向量，那就代表输出对输入的各项梯度全为0，那也就是说 G^-1 的雅可比矩阵就是零矩阵（Zero Matrix），那它的行列式也就变成 0 了。把 0 带入第二项，你就会得到一个负无穷，这样整个目标函数就无法最大化。
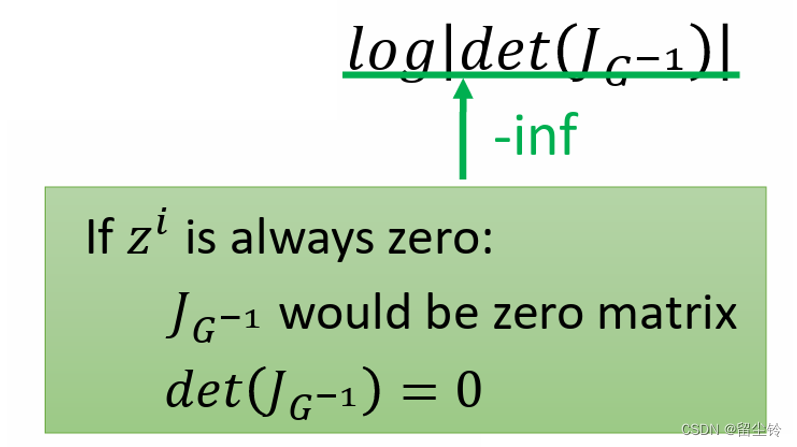
因此，要想最大化目标函数，我们就必须同时考虑这两项。一方面，第一项想尽可能将所有的 z 往原点集中，而另一方面，第二项又会对其做出限制，防止它将所有的 z 都变成零向量。

耦合层（Coupling Layer）

虽然对生成器 G 有着诸多限制，但是我们可以通过堆叠的方式增强生成器的能力。那单个 G 在这么多限制的情况下应该如何设计呢？对于应用 Flow 模型比较经典的 NICE 和 Real NVP，它们都采用了耦合层（Coupling Layer）来设计生成器。
耦合层的概念很简单。我们假设 z 和 x 都是 D 维的向量，我们将 z 拆成两组，前 d 维为一组，剩下的为另一组。生成 x 的处理方法如下：
- 前 d 维直接复制过去变成 x 的前 d 维。
- 与此同时，我们准备两个变换函数 F 和 H，这两个函数形式没有限制，可以设计得很复杂，结果需要是 D-(d+1) 维的
- 将前 d 维分别通过两个函数，得到两个结果（β 和 γ），d+1~D 维则和其中一个结果点乘，乘积再和另一个结果相加，得到 x 的 d+1~D 维，公式如下：
  
  $x_{i>d} = \beta_i z_i + \gamma_i$
- 最后，将两个部分组合，成为最终结果 x。
这样设计生成器 G，那我们怎么去得到 G 的逆呢？有了 x，我们怎么去求出 z 呢？很简单！首先，z 的前 d 维就是 x 的前 d 维，直接复制过去就行了。有了 z 的前 d 维，我们就可以通过 F 和 H 计算 β 和 γ，从而就能反推公式算出 z 的 d+1~D 维，公式如下：

$z_{i\le d} = x_i \\ z_{i>d} = \frac{x_i-\gamma_i}{\beta_i}$
从而，通过耦合层的设计，我们可以轻松得到 G 的逆。除此以外，我们还需要能计算 G 的雅可比矩阵行列式的值，那么耦合层的设计能满足这条限制吗？
我们先简单回顾一下雅可比矩阵的写法。以二维来举例，写法示意图如下：

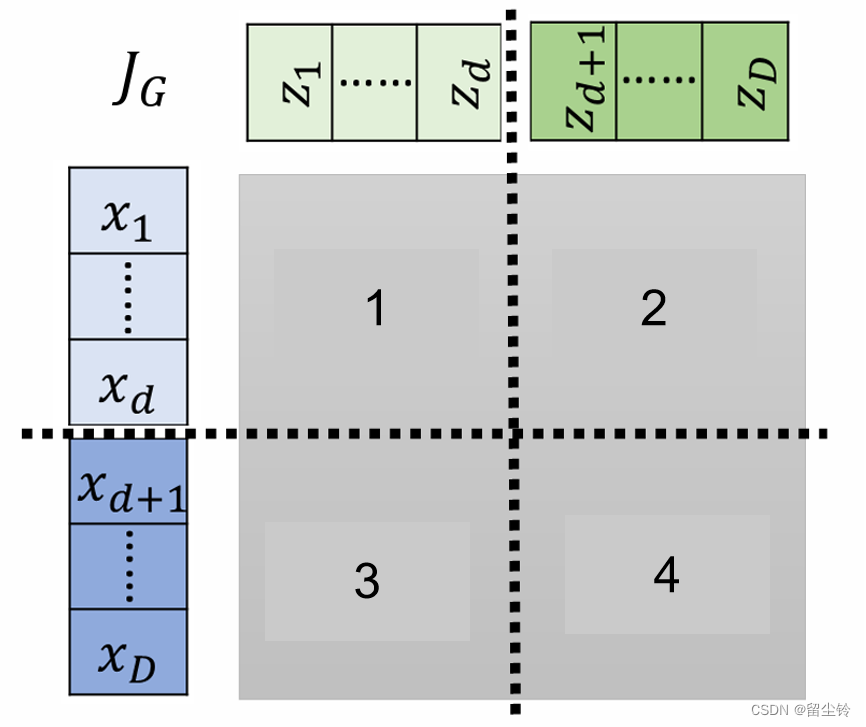
我们不难发现，不同列的分母组合在一起就是输入，不同行的分子组合在一起就是输出。按照雅可比矩阵的写法，我们也可以将耦合层设计的 G 的雅可比矩阵用同样的方式进行排列，将输入摆在上面，将输出摆在侧面。由于之前我们将输入 z 和输出 x 都分成了两部分，因此我们的雅可比矩阵也可以横竖划分成四大块：
- 我们首先来看第一块：第一块是直接复制过去的，因此我们不难推断出，这一部分输入的每一维度对输出的每一维度分别偏微分，最终的结果就是单位矩阵 I。
- 其次是第二块，第二块中，由于 x 的前 d 维完全是由 z 的前 d 维所决定的，和 z 的 d+1~D 维度没有任何关系，反映到这一部分的微分结果就是零矩阵。
- 再然后是第三块。纵使第三块可能会很复杂，但是对于我们来说，第三块有用吗？没用！线性代数的拉普拉斯定理告诉我们，计算矩阵行列式时，在图中，如果出现第一块是单位矩阵，第二块是零矩阵，则其行列式的值就是第四块行列式的值！
- 最后是第四块，如果我们把这个部分的行列式求出来，那整个矩阵的行列式就迎刃而解了。而这一部分中，输出的每一个维度 x_i 都只和输入的对应维度 z_i 相关，因此这一块的矩阵是一个对角矩阵（Diagonal Matrix）！而对角矩阵的行列式值，就是对角线上的所有元素相乘。
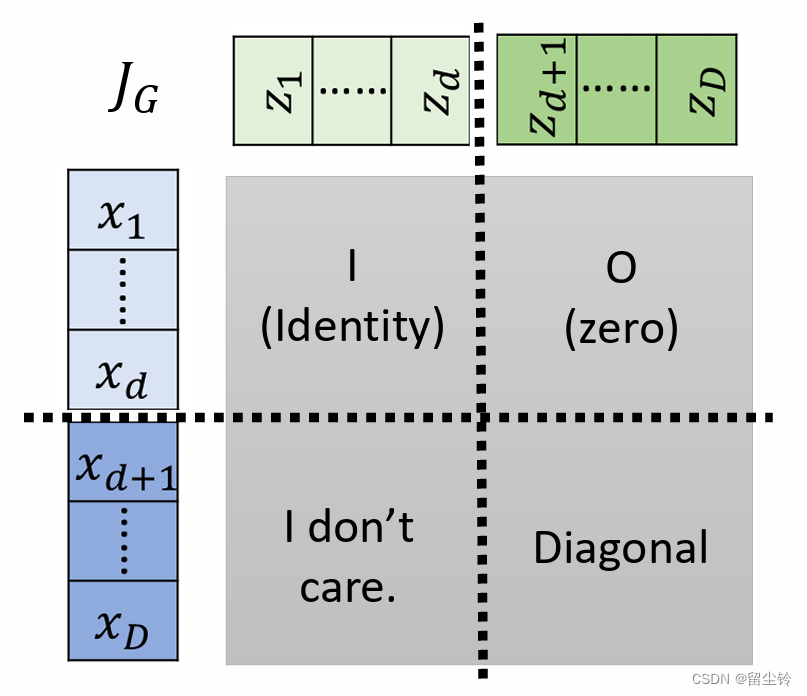
整理上面的结论，我们就可以得到完整的雅可比矩阵：
而其行列式的值我们也可以写出，就是第四部分（右下角）矩阵的行列式的值，根据公式

$x_{i>d} = \beta_i z_i + \gamma_i$

可以求出 G 的雅可比矩阵的行列式为：

$\begin{aligned} \det{(J_G)} &= \frac{\partial x_{d+1}}{\partial z_{d+1}}\frac{\partial x_{d+2}}{\partial z_{d+2}}\cdots\frac{\partial x_{D}}{\partial z_{D}} \\ &=\beta_{d+1}\beta_{d+2}\cdots\beta_{D} \end{aligned}$

耦合层的堆叠

讲完了单个 G 的巧妙的耦合层设计，接下来就需要将多个 G 级联在一起了，也就是需要将多个耦合层堆叠起来。但我们一旦将刚刚介绍的耦合层堆叠起来，我们就能发现一个问题：

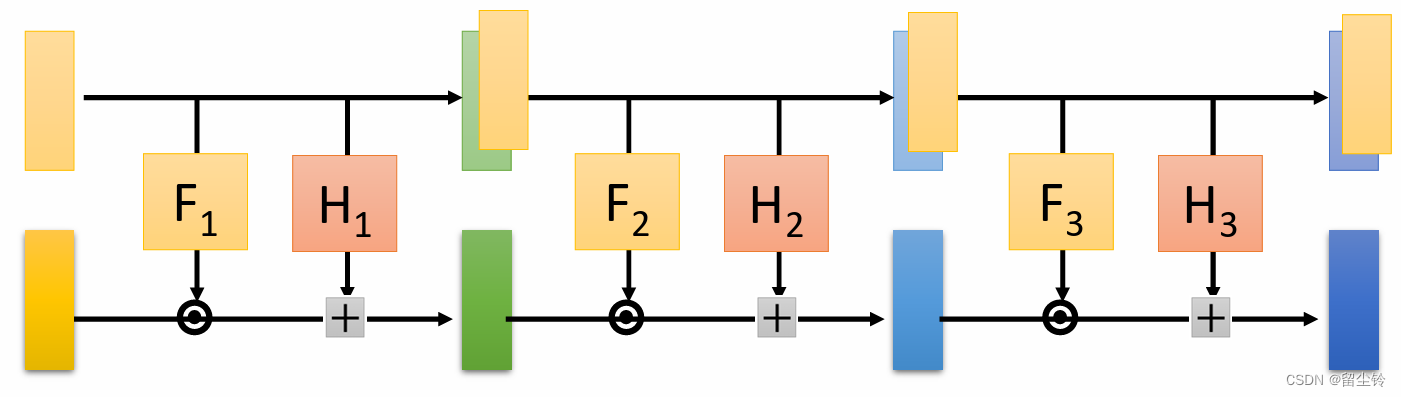
如果按照这样一直堆叠下去，那上半部分不就一直从开头复制到结尾了吗？
这样下来，很有可能生成的图像有一半都是纯高斯噪声，而另一半才有图像，这一点我们是绝对不想看到的。所以在堆叠的时候，我们通常会简单做一些手脚，如：两部分交替复制：
在这种情况中，第一次复制的是上半部分，第二次复制的是下半部分，如此交替。由此一来便可以避免之前的情况。而在实际图像生成中，我们也可以通过像素排列位置、图像通道等方法进行切割和决定哪一部分需要复制，当然，也可以多种分割方式混着用。

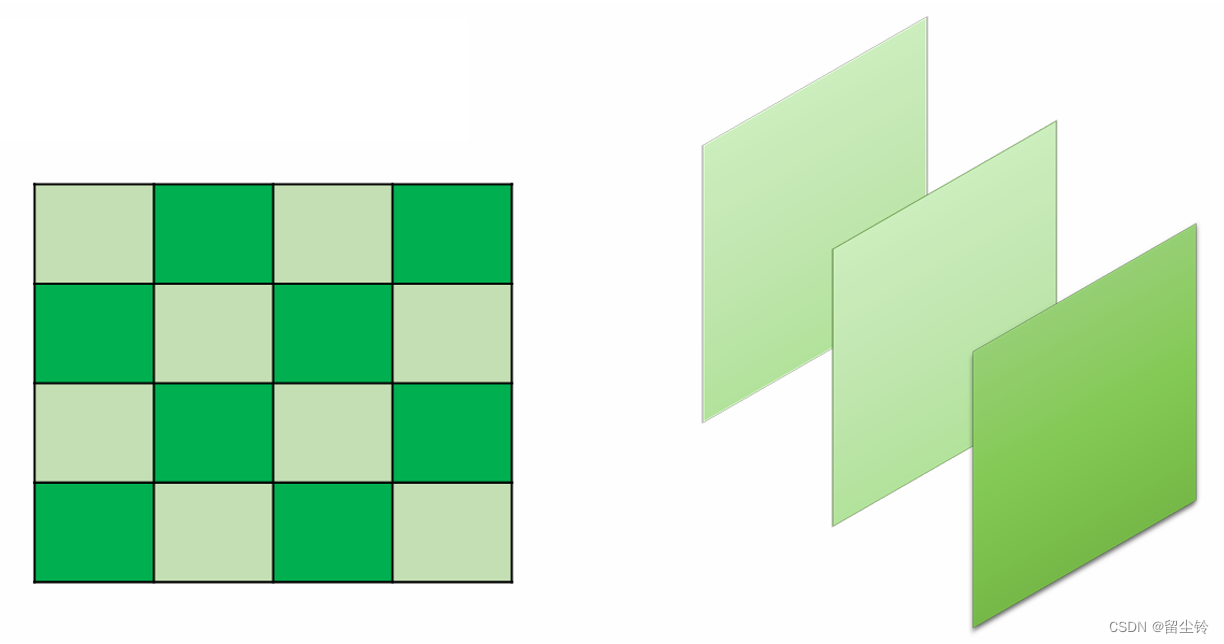
补充：1×1 卷积（1×1 Convolution）

在一个知名的使用 Flow 的模型 GLOW 中，除了耦合层的使用以外，还使用了1×1卷积层。我们知道，图像一般都有 RGB 三个通道，而在 GLOW 中，就使用了这样一个 1×1 的卷积层，每次都选取在同一个位置上的三个通道的像素，经过一个 3×3 的卷积核 W，再到输出图像的同一个位置。
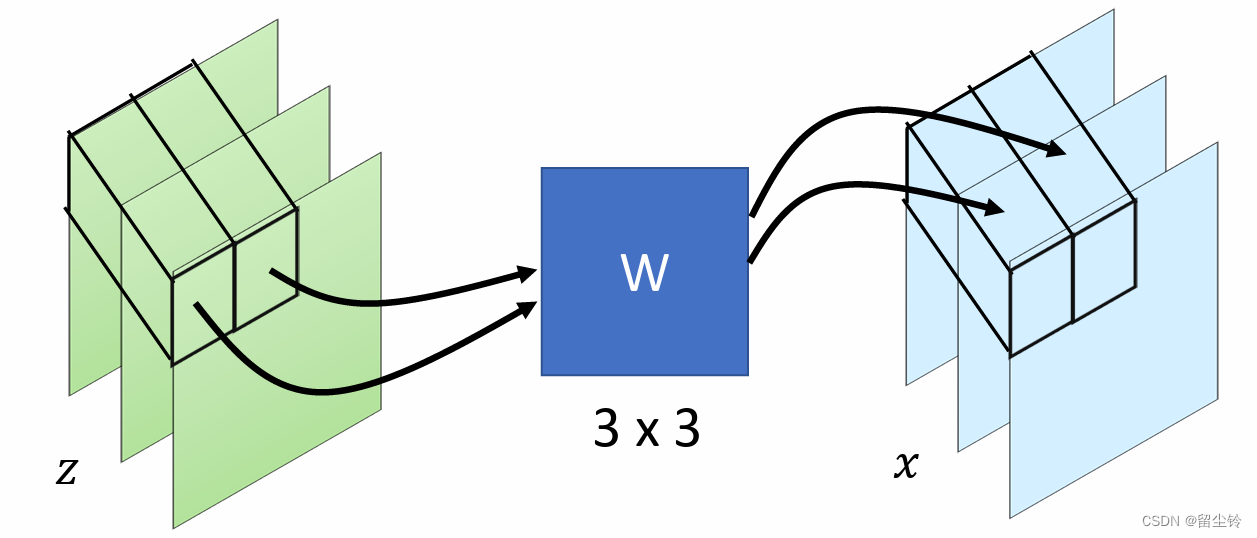
而这样做的好处就是可以起到打乱通道（Shuffle the channel）的作用。就比如我们曾经说，如果耦合层一直复制的是同样一个部分，那到最后这部分就会变成一开始的纯噪声。而如果添加了这样的 1×1 卷积层后，我们就不用担心这种情况了，因为 1×1 卷积层会在合适的时机对通道进行打乱，所以我们可以放心地让耦合层一直复制同一个通道。
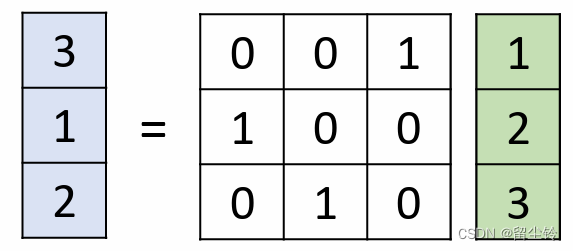
举例来说，如果最后学习到的 W 为下面这样：

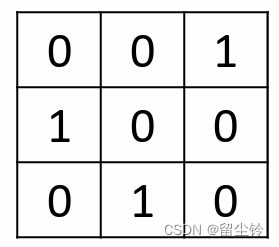
那么在原本 1、2、3 通道排序的像素点经过这样的卷积核后，顺序就变成了这样：
怎么样，是不是非常巧妙？不过既然采用了 1×1 的卷积层，那相当于它也属于 G 的一部分了，所以 W 必须满足我们之前提出的条件。
- 首先，W 可逆吗？如果 W 是一个可逆矩阵，那它就一定是可逆的（？）它是个 3×3 的矩阵，如果可逆，那么它的逆矩阵也非常好计算，带公式就行。问题是 W 是靠神经网络学习出来的，最后的结果一定是可逆的吗？很可惜，GLOW 论文并没有对这个问题做出说明，它只是在初始化时让 W 可逆。我们只能祈祷最后学习出来的 W 是可逆的了。幸运的是，实际上我们随机生成一个 3×3 矩阵，它一般都是可逆的。
- 其次，W 的雅可比矩阵的行列式好计算吗？我们来看一般形式的 W，它长这样：
  
  我们去尝试单独计算它的雅可比矩阵，你会发现：
  
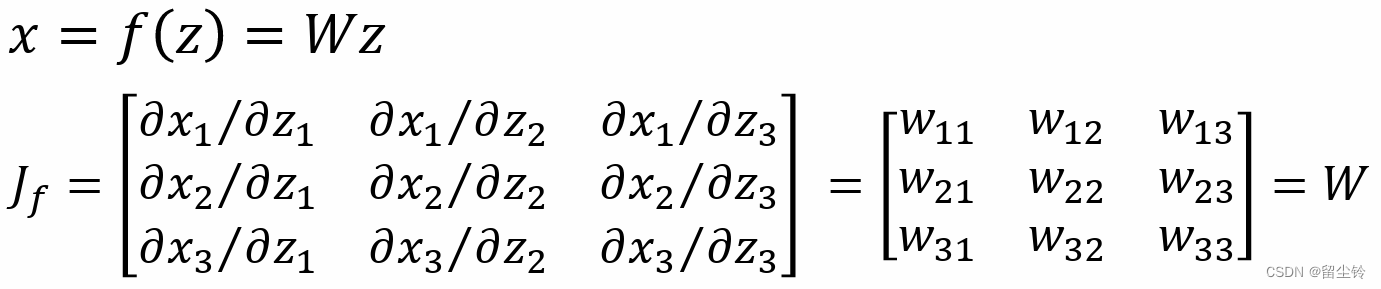
  它的雅可比矩阵就是它自己！而在训练过程中，所有的像素都需要进行卷积，我们把所有的像素铺展开来，整个卷积操作的雅可比矩阵就长这样：
  
  只有同样位置的输入输出的像素向量才会有关系，又因为 W 的雅可比矩阵就是它自己，因此它的雅可比矩阵就是上面这样，W 矩阵在对角线上排布。而它的行列式的值，就是：
  
  $\det(J_C) = (\det (W))^{d*d}$
  
  而 W 就是一 3×3 的矩阵，它的行列式非常好计算，因此整个卷积层的雅可比矩阵的行列式就非常好计算了，这样的操作满足我们给出的限制条件！

Flow 的应用

OpenAI 曾经根据 GLOW 做过一些 Demo，Demo 网址：Glow: Better reversible generative models (openai.com)我们在这里给出 Demo的一些功能和简单的原理。以下部分图片可能会引起不适，请谨慎观看！

人脸混合

将一个人脸通过 G 逆输出成 z1，另一个人脸通过 G 逆输出成 z2，然后 z1 与 z2 取平均，平均值再通过 G，就可以得到混合后的人脸：

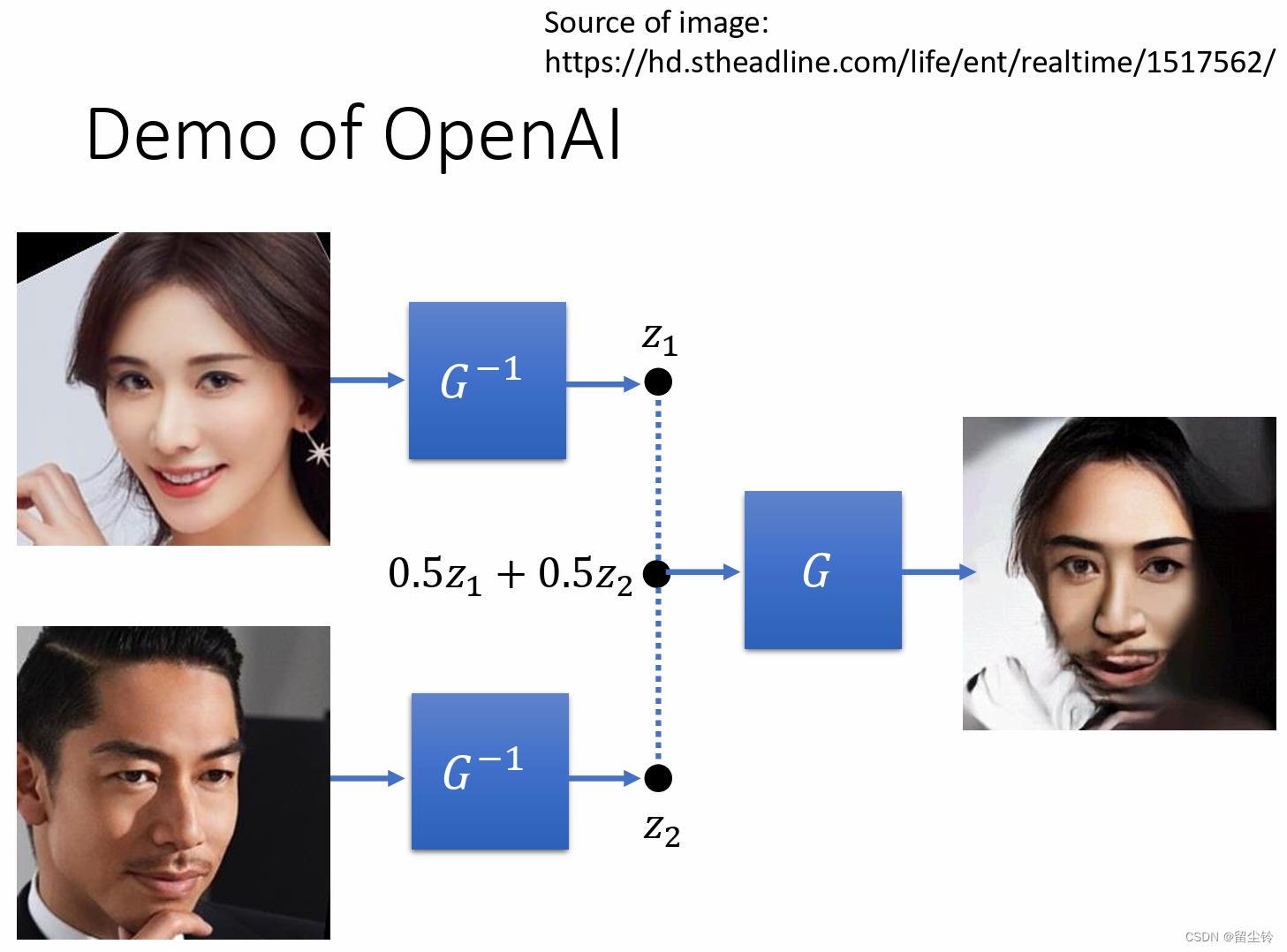
表情改变

怎么让一张不笑的人脸笑起来呢？我们收集一堆不笑的脸的图像，然后再收集一堆笑的脸的图像，把不笑脸的 z 计算出来取平均，把笑脸的 z 计算出来取平均，做差！然后你就能知道，在 z 的空间内，往哪个方向移动，最终输出的人脸是往”笑“的方向走的.

语音合成

虽然 GAN 在图像生成领域大杀四方，Flow 也无法匹敌，然而在语音合成领域中，GAN 的结果却不尽如人意。不过基于 Flow 模型魔改的 WaveGlow 却表现不错，这里贴出相关论文：
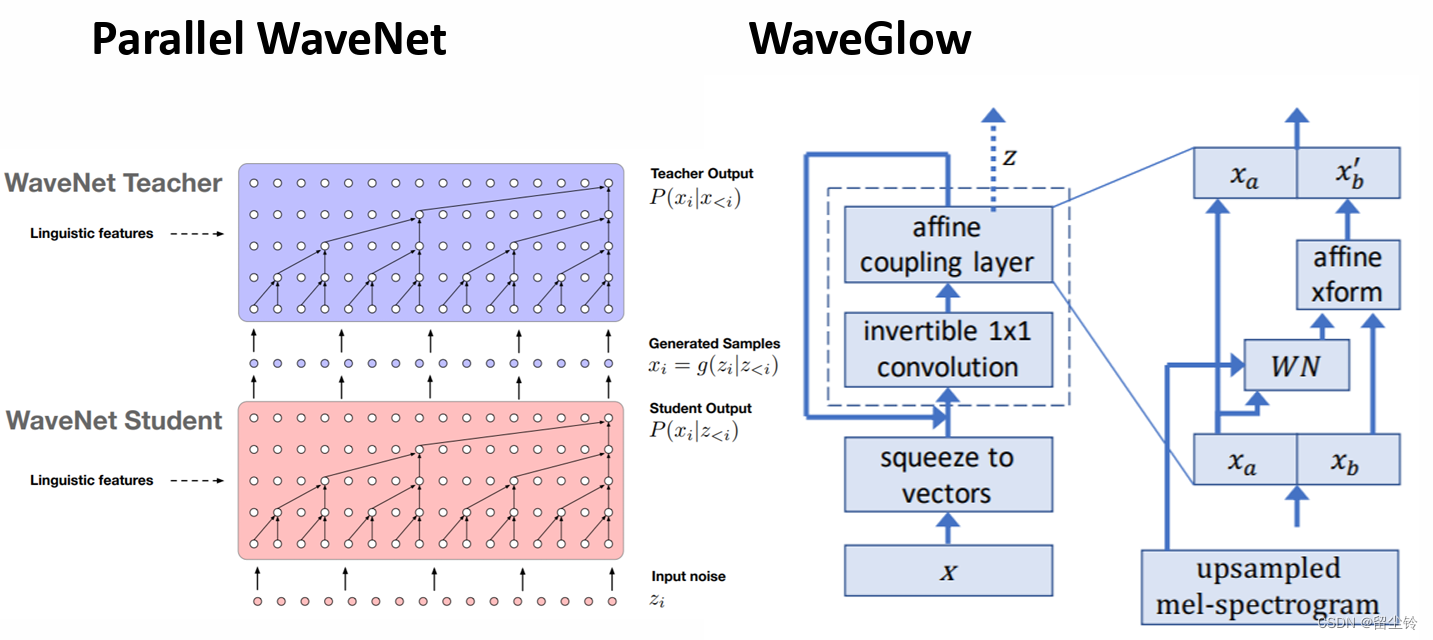
- [1711.10433] Parallel WaveNet: Fast High-Fidelity Speech Synthesis (arxiv.org)
- [1811.00002] WaveGlow: A Flow-based Generative Network for Speech Synthesis (arxiv.org)
我在一篇讲声码器的个人博客里对 WaveGlow 也做了简单的介绍，也欢迎大家前往查看。文章地址：Vocoder，声码器详解——语音信号处理学习（十）_音乐的vocoder模型-CSDN博客

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/AllinToyou/article/detail/379784