AcWing 788. 逆序对的数量——算法基础课题解

AcWing 788. 逆序对的数量

题目描述

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i<j且 a[i]>a[j]，则其为一个逆序对；否则不是。

输入格式

第一行包含整数 n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

数据范围

1≤n≤100000，

数列中的元素的取值范围 [1,10^9]。

输入样例：

6
2 3 4 5 6 1
1
2

输出样例：

5
1

思路

用int会爆内存!

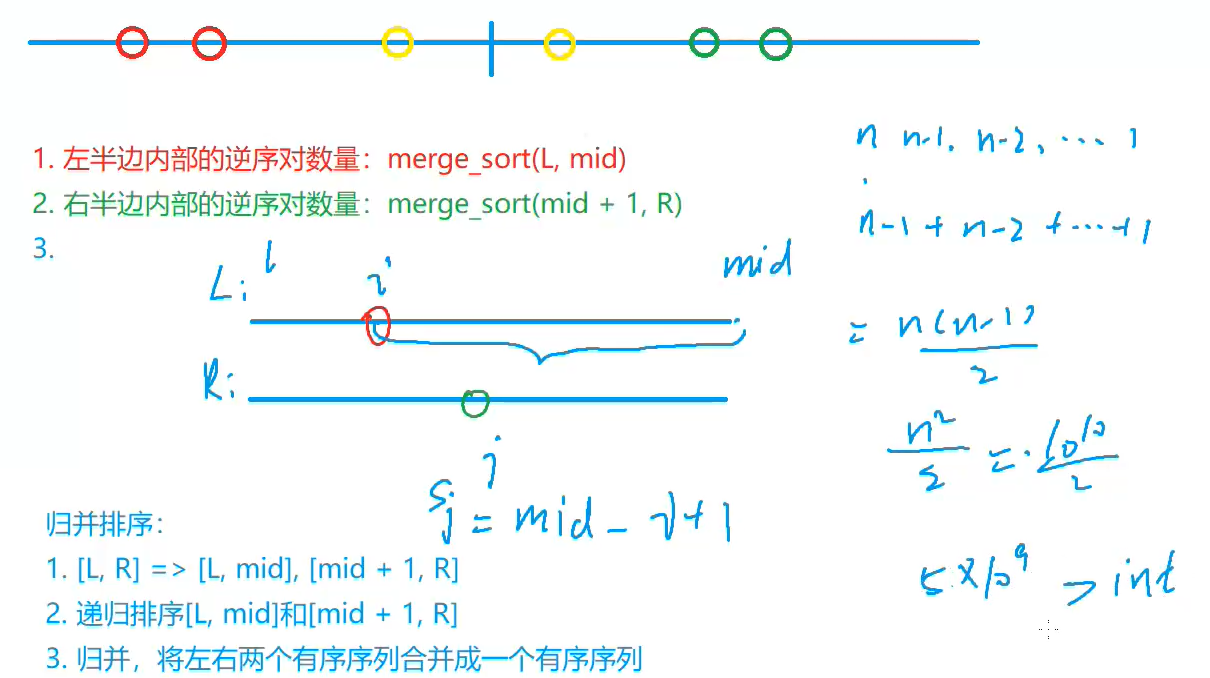
C++

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int tmp[N];

typedef long int L;

L merge_sort(int q[], int l, int r) {
    if (l >= r) return 0;
    int mid = (l + r) >> 1;
    L res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r) {
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else res += mid - i + 1, tmp[k++] = q[j++];
    }
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    for (i = l; i <= r; i++) q[i] = tmp[i - l];
    return res;
}

int main() {
    int n;
    cin >> n;
    int q[N];
    for (int i = 0; i < n; i++) cin >> q[i];
    cout << merge_sort(q, 0, n - 1) << endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

Go

package main

import "fmt"

const N = 1e5 + 10

var tmp = make([]int, N)

func mergeSort(arr []int, l, r int) int64 {
	if l >= r {
		return 0
	}
	mid := (l + r) >> 1
	res := mergeSort(arr, l, mid) + mergeSort(arr, mid+1, r)
	k := 0
	i := l
	j := mid + 1
	for i <= mid && j <= r {
		if arr[i] <= arr[j] {
			tmp[k] = arr[i]
			i++
		} else {
			res += int64(mid - i + 1)
			tmp[k] = arr[j]
			j++
		}
		k++
	}
	for i <= mid {
		tmp[k] = arr[i]
		i++
		k++
	}
	for j <= r {
		tmp[k] = arr[j]
		j++
		k++
	}
	for i := l; i <= r; i++ {
		arr[i] = tmp[i-l]
	}
	return res
}

func main() {
	var n int
	fmt.Scanf("%d", &n)
	arr := make([]int, N)
	for i := 0; i < n; i++ {
		fmt.Scanf("%d", &arr[i])
	}
	fmt.Println(mergeSort(arr, 0, n-1))
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

模板

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18