蓝桥杯刷题总结

一、字串排序

标签：动态规划 2020 省赛

题目描述

小蓝最近学习了一些排序算法，其中冒泡排序让他印象深刻。

在冒泡排序中，每次只能交换相邻的两个元素。

小蓝发现，如果对一个字符串中的字符排序，只允许交换相邻的两个字符，在所有可能的排序方案中，冒泡排序的总交换次数是最少的。

例如，对于字符串 lan 排序，只需要 1 次交换。对于字符串 qiao 排序，总共需要 4 次交换。

小蓝的幸运数字是 VV，他想找到一个只包含小写英文字母的字符串，对这个串中的字符进行冒泡排序，正好需要 VV 次交换。请帮助小蓝找一个这样的字符串。如果可能找到多个，请告诉小蓝最短的那个。如果最短的仍然有多个，请告诉小蓝字典序最小的那个。请注意字符串中可以包含相同的字符。

输入描述
输入一行包含一个整数 V\ (1 \leq V \leq 10^4)V (1≤V≤10
4
)，为小蓝的幸运数字。

输出描述
输出一个字符串，为所求的答案。

输入输出样例

示例1

输入
4
输出
bbaa

示例2

输入
100
输出
jihgfeeddccbbaa

解题思路

首先，题目中要求的是找到一个只包含小写英文字母的字符串，恰好需要V次交换，如果找到了，返回最短的那个，如果最短的存在多个，则返回字典序最小的那个。注意：字符串中可以包含相同的字符。
一般来说：限制的最小得极限条件就是解题思路。对于冒泡排序而言，在最短的字符串中拥有尽可能大的交换次数，这个时候就应该考虑到冒泡排序的最差情况——逆序排序。
其逆序排序的情况下——时间复杂度为O(n^2)。同时实际交换的次数计算如下(n * (n-1))/2。
对于没有重复元素而言为n*(n-1)/2，而对于存在重复元素而言。
例：jihgfeeddccbbaa
j 沉到底需要交换 14次 — ihgfeeddccbbaa j
i 沉到底需要交换 13次 — hgfeeddccbbaaij
…
以此类推
到 eeddccbbaafghij
此时开始
两个ee 沉到底 分别为 8次 — ddccbbaaeefghij
两个dd沉到底 分别为 6次 — ccbbaaddeefghij
由此可见重复元素的交换次数是一致的。

相比于无重复元素，有重复元素的交换次数为n*(n-1)/2 + 重复元素的个数。

解题代码如下：

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int V = in.nextInt();
        //首先排除边界条件
        if(V < 1 || V > 10000) return;
        //计算出在无重复元素下所需的元素个数
        int n = (int) Math.ceil((1+Math.sqrt(1+8*V))/2);
        //求出需要重复元素的个数
        int k = n*(n-1)/2-V;
        //用于保存无重复元素的string字符串
        StringBuffer sb1 = new StringBuffer();
        //作为返回的结果
        String sb2 = "";

        //记录所有元素
        for(int j = n-1; j>=0 ;j--) {
            sb1.append((char)('a'+j));
        }

        int count=0;
        for(int j=n-1; j>=0 ;j--) {
            // 满足n长度条件，则结束
            if(sb2.length() == n) break;
            // 首先先将重复元素放入字符串中
            if(++count<=k) sb2 = ""+sb1.charAt(j) + sb1.charAt(j) +sb2;
            // 将剩下的元素放入字符串中
            else sb2 = ""+sb1.charAt(j)+sb2;
        }
        System.out.println(sb2);
        in.close();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

二、数字三角形

题目描述

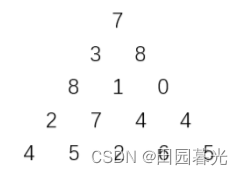
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。

路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右 边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过 1。

输入描述

输入的第一行包含一个整数 N\ (1 \leq N \leq 100)N (1≤N≤100)，表示三角形的行数。

下面的 NN 行给出数字三角形。数字三角形上的数都是 0 至 100 之间的整数。

输出描述

输出一个整数，表示答案。

输入输出样例

示例

输入

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
copy
输出

27
copy

运行限制

最大运行时间：1s
最大运行内存: 256M

解题思路

首先，在路径上面的数加起来可以得到一个和，我们的任务就是找到最大的和。很明显的属于动态规划问题，所以按照动态规划的解题思路，我们只需要找到边界条件和动态转移方程式就行。但是同时题目中增加了一个附加条件，要求，向左下走的次数与向右下走的次数相差不能超过1。这就是求出此题解的重要条件。
试想要满足相差次数小于等于1，那么三角中边界的数字为路径尾部的情况就会被排除掉。同样，最终的结果必然在奇数列的中心产生，或者偶数列中中心两个数字中的一个产生，如此就可以求出解。

解题代码如下：

import java.util.Scanner;

public class Main {

    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        int line = scanner.nextInt();
        # 用于保存原始数据的数组
        int[][] triangle = new int[line][line];
        # 用于保存动态转移路径的数组，其中dp[n][m]表示到triangle中第n行m列数字为结尾的最大路径值。
        int[][] dp = new int[line][line];
        for(int i = 0;i < line;i++) {
            for(int j = 0; j <= i;j++) {
                triangle[i][j] = scanner.nextInt();
            }
        }
        scanner.close();
        System.out.println(findMaxSum(triangle, dp, line));
    }

    public static int findMaxSum(int[][] triangle, int[][] dp, int line) {
        # 给左边界赋予初值
        dp[0][0] = triangle[0][0];
        for(int i = 1;i < line; i++) {
            dp[i][0] = dp[i-1][0] + triangle[i][0];
        }
        # 根据动态转移方程式求解
        for(int i=1;i<line;i++) {
            for(int j = 1;j <=i;j++) {
                dp[i][j] = triangle[i][j] + Math.max(dp[i-1][j], dp[i-1][j-1]);
            }
        }

        # 通过判断奇偶行来求解
        if(line % 2 != 0) {
            return dp[line-1][line / 2];
        } else {
            return Math.max(dp[line-1][line/2], dp[line-1][line/2 - 1]);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

三、青蛙过河

问题描述

小青蛙住在一条河边, 它想到河对岸的学校去学习。小青蛙打算经过河里 的石头跳到对岸。

河里的石头排成了一条直线, 小青蛙每次跳跃必须落在一块石头或者岸上。 不过, 每块石头有一个高度, 每次小青蛙从一块石头起跳, 这块石头的高度就 会下降 1 , 当石头的高度下降到 0 时小青蛙不能再跳到这块石头上（某次跳跃 后使石头高度下降到 0 是允许的)。

小青蛙一共需要去学校上 xx 天课, 所以它需要往返 2 x2x 次。当小青蛙具有 一个跳跃能力 yy 时, 它能跳不超过 yy 的距离。

请问小青蛙的跳跃能力至少是多少才能用这些石头上完 xx 次课。

输入格式

输入的第一行包含两个整数 n, xn,x, 分别表示河的宽度和小青蛙需要去学校 的天数。请注意 2 x2x 才是实际过河的次数。

第二行包含 n-1 个非负整数 H1, H2,…, Hn-1, 其中 Hi >0 表示在河中与 小青蛙的家相距 ii 的地方有一块高度为 Hi 的石头, Hi =0 表示这个位置没有石 头。

输出格式

输出一行, 包含一个整数, 表示小青蛙需要的最低跳跃能力。

样例输入

5 1
1 0 1 0

样例输出

4

样例说明

由于只有两块高度为 11 的石头，所以往返只能各用一块。第 11 块石头和对岸的距离为 44，如果小青蛙的跳跃能力为 33 则无法满足要求。所以小青蛙最少需要 44 的跳跃能力。

运行限制

最大运行时间：1s
最大运行内存: 512M

解题思路

对于这个问题，需要将其抽象为数学问题，如果只是简单的模拟，肯定无法满足用户规模与约定的限制。
首先对于要求出的最小步数，我们假设其跳跃能力为y，而当前起跳位置为i，则区间在[i,i+y]内，无论怎样进行跳跃，一共进行的2x次跳跃，都必须落在这个区间中。根据满足这个充分条件，我们可以求出最小y值。

解题代码

import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int width = scanner.nextInt();
        long days = scanner.nextInt();
        long[] ori_bones = new long[width+1];
        for (int i = 1; i < width; i++) {
            # 采用累和数组来记录，方便后面进行区间计算。
            ori_bones[i] = scanner.nextInt() + ori_bones[i - 1];
        }
        # 岸边值设置极大值。
        ori_bones[width] = ori_bones[width - 1] + 9999999999L;
        int l = 0;
        int sum = 0;
        # 逐步遍历区间[l,j],求出对于任意区间[l,j]都满足充分条件的步数最小值。
        for (int j = 1; j <=width; j++) {
            if (ori_bones[j] - ori_bones[l] >= 2L * days) {
                sum = Math.max(sum, j - l);
                l += 1;
            }
        }
        System.out.println(sum);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

四、求和

问题描述

给定n个整数a1,a2,…,an, 求它们两两相乘再相加的和，即：
S = a1a2 + a1a3 + … + a1an + a2 * a3 + an-2an-1 + an-2 an + an-1an

输入格式

输入的第一行包含一个整数n。
第二行包含n个整数a1，a2，…,an。

输出格式

输出一个整数S，表示所求的和。请使用合适的数据类型进行运算。

样本输入

4
1 3 6 9
1
2

样例输出

117
1

评测用例规模与约定

对于30%的数据，1≤n≤1000，1≤ai≤100。
对于所有评测用例，1≤n≤200000，1≤ai≤1000。

运行限制

• 最大运行时间：1s
• 最大运行内存：512M

解题思路

首先这个题属于简单范畴，只需要按照题目中所给公式求和就行，但是注意：评测用例规模与约定，其中n和ai的所有评测用例值就很大，所以首先排除暴力的双重循环O(n^2)。那么就要想办法将解题的时间复杂度降低为O(n)(这里是线性直觉…)，然后重新看题目
S = a1a2 + a1a3 + … + a1an + a2 * a3 + an-2an-1 + an-2 an + an-1an
根据结合律可以变为：
S = a1*(a2+…+an) + an-2*(an-1 + an) + an-1 *an;
即为式子1：

可见O(n)的时间复杂度的计算式已经被提取出来了，那么剩下的问题就是解决式子2。

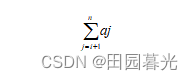
在这里就可以用差分思想，用数组保存a1 , a1+a2 , … ，a1+a2+…+an的值，便于通过 (a1+…+aj+…+an) - (a1+…+aj-1)直接求解式子2。

解题代码

import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int Num = scanner.nextInt();
        long[] arr = new long[Num+1];
        long[] arrSum = new long[Num+1];
        for(int i = 1;i <= Num;i++){
            arr[i] = scanner.nextInt();
            arrSum[i] = arr[i] + arrSum[i-1];
        }
        System.out.println(returnSumFormArr(Num, arr, arrSum));
    }
    
    private static long returnSumFormArr(int Num, long[] arr, long[] arrSum) {
        long sum = 0;
        for(int i = 1; i<= Num;i++) {
            sum += arr[i] * (arrSum[Num] - arrSum[i]);
        }
        return sum;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

五、刷题统计

问题描述

小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做a道题目，周六和周日每天做b道题目。请你帮小明计算，按照计划他将在第几天实现做题数大于等于n题？

输入格式

输入一行包含三个整数a,b和n。

输出格式

输出一个整数代表天数。

样例输入

10 20 99
1

样例输出

8
1

评测用例规模与约定

对于50%的评测用例，1≤a,b,n≤10^6.
对于100%的评测用例，1≤a,b,n≤10^18.

运行限制

• 最大运行时间：1s
• 最大运行内存

解题思路

私以为这道题算是比较简单类的，思路也比较容易想到。只需要考虑100%评测用例的范围，运行时间的效率就好。那么首先就是缩短时间，那么就肯定不能一个一个逐个递增的while循环，最好可以一步到位，或者一步到位的附近。那么我们只需要做个小小的除法运算就行。

解题代码

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        long a = scanner.nextLong();
        long b = scanner.nextLong();
        long n = scanner.nextLong();
        System.out.println(findDays(a,b,n));
    }

    private static long findDays(long a, long b, long n) {
        long days = (n / (5*a + 2*b)) * 7;
        long sumP = (n / (5*a + 2*b)) * (5*a + 2 *b);
        while(sumP < n) {
            days += 7;
            sumP += (5*a+2*b);
        }
        if(sumP == n) {
            return days;
        } else if(sumP > n) {
            int w = 0;
            while(sumP > n) {
                if(w < 2) {
                    sumP -= b;
                    days--;
                    w++;
                } else {
                    sumP -= a;
                    days--;
                }
            }
        }
        return sumP == n? days : days + 1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

六、李白打酒加强版

问题描述

话说大诗人李白, 一生好饮。幸好他从不开车。

一天, 他提着酒显, 从家里出来, 酒显中有酒 2 斗。他边走边唱:

无事街上走，提显去打酒。 逢店加一倍, 遇花喝一斗。

这一路上, 他一共遇到店 NN 次, 遇到花 MM 次。已知最后一次遇到的是花, 他正好把酒喝光了。

请你计算李白这一路遇到店和花的顺序, 有多少种不同的可能?

注意: 显里没酒 ( 0 斗) 时遇店是合法的, 加倍后还是没酒; 但是没酒时遇 花是不合法的。

输入格式

第一行包含两个整数N和M

输出格式

输出一个整数表示答案。由于答案可能很大，输出模 1000000007 的结果.

样例输入

5 10
1

样例输出

14
1

评测用例规模与约定

对于 40 %40% 的评测用例: 1 \leq N, M \leq 101≤N,M≤10 。

对于 100 %100% 的评测用例: 1 \leq N, M \leq 1001≤N,M≤100 。

运行限制

最大运行时间：1s
最大运行内存：256M

解题思路

对于这道题，第一感觉就是每一轮遇见花或者店后，酒的数量变化是都依赖于上一轮的，且每一轮都是可以拆分成子单元进行求解的，感觉深度优先遍历DFS和动态规划都是可以实现的。遂对着DFS一顿操作猛如虎，果不其然超时。

import java.util.Scanner;
public class Main {
    private static final int mod = (int)1e9+7;
    private static long allPath = 0;
    private static int N = 0;
    private static int M = 0;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        N = scanner.nextInt();
        M = scanner.nextInt();
        System.out.println(pathNum(N, M));
    }
    private static long pathNum(int N, int M) {
        int wine = 2;
        int i = 0;
        // 初始情况下：第一次可能遇见花，也可能遇见店
        nodes(wine, 0, i, 0, 0);
        nodes(wine, 1, i, 0, 0);
        return allPath % mod;
    }
    private static int nodes(int wine, int nextState,int line, int NState, int MState) {
        // 边界条件
        if(wine < 0 || line >= (N + M) || NState > N || MState > M) {
            return -1;
        }
        // 特殊情况：没酒时遇 花是不合法的
        if(wine <= 0 && nextState == 0) {
            return -1;
        }
        // 如果遇见的是花
        if(nextState == 0) {
            wine -= 1;
            MState++;
        } else if(nextState == 1){ // 如果遇见的是店
            wine *= 2;
            NState++;
        }
        line++;
        // 最后一轮遇到的是花，他正好把酒喝光了
        if(line == (N + M -1) && N == NState) {
            MState++;
            wine--;
            line++;
            if(wine == 0 && MState == M) {
                allPath++;
                return -1;
            }else{
                return -1;
            }
        }
        // DFS 下一轮可能遇见花或酒
        nodes(wine, 0, line, NState, MState);
        nodes(wine, 1, line, NState, MState);
        return wine;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

测试几把后，察觉到事情不对起来，仔细看题，实际上评测用例规模和约定，已经提示的很明显了，按照DFS的遍历步骤肯定无法达标，直接用动态规划的思路来求解。
题目中，一共出现了三种动态变量，遇花，遇店，剩余酒的量。其中，花和店的数量都是明确确定的，而酒的量的变化根据这两者而变化。而题目中要求最后一次必须是遇花喝酒，那么酒的量肯定是不能超过遇花的次数的。所以我们采用三维dp数组用dp[N][M][M]来表示，该数组表示遇见了n个店、m次花和剩下的酒的数量。而最后一次必须是遇花喝酒，所以最终答案是：dp[n][m-1][1]。
回到动态规划方程式上，我们可以知道当还有偶数酒的时候，上一次可能是遇见了花喝了一杯，也可能是遇见了店翻了一番。当还有奇数酒的时候，只能是遇见了花喝了一杯。

解题代码

import java.util.Scanner;
public class Main {
    public static final int mod = (int)1e9+7;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n=scan.nextInt();
        int m=scan.nextInt();
        int[][][] dp = new int[n+1][m+1][m+5];
        dp[0][0][2]=1;
        dp[0][1][1]=1;
        dp[0][2][0]=1;
        for(int i=1;i<=n;i++){
          for(int j=0;j<=m;j++){
            for(int k=0;k<=m;k++){
              if(k%2==0){
                if(j>0)  dp[i][j][k]+=dp[i][j-1][k+1];
                if(i>0)  dp[i][j][k]+=dp[i-1][j][k/2];
              }
              else{
                if(j>0) dp[i][j][k]+=dp[i][j-1][k+1];
              }
              dp[i][j][k]%=mod;
            }
          }
        }
        System.out.println(dp[n][m-1][1]%mod);
        scan.close();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

七、数位排序

问题描述

小蓝对一个数的数位之和很感兴趣, 今天他要按照数位之和给数排序。当 两个数各个数位之和不同时, 将数位和较小的排在前面, 当数位之和相等时, 将数值小的排在前面。

例如, 2022 排在 409 前面, 因为 2022 的数位之和是 6, 小于 409 的数位 之和 13 。

又如, 6 排在 2022 前面, 因为它们的数位之和相同, 而 6 小于 2022 。

给定正整数 n, mn,m, 请问对 1 到 nn 采用这种方法排序时, 排在第 mm 个的元 素是多少?

输入格式

输入第一行包含一个正整数 nn 。

第二行包含一个正整数 mm 。

输出格式

输出一行包含一个整数, 表示答案。

样例输入

13
5

样例输出

3

解题思路

这是一个桶排序问题，只需要从头遍历，将每个元素依次放入其sum对应的桶中即可，为了保持从小到大的顺序，可以采用Map<Integer, List> 来保存。

解题代码

import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        Map<Integer, List<Integer>> record = new HashMap<>();
        for(int i = 1; i<=n;i++) {
            int sum = calSum(i);
            List<Integer> temp = new LinkedList<>();
            if(record.containsKey(sum)){
                temp = record.get(sum);
                temp.add(i);
                record.put(sum, temp);
            } else {
                temp.add(i);
                record.put(sum,temp);
            }
        }
        for(Integer elemet : record.keySet()) {
            if( m > record.get(elemet).size()) m -= record.get(elemet).size();
            else {
                System.out.println(record.get(elemet).get(m-1));
                return;
            }
        }
    }

    private static int calSum(int num) {
        int sum = 0;
        while(num > 0) {
            sum += num % 10;
            num /= 10;
        }
        return sum;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

八、蜂巢

题目描述

蜂巢由大量的六边形拼接而成，定义蜂巢中的方向为：0 表示正西方向，1 表示西偏北 60◦，2 表示东偏北 60◦，3 表示正东，4 表示东偏南 60◦，5 表示西偏南 60◦。

对于给定的一点 O，我们以 O 为原点定义坐标系，如果一个点 A 由 O 点先向 d 方向走 p 步再向 (d + 2) mod 6 方向（d 的顺时针 120◦ 方向）走 q 步到达，则这个点的坐标定义为 (d, p, q)。在蜂窝中，一个点的坐标可能有多种。

下图给出了点 B(0, 5, 3) 和点 C(2, 3, 2) 的示意。

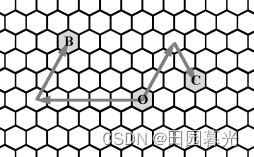
给定点 (d1, p1, q1) 和点 (d2, p2, q2)，请问他们之间最少走多少步可以到达？

输入格式

输入一行包含 6 个整数 d1, p1, q1, d2, p2, q2 表示两个点的坐标，相邻两个整数之间使用一个空格分隔。

输出格式

输出一行包含一个整数表示两点之间最少走多少步可以到达。

样例输入

0 5 3 2 3 2

样例输出

7

解题思路

对于这题，采用模拟思路，通过将六边形网络，以及以O为坐标原点为参考系，将B、C投影到二维坐标系上，然后通过计算出两者的x和y的绝对值来得到步数解。

解题代码

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
      Scanner scanner = new Scanner(System.in);
        double[][] dirs = new double[][]{{-1, 0},
                {-0.5, 1},
                {0.5, 1},
                {1, 0},
                {0.5, -1},
                {-0.5, -1}};
        int a = scanner.nextInt(); long b = scanner.nextLong(); long c = scanner.nextLong();
        int x = scanner.nextInt(); long y = scanner.nextLong(); long z = scanner.nextLong();
        double[] A = new double[2];
        double[] B = new double[2];
        for(int j = 0; j < 2; j++) {
            A[j] += b * dirs[a][j]; 
            B[j] += y * dirs[x][j];
        }
        for(int j = 0; j < 2;j++) {
            A[j] += c * dirs[(a + 2) % 6][j];
            B[j] += z * dirs[(x + 2) % 6][j];
        }
        double m = Math.abs(A[0] - B[0]);
        double n = Math.abs(A[1] - B[1]);
        if ( n * 0.5 >= m) {
            System.out.println((int) n);
        } else {
            System.out.println((int) (m + n * 0.5));
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

九、技能升级

问题描述

小蓝最近正在玩一款 RPG 游戏。他的角色一共有 NN 个可以加攻击力的技能。
其中第 i 个技能首次升级可以提升 Ai 点攻击力, 以后每次升级增加的点数 都会减少 Bi. Ai/Bi 次之后, 再升级该技能将不会改变攻击力。
现在小蓝可以总计升级 MM 次技能, 他可以任意选择升级的技能和次数。请 你计算小蓝最多可以提高多少点攻击力?

输入格式

输入第一行包含两个整数 N 和 M 。
以下 NN 行每行包含两个整数 Ai和Bi

输出格式

输出一行包含一个整数表示答案

样例输入

3 6
10 5
9 2
8 1
1
2
3
4

样例输出

47
1

解题思路

作为平凡人的一份子，首先的想法是贪心模拟，只需要把每轮能够取得的最有分数拿到手就够了，一看评测用例规模和约定，果不其然没有那么简单。苦苦思来想去，毫无头绪，看了看题解：
从二分查找入手，只需要找到第m个元素他的值，作为分割，大于它的值能够出现的分数都能够被选中，小于他的值则不可能被选中。依次为思路在看题就明了。解题代码来自：https://blog.dotcpp.com/a/95141

解题代码

import java.util.Scanner;
public class Main {

    public static long[] power;
    public static long[] lose;

    public static int n;
    public static int m;
    /**
     *
     * 我们能不能找到第m个元素的值num_n，然后在对个每个power依次减去lose，如果发现剩下的power已经小于num_n，说明这个技能完全是不会用上的了。
     */
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        while(input.hasNext()) {
            n = input.nextInt();
            m = input.nextInt();

            power = new long[n];
            lose = new long[n];
            for(int i =0; i < n;i++) {
                power[i] = input.nextLong();
                lose[i] = input.nextLong();
            }
            int left = 0, right = 1000000;
            long num_m = 0;
            while(left <= right) {
                int mid = (left + right) >> 1;
                if(in_right(mid)) { // 说明要找的num_m在mid的右边
                    num_m = mid; // num_m 先记录下来，因为比nun_m 大的元素已经足够m了
                    left = mid + 1;
                } else {
                    right = mid - 1;
                }
            }
            // 此时已经找到了num_m, 他就是第m大的数值
            // 但是我们不知道num_m出现了多少次，可能它一共出现了10次，但是第m个是第三次，如果直接把num_m的个数加上，可能会使得更大的power没有加上。
            long sum = 0;
            long num = 0; // 已经找到的点的个数
            for(int i = 0; i < n;i++) {
                if(power[i] < num_m) continue;
                long k = 0;
                if((power[i] - num_m) % lose[i] == 0) { // 表示num_m也算一个点，但是我们不能算上他
                    k = (power[i] - num_m) / lose[i];
                } else {
                    k = (power[i] - num_m) / lose[i] + 1; // 表示num_m 不算一个点，那么需要+1表示点数
                }
                sum += power[i] * k - lose[i] * ( 0 + (k - 1)) * k/2;
                num += k;
            }
            if (num < m) {
                sum += (m - num) * num_m;
            }
            System.out.println(sum);

        }
    }

    // 假设k为第m大的数字，那么求存在多少数字是 >= k的
    public static boolean in_right(long k) {
        long count = 0;
        for(int i = 0; i < n;i++) {
            if(power[i] < k) {
                continue;
            }
            count += (power[i] - k) / lose[i] + 1; // (power[i]-k)/lose[i] 表示前面有几段，但是需要+1才能表示能加进去的点
        }
        return count >= m;
    }

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

十、最优清零方案

问题描述

给定一个长度为N的数列 A1, A2, A3, …, An. 现在小蓝想通过若干次操作将 这个数列中每个数字清零。

每次操作小蓝可以选择以下两种之一:

选择一个大于 0 的整数, 将它减去 1 ;
选择连续 KK 个大于 0 的整数, 将它们各减去 1 。
小蓝最少经过几次操作可以将整个数列清零?

输入格式

输入第一行包含两个整数N和K。
第二行包含N个整数 A1,A2,A3…, An。

输出格式

输出一个整数表示答案

样例输入

5  2
1 2 0 3 4
1
2

样例输出

6
1

解题思路

模拟思路， 优先进行满足条件二的消减， 减去连续k个大于0的子数组中最小的元素，且该元素不为0， 然后在对剩下的元素逐个消减

解题代码

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
      private static int n, k;
    private static int arr[];

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        k = scanner.nextInt();
        arr = new int[n];
        for(int i = 0; i < n;i++) {
            arr[i] = scanner.nextInt();
        }
        System.out.println(findOptimalCase(n, k, arr));
    }

    private static long findOptimalCase(int n, int k, int[] arr) {
        long count = 0;
        int i = 0;
        while(i < n) {
            if(i + k - 1 < n) {
                int min = findMinInArr(arr,i,i+k);
                if(min != 0) {
                    count += min;
                    for(int j = i; j < i+k;++j) arr[j] -= min;
                }
                // int temp = i;
                // for(int j = temp; j < temp+k;++j) {
                //     if(arr[j] == 0 ) {
                //         i = j;

                //     }
                // }
            }
            i++;
        }
        for(int j = 0; j < n;j++) {
            if(arr[j] != 0) count += arr[j];
        }
        return count;
    }

    private static int findMinInArr(int[] arr, int start, int end) {
        int min = Integer.MAX_VALUE;
        for(int i = start; i < end; ++i) {
            if(arr[i] < min) {
                min = arr[i];
            }
        }
        return min;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55