密码学是一门古老而深奥的学科，对一般人来说是非常陌生的。长期以来，只在很小的范围内使用，如军事、外交、情报等部门。计算机密码学是研究计算机信息加密、解密及其变换的科学，是数学和计算机的交叉学科，也是一门新兴的学科。随着计算机网络和计算机通讯技术的发展，计算机密码学得到前所未有的重视并迅速普及和发展起来。在国外，它已成为计算机安全主要的研究方向。

密码学的历史比较悠久，在四千年前，古埃及人就开始使用密码来保密传递消息。两千多年前，罗马国王Julius Caesare（恺撒）就开始使用目前称为“恺撒密码”的密码系统。但是密码技术直到本20世纪40年代以后才有重大突破和发展。特别是20世纪70年代后期，由于计算机、电子通信的广泛使用，现代密码学得到了空前的发展。

恺撒密码

恺撒密码是一种简单的移位密码，它把字母表中的每个字母用该字母后面的第三个字母来代替。例如“a”将变成“D”，“b”将变成“E”，“c”将变成“F”等。在字母表的最后，移位将重新折回，形成一个循环，“x”将变成“A”，“y”将变成“B”，“z”将变成“C”。能够列出所有可能性定义如下所示的变换：

明码字母表：ABCDEFGHIJKLMNOPQRSTUVWXYZ

密码字母表：DEFGHIJKLMNOPQRSTUVWXYZABC

明文：veni,vidi，vjdj，vici

密文：yhql,ylgl，ymgm,ylfl

现在，为每个字母分配一个数值（如a=0、b=1等），对每个明文字母p，用密文字母C代替，则恺撒密码的加密算法可表示为：

C=E(p)=(p+3)mod 26

p=D(C)=(C-3)mod 26

栅栏密码

栅栏密码：栅栏密码的加密变换规则是首先将明文分成n个字符一栏，一栏为一行构成一个行列式；然后行列式行列转置后按列上下排列字符生成密文。将n=2的栅栏密码称为2栏栅栏密码，要求明文去除空格后长度为偶数。

【例】 p1=there is a cipher，使用2栏栅栏密码加密，求c1

去空格，p1=thereisacipher
2个字符一栏，th，er，ei，sa，ci，ph，er
生成行列式：，矩阵行列转置得
合并，c1=teescpehriaihr。分出空格， c1=teesc pe h riaihr

消息和加密

遵循国际命名标准，加密和解密可以翻译成：“Encipher（译成密码）”和“（Decipher）（解译密码）”。也可以这样命名：“Encrypt（加密）”和“Decrypt（解密）”。消息被称为明文(plainText)。用某种方法伪装消息以隐藏它的内容的过程称为加密，加了密的消息称为密文，而把密文转变为明文的过程称为解密，如图表明了加密和解密的过程

明文用M（Message，消息）或P（Plaintext，明文）表示，它可能是比特流、文本文件、位图、数字化的语音流或者数字化的视频图像等

密文用C（Cipher）表示，也是二进制数据，有时和M一样大，有时稍大。通过压缩和加密的结合，C有可能比P小些

加密函数E作用于M得到密文C，用数学公式表示为：E（M）=C。解密函数D作用于C产生M，用数据公式表示为：D（C）=M。先加密后再解密消息，原始的明文将恢复出来，D（E（M））=M必须成立

密码的三个特性

鉴别：消息的接收者应该能够确认消息的来源，入侵者不可能伪装成他人
完整性：消息的接收者应该能够验证在传送过程中消息没有被修改，入侵者不可能用假消息代替合法消息
抗抵赖性：发送消息者事后不可能虚假地否认他发送的消息

算法和密钥

算法也叫密码函数，是用于加密和解密的数学函数。通常情况下，有两个相关的函数，分别用作加密/解密。若算法本身保密，称之为受限制的算法受限制算法存在一定的缺陷，只有在低密级的应用中，具有一定的价值。

现代密码学用密钥解决了这个问题，密钥用K(Key)表示。K可以是很多数值里的任意值，密钥K的可能值的范围叫做密钥空间。加密和解密运算都使用这个密钥，即运算都依赖于密钥，并用K作为下标表示，加解密函数表达为：

如图所示

有些算法使用不同的加密密钥和解密密钥，也就是说加密密钥K1与相应的解密密钥K2不同，在这种情况下，加密和解密的函数表达式为：

函数必须具有的特性是，DK2（EK1（M））=M，如图所示

对称算法

基于密钥的算法通常有两类：对称算法和公开密钥算法（非对称算法）。对称算法有时又叫传统密码算法，加密密钥能够从解密密钥中推算出来，反过来也成立。在大多数对称算法中，加解密的密钥是相同的。对称算法要求发送者和接收者在安全通信之前，协商一个密钥。对称算法的安全性依赖于密钥，泄漏密钥就意味着任何人都能对消息进行加解密。对称算法的加密和解密表示为：

对称密钥算法可以分为两类：序列算法和分组算法

一次只对明文中的单个比特或者字节进行运算的算法称为序列算法或者序列密码
另一类算法是对明文的一组比特或者字节进行运算，称为分组算法或者分组密码

公开密钥算法

公开密钥算法（非对称算法）的加密的密钥和解密的密钥不同，而且解密密钥不能根据加密密钥计算出来，或者至少在可以计算的时间内不能计算出来，之所以叫做公开密钥算法，是因为加密密钥能够公开，即陌生者能用加密密钥加密信息，但只有用相应的解密密钥才能解密信息。加密密钥叫做公开密钥（简称公钥），解密密钥叫做私人密钥（简称私钥）

DES对称加密技术

DES(Data Encryption Standard)算法，于1977年得到美国政府的正式许可，是一种用56位密钥来加密64位数据的方法。美国国家标准局1973年开始研究除国防部外的其它部门的计算机系统的数据加密标准，于1973年5月15日和1974年8月27日先后两次向公众发出了征求加密算法的公告，提出了四点具体的要求：

提供高质量的数据保护，防止数据未经授权的泄露和未被察觉的修改
具有相当高的复杂性，使得破译的开销超过可能获得的利益，同时又要便于理解和掌握
DES密码体制的安全性应该不依赖于算法的保密，其安全性仅以加密密钥的保密为基础
实现经济，运行有效，并且适用于多种完全不同的应用

DES算法的安全性

DES算法正式公开发表以后，引起了一场激烈的争论。1977年Diffie和Hellman提出了制造一个每秒能测试106个密钥的大规模芯片，这种芯片的机器大约一天就可以搜索DES算法的整个密钥空间，制造这样的机器需要两千万美元。

1993年R.Session和M.Wiener给出了一个非常详细的密钥搜索机器的设计方案，它基于并行的密钥搜索芯片，此芯片每秒测试5×107个密钥，当时这种芯片的造价是10.5美元，5760个这样的芯片组成的系统需要10万美元，这一系统平均1.5天即可找到密钥，如果利用10个这样的系统，费用是100万美元，但搜索时间可以降到2.5小时。可见这种机制是不安全的。

1997年1月28日，美国的RSA数据安全公司在互联网上开展了一项名为“密钥挑战”的竞赛，悬赏一万美元，破解一段用56比特密钥加密的DES密文。

计划公布后引起了网络用户的强力响应。一位名叫Rocke Verser的程序员设计了一个可以通过互联网分段运行的密钥穷举搜索程序，组织实施了一个称为DESHALL的搜索行动，成千上万的志愿者加入到计划中。

在计划实施的第96天，即挑战赛计划公布的第140天，1997年6月17日晚上10点39分，美国盐湖城Inetz公司的职员Michael Sanders成功地找到了密钥，在计算机上显示了明文：“The unknown message is: Strong cryptography makes the world a safer place”。

由此可见，DES的56位短密钥面临着Internet超级计算能力的挑战。 Internet仅仅应用了闲散的资源，就可以破解DES的密码，这是对密码方法的挑战，也是Internet超级计算能力的显示。尽管DES存在着不足，但是作为第一个公开密码算法的密码体制，它成功的完成了自己的使命，在密码学历史上具有重要的地位。

DES算法的原理

DES算法的入口参数有三个：Key、Data、Mode。其中Key为8个字节共64位，是DES算法的工作密钥；Data也为8个字节64位，是要被加密或被解密的数据；Mode为DES的工作方式有两种：加密或解密

DES算法的工作方式：如Mode为加密，则用Key去把数据Data进行加密，生成Data的密码形式（64位）作为DES的输出结果；如Mode为解密，则用Key去把密码形式的数据Data解密，还原为Data的明码形式（64位）作为DES的输出结果

在通信网络的两端，双方约定一致的Key 在通信的源点用Key进行DES加密，以密文的形式在公共通信网中传输密文，在通信的接收端用Key进行DES解密，这样就保证了核心数据（例如PIN，MAC等）在公共通信网中传输的安全性可靠性定期更换Key，能进一步提高数据保密性，这是目前金融交易网络的流行做法

DES算法的实现步骤

第一步：变换明文。对给定的64位的明文x，首先通过一个置换IP表来重新排列x，从而构造出64位比特的x0，x0=IP(x)=L0R0，其中L0表示x0的前32位，R0表示x0的后32位。

第二步：按照规则迭代，规则为：

第三步：对L16R16利用IP-1作逆置换，就得到了密文y，加密过程如图所示：

从图中可以看出，DES加密需要四个关键点：

IP置换表和IP-1逆置换表
函数f
子密钥Ki
S盒的工作原理

IP置换表和IP-1逆置换表

输入的64位数据按置换IP表进行重新组合，并把输出分为L0、R0两部分，每部分各长32位，其置换IP表如表所示

将输入64位比特的第58位换到第一位，第50位换到第二位，依此类推，最后一位是原来的第7位。L0、R0则是换位输出后的两部分，L0是输出的左32位，R0是右32位。比如：置换前的输入值为D1D2D3…D64，则经过初始置换后的结果为：L0=D58D50...D8，R0=D57D49...D7

经过16次迭代运算后。得到L16、R16，将此作为输入，进行逆置换，即得到密文输出。逆置换正好是初始置的逆运算，例如，第1位经过初始置换后，处于第40位，而通过逆置换IP-1，又将第40位换回到第1位，其逆置换IP-1规则表所示

函数f

函数f有两个输入：32位的Ri-1和48位Ki，f函数的处理流程如图所示

E变换的算法是从Ri-1的32位中选取某些位，构成48位。即E将32比特扩展变换为48位，变换规则根据E位选择表，如表所示

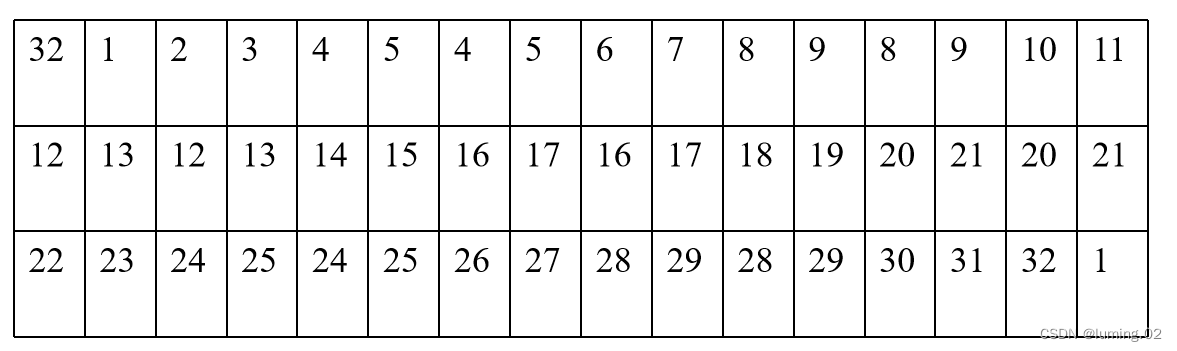
Ki是由密钥产生的48位比特串，具体的算法下面介绍。将E的选位结果与Ki作异或操作，得到一个48位输出。分成8组，每组6位，作为8个S盒的输入

每个S盒输出4位，共32位，S盒的工作原理将在第四步介绍。S盒的输出作为P变换的输入，P的功能是对输入进行置换，P换位表如表所示

子密钥ki

假设密钥为K，长度为64位，但是其中第8、16、24、32、40、48、64用作奇偶校验位，实际上密钥长度为56位。K的下标i的取值范围是1到16，用16轮来构造。构造过程如图所示

首先，对于给定的密钥K，应用PC1变换进行选位，选定后的结果是56位，设其前28位为C0，后28位为D0。PC1选位如表所示

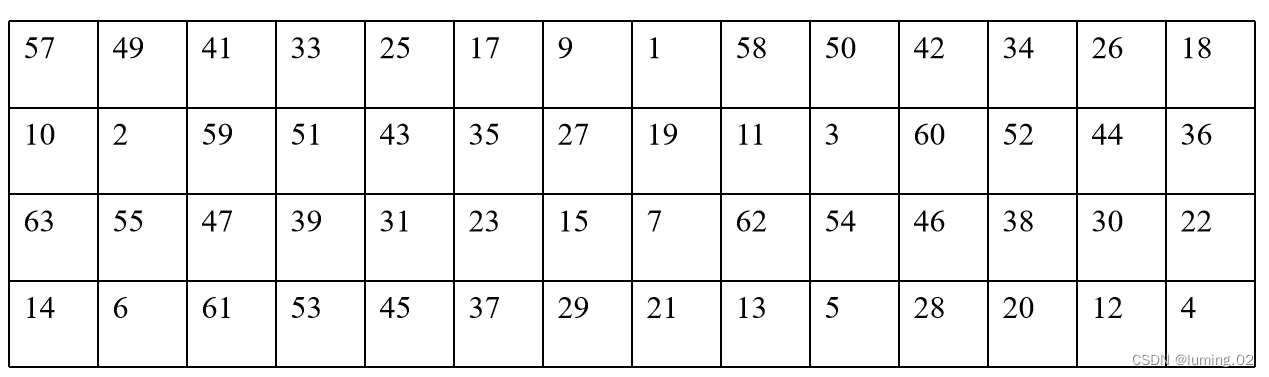
第一轮：对C0作左移LS1得到C1，对D0作左移LS1得到D1，对C1D1应用PC2进行选位，得到K1。其中LS1是左移的位数，如表所示

表中的第一列是LS1，第二列是LS2，以此类推。左移的原理是所有二进位向左移动，原来最右边的比特位移动到最左边。其中PC2如表9-7所示。(56位转换为48位，该48位二进制字符串即为K1)

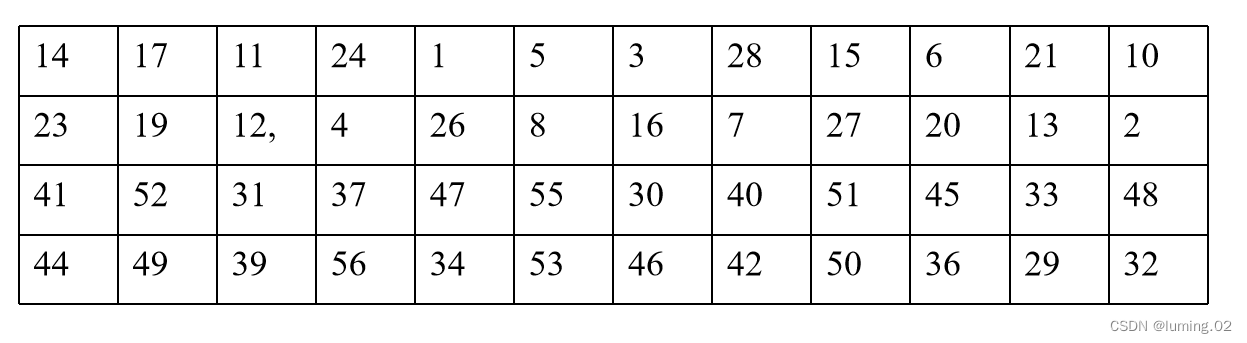
第二轮：对C1，D1作左移LS2得到C2和D2，进一步对C2D2应用PC2进行选位，得到K2。如此继续，分别得到K3，K4…K16

S盒的工作原理

S盒以6位作为输入，而以4位作为输出，现在以S1为例说明其过程。假设输入为A=a1a2a3a4a5a6，则a2a3a4a5所代表的数是0到15之间的一个数，记为：k=a2a3a4a5；由a1a6所代表的数是0到3间的一个数，记为h= a1a6

在S盒中的S1的h行，k列找到一个数B，B在0到15之间，它可以用4位二进制表示，为B=b1b2b3b4，这就是S1的输出。

DES算法的应用误区

DES算法具有比较高安全性，到目前为止，除了用穷举搜索法对DES算法进行攻击外，还没有发现更有效的办法。 56位长的密钥的穷举空间为256，这意味着如果一台计算机的速度是每一秒种检测一百万个密钥，则它搜索完全部密钥就需要将近2285年的时间，可见，这是难以实现的，当然，随着科学技术的发展，当出现超高速计算机后，我们可考虑把DES密钥的长度再增长一些，以此来达到更高的保密程度。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/AllinToyou/article/detail/411764