【PyTorch实战】生成对抗网络GAN：生成动漫人物头像_使用生成对抗网络进行动漫图像生成

Generative Adversarial Networks, 简称GAN，是一个训练生成模型的新框架。其变种有： WGAN、 InfoGAN、 f-GANs、 BiGAN、 DCGAN、 IRGAN等。

回顾：生成模型和判别模型

首先简要介绍一下生成模型（Generative model）与判别模型（Discriminative mode）的概念：

• 生成模型：对联合概率进行建模，从统计的角度表示数据的分布情况，刻画数据是如何生成的，收敛速度快，例如朴素贝叶斯，GDA，HMM等。
• 判别模型：对条件概率$P(Y|X)$进行建模，不关心数据如何生成，主要是寻找不同类别之间的最优分类面，例如LR，SVM等。

判别模型在深度学习乃至机器学习领域取得了巨大成功，其本质是将样本的特征向量映射成对应的label；而生成模型由于需要大量的先验知识去对真实世界进行建模，且先验分布的选择直接影响模型的性能，因此此前人们更多关注于判别模型方法。生成式对抗网络（Generative Adversarial Networks，GANs）是蒙特利尔大学的Goodfellow Ian于2014年提出的一种生成模型， 在之后引起了业内人士的广泛关注与研究。

1. GANs的基本思想和训练过程

GANs的主要框架包括两个部分：生成器（Generator）和判别器（Discriminator）两个部分。生成器用来合成“假”样本，判别器用来判断输入的样本是真实的还是合成的。
具体来说： 生成器从先验分布中采得随机信号，经过神经网络的变换，得到模拟样本；判别器既接受来自生成器的模拟样本，也接收来自实际数据集的真实样本，但是并不告诉判别器样本来源，需要它自己判断。

总之，生成器要尽可能造出样本迷惑判别器，而判别器则尽可能识别出来自生成器的样本。理想情况下，生成器和判别器最终达到一种平衡，双方都臻于完美，彼此都没有更进一步的空间。

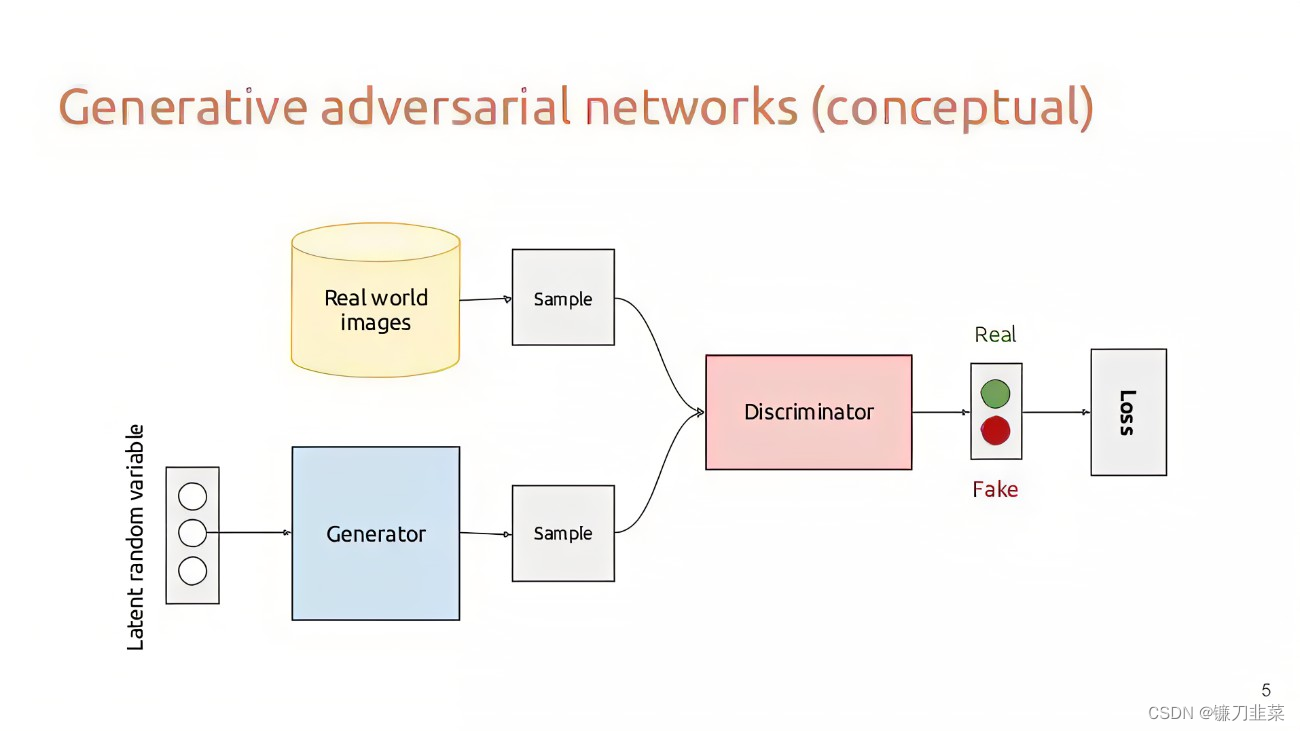
GANs采用对抗策略进行模型训练。具体训练时，采用生成器和判别器交替优化的方式。

TensorFlow实现中，生成模型与判别模型的参数分别定义为params_gen, params_dis，在选择优化器的同时，指定需要优化参数是params_gen还是params_dis即可训练模型是生成模型或者判别模型。
1

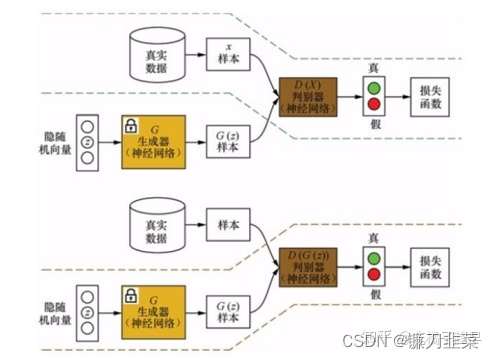
（1）在训练判别器时，先固定生成器$G(\cdot )$；然后利用生成器随机模拟产生样本$G(z)$作为负样本（z是一个随机变量），并从真实数据集中采样获得正样本$X$；将这些正负样本输入到判别器$D(\cdot )$中，根据判别器的输出（即$D(X)$或者$D(G(z))$）和样本标签来计算误差；最后利用误差反向传播算法来更新判别器$D(\cdot )$的参数。判别器的训练过程如下图所示：

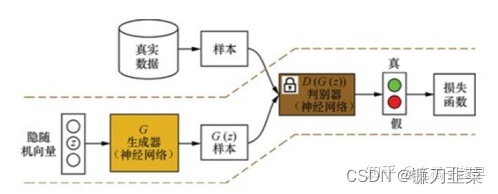
（2）在训练生成器时，先固定判别器$D(\cdot )$；然后利用当前生成器$G(\cdot )$随机模拟产生样本$G(z)$，并输入到判别器$D(\cdot )$中；根据判别器的输出$D(G(z))$和样本标签来计算误差，最后利用误差反向传播算法来更新生成器$G(\cdot )$的参数，如下图所示：

2. GANs的值函数

GANs是一个双人MiniMax游戏。理想情况下游戏最终会达到一个纳什均衡点，此时记生成器为$G\ast$，判别器为$D\ast$，回答如下问题：

1. 此时的解$(G\ast ,D\ast )$，以及对应的值函数的取值。
2. 在未达到均衡点时，将生成器G固定，寻找当下最优的判别器$D_G^{\ast }$，请给出$D_G^{\ast }$和此时的值函数。
3. 进一步地，倘若固定D而将G优化到底，那么解$G_D^{\ast }$和此时的值函数是什么？

因为判别器D试图识别实际数据为真实样本，识别生成器生成的数据为模拟样本，所以这是一个二分类问题，损失函数为Negative Log-Likelihood，也称为Categorical Cross-Entropy Loss，即:
[1]
$$\mathcal{L}(\mathcal{D})=-\int p(x)[p(data|x)\log D(x)+p(g|x)\log (1-D(x))]dx$$
其中，$D(x)$表示判别器预测x为真实样本的概率，$p(data|x)$和$p(g|x)$表示x分属真实数据集和生成器这两类的的概率。样本x的来源一半是实际数据集，一半是生成器，$p_{src}(data)=p_{src}(g)=0.5$。

用$p_{data}(x)\doteq p(x|data)$表示从实际数据集得到x的概率，$p_g(x)=\doteq p(x|g)$表示从生成器得到x的概率，有x的总概率：
[2]
$$p(x)=p_{src}(data)p(x|data)+p_{src}(g)p(x|g)$$
替换[1]中的$p(x)p(data|x)$为$p_{src}(data)p_{d}ata(x)$，以及$p(x)p(g|x)$为$p_{src}(g)p_g(x)$，即可得到最终的目标函数：
[3]
$$\mathcal{L}(D)=-\frac{1}{2}({\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x)]+{\mathbb{E}}_{x\sim p_g(x)}[\log (1-D(x))])$$
在此基础上得到值函数：
[4]
$$V(G,D)={\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x)]+{\mathbb{E}}_{x\sim p_g(x)}[\log (1-D(x))]$$
判别器D最大化上述值函数，生成器G则最小化它，整个MiniMax游戏可表示为: ${\min }_G{\max }_{D}V(G,D)$。

训练中，给定生成器G，寻找当下最优判别器$D_G^{\ast }$。对于单个样本x，最大化${\max }_D{p}_{data}(x)\log D(x)+p_g(x)\log (1-D(x))$的解为$\hat{D}(x)=p_{data}(x)/[p_{data}(x)+p_g(x)]$， 外面套上对x的积分就得到${\max }_{D}V(G,D)$，解由单点变成一个函数解：
[5]
$$D_G^{\ast }=\frac{p_{data}}{p_{data}+p_g}$$
此时， min ⁡ G V ( G , D G ∗ ) = min ⁡ G { − l o g 4 + 2 ⋅ J S D ( p d a t a ∣ ∣ p g ) } \min_G {V(G, D_G^*)}=\min_G \{-log 4+2 \cdot JSD(p_{data}||p_g)\} minG​V(G,DG∗​)=minG​{−log4+2⋅JSD(pdata​∣∣pg​)}，其中$JSD(\cdot )$是JS距离（Jensen-Shannon Divergence）。

- KL散度：用来衡量两个分布之间的差异，等于一个交叉熵减去一个信息熵（交叉熵损失函数的由来），具有两个性质：非负性（用Jenson‘s inequality 证明）
不对称性。
- JS(Jenson’s Shannon)散度：一般地，JS散度是对称的，其取值是0到1之间。如果两个分布P,Q离得很远，完全没有重叠的时候，那么KL散度值是没有意义的，而JS散度值是一个常数。这就意味这这一点的梯度为 0。梯度消失了。

JS散度的缺陷：当两个分布完全不重叠时，即便两个分布的中心距离有多近，其JS散度是一个常数，以至于梯度为0，无法更新。

为什么会出现两个分布没有重叠的现象？从理论和经验上来说，真实的数据分布通常是一个低维流形，简单地说就是数据不具备高维特性，而是存在一个嵌入在高维度的低维空间内。
1
2
3
4
5
6
7

由此看出，优化生成器G实际是在最小化生成样本分布与真实样本分布之间的JS距离。最终，达到均衡点是$JSD(p_{data}||p_g)$的最小值点，即$p_g=p_{data}$时，$JSD(p_{data}||p_g)$取到零，最优解$G^{\ast }(z)=x\sim p_{data}(x),D^{\ast }(x)\equiv \frac{1}{2}$，值函数$V(G\ast ,D\ast )=-\log 4$。

进一步地，训练时如果给定D求解最优G，可以得到什么？假设$G^{\prime }$表示前一步的生成器，D是$G^{\prime }$下的最优判别器$D_G^{\ast }$。那么求解最优G的过程为：
[6]
$$\arg \underset{G}{\min }V(G,D_G^{\ast })=\arg \underset{G}{\min }KL(p_g||\frac{p_{data}+p_{g^{\prime }}}{2})-KL(p_g||p_{g^{\prime }})$$
由此，可以得出以下两个结论：
（1）优化G的过程是让G远离前一步的$G^{\prime }$，同时接近分布$\frac{p_{data}+p_{g^{\prime }}}{2}$。
（2）达到均衡点时$p_{g^{\prime }}=p_{data}$，有$\arg {\min }_{G}V(G,D_G^{\ast })=\arg {\min }_{G}0$，如果用这时的判别器去训练一个全新的生成器$G_{new}$，理论上可能啥也训练不出来。

3. GANs如何避开大量概率推断计算？

传统概率生成模型方法，如马尔科夫随机场、贝叶斯网络等，会涉及大量难以完成的概率推断计算，GANs是如何避开这类计算的？

传统概率生成模型要定义一个概率分布表达式$P(X)$，通常是一个多变量联合概率分布的密度函数$p(X_1,X_2,...,X_N)$，并基于此做最大似然估计。这个过程中少不了概率推断计算，比如计算边缘概率$P(X_i)$、条件概率$P(X_i|X_j)$以及作分母的Partition Function等。当随机变量很多时，概率模型会变得十分复杂。

GANs在刻画概率生成模型时，并不对概率密度函数$p(X)$直接建模，而是通过制造样本x，间接体现出分布$p(X)$。具体地：
如果随机变量Z和X之间满足某种映射关系$X=f(Z)$，那么它们的概率分布$p_X(X)$和$p_Z(Z)$也存在某种映射关系。当$Z,X\in \mathbb{R}$都是一维随机变量时，$p_X=\frac{df(Z)}{dX}{p}_Z$；当$Z,X$是高维随机变量时，导数变成雅可比矩阵，即$p_X=J{p}_Z$。因此，已知Z的分布，对随机变量间的转换函数$f$直接建模，就唯一确定了$X$的分布。

这样，避开了大量复杂的概率计算，而且给$f$更大的发挥空间，可以用神经网络来训练$f$。除了经典的卷积神经网络和循环神经网络，还有ReLU激活函数、批量归一化、Dropout等，都可以自由地添加到生成器的网络中，大大增强生成器的表达能力。

4. GANs在实际训练中会遇到什么问题？

最小化目标函数${\mathbb{E}}_{z\sim p(z)}[\log (1-D(G(z;{\theta }_g)))]$求解G会遇到什么问题？如何解决。

在实际训练中，早期阶段生成器G很差，生成的模拟样本很容易被判别器D识别，使得D回传给G的梯度极其小，达不到训练目的，这个现象称为优化饱和。

为什么会这样呢？将D的Sigmoid输出层的前一层记为$o$，那么$D(x)$可表示成$D(x)=Sigmoid(o(x))$，此时有
[7]
$$\nabla D(x)=\nabla Sigmoid(o(x))=D(x)(1-D(x))\nabla o(x)$$
，因此训练G的梯度为：
[8]
$$\nabla \log (1-D(G(z;{\theta }_g)))=-D(G(z;{\theta }_g))\nabla o(G(z;{\theta }_g))$$
当D很容易认出模拟样本时，意味着认错模拟样本的概率几乎为零，即$D(G(z;{\theta }_g))\to 0$。假定$|\nabla o(G(z;{\theta }_g))|<C$，C是一个常量，则可推出：
[9]
$$\underset{D(G(z;{\theta }_g))\to 0}{\lim }\nabla \log (1-D(G(z;{\theta }_g)))=-\underset{D(G(z;{\theta }_g))\to 0}{\lim }D(G(z;{\theta }_g))\nabla o(G(z;{\theta }_g))=0$$
故G获得的梯度基本为零，这说明D强大后对G的帮助反而微乎其微。

解决方法是将$\log (1-D(G(z;{\theta }_g)))$变为$\log (D(G(z;{\theta }_g)))$，形式上有一个负号的差别，故让后者最大等效于让前者最小，二者在最优时解相同。
更改后的目标函数的梯度是：
[10]
$$\nabla \log (D(G(z;{\theta }_g)))=(1-D(G(z;{\theta }_g)))\nabla o(G(z;{\theta }_g))$$
[11]
$$\underset{D(G(z;{\theta }_g))\to 0}{\lim }\nabla \log (D(G(z;{\theta }_g)))=\nabla o(G(z;{\theta }_g))$$
，即使$D(G(z;{\theta }_g))$趋于零，$\nabla \log (D(G(z;{\theta }_g)))$也不会消失，仍能给生成器提供有效的梯度。

5. 用GAN生成动漫人物的头像

GAN解决了非监督学习问题中的著名问题：给定一批样本，训练一个系统能够生成类似的新样本。在本案例中，主要包含两个子网络：

• 生成器（generator）：输入一个随机噪声，生成一张图片。
• 判别器（discriminator）：判断输入的图片是真图片还是假图片。

这里我们采用广泛使用的DCGAN（Deep Convolutional Generative Adversarial Networks）结构，即采用全卷积网络，其结构如下图所示。

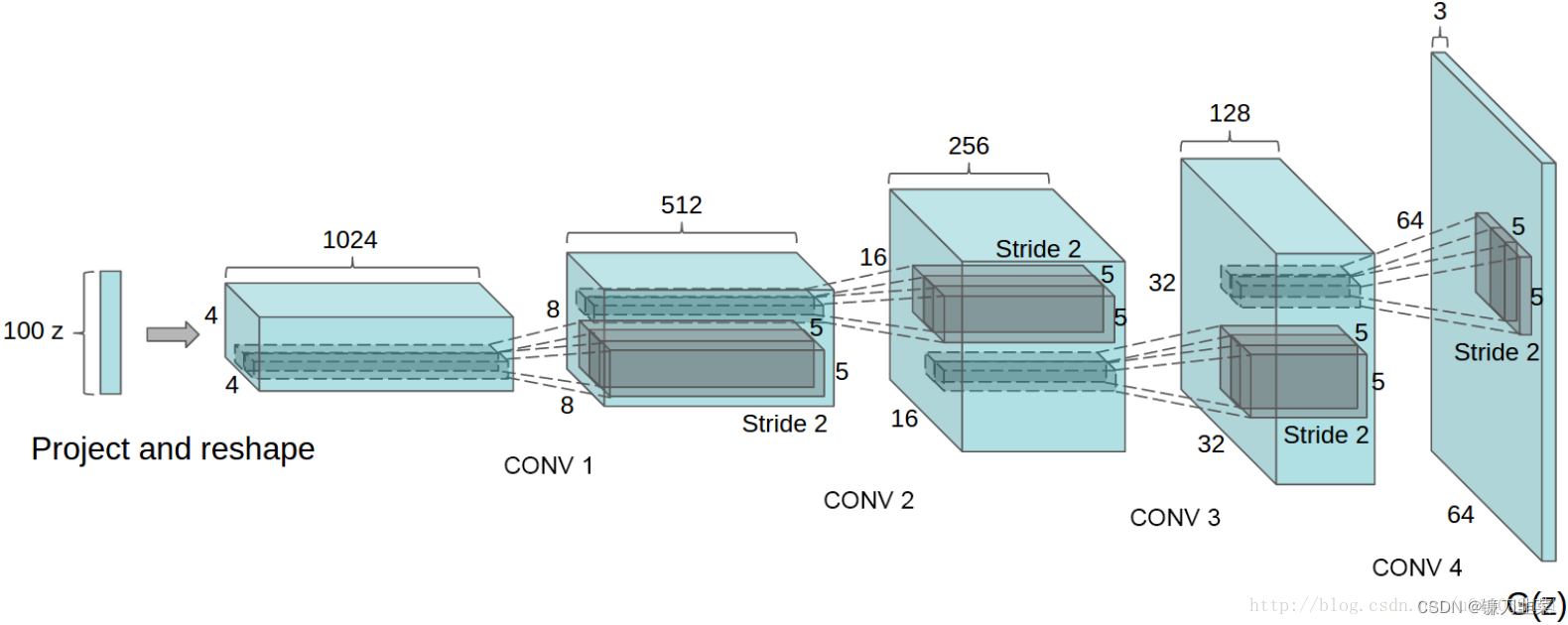
网络的输入是一个100维的噪声，输出是一个3×64×64的图片。这里的输入可以看成是一个100×1×1的图片，通过上卷积慢慢增大为4×4、8×8、16×16、32×32和64×64。

上卷积，或称为转置卷积，是一种特殊的卷积操作，类似于卷积操作的逆运算。
当卷积的stride为2时，输出相比输入会下采样到一半的尺寸；而当上卷积的stride为2时，输出会上采样到输入的两倍尺寸。
1
2

这种上采样的做法可以理解为图片的信息保存于100个向量之中，神经网络根据这100个向量描述的信息，前几步的上采样先勾勒出轮廓、色调等基础信息，后几步上采样则慢慢完善细节。网络越深，细节越详细。

DCGANs的基本架构就是使用几层“反卷积”（Deconvolution）。传统的CNN是将图像的尺寸压缩，变得越来越小，而反卷积是将初始输入的小数据（噪声）变得越来越大（但反卷积并不是CNN的逆向操作），例如在上面这张图中，从输入层的100维noise，到最后输出层64x64x3的图片，从小维度产生出大的维度。反卷积的示意图如下所示，2x2的输入图片，经过3x3 的卷积核，可产生4x4的feature map：

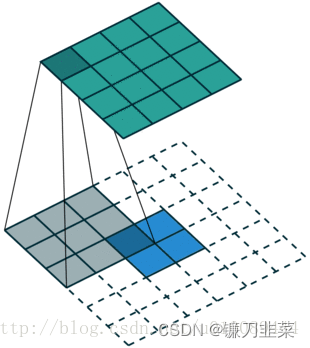
由于反卷积存在于卷积的反向传播中。其中反向传播的卷积核矩阵是前向传播的转置，所以其又可称为transport convolution。只不过我们把反向传播的操作拿到了前向传播来做，就产生了所谓的反卷积一说。但是transport convolution只能还原信号的大小，不能还原其值，因此不是真正的逆操作。

DCGAN的另一个改进是对生成模型中池化层的处理，传统CNN使用池化层（max-pooling或mean-pooling）来压缩数据的尺寸。在反卷积过程中，数据的尺寸会变得越来越大，而max-pooling的过程并不可逆，所以DCGAN的论文里并没有采用池化的逆向操作，而只是让反卷积的滑动步长设定为2或更大值，从而让尺寸按我们的需求增大。另外，DCGAN模型在核上均使用了batch normalization，这使得训练过程更加稳定和可控。

文献[3]将GANs应用于文本转图像（Text to Image），从而可根据特定输入文本所描述的内容来产生特定图像。因此，生成模型里除了输入随机噪声之外，还有一些特定的自然语言信息。所以判别模型不仅要区分样本是否是真实的，还要判定其是否与输入的语句信息相符。网络结构如下图所示：

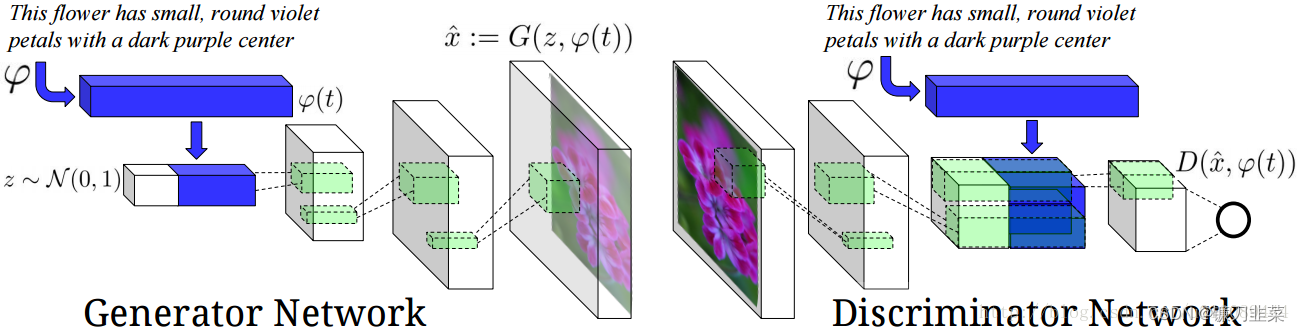
在本案例中, DCGAN中，判别器的结构和生成器对称：生成器中采用上采样的卷积，判别器中就采用下采样的卷积，生成器是根据噪声输出一张６４×６４×３的图片，而判别器则是根据输入的６４×６４×３的图片输出图片属于正负样本的分数（概率）。

在生成图像中，我们需要不断的扩大图像的尺寸。ConvTranspose2d是其中一个方法。DCGAN论文中，可以称为fractionally-strided convolutions， 也有的称为deconvolutions, 但实际上并不是. 为了简化说明，暂且称为"逆卷积".
首先, 理解什么是卷积。对于一个图片A，设定它的高度和宽度分别为Height，Width，通道数为Channels。 然后用卷积核（kernel * kernel）去做卷积（这里假定卷积核为正方形，长方形卷积核类似），步长为stride(同样的，不区分高宽方向)，做填充padding。卷积后得到图片B。也就是说, 就是利用一个卷积操作将A变成B。

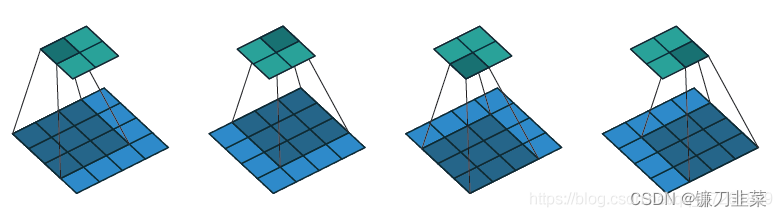
然后,理解什么是逆卷积。如下图所示：

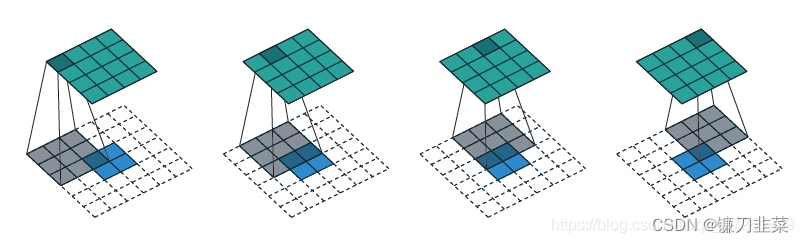
逆卷积操作的输入就是特征图y, 卷积核设置同上。要得到上面的特征图x。
那么, 怎么求逆卷积ConvTranspose2d（fractionally-strided convolutions）？

nn.ConvTranspose2d(): 在由多个输入平面组成的输入图像上应用二维转置卷积运算符。
参数：
- in_channels（int）–输入图像中的通道数
- out_channels（int）–卷积产生的通道数
- kernel_size（int或元组）–卷积内核的大小
- stride（int或tuple，可选）–卷积的步幅。默认值：1
- padding（int或tuple，可选）– 零填充将添加到输入中每个维度的两侧。默认值：0 dilation * (kernel_size - 1) - padding
- output_padding（int或tuple，可选）–在输出形状的每个尺寸的一侧添加的附加大小。默认值：0
- groups（int，可选）–从输入通道到输出通道的阻塞连接数。默认值：1
- bias（bool，可选）–如果为True，则向输出添加可学习的偏见。默认：True
- dilation（int或tuple，可选）–内核元素之间的间距。默认值：1
1
2
3
4
5
6
7
8
9
10
11

• Input: $(N,C_{in},H_{in},W_{in})$
• Output: $(N,C_{out},H_{out},W_{out})$
• $H_{out}=(H_{in}-1)\times stride[0]-2\times padding[0]+dilation[0]\times (kerne{l}_{s}ize[0]-1)+outpu{t}_{p}adding[0]+1$
• $W_{out}=(W_{in}-1)\times stride[1]-2\times padding[1]+dilation[1]\times (kerne{l}_{s}ize[1]-1)+outpu{t}_{p}adding[1]+1$

---

首先看生成器和判别器的代码：

# -*- coding: utf-8 -*-#

# ----------------------------------------------
# Name:         model.py
# Description:
# Author:       PANG
# Date:         2022/6/23
# ----------------------------------------------

# Generator Code

class Generator(nn.Module):
    def __init__(self, ngpu):
        super(Generator, self).__init__()
        self.ngpu = ngpu
        self.main = nn.Sequential(
            # input is Z, going into a convolution
            nn.ConvTranspose2d( nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # state size. (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # state size. (ngf*4) x 8 x 8
            nn.ConvTranspose2d( ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # state size. (ngf*2) x 16 x 16
            nn.ConvTranspose2d( ngf * 2, ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # state size. (ngf) x 32 x 32
            nn.ConvTranspose2d( ngf, nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # state size. (nc) x 64 x 64
        )

    def forward(self, input):
        return self.main(input)

# Create the generator
netG = Generator(ngpu).to(device)

# Handle multi-gpu if desired
if (device.type == 'cuda') and (ngpu > 1):
    netG = nn.DataParallel(netG, list(range(ngpu)))

# Apply the weights_init function to randomly initialize all weights
#  to mean=0, stdev=0.02.
netG.apply(weights_init)

# Print the model
print(netG)

class Discriminator(nn.Module):
    def __init__(self, ngpu):
        super(Discriminator, self).__init__()
        self.ngpu = ngpu
        self.main = nn.Sequential(
            # input is (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        return self.main(input)

# Create the Discriminator
netD = Discriminator(ngpu).to(device)

# Handle multi-gpu if desired
if (device.type == 'cuda') and (ngpu > 1):
    netD = nn.DataParallel(netD, list(range(ngpu)))

# Apply the weights_init function to randomly initialize all weights
#  to mean=0, stdev=0.2.
netD.apply(weights_init)

# Print the model
print(netD)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96

生成器的搭建相对比较简单，直接使用nn.Sequential将上卷积、激活、池化等操作拼接起来即可，需要注意的是上卷积ConvTranspose2d的使用。 当kernel size为4， stride为2， padding为1时，根据公式$H_{out}=(H_{in}-1)\ast stride-2\ast padding+kerne{l}_{s}ize$，输出尺寸刚好变成输入的两倍。最后一层使用Tanh将输出图片的像素归一化至$-11$，如果希望归一化至$01$，则需使用Sigmoid。

判别器的网络结构几乎和生成器对称。注意生成器的激活函数用的是ReLU，而判别器使用的是LeakyReLU。二者并无本质区别，更多是经验总结。

---

损失函数和优化器

# Initialize BCELoss function
criterion = nn.BCELoss()

# Create batch of latent vectors that we will use to visualize
#  the progression of the generator
fixed_noise = torch.randn(64, nz, 1, 1, device=device)

# Establish convention for real and fake labels during training
real_label = 1.
fake_label = 0.

# Setup Adam optimizers for both G and D
optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=lr, betas=(beta1, 0.999))
1
2
3
4
5
6
7
8
9
10
11
12
13
14

训练过程

# Training Loop

# Lists to keep track of progress
img_list = []
G_losses = []
D_losses = []
iters = 0

print("Starting Training Loop...")
# For each epoch
for epoch in range(num_epochs):
    # For each batch in the dataloader
    for i, data in enumerate(dataloader, 0):

        ############################
        # (1) Update D network: maximize log(D(x)) + log(1 - D(G(z)))
        ###########################
        ## Train with all-real batch
        netD.zero_grad()
        # Format batch
        real_cpu = data[0].to(device)
        b_size = real_cpu.size(0)
        label = torch.full((b_size,), real_label, dtype=torch.float, device=device)
        # Forward pass real batch through D
        output = netD(real_cpu).view(-1)
        # Calculate loss on all-real batch
        errD_real = criterion(output, label)
        # Calculate gradients for D in backward pass
        errD_real.backward()
        D_x = output.mean().item()

        ## Train with all-fake batch
        # Generate batch of latent vectors
        noise = torch.randn(b_size, nz, 1, 1, device=device)
        # Generate fake image batch with G
        fake = netG(noise)
        label.fill_(fake_label)
        # Classify all fake batch with D
        output = netD(fake.detach()).view(-1)
        # Calculate D's loss on the all-fake batch
        errD_fake = criterion(output, label)
        # Calculate the gradients for this batch, accumulated (summed) with previous gradients
        errD_fake.backward()
        D_G_z1 = output.mean().item()
        # Compute error of D as sum over the fake and the real batches
        errD = errD_real + errD_fake
        # Update D
        optimizerD.step()

        ############################
        # (2) Update G network: maximize log(D(G(z)))
        ###########################
        netG.zero_grad()
        label.fill_(real_label)  # fake labels are real for generator cost
        # Since we just updated D, perform another forward pass of all-fake batch through D
        output = netD(fake).view(-1)
        # Calculate G's loss based on this output
        errG = criterion(output, label)
        # Calculate gradients for G
        errG.backward()
        D_G_z2 = output.mean().item()
        # Update G
        optimizerG.step()

        # Output training stats
        if i % 50 == 0:
            print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
                  % (epoch, num_epochs, i, len(dataloader),
                     errD.item(), errG.item(), D_x, D_G_z1, D_G_z2))

        # Save Losses for plotting later
        G_losses.append(errG.item())
        D_losses.append(errD.item())

        # Check how the generator is doing by saving G's output on fixed_noise
        if (iters % 500 == 0) or ((epoch == num_epochs-1) and (i == len(dataloader)-1)):
            with torch.no_grad():
                fake = netG(fixed_noise).detach().cpu()
            img_list.append(vutils.make_grid(fake, padding=2, normalize=True))

        iters += 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

随着GAN研究的逐渐成熟，WGAN、CycleGAN等模型逐渐出现。

参考资料

[1] 理解JS散度(Jensen–Shannon divergence)
[2] GAN：两者分布不重合JS散度为log2的数学证明
[3] Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks[J]. arXiv preprint arXiv:1511.06434, 2015.
[4] 生成式对抗网络（Generative Adversarial Networks，GANs）
[5] ConvTranspose2d原理，深度网络如何进行上采样？
[6] DCGAN TUTORIAL