FPGA：实现快速傅里叶变换（FFT）算法_fpga fft

前言

第一次使用FPGA实现一个算法，搓手手，于是我拿出一股势在必得的心情打开了FFT的视频教程，看了好几个视频和好些篇博客，于是我迷失在数学公式推导中，在一位前辈的建议下，我开始转换我的思维，从科研心态转变为先用起来，于是我关掉我的推导笔记，找了一篇叫我用Verilog写FFT的视频B站 - 使用Verilog写FFT，跟着他先让代码跑起来，然后再择需深入

---

使用软件：vivado
实现算法：N=8的FFT算法
大框架：使用并行的3级流水线

正文

以下内容以快速让FFT代码跑起来为出发点，所以不会有复杂的理论推导，如果想要深入研究，可参考网上的详细教程，以下我会介绍我实现的过程，如果下面内容有误，请一定帮我指出

一、如何用FPGA实现FFT

在这里我们先直接抛出在FPGA里面是如何实现FFT的，然后再逐次推进涉及到的内容

1.1 实现FFT的核心

核心就是用Verilog代码写出下面的这幅图
可能你和我一样一开始不知道 怎么下手，连这个图都看不懂，没关系！！我们一步步来

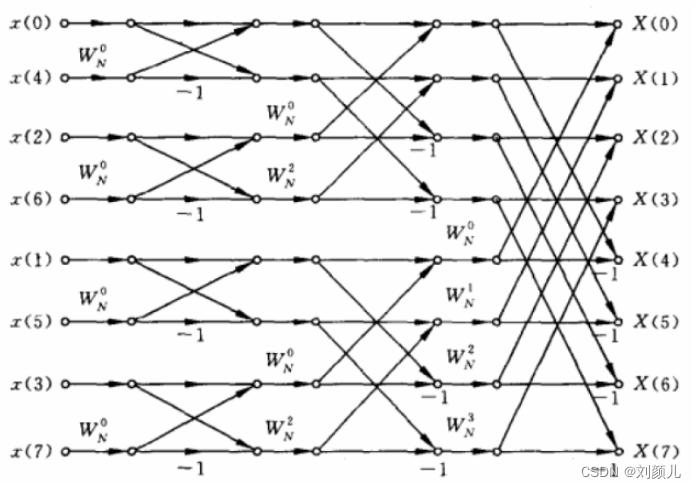
有了目标，就围绕着我们的目标进行知识补充，（这样以目标为导向，不至于迷失在数学公式推导中）
首先我们要知道这个图是个啥，推荐看这个老师的视频，视频时长很短，只需要十多分钟就能对这幅图有个初步的认识
推荐视频：B站-潘老师-数字信号处理

需要明确的地方：

1. 上面的图叫：蝶形图
2. $W_N^0=1$
3. 最左侧是时域，最右侧是 频域

以下是我看了视频后做的笔记：

---

这个口诀可以等你看完视频和我下面的笔记后，用来作为帮助记忆的辅助材料
口诀：
箭尾出发，箭头停
箭身有值要乘上
每次走完2支箭
箭身长的写在前

---

首先最左侧的 $x(0),...,x(7)$ 从箭尾出发，箭身上有值的就和上面的值相乘，每次只能走完2个箭就要停下来计算一次值，并且从斜着的箭过来的值写在计算表达式的第一位，直着过来的值写在计算表达式的第二位
先挖个坑，等有空录一个简单的视频说一说这个蝶形图

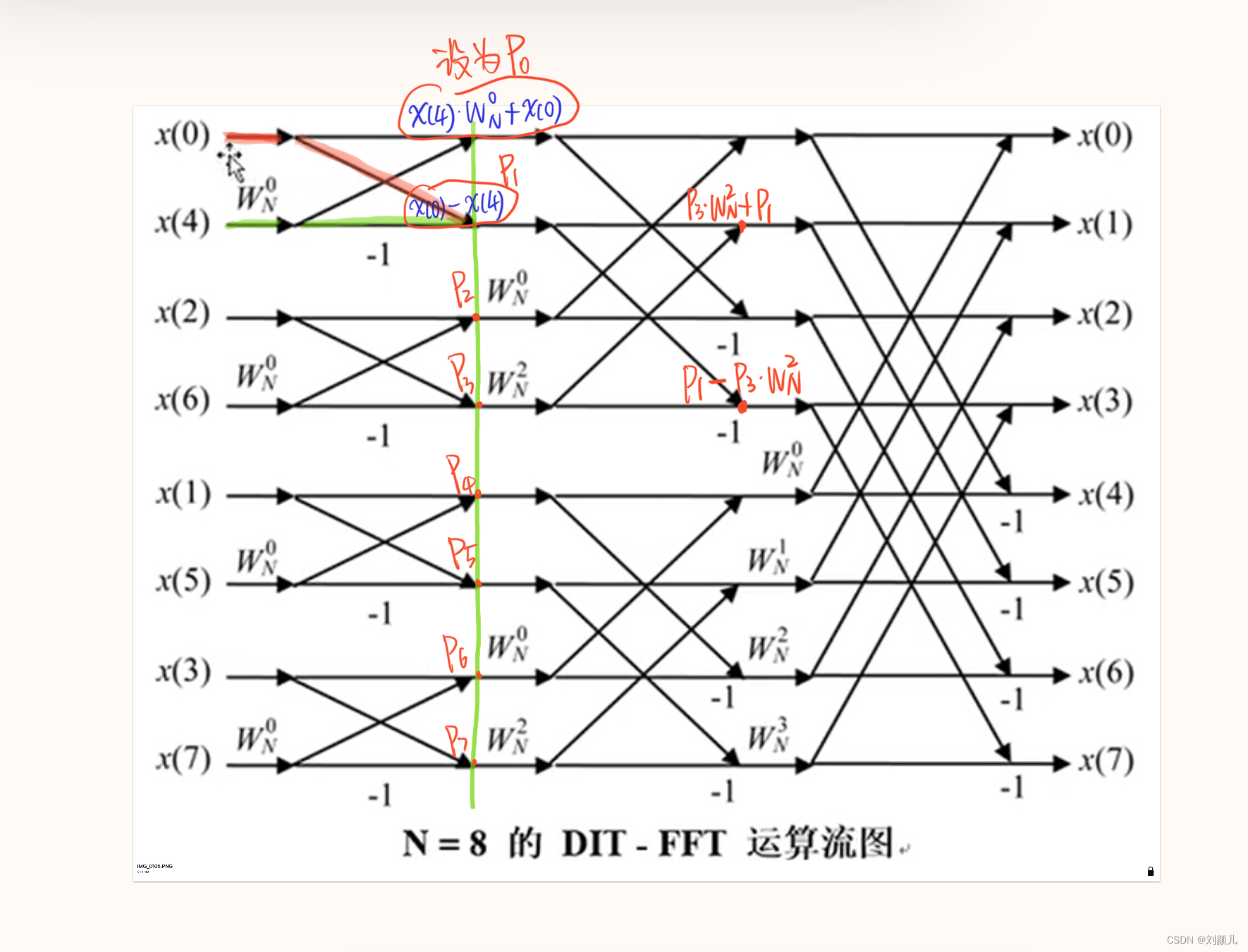
1.2 蝶形图的组成元素

蝶形图无非就是一些元素构成的：左右两边的 $x$ , $W_{N}^{0}$ , $W_{N}^{1}$ , $W_{N}^{2}$ , $W_{N}^{3}$, -1,还有一些箭头，以及图下面图例中 $N=8$
只要我们知道这些元素是啥，用来干什么就能大概看懂蝶形图了

1.2.1 旋转因子 $W_N$

快速傅里叶变换（FFT）是对离散傅里叶变换（DFT）的一种加速算法，FFT比DFT运算速度快的原因，就是这个旋转因子的功劳。
旋转因子的表达式如下：

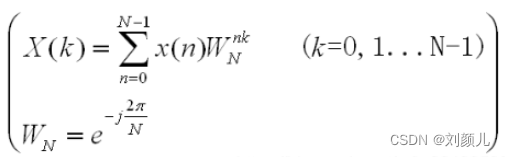
旋转因子有一些比较好的性质：周期性、可约性、对称性，个人认为如果不做公式推导，那就知道它的这些性质即可
在下面的代码中，第二级流水线里的例化复数乘法IP核时，我们直接将旋转因子给出（如下的倒数第三行）

// 复数乘法的IP核，求解与旋转因子的乘积
cmpy_0 cmpy23(
    .aclk(clk),
    .s_axis_a_tvalid(fft1_en),
    .s_axis_a_tdata({4'd0, fft1_im3,1'd0,4'd0, fft1_re3,1'd0}),//乘法元素中的复数：既有实部又有虚部
    .s_axis_b_tvalid(1'b1),
    .s_axis_b_tdata({8'd0,8'b10110101,8'd0,8'b10110101}),// 旋转因子
    .m_axis_dout_tvalid(fft2_en1),
    .m_axis_dout_tdata(fft2_cmpy23)
    );
1
2
3
4
5
6
7
8
9
10

1.2.2 输入数据倒序排列

可能有细心的朋友会发现，蝶形图左边的 $x$ 的排序不是按照升序或降序拍的，而是将 $0-7$ 的二进制写出来后，将二进制的高位、低位互换后得到的

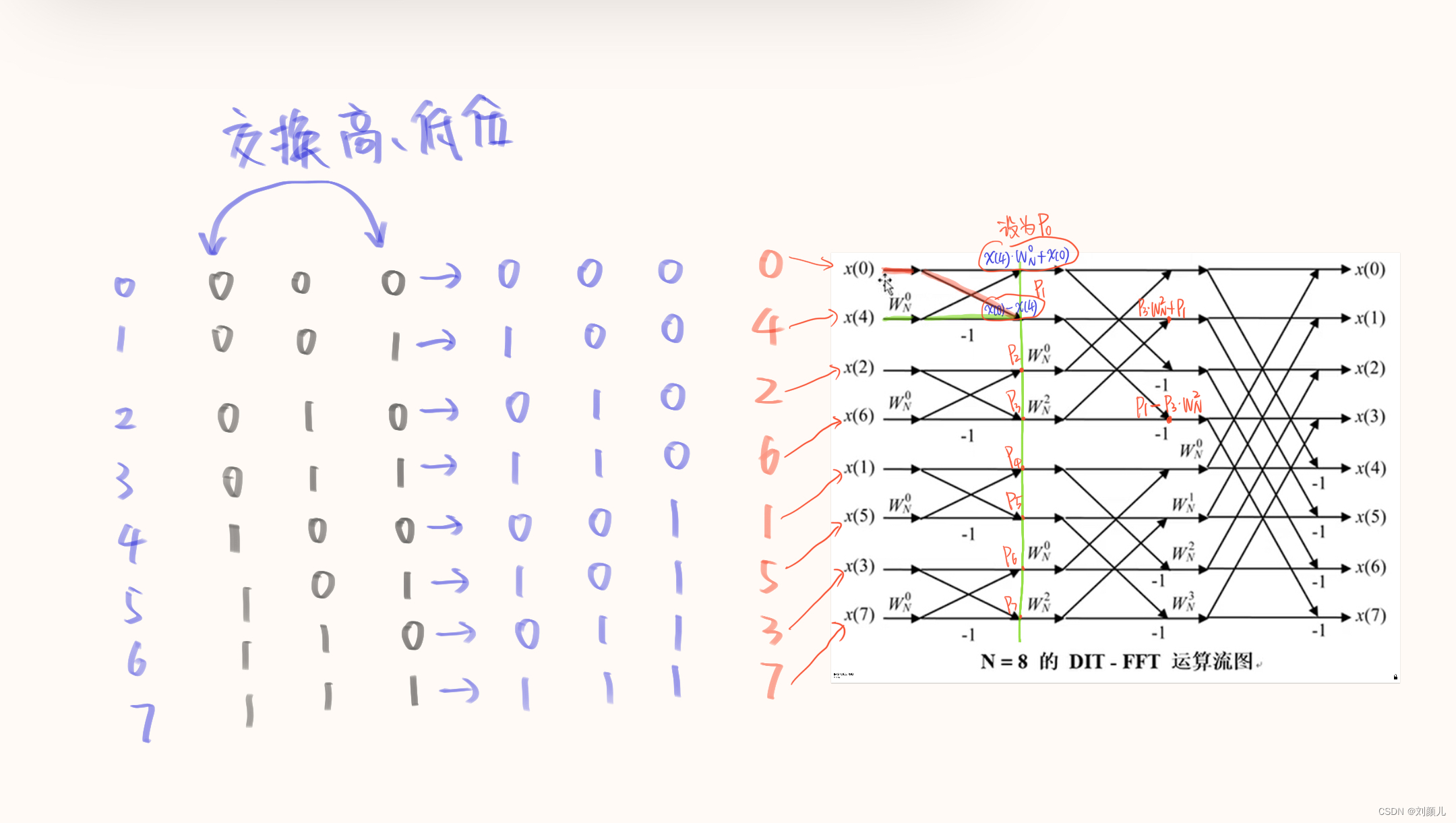
1.2.3 N是什么

目前蝶形图中的元素只剩下这个图例中的 $N=8$ 了，这里的 $N$ 表示每一列的点数，虽然蝶形图中有很多点，但是每一列都只有8个点，$lo{g}_{2}N$= 每组的蝶形次数，这里 $N=8$，每组就要做4次蝶形

我在看教程时，还会看到基-2、基-4这样的名词，$N$ 还可以用来区分这两个名词（虽然我不知道区分这俩有啥用）

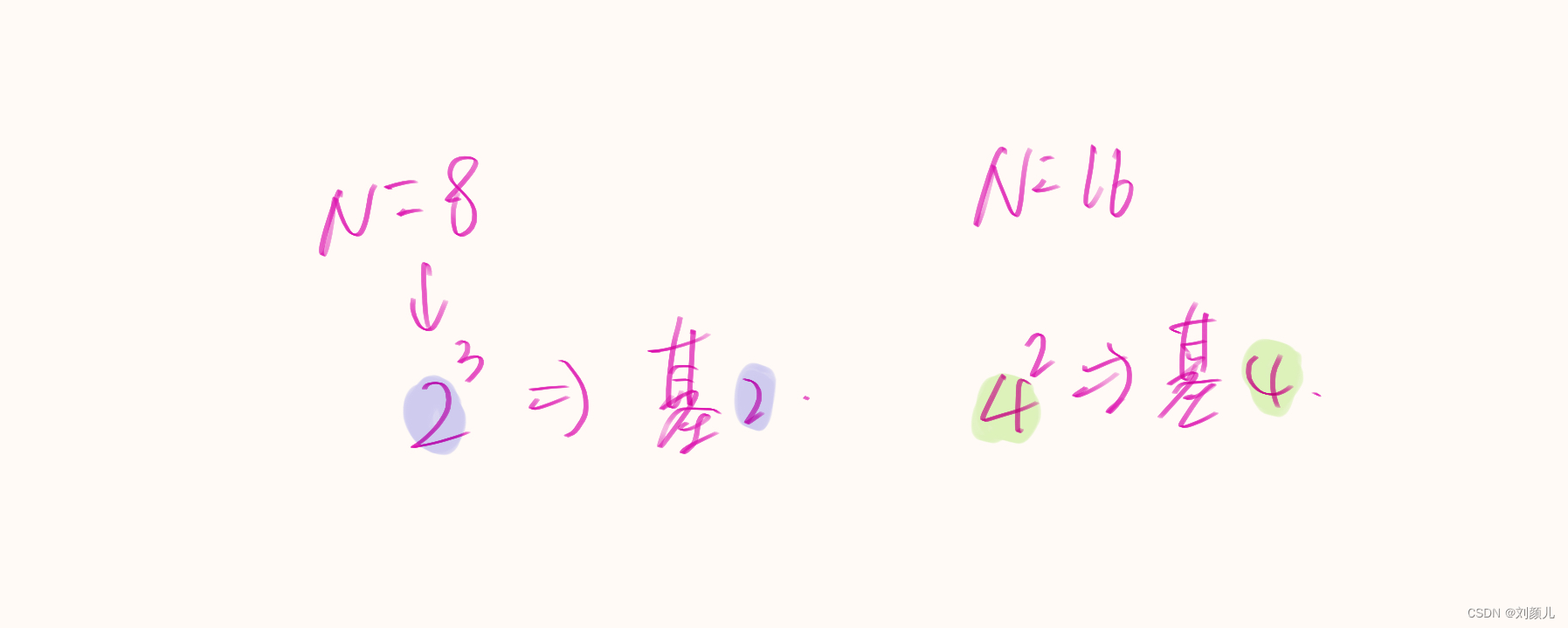
1.3 Verilog编写蝶形图

从图中可以看到，处理N=8这样的蝶形图，分3步走，即可以使用3级流水线来实现

1.3.1 第一级流水线

always @(posedge clk or negedge rst_n)begin
    if(!rst_n)
        begin
            fft1_en  <= 0;
            fft1_re0 <= 0;
            fft1_im0 <= 0;
            fft1_re1 <= 0;
            fft1_im1 <= 0;
            fft1_re2 <= 0;
            fft1_im2 <= 0;
            fft1_re3 <= 0;
            fft1_im3 <= 0;
            fft1_re4 <= 0;
            fft1_im4 <= 0;
            fft1_re5 <= 0;
            fft1_im5 <= 0;
            fft1_re6 <= 0;
            fft1_im6 <= 0;
            fft1_re7 <= 0;
            fft1_im7 <= 0;
        end
    else if(data_in_en)
    begin

    // 实现第一级流水线输出
        fft1_en  <= 1;

        fft1_re0 <= data_in_re0 + data_in_re4;
        fft1_im0 <= data_in_im0 + data_in_im4;
        fft1_re1 <= data_in_re0 - data_in_re4;
        fft1_im1 <= data_in_im0 - data_in_im4;

        fft1_re2 <= data_in_re2 + data_in_re6;
        fft1_im2 <= data_in_im2 + data_in_im6;
        fft1_re3 <= data_in_re2 - data_in_re6;
        fft1_im3 <= data_in_im2 - data_in_im6;

        fft1_re4 <= data_in_re1 + data_in_re5;
        fft1_im4 <= data_in_im1 + data_in_im5;
        fft1_re5 <= data_in_re1 - data_in_re5;
        fft1_im5 <= data_in_im1 - data_in_im5;

        fft1_re6 <= data_in_re3 + data_in_re7;
        fft1_im6 <= data_in_im3 + data_in_im7;
        fft1_re7 <= data_in_re3 - data_in_re7;
        fft1_im7 <= data_in_im3 - data_in_im7;
    end
    else begin
        fft1_en <= 0;       
    end

end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

1.3.2 第二级流水线

// 第二级流水线
wire fft2_en1;
wire signed [10:0] fft2_im3_wn;
wire signed [10:0] fft2_re3_wn;
wire signed [47:0] fft2_cmpy23;

assign fft2_re3_wn = fft2_cmpy23[19:9]; //从48位中提取出实部
assign fft2_im3_wn = fft2_cmpy23[43:33];//从48位中提取出虚部

// 复数乘法的IP核，求解与旋转因子的乘积
cmpy_0 cmpy23(
    .aclk(clk),
    .s_axis_a_tvalid(fft1_en),
    .s_axis_a_tdata({4'd0, fft1_im3,1'd0,4'd0, fft1_re3,1'd0}),//乘法元素中的复数：既有实部又有虚部
    .s_axis_b_tvalid(1'b1),
    .s_axis_b_tdata({8'd0,8'b10110101,8'd0,8'b10110101}),// 旋转因子
    .m_axis_dout_tvalid(fft2_en1),
    .m_axis_dout_tdata(fft2_cmpy23)
    );

wire fft2_en2;
wire signed [10:0] fft2_im7_wn;
wire signed [10:0] fft2_re7_wn;
wire signed [47:0] fft2_cmpy27;
assign fft2_re7_wn =fft2_cmpy27[19:9];
assign fft2_im7_wn =fft2_cmpy27[43:33];

cmpy_0 cmpy27(
    .aclk(clk),
    .s_axis_a_tvalid(fft1_en),
    .s_axis_a_tdata({4'd0, fft1_im7,1'd0,4'd0, fft1_re7,1'd0}),
    .s_axis_b_tvalid(1'b1),
    .s_axis_b_tdata({8'd0,8'b10110101,8'd0,8'b10110101}),
    .m_axis_dout_tvalid(fft2_en2),
    .m_axis_dout_tdata(fft2_cmpy27)
    );

reg fft2_en;
reg signed [11:0] fft2_re0;
reg signed [11:0] fft2_im0;
reg signed [11:0] fft2_re1;
reg signed [11:0] fft2_im1;
reg signed [11:0] fft2_re2;
reg signed [11:0] fft2_im2;
reg signed [11:0] fft2_re3;
reg signed [11:0] fft2_im3;
reg signed [11:0] fft2_re4;
reg signed [11:0] fft2_im4;
reg signed [11:0] fft2_re5;
reg signed [11:0] fft2_im5;
reg signed [11:0] fft2_re6;
reg signed [11:0] fft2_im6;
reg signed [11:0] fft2_re7;
reg signed [11:0] fft2_im7;

always@(posedge clk or negedge rst_n) begin
    if(!rst_n)
    begin
        fft2_en  <= 0;
        fft2_re0 <= 0;
        fft2_im0 <= 0;
        fft2_re1 <= 0;
        fft2_im1 <= 0;
        fft2_re2 <= 0;
        fft2_im2 <= 0;
        fft2_re3 <= 0;
        fft2_im3 <= 0;
        fft2_re4 <= 0;
        fft2_im4 <= 0;
        fft2_re5 <= 0;
        fft2_im5 <= 0;
        fft2_re6 <= 0;
        fft2_im6 <= 0;
        fft2_re7 <= 0;
        fft2_im7 <= 0;
    end
    else if(fft2_en2 && fft2_en1)
        begin

            // 实现第二级流水线输出
            fft2_en  <= 1;

            fft2_re0 <= fft1_re0 + fft1_re2;
            fft2_im0 <= fft1_im0 + fft1_im2;
            fft2_re2 <= fft1_re0 - fft1_re2;
            fft2_im2 <= fft1_im0 - fft1_im2;

            fft2_re1 <= fft1_re1 + fft2_re3_wn;
            fft2_im1 <= fft1_im1 + fft2_im3_wn;
            fft2_re3 <= fft1_re1 - fft2_re3_wn;
            fft2_im3 <= fft1_im1 - fft2_im3_wn;

            fft2_re4 <= fft1_re4 + fft1_re6;
            fft2_im4 <= fft1_im4 + fft1_im6;
            fft2_re6 <= fft1_re4 - fft1_re6;
            fft2_im6 <= fft1_im4 - fft1_im6;

            fft2_re5 <= fft1_re5 + fft2_re7_wn;
            fft2_im5 <= fft1_im5 + fft2_im7_wn;
            fft2_re7 <= fft1_re5 - fft2_re7_wn;
            fft2_im7 <= fft1_im5 - fft2_im7_wn;

        end
    else
        fft2_en <= 0;
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106

1.3.3 第三级流水线

// 第三级流水线
wire fft3_en1;
wire signed [11:0] fft3_im5_wn;
wire signed [11:0] fft3_re5_wn;
wire signed [47:0] fft3_cmpy35;
assign fft3_re5_wn = fft3_cmpy35[19:8];
assign fft3_im5_wn = fft3_cmpy35[43:32];

cmpy_0 cmpy35(
    .aclk(clk),
    .s_axis_a_tvalid(fft2_en),
    .s_axis_a_tdata({4'd0, fft2_im5, 4'd0, fft2_re5}),
    .s_axis_b_tvalid(1'b1),
    .s_axis_b_tdata({4'd0,12'b0110_0001_1111,4'd0,12'b1110_1100_1000}),
    .m_axis_dout_tvalid(fft3_en1),
    .m_axis_dout_tdata(fft3_cmpy35)
    );

wire fft3_en2;
wire signed [11:0] fft3_im6_wn;
wire signed [11:0] fft3_re6_wn;
wire signed [47:0] fft3_cmpy36;
assign fft3_re6_wn = fft3_cmpy36[19:8];
assign fft3_im6_wn = fft3_cmpy36[43:32];

cmpy_0 cmpy36(
    .aclk(clk),
    .s_axis_a_tvalid(fft2_en),
    .s_axis_a_tdata({4'd0, fft2_im6,4'd0, fft2_re6}),
    .s_axis_b_tvalid(1'b1),
    .s_axis_b_tdata({4'd0,12'b1011_0101_0000,4'd0,12'b1011_0101_0000}),
    .m_axis_dout_tvalid(fft3_en2),
    .m_axis_dout_tdata(fft3_cmpy36)
    );

wire fft3_en3;
wire signed [11:0] fft3_im7_wn;
wire signed [11:0] fft3_re7_wn;
wire signed [47:0] fft3_cmpy37;
assign fft3_re7_wn =fft3_cmpy37[19:8];
assign fft3_im7_wn =fft3_cmpy37[43:32];

cmpy_0 cmpy37(
    .aclk(clk),
    .s_axis_a_tvalid(fft2_en),
    .s_axis_a_tdata({4'd0, fft2_im7,4'd0, fft2_re7}),
    .s_axis_b_tvalid(1'b1),
    .s_axis_b_tdata({4'd0,12'b1110_1100_1000,4'd0,12'b0110_0001_1111}),
    .m_axis_dout_tvalid(fft3_en3),
    .m_axis_dout_tdata(fft3_cmpy37)
    );

reg fft3_en;
reg signed [12:0] fft3_re0;
reg signed [12:0] fft3_im0;
reg signed [12:0] fft3_re1;
reg signed [12:0] fft3_im1;
reg signed [12:0] fft3_re2;
reg signed [12:0] fft3_im2;
reg signed [12:0] fft3_re3;
reg signed [12:0] fft3_im3;
reg signed [12:0] fft3_re4;
reg signed [12:0] fft3_im4;
reg signed [12:0] fft3_re5;
reg signed [12:0] fft3_im5;
reg signed [12:0] fft3_re6;
reg signed [12:0] fft3_im6;
reg signed [12:0] fft3_re7;
reg signed [12:0] fft3_im7;

always@(posedge clk or negedge rst_n) begin
if(!rst_n)
begin
    fft3_en  <= 0;
    fft3_re0 <= 0;
    fft3_im0 <= 0;
    fft3_re1 <= 0;
    fft3_im1 <= 0;
    fft3_re2 <= 0;
    fft3_im2 <= 0;
    fft3_re3 <= 0;
    fft3_im3 <= 0;
    fft3_re4 <= 0;
    fft3_im4 <= 0;
    fft3_re5 <= 0;
    fft3_im5 <= 0;
    fft3_re6 <= 0;
    fft3_im6 <= 0;
    fft3_re7 <= 0;
    fft3_im7 <= 0;
end
else if(fft3_en1 && fft3_en2 && fft3_en3)
begin
    // 实现第三级流水线输出
    fft3_en  <=1'b1;

    fft3_re0 <=fft2_re0 + fft2_re4;
    fft3_im0 <=fft2_im0 + fft2_im4;
    fft3_re4 <=fft2_re0 - fft2_re4;
    fft3_im4 <=fft2_im0 - fft2_im4;

    fft3_re1 <=fft2_re1 + fft3_re5_wn;
    fft3_im1 <=fft2_im1 + fft3_im5_wn;
    fft3_re5 <=fft2_re1 - fft3_re5_wn;
    fft3_im5 <=fft2_im1 - fft3_im5_wn;

    fft3_re2 <=fft2_re2 + fft3_re6_wn;
    fft3_im2 <=fft2_im2 + fft3_im6_wn;
    fft3_re6 <=fft2_re2 - fft3_re6_wn;
    fft3_im6 <=fft2_im2 - fft3_im6_wn;

    fft3_re3 <= fft2_re3 + fft3_re7_wn;
    fft3_im3 <= fft2_im3 + fft3_im7_wn;
    fft3_re7 <= fft3_re3 - fft3_re7_wn;
    fft3_im7 <= fft3_im3 - fft3_im7_wn;
end
else
    fft3_en <= 0;
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119

1.3.4 模块输出

assign data_out_en  = fft3_en; 
assign data_out_re0 = fft3_re0;
assign data_out_im0 = fft3_im0;
assign data_out_re1 = fft3_re1;
assign data_out_im1 = fft3_im1;
assign data_out_re2 = fft3_re2;
assign data_out_im2 = fft3_im2;
assign data_out_re3 = fft3_re3;
assign data_out_im3 = fft3_im3;
assign data_out_re4 = fft3_re4;
assign data_out_im4 = fft3_im4;
assign data_out_re5 = fft3_re5;
assign data_out_im5 = fft3_im5;
assign data_out_re6 = fft3_re6;
assign data_out_im6 = fft3_im6;
assign data_out_re7 = fft3_re7;
assign data_out_im7 = fft3_im7;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

1.4 复数乘法器的ip核

在第二级、第三级流水线中，需要和旋转因子做乘法，于是调用vivado中的复数乘法器IP核（complex multiplier）

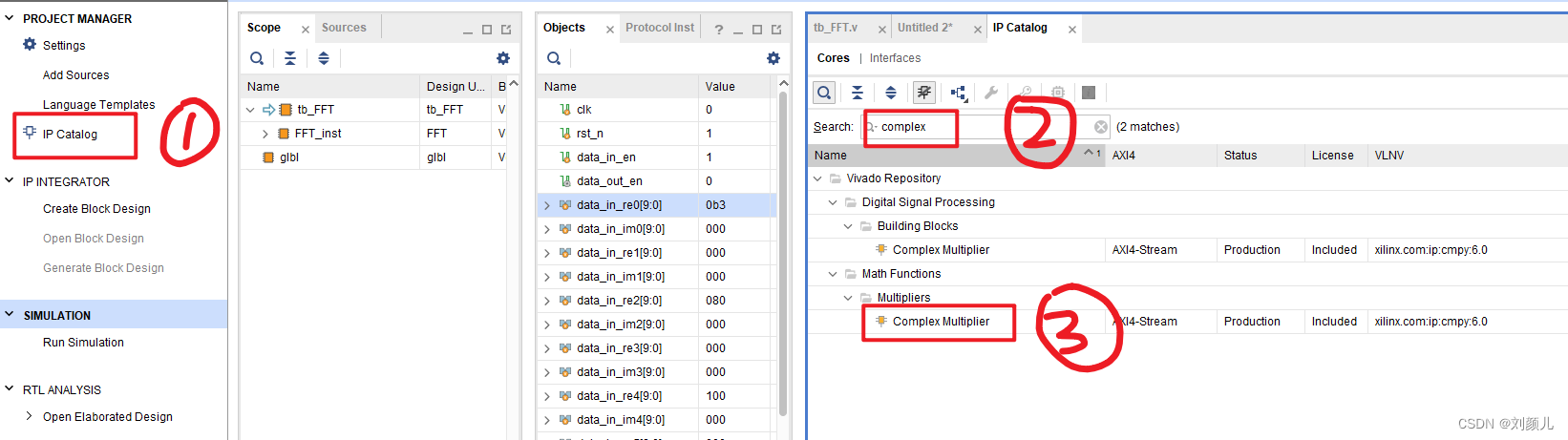
找到后，双击图中的③，就会得到如下图：

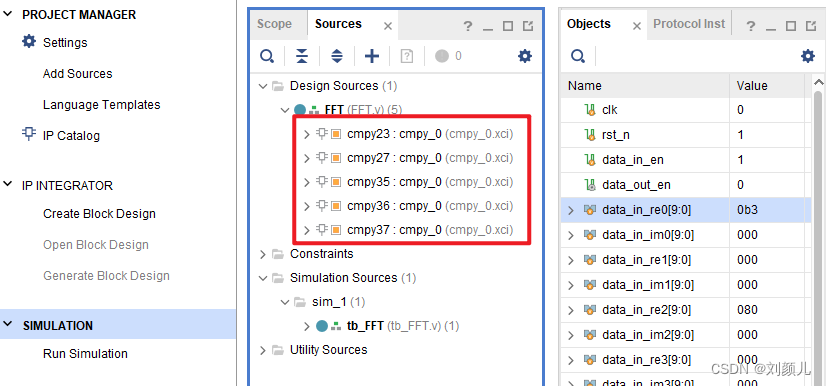
1.5 测试文件

然后将测试文件加入到工程中即可

`timescale 1ns / 1ps
//
// Company: 
// Engineer: 
// 
// Create Date: 2022/06/29 21:15:21
// Design Name: 
// Module Name: tb_FFT
// Project Name: 
// Target Devices: 
// Tool Versions: 
// Description: 
// 
// Dependencies: 
// 
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
// 
//


module tb_FFT();
reg  clk;
reg  rst_n;
reg  data_in_en;
wire data_out_en;
reg [9:0] data_in_re0;
reg [9:0] data_in_im0;
reg [9:0] data_in_re1;
reg [9:0] data_in_im1;
reg [9:0] data_in_re2;
reg [9:0] data_in_im2;
reg [9:0] data_in_re3;
reg [9:0] data_in_im3;
reg [9:0] data_in_re4;
reg [9:0] data_in_im4;
reg [9:0] data_in_re5;
reg [9:0] data_in_im5;
reg [9:0] data_in_re6;
reg [9:0] data_in_im6;
reg [9:0] data_in_re7;
reg [9:0] data_in_im7;

wire [12:0] data_out_re0;
wire [12:0] data_out_im0;
wire [12:0] data_out_re1;
wire [12:0] data_out_im1;
wire [12:0] data_out_re2;
wire [12:0] data_out_im2;
wire [12:0] data_out_re3;
wire [12:0] data_out_im3;
wire [12:0] data_out_re4;
wire [12:0] data_out_im4;
wire [12:0] data_out_re5;
wire [12:0] data_out_im5;
wire [12:0] data_out_re6;
wire [12:0] data_out_im6;
wire [12:0] data_out_re7;
wire [12:0] data_out_im7;


initial clk = 0;
always#5 clk = ~clk;
initial
begin
    rst_n = 0;
    #10
    rst_n = 1;
    data_in_en  = 1;
    data_in_re0 = 10'b0010110011;//0.7
    data_in_im0 = 10'b0000000000;
    data_in_re1 = 10'b0000000000;//0
    data_in_im1 = 10'b0000000000;
    data_in_re2 = 10'b0010000000;//0.5
    data_in_im2 = 10'b0000000000;
    data_in_re3 = 10'b0000000000;//0
    data_in_im3 = 10'b0000000000;
    data_in_re4 = 10'b0100000000;//1I
    data_in_im4 = 10'b0000000000;
    data_in_re5 = 10'b0000000000;//0
    data_in_im5 = 10'b0000000000;
    data_in_re6 = 10'b0000000000;//0
    data_in_im6 = 10'b0000000000;
    data_in_re7 = 10'b0000000000;//0
    data_in_im7 = 10'b0000000000;
end

FFT  FFT_inst(
    . clk(C1k),
    . rst_n(rst_n),
    . data_in_en(data_in_en),
    . data_in_re0(data_in_re0),
    . data_in_im0(data_in_im0),
    . data_in_re1(data_in_re1),
    . data_in_im1(data_in_im1),
    . data_in_re2(data_in_re2),
    . data_in_im2(data_in_im2),
    . data_in_re3(data_in_re3),
    . data_in_im3(data_in_im3),
    . data_in_re4(data_in_re4),
    . data_in_im4(data_in_im4),
    . data_in_re5(data_in_re5),
    . data_in_im5(data_in_im5),
    . data_in_re6(data_in_re6),
    . data_in_im6(data_in_im6),
    . data_in_re7(data_in_re7),
    . data_in_im7(data_in_im7),

    . data_out_en(data_out_en),
    . data_out_re0(data_out_re0),
    . data_out_im0(data_out_im0),
    . data_out_re1(data_out_re1),
    . data_out_im1(data_out_im1),
    . data_out_re2(data_out_re2),
    . data_out_im2(data_out_im2),
    . data_out_re3(data_out_re3),
    . data_out_im3(data_out_im3),
    . data_out_re4(data_out_re4),
    . data_out_im4(data_out_im4),
    . data_out_re5(data_out_re5),
    . data_out_im5(data_out_im5),
    . data_out_re6(data_out_re6),
    . data_out_im6(data_out_im6),
    . data_out_re7(data_out_re7),
    . data_out_im7(data_out_im7)
    );

endmodule

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130

二、FFT在FPGA工程中的应用

后面遇到再补充

三、推荐阅读

1. 文档资料：
   FFT详细介绍教程

2. B站视频：
   B站 - 使用Verilog写FFT
   B站-潘老师-数字信号处理
   B站-FFT公式推导

四、补充

哈哈哈如果有盆友需要工程可以扫下面的马，然后回复：FFT（拖延症的我，等后台收到第一条FFT我再去弄自动回复）
这个公众号是一年前弄好的，现在终于不闲置啦，有了它的用武之地