【R】【支持向量机分类方法】_r语言svm-rfe怎么看

采用 iris 数据集，利用支持向量机算法对鸢尾花的种类进行分类，可视化分类结果并对结果进行分析。

一、安装加载程序包

install.packages("e1071")

library(e1071)
1
2
3

二、数据探索及预处理

data(iris)
summary(iris)

ind<-sample(2,nrow(iris),replace = T,prob = c(0.7,0.3)) 
trainset<-iris[ind==1,] 
testset<-iris[ind==2,]
#三七分

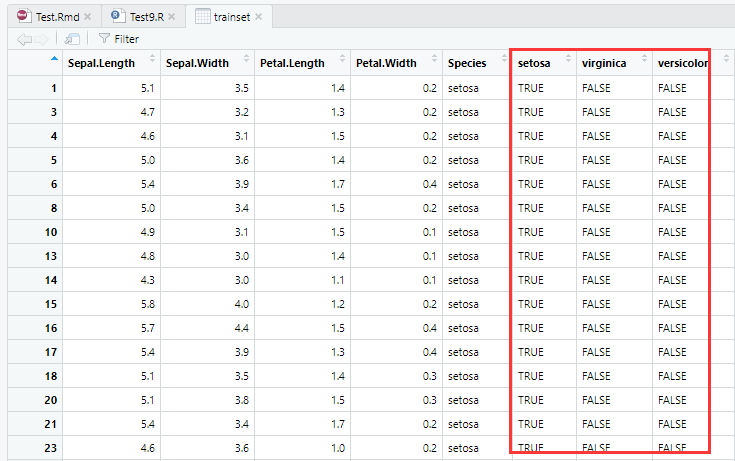
trainset$setosa<-trainset$Species=="setosa"  #山鸢尾
trainset$virginica<-trainset$Species=="virginica"  #维尼吉亚鸢尾
trainset$versicolor<-trainset$Species=="versicolor"  #变色鸢尾
1
2
3
4
5
6
7
8
9
10
11

三、设置特征向量、结果变量

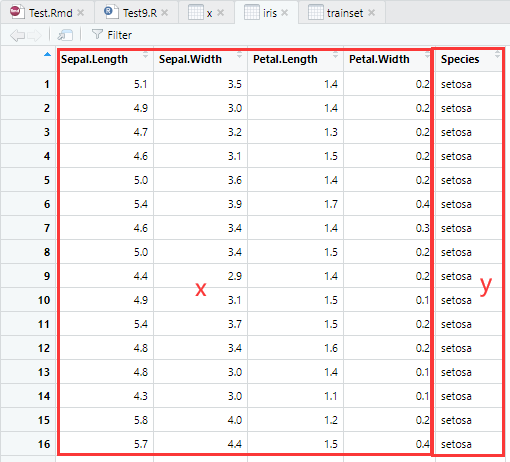
x=iris[,-5] #提取数据中除第 5 列以外的数据作为特征向量 
y=iris[,5] #提取数据中的第 5 列数据作为结果变量
1
2

四、SVM建模分析

model=svm(x,y,kernel="radial") #建立 svm 模型
#kenerl: 核函数选择“radial”

summary(model) #结果分析
1
2
3
4

通过summary()函数可以得到关于模型的相关信息：
SVM-Type项目说明本模型的类别为C-classification（C分类器模型）；
SVM-Kernel项目说明本模型所使用的核函数为radial（高斯内积函数）；
cost项目说明本模型确定的约束违反成本为1。

对于该数据，模型找到了51个支持变量：
第一类具有8个支持向量，第二类具有22个支持向量，第三类具有21个支持向量。

Class说明模型中的三个类别为：setosa、versicolor和virginica。

五、预测

x=iris[,1:4] #需要进行预测的样本特征矩阵

pred=predict(model,x) #根据模型 model 对 x 数据进行预测

pred[sample(1:150,8)] #随机挑选 8 个结果进行展示
1
2
3
4
5

在进行数据预测时，主要注意的问题就是必须保证用于预测的特征向量的个数应同模型建立时使用的特征向量个数一致（即建模时x特征向量与预测时x特征向量个数一致），否则将无法预测结果。在使用predict()函数进行预测时，不用刻意去调整预测结果类型。

通过对预测结果的展示，我们可以看到predict()函数在预测时自动识别预测结果的类型，并自动生成了相应的类别名称。

六、模型精度

通常在进行预测之后，还需要检查模型预测的精度，需要用到table()函数对预测结果和真实结果做出对比展示：

table(pred,y) #模型预测精度展示
1

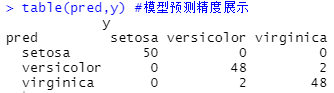
通过观察table()函数对模型预测精度的展示结果可以看到在模型预测时，（竖着看）
模型将所有属于setosa类型的花全部预测正确；
模型将属于versicolor类型的花中的48朵预测正确，但将2朵误预测为virginica类型；
模型将属于virginica类型的花中的48朵预测正确，但将2朵误预测为versicolor类型。

七、优化模型（提高模型精度）

分析数据可以看出，数据需要判别的是三个类别，且三个类别属于字符类型。
所以我们可以选择的支持向量机分类机就有三类：C-classification、nu-classification、one-classification。
可以选择的核函数有四类：线性核函数(linear)、多项式核函数(polynomial)、径向基核函数(radial basis,RBF)和神经网络核函数(sigmoid)。
所以在时间和精力允许的情况下，应该尽可能建立所有可能的模型，最后通过比较选出判别结果最优的模型。
下面通过for循环进行全部的排列组合：

attach(iris)  #建立iris数据的连接

x=subset(iris,select=-Species)  #样本特征向量
y=Species  #样本结果变量

type=c("C-classification","nu-classification","one-classification")
#全部分类向量机方式

kernel=c("linear","polynomial","radial","sigmoid")
#全部核函数种类

pred=array(0,dim=c(150,3,4)) 
#预测结果矩阵，初始化预测结果矩阵的三维长度分别为150,3,4

accuracy=matrix(0,3,4) 
#模型精准度矩阵，初始化模型精准度矩阵的二维分别为3,4

yy=as.integer(y)
#为方便模型精度计算，将结果变量（y）数量化为1,2,3

for(i in 1:3){
  #确认j影响的维度代表核函数
  for(j in 1:4){
    #对每一模型进行预测
    pred[,i,j] = predict(svm(x,y,type=type[i],kernel=kernel[j]),x)
    #对每一模型进行预测，其中 svm(x,y,type=type[i],kernel=kernel[j]) = model
    if (i>2)accuracy[i,j] = sum(pred[,i,j]!=1)
      #one-classification的判断方式不同
    else 
      accuracy[i,j] = sum(pred[,i,j]!=yy)
      #“pred[,i,j]!=yy”即预测错误的数据
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

在运行程序中，if语句的使用是因为C-classification和nu-classification与one-classification的模型预测精度计算方式不同，所以应该分别进行计算。

在运行程序之后，可以得到所有12（3*4）个模型所对应的预测精度。程序中accuracy所代表的是模型预测错误的个数。

我们将根据这个预测结果挑选出预测错误最少的一些模型，然后再根据实际情况进行详细分析，最终决定得出最适合本次研究目的的模型。

for循环的warning messages不用在意：

dimnames(accuracy)=list(type,kernel)
#确定模型精度变量的列名和行名

table(pred[,1,3],y)
1
2
3
4

可以手动查看每个accuracy，或者查看结果的数组：

从表中的模型预测结果可以看出，利用one-classification方式无论采取何种核函数得出的结果错误都非常多，所以可以看出该方式不适合这类数据类型的判别。

因为使用one-classification方式进行建模时，数据通常情况下为一个类别的特征，建立的模型主要用于判别其他样本是否属于这类。

利用C-classification+radial（高斯核函数）结合的模型判别错误最少，如果我们建立模型的目的主要是为了总体误判率最低，并且各种类型判错的代价是相同的，那么就可以直接选择这个模型作为最有模型。

那么将利用C-classification与高斯核函数介个的模型的预测结果示例代码如下：

在得到这个较优模型之后，针对这一模型在进行具体的分析和讨论，力图进一步提高模型的预测精度。

八、可视化分析

在建立支持向量机模型之后，进一步分析模型。

在分析过程中将会使用模型可视化以便于对模型的分析。在对模型进行可视化的过程中，我们使用plot()函数对模型进行可视化绘制：

plot(cmdscale(dist(iris[,-5])),col=c("red","black","gray")[as.integer(iris[,5])],pch=c("o","+")[1:150%in% model$index + 1]) 

legend(2,0.8,c("setosa","versicolor","virginica"),col=c("red","black","gray"),lty=1)
#添加图例
1
2
3
4

plot函数注释：

plot
(
cmdscale(dist(iris[,-5])),
#dist默认是算欧式距离，算完后得到一个所有距离的矩阵，传给cmdscale()函数
col=c("red","black","gray")[as.integer(iris[,5])],
#将结果变量转换为整数并按颜色设置
pch=c("o","+")[1:150 %in% model$index + 1]
#设置点样式，%in%相当于match()函数的一个缩写，判断一个数组或矩阵是否包含在另一个数组或矩阵里。
#如果在model矩阵里则标记为“+”，否则标记为“o”
) 
1
2
3
4
5
6
7
8
9
10

cmdscale函数注释：

数据矩阵的经典多维缩放 （MDS）

cmdscale(d, k = 2, eig = FALSE, add = FALSE, x.ret = FALSE,
         list. = eig || add || x.ret)
1
2

• d：距离结构，例如返回的距离结构或包含差异的完全对称矩阵。

legend图例函数注释：

legend(x, y, legend, col, lty)
1

• x，y：用于定位图例的 x 和 y 坐标。
• legend：字符或表达式向量，显示在图例中。
• col：图例中显示的点或线的颜色。
• lty， lwd：图例中显示的线条的线条类型和宽度，如果是画线必须指定两个中的一个。

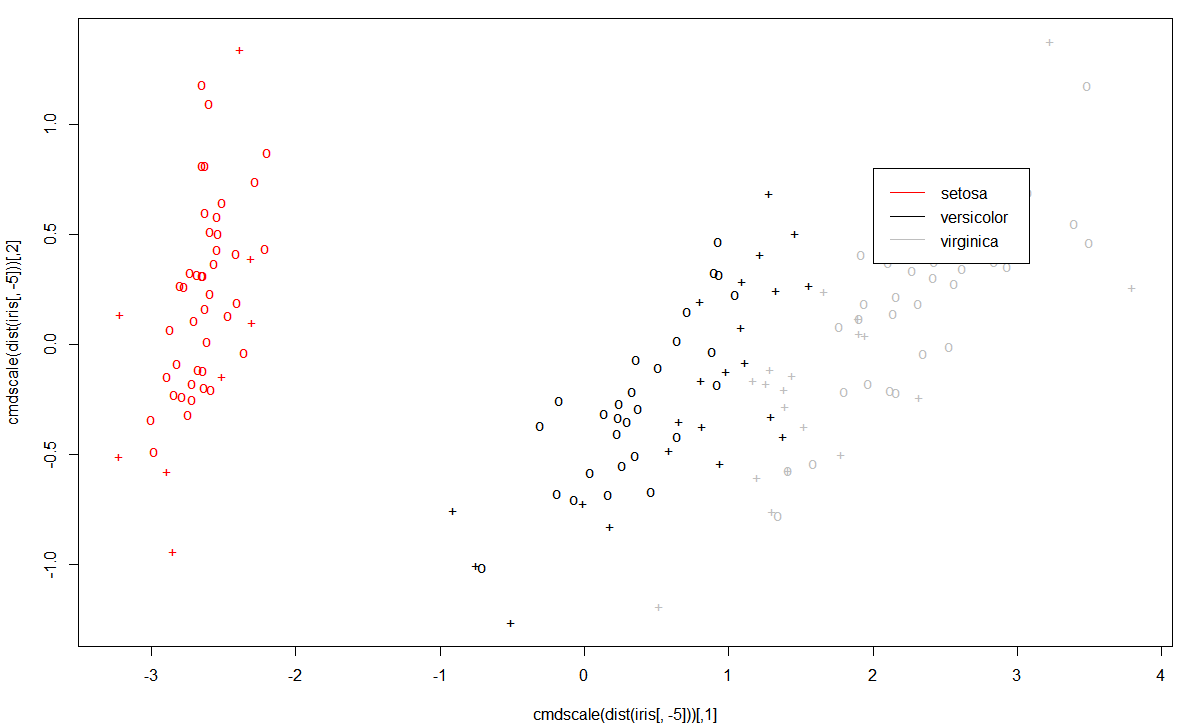
通过plot()函数对所建立的支持向量机模型进行可视化之后，所得到的图像是对模型数据类别的一个总体观察。

图中"+"表示的是支持向量，“o”表示的是普通样本点。

从图中我们可以看到，鸢尾属中的第一种setosa类别同其他两种区别较大，而剩下的versicolor和virginica类别却相差很小，甚至存在交叉难以区分。

这也在另一个角度解释了在模型预测过程中出现的问题，这正是为什么模型将两朵versicolor类别的话预测成了virginica类别，并将两朵virginica类别的花预测成了versicolor类别的原因。

九、特征变量变动过程

在使用plot()函数对所建立的模型进行了总体的观察后，我们还可以利用plot()函数对模型进行其他角度的可视化分析。

我们可以利用plot()函数对模型类别关于模型中任意两个特征向量的变动过程进行绘图。绘图过程如下：

data(iris)

model=svm(Species~.,data=iris) #利用公式的格式建立模型

plot(model,iris,Petal.Width~Petal.Length,fill=FALSE,symbolPalette=c("red","black","grey"),svSymbol="+") 
#绘制模型类别关于花宽度和长度的分类情况

legend(1,2.5,c("setosa","versicolor","virginica"),col=c("red","black","gray"),lty=1) 
#添加图例
1
2
3
4
5
6
7
8
9

plot函数注释：

plot
(
model,
#训练好的模型
iris,
#数据集
Petal.Width~Petal.Length,
#属性：花瓣宽度与花瓣长度
fill=FALSE,
#不使用颜色填充背景
symbolPalette=c("red","black","grey"),
#点的颜色
svSymbol="+"
#支持向量使用"+"表示
) 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

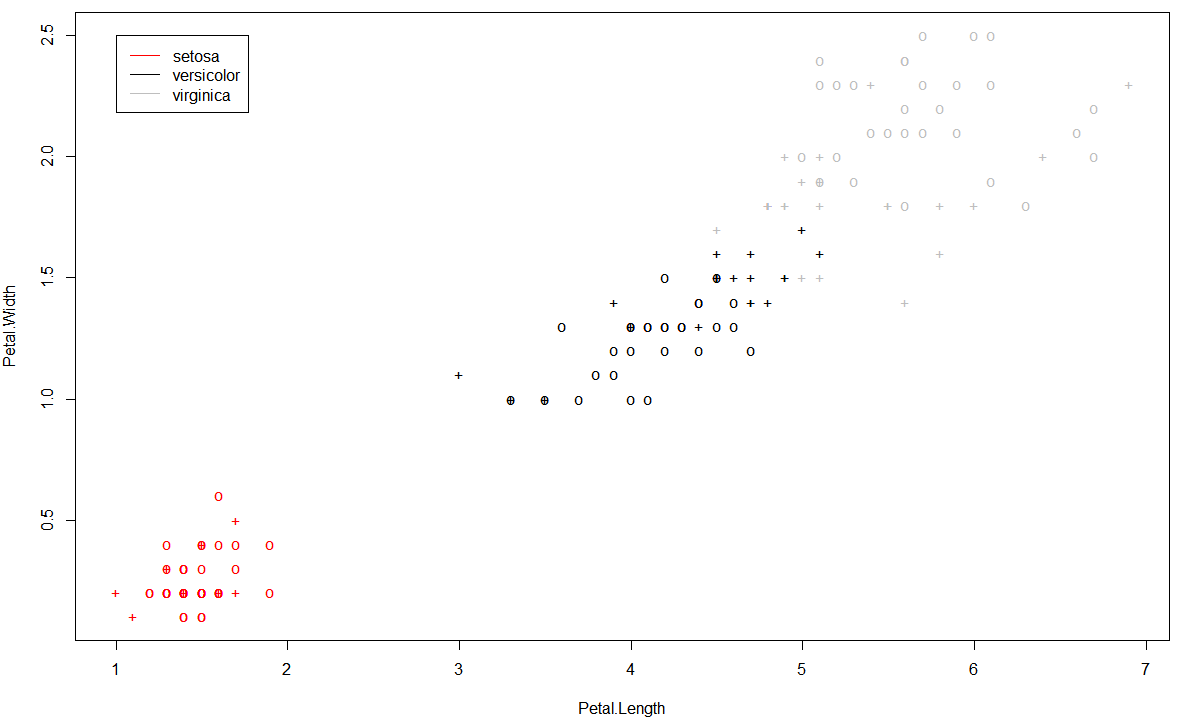
通过对模型关于花瓣的宽度和长度对模型类别分类影响的可视化后，我们仍然可以得到一致的结果：
setosa类别的花瓣同另外两个类别相差较大，而versicolor类别的花瓣同virginica类别的花瓣相差较小。

通过模型可视化可以看出，virginica类别的花瓣在长度和宽度的总体水平上都高于其他两个类别，而versicolor类别的花瓣在长度和宽度的总体水平上处于居中的位置，而setosa类别的花瓣在长度和宽度上都比另外两个类别小。

十、优化模型

在模型预测精度结果中我们发现，尽管模型的预测错误已经很少，但是所建立的模型还是出现了4个预测错误，那么为了寻找到一个最优的支持向量机模型，我们是否能通过一些方式来进一步提高模型的预测精度，最理想的情况就是将模型的预测错误率减少为零。

通过对模型的可视化分析后，无论是从总体的角度观察，还是从模型个别特征的角度观察，我们都可以得到一致的结论：类别setosa同其他两个类别的差异较大，而类别versicolor和类别virginica的差异非常小，而且直观上能看到两部分出现少许交叉，并且在预测结果中，模型出现判别错误的地方也是混淆了类别versicolor和类别virginica。

因此，针对这种情况，可以通过改变模型各个类别的比重来对数据进行调整。

由于类别setosa同其他两个类别相差很大，所以我们可以考虑降低类别setosa在模型中的比重，而提高另外两个类别的比重，即适当牺牲类别setosa的精度来提高其他两个类别的精度。

这种方法在R语言中可以通过svm()函数中的class.weights参数来进行调整。特别强调的是，class.weights参数所需要的数据必须为向量，并且具有列名，具体过程如下：

wts <- c(1,1,1)
#确定模型各个类别的比重为1:1:1

names(wts) <- c("setosa","versicolor","virginica")
#确定各个比重对应的类别

model1 <- svm(x,y,class.weights = wts)
#建立模型
1
2
3
4
5
6
7
8

当模型的各个类别的比重为1:1:1时，则模型就是最原始的模型，预测结果即之前的预测模型。

接下来我们适当提高类别versicolor和类别virginica的比重，以观察对模型的预测精度是否产生影响，是否为正向影响。

首先，我们先将这两种类别的比重扩大100倍（具体倍数可根据自行调整修改）:

wts <- c(1,100,100)

names(wts) <- c("setosa","versicolor","virginica")

model2 <- svm(x,y,class.weights = wts)

pred2 <- predict(model2,x)

table(pred2,y)
1
2
3
4
5
6
7
8
9

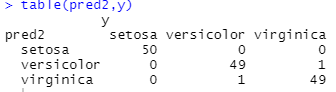
通过预测结果的展示发现，通过提高类别versicolor和virginica的比重却能能对模型的预测精度产生影响，并且能产生正向影响。

所以我们可以继续通过改变权重的方法来提高模型的预测精度。

接下来，我们将这两个类别的权重再扩大5倍，即相对于原始数据，这两个类别的权重总共扩大了500倍：

wts <- c(1,500,500)

names(wts) <- c("setosa","versicolor","virginica")

model3 <- svm(x,y,class.weights = wts)

pred3 <- predict(model3,x)

table(pred3,y)
1
2
3
4
5
6
7
8
9

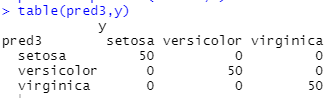
通过对权重的调整之后，我们建立的支持向量机模型能够将所有样本全部预测正确。

所以在实际构建模型的过程中，在必要的时候可以通过改变各样本之间的权重比例来提高模型的预测精度。

支持向量机可以提高泛化性能，解决高维问题，它可以解决非线性问题和小样本情况下的机器学习问题。

但是支持向量机对缺失数据敏感，并且对非线性问题没有通用解决方案，必须谨慎选择 Kernelfunction 来处理。

Reference

强推：利用R语言实现支持向量机（SVM）数据挖掘案例/文博客园@小人物001

r语言 svm 大样本_利用R语言实现支持向量机（SVM）数据挖掘案例/文CSDN@weixin_39907939

核函数&径向基核函数 (Radial Basis Function)–RBF/文CSDN@Paul-Huang

【机器学习】支持向量机 SVM（非常详细）/文知乎@阿泽

（R语言）SVM的原理及入门使用（详细）/文CSDN@菊次郎的夜

R语言实现支持向量机SVM应用案例/文html中文网

SVM算法及案例分析（SVM分类、SVM回归）/文博客园@zhang-X

R语言中MDS的使用/文知乎@超爱学习

R语言 legend()用法及代码示例/文纯净天空

legend: Add Legends to Plots/文RDocumemtation