AllinToyou

这个屌丝很懒，什么也没留下！

热门标签

2.2 SIMPLE系列算法 | 2.3 PISO算法（OpenFOAM理论笔记系列）

作者：AllinToyou | 2024-05-03 11:12:54

踩

piso算法

2.2 SIMPLE系列算法

2.2.1标准SIMPLE算法

SIMPLE算法(Semi-Implicit Method for PressureLinked Equations)¹最初被设计用来求解稳态问题，即控制方程中不包含瞬态项的计算。按照1.3.3节的约定，我们假设计算开始的时候有初始的压力和速度值 $P^o,\vec{U^o}$ ,待求的真值为 $P^n,\vec{U^n}$ 。实际上，速度的初始值可以完全随意给定，因为我们完全首先可以将初始压力带入式2.1解出一个速度:
$a_P\vec U_p^r+\sum_Na_N\vec U_N^r=\vec S-\nabla P^o \tag{2.13}$
上述步骤称为动量预测，解得的速度 $U^r$ 称为预测速度。

预测速度并不是待求的真实速度，根据式上一节的推导，待求速度和待求压力之间满足压力泊松方程：
$\nabla\cdot\left(\frac{1}{a_P}\nabla P^n\right)=\nabla\cdot\left(\vec{HbyA^n}\right) \tag{2.6}$
显然， $HbyA^n$ 是 $\vec{U^n}$ 的函数，知道 $\vec{U^n}$ 我们就能算出待求的压力 $P^n$ ,但目前我们只有求解式(2.13)得到的 $\vec U^r$ ,SIMPLE算法在这里做了一个妥协与假设，其用 $\vec U^r$ 代替 $\vec{U^n}$ 计算 $P^n$ ，即：
$\nabla\cdot\left(\frac{1}{a_P}\nabla P^n\right)=\nabla\cdot\left(\vec{HbyA^r}\right) \tag{2.14}$
其本质上是将方程(2.4)转化为
$\vec U_p^n=\vec{HbyA^r}-\frac{1}{a_P}\nabla P^n \tag{2.15}$
再带入连续性方程后进行离散得到的。式(2.15)当然是不精确的，在下一节中我们将分析式(2.15)中做出的简化的背后含义。同时，式(2.15)还可以用来根据式2.14解出的压力来更新速度以得到 $U^n$ 。这样，我们先通过求解式(2.13)得到预测速度 $\vec U^r$ ，再根据式2.13得到待求压力 $P^n$ ，最后根据式2.15更新现有的速度得到 $\vec U^n$ 。由于式(2.14)是不准确地，因此我们计算得到的 $P^n$ 和 $\vec U^n$ 也是不准确的，我们将 $P^n$ 和 $\vec U^n$ 作为新的 $P^o$ 和 $\vec U^o$ 重新进行上述过程，直到计算收敛为止。

SIMPLE算法的流程图如下：

图2.1 稳态SIMPLE算法框图

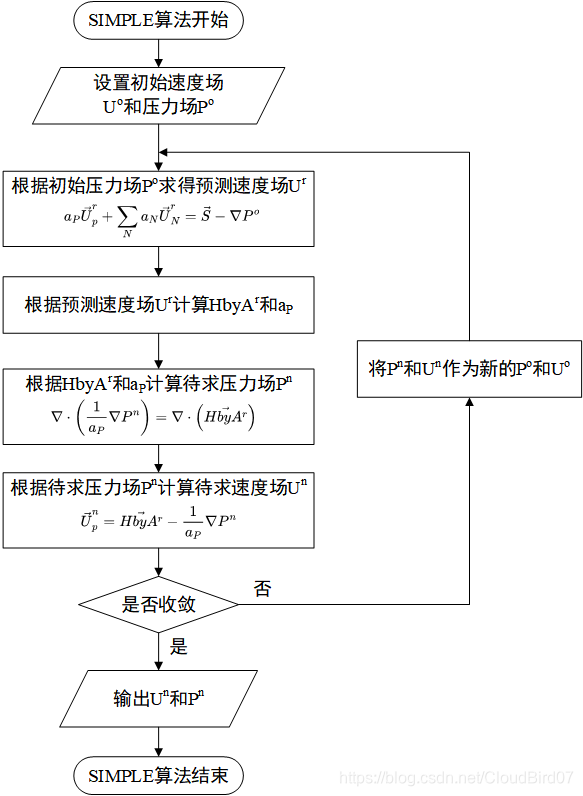
2.2.2 SIMPLE算法的亚松弛

在上一节中，我们指出SIMPLE算法唯一的简化假设是将式(2.4)简化为了式(2.15)，在这一节我们详细分析一下这一简化背后的逻辑。
为了方便表述，我们将式(2.13)中的压力 $P_o$ 改写为 $P_r$ ,表示为预测压力。
$a_P\vec U_p^r+\sum_Na_N\vec U_N^r=\vec S-\nabla P^r \tag{2.16}$
对于待求的压力和速度，同样存在着上述关系，即式2.1：
$a_P\vec U_p^n+\sum_Na_N\vec U_N^n=\vec S-\nabla P^n \tag{2.1}$
使用式(2.1)减式(2.16)可得：
$a_P\vec U_p^*+\sum_Na_N\vec U_N^*=-\nabla P^* \tag{2.17}$
其中， $\vec U^*=\vec U^n-\vec U^r$ ， $P^*=P^n-P^r$ ,分别表示修正速度和修正压力，它们是真实值与当前计算值的差。SIMPLE算法认为，在计算过程中可以略去相邻点修正带来的影响，即将式(2.17)简化为：
$a_P\vec U_p^*=-\nabla P^* \tag{2.17}$
将式2.17与式2.16相加即可得到SIMPLE算法中使用的式(2.15)。

这一略去相邻点修正的假设通常称为略去邻点假设，这一假设是非常激进(粗暴)的，在有些情况会导致速度和压力的修正过于剧烈，使模拟发散。解决这一问题最好的办法是使用亚松弛技术(under-relax)。

假设一次SIMPLE循环开始时候的初始值为 $\vec {U^o}$ 和 $P^o$ ,这次循环结束后得到的计算值为 ${\vec U}^{tem}$ ， $P^{tem}$ ，我们并不使用计算值作为最终得到的值，而是使用下面的值作为最终计算得到的值:

\begin{array}{l} {\vec{U}}^{n} = {\vec{U}}^{o} + α_{U} ({\vec{U}}^{t e m} - {\vec{U}}^{o}) \\ P^{n} = P^{o} + α_{P} (P^{t e m} - P^{o}) \end{array}

$\begin{array}{l} {\vec U^n}={\vec U^o}+\alpha_U\left({\vec U^{tem}}-{\vec U^o} \right) \\ {P^n}={P^o}+\alpha_P\left({P^{tem}}-{P^o} \right) \end{array}$ \tag{2.18}

U^{n} = U^{o} + α_{U} (U^{t e m} - U^{o}) P^{n} = P^{o} + α_{P} (P^{t e m} - P^{o}) (2.18)

式(2.18)中

\alpha

为亚松弛因子，其值在0和1之间进行选择。显然，当

\alpha=1

时，我们将完全采用计算得到的值作为最终的值，但正如前面所提到的，这样做往往会导致修正过大，计算发散。如果

\alpha=0

，我们则将完全将旧值赋值给新值，这样相当于没做计算，也是不可取的。整体来说，

\alpha

愈趋近于1，表示速度和压力修正得越激进，越容易导致发散但如果可以收敛其会使用较少的迭代步，也就是计算效率较高。当

\alpha

趋近于0时，计算不容易发散，但是会需要更多的迭代步来达到收敛，计算效率会降低。合适的

\alpha

选择应该兼顾结果的收敛性和计算的效率。

2.2.3 SIMPLEC算法

SIMPLEC(SIMPLE-Consistent)算法²是一类修正的SIMPLE算法，其也认为SIMPLE算法中的略去邻点假设过于激进，为了避免这种激进的假设，其没有采用亚松弛技术，而是做了以下修正：

首先，SIMPLEC算法认为当前点的修正速度应该是相邻点修正速度的平均，即：
$\vec U_p^*=\frac{\sum a_N\vec U_N^*}{\sum a_N} \tag{2.19}$
将式2.19带入修正量的方程2.17可得：
$a_P\vec U_p^*+\left(\sum_Na_N\right) \vec U_p^* =-\nabla P^* \tag{2.20}$
整理可得：
$\vec U_p^* =-\frac{1}{a_P+\sum_Na_N}\nabla P^* \tag{2.21}$
在有限体积法中， $\sum_Na_N$ 为负值，因此，在相同的U_p^*时，使用2.21得到的修正压力要比式(2.17)小。将式(2.21)与式(2.16)相加可得：
$a_P\vec U_p^n+\sum_Na_N\vec U_N^r=\vec S-\nabla P^r-\frac{a_P}{a_P+\sum_Na_N}\nabla P^* \tag{2.22}$
整理可得：

\begin{array}{l} {\vec{U}}_{p}^{n} = \frac{\vec{S}}{a_{P}} - \frac{\sum_{N} a_{N} {\vec{U}}_{N}^{r}}{a_{P}} - \frac{1}{a_{P}} \nabla P^{r} - \frac{1}{a_{P} + \sum_{N} a_{N}} \nabla P^{*} \\ = {\vec{H b y A}}^{r} - \frac{1}{a_{P}} \nabla P^{r} - \frac{1}{a_{P} + \sum_{N} a_{N}} \nabla P^{*} \\ = {\vec{H b y A}}^{r} - \frac{1}{a_{P}} \nabla P^{r} - \frac{1}{a_{P} + \sum_{N} a_{N}} \nabla P^{*} + \frac{1}{a_{P} + \sum_{N} a_{N}} \nabla P^{r} - \frac{1}{a_{P} + \sum_{N} a_{N}} \nabla P^{r} \\ = {\vec{H b y A}}^{r} + (\frac{1}{a_{P} + \sum_{N} a_{N}} - \frac{1}{a_{P}}) \nabla P^{r} - \frac{1}{a_{P} + \sum_{N} a_{N}} \nabla P^{n} \end{array}

$\begin{array}{l} \vec U_p^n=\frac{\vec S}{a_P}-\frac{\sum_Na_N\vec U_N^r}{a_P}-\frac{1}{a_P}\nabla P^r-\frac{1}{a_P+\sum_Na_N}\nabla P^* \\ \\ =\vec {HbyA}^r-\frac{1}{a_P}\nabla P^r-\frac{1}{a_P+\sum_Na_N}\nabla P^* \\ \\ =\vec {HbyA}^r-\frac{1}{a_P}\nabla P^r-\frac{1}{a_P+\sum_Na_N}\nabla P^*+\frac{1}{a_P+\sum_Na_N}\nabla P^r-\frac{1}{a_P+\sum_Na_N}\nabla P^r \\ \\ =\vec {HbyA}^r+\left(\frac{1}{a_P+\sum_Na_N}-\frac{1}{a_P}\right)\nabla P^r-\frac{1}{a_P+\sum_Na_N}\nabla P^n \end{array}$ \tag{2.23}

U_{p}^{n} = \frac{S}{a _{P}} - \frac{\sum _{N} a _{N} U _{N}^{r}}{a _{P}} - \frac{1}{a _{P}} \nabla P^{r} - \frac{1}{a _{P} + \sum _{N} a _{N}} \nabla P^{*} = H b y A^{r} - \frac{1}{a _{P}} \nabla P^{r} - \frac{1}{a _{P} + \sum _{N} a _{N}} \nabla P^{*} = H b y A^{r} - \frac{1}{a _{P}} \nabla P^{r} - \frac{1}{a _{P} + \sum _{N} a _{N}} \nabla P^{*} + \frac{1}{a _{P} + \sum _{N} a _{N}} \nabla P^{r} - \frac{1}{a _{P} + \sum _{N} a _{N}} \nabla P^{r} = H b y A^{r} + (\frac{1}{a _{P} + \sum _{N} a _{N}} - \frac{1}{a _{P}}) \nabla P^{r} - \frac{1}{a _{P} + \sum _{N} a _{N}} \nabla P^{n} (2.23)

将式2.23带入连续性方程即可得到压力泊松方程：

\nabla\cdot\left(\frac{1}{a_P+\sum_Na_N}\nabla P^n \right)=\nabla\cdot\left[\vec {HbyA}^r+\left(\frac{1}{a_P+\sum_Na_N}-\frac{1}{a_P}\right)\nabla P^r \right] \tag{2.24}

SIMPLEC算法与SIMPLE算法的流程完全一致，仅是将式(2.14)替换为式(2.24)，将式(2.15)替换为式(2.23)。

SIMPLE算法还有另一种修正版本，称为SIMPLER算法，另外，SIMPLE算法还可以拓展到瞬态计算中，称为瞬态SIMPLE算法，由于OpenFOAM中不涉及这两类算法，我们在这里不做介绍，有兴趣的读者可以参考相关文献³⁴。关于SIMPLE和SIMPLEC算法的内容除了参考原始文献也可以参考文献⁵.

2.2.4 OpenFOAM中的SIMPLE算法

2.2.4.1 simpleFoam代码解析

simpleFoam是OpenFOAM中使用SIMPLE算法的最经典的求解器，在这一节我们对其代码进行解析。

在代码解析中，我们对OpenFOAM自带的注释进行翻译，翻译内容以“译：”开头，对于我们自己的解释内容则以"释："开头。

代码1 simpleFoam代码解读
simpleFoam.C:

#include "fvCFD.H"
//释：OpenFOAM最基础的库文件，必须包含
#include "singlePhaseTransportModel.H"
//释：导入单相流体输运模型库
#include "turbulentTransportModel.H"
//释：导入湍流模型库
#include "simpleControl.H"
//释：导入SIMPLE算法的控制库
#include "fvOptions.H"
//释：导入处理源项的库

//释：上述文件为程序运行的必要库文件，每个库文件的作用及详细信息用户可以查找对应的原代码查看

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

int main(int argc, char *argv[])
{
    #include "postProcess.H"
    //释：导入用于后处理相关功能的库

    #include "setRootCaseLists.H"
    //释：导入与算例目录设置相关的库
    #include "createTime.H"
    //释：创建时间相关对象
    #include "createMesh.H"
    //释：创建网格相关对象
    #include "createControl.H"
    //释：创建算法控制相关对象
    #include "createFields.H"
    //释：创建并初始化速度场，压力场等变量。
    #include "initContinuityErrs.H"
    //释：初始化计算连续性方程模拟误差的相关代码

    turbulence->validate();
    //湍流模型相关功能

    // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

    Info<< "\nStarting time loop\n" << endl;

    while (simple.loop(runTime))
    //SIMPLE算法主循环
    {
        Info<< "Time = " << runTime.timeName() << nl << endl;

        // --- Pressure-velocity SIMPLE corrector
        //译：SIMPLE压力速度修正代码
        {
            #include "UEqn.H"
            //求解速度方程，这部分代码之后详解
            #include "pEqn.H"
            //求解压力方程，这部分代码之后详解
        }

        laminarTransport.correct();
        turbulence->correct();
        //输运模型与湍流模型的计算修正代码

        runTime.write();
        //写出需要输出的场

        Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << " s"
            << "  ClockTime = " << runTime.elapsedClockTime() << " s"
            << nl << endl;
    }

    Info<< "End\n" << endl;

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

UEqn.H:

// Momentum predictor
//译：动量预测代码

MRF.correctBoundaryVelocity(U);
//用来处理旋转坐标系下的速度修正

tmp<fvVectorMatrix> tUEqn
(
    fvm::div(phi, U)
    + MRF.DDt(U)
    + turbulence->divDevReff(U)
    //释： turbulence->divDevReff(U)即扩散项，因为湍流模型，流变模型等代码实际上是对扩散项进行修正，因此在OpenFOAM中扩散项的计算归于湍流模型的代码中。
    ==
    fvOptions(U)
);
fvVectorMatrix& UEqn = tUEqn.ref();
//释：上述代码离散了不包含压力的动量方程，本质上是组建了式(2.8)的矩阵系统，为之后通过式(2.9)和式(2.10)计算HbyA做准备。

UEqn.relax();
// 释： 速度方程进行亚松弛

fvOptions.constrain(UEqn);

if (simple.momentumPredictor())
{
    solve(UEqn == -fvc::grad(p));

    fvOptions.correct(U);
}
//释： 求解动量预测方程(2.13),simple.momentumPredictor()将读取算法配置字典中的momentumPredictor选项，如果不设置该项，默认为true，即进行动量预测步骤
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

pEqn.H

{
    volScalarField rAU(1.0/UEqn.A());
    //释： 计算1/aP，其中UEqn.A()获得Ap，从矩阵的角度看即是由系数矩阵的对角线元素组成的矩阵
    volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p));
    surfaceScalarField phiHbyA("phiHbyA", fvc::flux(HbyA));
    //释： 计算HbyA，即式(2.9)至(2.10)的过程
    MRF.makeRelative(phiHbyA);
    //释： MRF为旋转坐标系相关内容
    adjustPhi(phiHbyA, U, p);

    tmp<volScalarField> rAtU(rAU);

    if (simple.consistent())
    {
        rAtU = 1.0/(1.0/rAU - UEqn.H1());
        phiHbyA +=
            fvc::interpolate(rAtU() - rAU)*fvc::snGrad(p)*mesh.magSf();
        HbyA -= (rAU - rAtU())*fvc::grad(p);
    }
    //释： 在上述代码中，simple.consistent()会读取simple算法配置字典中的consistent字段(默认为false)，如果其为true，表示使用SIMPLEC算法，if括号中的内容是组建SIMPLEC算法中的相关系数， rAtU为式(2.24)左侧括号内的系数，HbyA也将更新为式(2.24)右侧中括号中的内容。

    tUEqn.clear();

    // Update the pressure BCs to ensure flux consistency
    //译：更新压力边界条件以保证通量计算守恒
    constrainPressure(p, U, phiHbyA, rAtU(), MRF);

    // Non-orthogonal pressure corrector loop
    //译：非正交修正循环
    while (simple.correctNonOrthogonal())
    {
        fvScalarMatrix pEqn
        (
            fvm::laplacian(rAtU(), p) == fvc::div(phiHbyA)
        );
        //释：组建压力泊松方程

        pEqn.setReference(pRefCell, pRefValue);
        //释：设置压力参考点与压力参考值

        pEqn.solve();
        //释：求解压力泊松方程

        if (simple.finalNonOrthogonalIter())
        {
            phi = phiHbyA - pEqn.flux();
        }
        //释：在最后一次非正交修正结束后更新速度，即计算式(2.15)或式(2.24)，但这里更新的是速度的通量，而不是速度本身
    }

    #include "continuityErrs.H"
    // 释：计算连续性方程计算误差

    // Explicitly relax pressure for momentum corrector
    //译：压力场进行显示亚松弛
    p.relax();
    //释：压力场进行亚松弛

    // Momentum corrector
    //释：动量修正
    U = HbyA - rAtU()*fvc::grad(p);
    //释：直接更新速度，即计算式(2.15)或式(2.24)
    U.correctBoundaryConditions();
    fvOptions.correct(U);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

2.2.4.2 SIMPLE算法设置

在OpenFOAM中，SIMPLE算法的求解控制在fvSolutions字典中进行，主要有以下几个项目：

SIMPLE子字典
- nNonOrthogonalCorrectors字段
  nNonOrthogonalCorrectors字段用于设置非正交修正循环的次数，关于非正交修正的原因我们将在第三章中进行分析。对于正交性较好的网格，可以不进行非正交修正，对于网格正交性不好的网格可以设置2-3次的非正交修正次数。然而推荐无论网格正交性怎样，至少进行1次非正交循环。从代码分析中可以看出，非正交循环的主要工作是重复求解压力泊松方程，实际模拟中求解压力泊松方程的次数为非正交修正循环次数+1。
- consistent字段
  consistent字段用于指定是否采用SIMPLEC算法，如果其值为true则表示采用SIMPLEC算法。其值默认为false。
- pRefCell和pRefValue字段
  对于一个封闭的不可压缩体系，压力的绝对值并不重要，重要的是相对压力。用户可以给编号为pRefCell的网格参考压力值pRefValue，一般两个值都可以设置为0。这两个字段是必须设置的字段，如果不设置求解器会运行报错。
  陶文铨院士在《数值传热学》中对相对压力值的设定有过非常经典的叙述：
  “对于不可压缩流体的流场计算，我们所关心的是流场中各点之间的压力差而不是其绝对值。流体的绝对压力常比流经计算区域的压差要高几个数量级，如果维持在压力接对峙的水平上进行数值计算，则压差的计算就会导致较大的相对误差。为了减少压力计算中的舍入误差，可以适当地选择流畅中某点的绝对压力为零，而所有其他点的压力都是对该参考点而言的。采用这种做法时，数值计算所得的压力场会出现局部地区压力小于0的情形，这说明参考点并不位于压力最低的地方，对于压差的计算毫无影响。”
  压力相对值的设定也可能会影响收敛的效率，相关讨论可以参考文献⁶
- residualControl子字典
  在residualControl子字典里，可以设置各个场在稳态计算时的收敛判断误差，当模拟时两次迭代步之间的误差小于residualControl中的值时，模拟将停止。该子字典并不是必须要设置的，如果空缺，SIMPLE算法会按照controlDict文件里的最大迭代次数进行模拟。
relaxationFactors字典
relaxationFactor字典用于设置亚松弛因子，设置的方法有两种，一种是对方程进行亚松弛，一种是对场进行亚松弛。对方程进行亚松弛是指在方程矩阵系统建立后，求解前对矩阵系统进行亚松弛，因为这种松弛是在方程求解前，因此又称为隐式亚松弛。对场进行亚松弛是指在方程求解后对结果直接进行亚松弛，因为这种松弛是在方程求解后，因此又称为显式亚松弛。
观察simpleFoam的代码可以发现，对于速度方程，其亚松弛代码为UEqn.relax()，且该代码位于速度方程求解前，显然，这是一种隐式亚松弛。而对于压力场，其亚松弛代码为p.relax()，且其位置位于压力方程求解后，显然，这是一种显式亚松弛。关于显式亚松弛与隐式亚松弛，陶文铨院士在其著作中也有相关论述。⁷

2.3 PISO算法

2.3.1标准PISO算法

PISO 算法⁸最初被用来处理瞬态问题，其方程的构建过程与SIMPLE算法基本一致:

首先求解动量预测方程(2.13)得到预测速度 $\vec{U^r}$ ，根据 $\vec{U^r}$ 构建 $\vec{HbyA}$ 后带入压力泊松方程(2.14)求出压力，再根据压力和式(2.15)求解出新的速度。若按SIMPLE系列算法，此时应该将新的压力带回动量预测方程进行下一次迭代，但PISO算法并不这样做，PISO算法在求解完一次新的压力和速度后选择将求解得到的新速度带回压力泊松方程再次求解，然后再次求得一个新的压力，继而再次更新速度，压力泊松方程(2.14)与速度更新方程(2.15)之间的这种循环成为压力修正。PISO算法的框图如下：

图2.2 PISO算法框图

需要指出的是，PISO算法也有用于稳态计算的版本，但鉴于PISO算法在OpenFOAM中仅用作瞬态计算，在此不予赘述，感兴趣的读者可以参考相关文献⁹。

2.3.2 OpenFOAM中的PISO算法

之前已经对simpleFoam的代码进行过较为详细的解释，icoFoam中代码与simpleFoam中代码多有重叠，因此我们只选择较为重要的部分进行解释。

代码2 pisoFoam代码解读

 #include "fvCFD.H"
 #include "pisoControl.H"
 
 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
 
 int main(int argc, char *argv[])
 {
     #include "setRootCaseLists.H"
     #include "createTime.H"
     #include "createMesh.H"
 
     pisoControl piso(mesh);
 
     #include "createFields.H"
     #include "initContinuityErrs.H"
 
     // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
 
     Info<< "\nStarting time loop\n" << endl;
 
     while (runTime.loop())
     {
         Info<< "Time = " << runTime.timeName() << nl << endl;
 
         #include "CourantNo.H"
 
         // Momentum predictor
         //译：动量预测方程
 
         fvVectorMatrix UEqn
         (
             fvm::ddt(U)
           + fvm::div(phi, U)
           - fvm::laplacian(nu, U)
         );
 
         if (piso.momentumPredictor())
         {
             solve(UEqn == -fvc::grad(p));
         }
         //释：构建并求解动量预测方程
 
         // --- PISO loop
         //译：PISO循环
         while (piso.correct())
         {
             volScalarField rAU(1.0/UEqn.A());
             volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p));
             surfaceScalarField phiHbyA
             (
                 "phiHbyA",
                 fvc::flux(HbyA)
               + fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)
             );
            //释：组建HbyA
             adjustPhi(phiHbyA, U, p);
    
             // Update the pressure BCs to ensure flux consistency
             //译：更新压力边界条件以保证通量守恒
             constrainPressure(p, U, phiHbyA, rAU);
 
             // Non-orthogonal pressure corrector loop
             //译：非正交压力修正循环
             while (piso.correctNonOrthogonal())
             {
                 // Pressure corrector
                 //译：压力修正
 
                 fvScalarMatrix pEqn
                 (
                     fvm::laplacian(rAU, p) == fvc::div(phiHbyA)
                 );
 
                 pEqn.setReference(pRefCell, pRefValue);
 
                 pEqn.solve();
                //释：组建并求解压力方程
                 if (piso.finalNonOrthogonalIter())
                 {
                     phi = phiHbyA - pEqn.flux();
                 }
                 //释：在最后一次求解压力泊松方程时更新通量
             }
 
             #include "continuityErrs.H"
 
             U = HbyA - rAU*fvc::grad(p);
             //释：更新速度
             U.correctBoundaryConditions();
         }
 
         runTime.write();
 
         Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << " s"
             << "  ClockTime = " << runTime.elapsedClockTime() << " s"
             << nl << endl;
     }
 
     Info<< "End\n" << endl;
 
     return 0;
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102

OpenFOAM中还有另一个使用PISO算法的单相不可压缩求解器pisoFoam。pisoFoam是icoFoam的升级版本，支持了湍流模型，旋转坐标系等功能。通常情况下如果需要使用PISO算法计算不可压缩流体的瞬态运动，推荐使用pisoFoam进行模拟，icoFoam更像是一个为了解释算法而设计的求解器。

PISO算法的设置位于fvSolutions字典中的PISO子子字典中，其需要设置的项主要有：

momentumPredictor：是否进行动量预测，在PISO算法中，动量预测并不是必须的，进行动量预测可以增加计算的稳健性，但会带来一定的计算资源消耗，不过这种消耗往往是可以忽略的。
nCorrectors：设置压力修正循环的次数，可以增加压力修正次数以获得更高的计算稳定性。一般推荐设置为2-3次。
nNonOrthogonalCorrectors：设置非正交循环次数，可以参考SIMPLE算法中的设置。在一个压力修正循环内部，压力泊松方程求解次数=非正交循环次数+1

pisoFoam可以对速度方程进行亚松弛（icoFoam无相应代码）而无对压力场进行亚松弛的选项。瞬态PISO算法的亚松弛不是必须的。

系列说明：
接触有限体积法有一段时间了，也看了一些资料，但是有时候总觉得看过一遍之后什么也记不住。老话说得好，眼过千遍不如手过一遍，久而久之我就有了写一些比较像样子的笔记的想法。初学的时候曾经写过一本叫“OpenFOAM编程笔记：单相不可压缩流动”的册子，但当时基础太差（现在基础也不好），错误太多，倒不如推倒重来。
本系列将持续更新，欢迎各位挑错交流，挑错交流可以直接留言也可以联系邮箱cloudbird7@foxmail.com。等到预定内容全部写完后我将集结所有内容为一个独立的文件，开放下载。

Patankar S V , Spalding D B . A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows[J]. Journal of Heat Mass Transfer, 1972, 15(10):1787-1806. ↩︎
Van Doormaal J P , Raithby G D . Enhancements of the simple method for predicting incompressible fluid flows[J]. Numerical Heat Transfer Applications, 1984, 7(2):147-163. ↩︎
Versteeg H K , Malalasekera W . An Introduction to Computational Fluid Dynamic: The Finite Volume Method Second edition [M]. Edinburgh Gate：Pearson Education, 2007. 191-192. ↩︎
Versteeg H K , Malalasekera W . An Introduction to Computational Fluid Dynamic: The Finite Volume Method Second edition [M]. Edinburgh Gate：Pearson Education, 2007. 262. ↩︎
李东岳.simpleFoam解析.[EB/OL]. http://www.dyfluid.com/docs/energy.html, 20200614/20200718 ↩︎
陶文铨. 数值传热学[M]. 西安交通大学出版社, 2001.213 ↩︎
陶文铨. 数值传热学[M]. 西安交通大学出版社, 2001.214 ↩︎
Issa R I . Solution of the implicitly discretised fluid flow equations by operator-splitting[J]. Journal of Computational Physics, 1991, 62(1):40-65. ↩︎
Versteeg H K , Malalasekera W . An Introduction to Computational Fluid Dynamic: The Finite Volume Method Second edition [M]. Edinburgh Gate：Pearson Education, 2007. 193-196. ↩︎

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/AllinToyou/article/detail/529340