转载请注明出处：http://www.cnblogs.com/ymingjingr/p/4271742.html
目录
机器学习基石笔记1——在何时可以使用机器学习(1)
机器学习基石笔记2——在何时可以使用机器学习(2)
机器学习基石笔记3——在何时可以使用机器学习(3)(修改版)
机器学习基石笔记4——在何时可以使用机器学习（4）
机器学习基石笔记5——为什么机器可以学习（1）
机器学习基石笔记6——为什么机器可以学习（2）
机器学习基石笔记7——为什么机器可以学习（3）
机器学习基石笔记8——为什么机器可以学习（4）
机器学习基石笔记9——机器可以怎样学习（1）
机器学习基石笔记10——机器可以怎样学习（2）
机器学习基石笔记11——机器可以怎样学习（3）
机器学习基石笔记12——机器可以怎样学习（4）
机器学习基石笔记13——机器可以怎样学得更好（1）
机器学习基石笔记14——机器可以怎样学得更好（2）
机器学习基石笔记15——机器可以怎样学得更好（3）
机器学习基石笔记16——机器可以怎样学得更好（4）
十、Logistic Regression
罗杰斯特回归（最常见到的翻译：Logistic回归）。
10.1 Logistic Regression Problem
Logistic回归问题。
使用二元分类分析心脏病复发问题，其输出空间只含有两项{+1，-1}，分别表示复发和不发复发。在含有噪音的情况下，目标函数f可以使用目标分布P来表示，如公式10-1所示，此情形的机器学习流程图如图10-1所示。
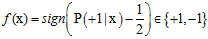（公式10-1）
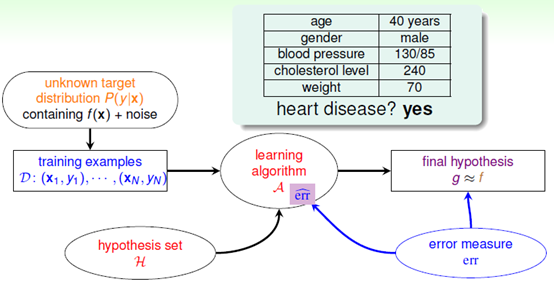
图10-1 心脏病复发二元分类流程图
但是通常情况下，不会确定的告知患者，心脏病一定会复发或者一定不会，而是以概率的方式告知患者复发的可能性，如图10-2所示，一位患者心脏病复发的可能性为80%。
图10-2 以概率的形式表示复发可能性
此种情况被称为软二元分类（soft binary classification），目标函数f的表达如公式10-2所示，其输出以概率的形式，因此在0~1之间。
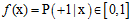（公式10-2）
面对如公式10-2的目标函数，理想的数据集D（输入加输出空间）应如图10-3所示。
图10-3 理想的数据集D
所有的输出都以概率的形式存在，如
，用心脏病复发的例子来说明，一般病人只有心脏病发与没复发两种情况，而不可能在病历中记录他曾经的病发概率，现实中的训练数据应如图10-4所示。
图10-4 实际训练数据
可以将实际训练数据看做含有噪音的理想训练数据。
问题是如何使用这些实际的训练数据以解决软二元分类的问题，即假设函数如何设计。
首先回忆在之前的几章内容中提到的两种假设函数（二元分类和线性回归）中都具有的是哪部分？
答案是求输入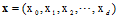
各属性的加权总分数（score），（还记得第二章中用成绩分数来说明加权求和的意义吗？）可以使用公式10-3表示。
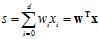（公式10-3）
如何把该得分从在整个实数范围内转换成为一个0~1之间的值呢？此处就引出了本章的主题，logistic函数（logistic function）用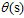
表示。分数s越大风险越高，分数s越小风险越低。假设函数h如公式10-4所示，函数曲线的示意图如图10-5所示。
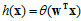（公式10-4）
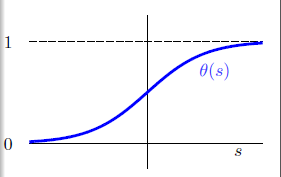
图10-5 logistic函数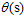
的示意图
具体的logistic函数的数学表达式如公式10-5所示。
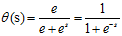（公式10-5）
代入几个特殊的数值检验是否能将整个实数集上的得分映射到0~1之间，代入负无穷，得
；代入0，得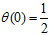
；代入正无穷，得
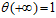。logistic函数
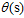完美的将整个实数集上的值映射到了0~1区间上。
观察函数的图形，该函数是一个平滑（处处可微分），单调（monotonic）的S形（sigmoid）函数，因此又被称为sigmoid函数。
通过logistic函数的数学表达式，重写软二元分类的假设函数表达，如公式10-6所示。
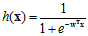（公式10-6）
10.2 Logistic Regression Error
Logistic回归错误。
将logisitic回归与之前学习的二元分类和线性回归做一对比，如图10-7所示。
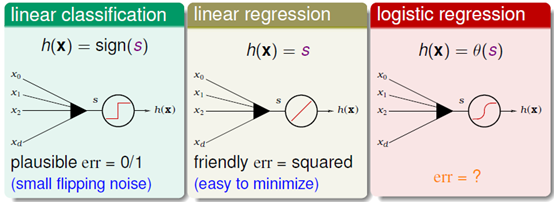
图10-7 二元分类、线性回归与logistic回归的对比
其中分数s是在每个假设函数中都会出现的
，前两个学习模型的错误衡量分别对应着0/1错误和平方错误，而logistic回归所使用的err函数应如何表示则是本节要介绍的内容。
从logistic回归的目标函数可以推导出公式10-7成立。
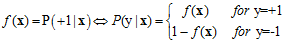（公式10-7）
其中花括号上半部分不难理解，是将目标函数等式左右对调的结果，而下半部分的推导也很简单，因为+1与-1的几率相加需要等于1。
假设存在一个数据集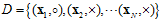
,则通过目标函数产生此种数据集样本的概率可以用公式10-8表示。
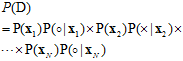(公式 10-8)
就是各输入样本产生对应输出标记概率的连乘。而从公式10-7可知公式10-8可以写成公式10-9的形式。
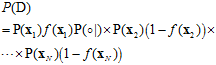（公式10-9）
但是函数f是未知的，已知的只有假设函数h，可不可以将假设函数h取代公式10-9中的f呢？如果这样做意味着什么？意味着假设函数h产生同样数据集样本D的可能性多大，在数学上又翻译成似然（likelihood），替代之后的公式如公式10-10所示。
（公式10-10）
假设假设函数h和未知函数f很接近（即err很小），那么h产生数据样本D的可能性或叫似然（likelihood）和f产生同样数据D的可能性（probability）也很接近。函数f既然产生了数据样本D，那么可以认为函数f产生该数据样本D的可能性很大。因此可以推断出最好的假设函数g，应该是似然最大的假设函数h，用公式10-11表示。
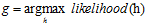（公式10-11）
在当假设函数h使用公式10-6的logistic函数，可以得到如公式10-12的特殊性质。
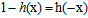（公式10-12）
因此公式10-10可以写成公式10-13。
此处注意，计算最大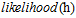的
时，所有的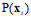
对大小没有影响，因为所有的假设函数都会乘以同样的
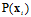，即h的似然只与函数h对每个样本的连乘有关，如公式10-14。
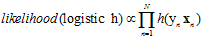(公式10-14)
其中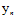
表示标记，将标记代替正负号放进假设函数中使得整个式子更加简洁。寻找的是似然最大的假设函数h，因此可以将公式10-14代入寻找最大似然的公式中，并通过一连串的转换得到公式10-15。
（假设函数h与加权向量w一一对应）
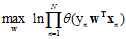
（连乘公式不容易求解最大问题，因此求其对数，此处以自然对数e为底）
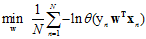
（之前都是在求最小问题，因此将最大问题加上一个负号转成了最小问题，为了与以前的错误衡量类似，多成了一个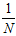
。）
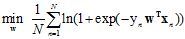
（将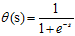
代入表达式得出上述结果）
（公式10-15）
公式10-15中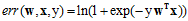
，这个错误函数称作交叉熵错误（cross-entropy error）。
10.3 Gradient of Logistic Regression Error
Logistic回归错误的梯度。
推导出logistic回归的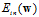
，下一步的工作是寻找使得
最小的权值向量w。
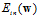的表达如公式10-16所示。
（公式10-16）
仔细的观察该公式，可以得出该函数为连续（continuous）可微（differentiable）的凸函数，因此其最小值在梯度为零时取得，即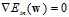
。那如何求解
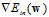呢？即为对权值向量w的各个分量求偏微分，对这种复杂公式求解偏微分可以使用微分中的连锁律。将公式10-16中复杂的表示方式用临时符号表示，为了强调符号的临时性，不使用字母表示，而是使用
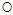和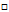
，具体如公式10-17。
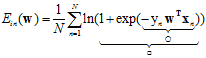（公式10-17）
对权值向量w的单个分量求偏微分过程如公式10-18所示。
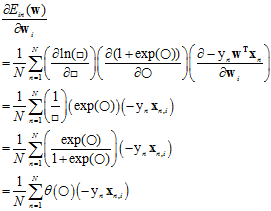（公式10-18）
其中
函数为10.1节中介绍的logistic函数。而求梯度的公式可以写成公式10-19所示。
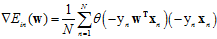（公式10-19）
求出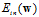
的梯度后，由于
为凸函数，令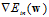
为零求出的权值向量w，即使函数
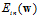取得最小的w。
观察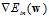
，发现该函数是一个
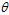函数作为权值，关于
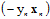的加权求和函数。
假设一种特殊情况，函数的所有权值为零，即所有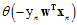
都为零，可以得出
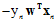趋于负无穷，即
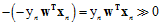，也意味着所有的
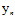都与对应的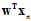
同号，即线性可分。
排除这种特殊情况，当加权求和为零时，求该问题的解不能使用类似求解线性回归时使用的闭式解的求解方式，此最小值又该如何计算？
还记得最早使用的PLA的求解方式吗？迭代求解，可以将PLA的求解步骤合并成如公式10-20的形式。
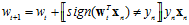（公式10-20）
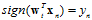时，向量不变；
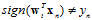时，加上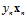
。将使用一些符号将该公式更一般化的表示，如公式10-21所示。
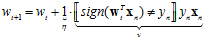（公式10-21）
其中多乘以一个1，用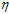
表示，表示更新的步长，PLA中更新的部分用v来代表，表示更新的方向。而这类算法被称为迭代优化方法（iterative optimization approach）。
10.4 Gradient Descent
梯度下降。
Logistic回归求解最小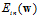
也使用上节中提到的迭代优化方法，通过一步一步改变权值向量
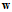，寻找使得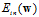
最小的变权值向量
，迭代优化方法的更新公式如公式10-22所示。
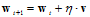（公式10-22）
针对logistic回归个问题，如何设计该公式中的参数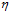
和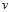
是本节主要解决的问题。
回忆PLA，其中参数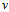 
来自于修正错误，观察logistic回归的
，针对其特性，设计一种能够快速寻找最佳权值向量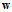
的方法。
如图10-8为logistic回归的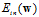
关于权值向量w的示意图为一个平滑可微的凸函数，其中图像谷底的点对应着最佳w，使得
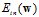最小。如何选择参数
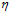和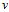
可以使得更新公式快速到达该点？
图10-8 logistic回归的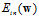
示意图
为了分工明确，设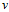
作为单位向量仅代表方向，
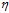代表步长表示每次更新改变的大小。在
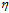固定的情况下，如何选择
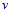的方向保证更新速度最快？是按照
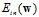最陡峭的方向更改。即在
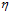固定，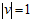
的情况下，最快的速度（有指导方向）找出使得
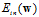最小的w，如公式10-23所示。
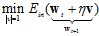（公式10-23）
以上是非线性带约束的公式，寻找最小w仍然非常困难，考虑将其转换成一个近似的公式，通过寻找近似公式中最小w，达到寻找原公式最小w的目的，此处使用到泰勒展开（Taylor expansion），回忆一维空间下的泰勒公式，如公式10-24所示。
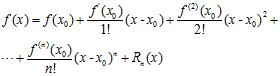(公式10-24)
同理，在
很小时，将公式10-23写成多维泰勒展开的形式，如公式10-25所示。
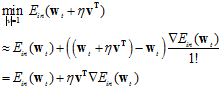（公式10-25）
其中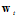
相当于公式10-24中的
，
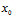相当于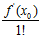
。通俗点解释，将原
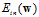的曲线的形式看做一小段一小段的线段的形式，即
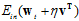的曲线可以看做
周围一段很小的线段。
因此求解公式10-26最小情况下的w，可以认为是近似的求解公式10-23最小状况下的w。
（公式10-26）
该公式中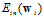
是已知值，而
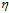为给定的大于零的值，因此求公式10-26最小的问题又可转换为求公式10-27最小的问题。
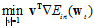（公式10-27）
两个向量最小的情况为其方向相反，即乘积为负值，又因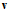
是单位向量，因此方向
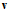如公式10-28所示。
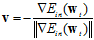（公式10-27）
在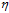
很小的情况下，将公式10-27代入公式10-22得公式10-28，具体的更新公式。
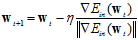（公式10-27）
该更新公式表示权值向量w每次向着梯度的反方向移动一小步，按照此种方式更新可以尽快速度找到使得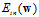
最小的w。此种方式称作梯度下降（gradient descent），简写为GD，该方法是一种常用且简单的方法。
讲完了参数v的选择，再回头观察事先给定的参数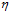
的取值对梯度下降的影响，如图10-9所示。
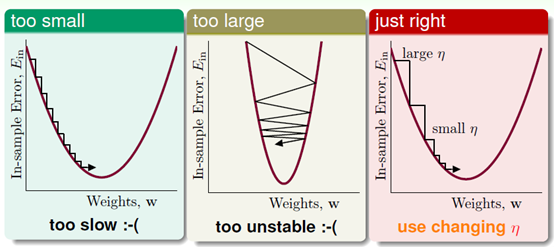
图10-9参数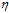
的大小对梯度下降的影响
如图10-9最左，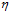
太小时下降速度很慢，因此寻找最优w的速度很慢；图10-9中间，当
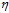太大时，下降不稳定，甚至可能出现越下降越高的情况；合适的
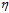应为随着梯度的减小而减小，如图最右所示，即参数
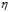是可变的，且与梯度大小
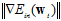成正比。
根据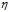
与梯度大小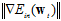
成正比的条件，可以将
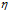重新给定，新的
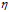如公式10-28所示。
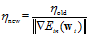（公式10-28）
最终公式10-27可写成公式10-29。
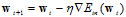（公式10-29）
此时的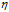
被称作固定的学习速率（fixed learning rate），公式10-29即固定学习速率下的梯度下降。
Logistic回归算法的步骤如下：
设置权值向量w初始值为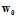
，设迭代次数为t，
；
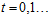计算梯度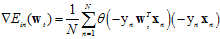
;
对权值向量w进行更新，
；
直到
或者迭代次数足够多。
