16种常用智能优化算法改进策略---剩余篇，可用于改进所有智能算法，让小白也会改进智能算法。..._自适应变异与交叉策略以及种群寻优更新策略

俗话说，授人以鱼不如授人以渔。

智能算法的改进作为一个创新点，大家任何时候都可以拿来去水水论文，甚至专利。

网上关于智能算法改进的论文不计其数！但是，如果细数改进策略！也是能够数的过来的！

之前作者推出过两篇关于智能算法常用的改进策略。包含的改进策略有：

①莱维飞行，②随机游走，③螺旋飞行，④高斯随机游走，⑤三角形游走，⑥高斯变异，⑦t分布扰动变异，⑧自适应t分布扰动变异，⑨柯西变异，⑩差分变异。

为了方便大家对于策略代码编写的学习和移植，作者将这十余种策略全部用于经典的粒子群算法。

因此只要你理解了经典的粒子群算法，再与改进的粒子群算法进行对比，那么你就能马上理解这些策略是如何运用于智能优化算法的。举一反三，大家自然而然也就会改进其他算法了！

现附上之前推出的十种改进策略，链接如下：

常用智能优化算法改进策略---飞行游走篇（五种策略）可用于改进所有智能算法，让小白也会改进智能算法。

常用智能优化算法改进策略---变异篇（五种变异策略）可用于改进所有智能算法，让小白也会改进智能算法。

除了以上10种改进策略，本期作者将再推出6种常见的改进策略。

这6种改进策略分别是：

①纵横交叉，②透镜成像反向学习，③动态反向学习，④正余弦，⑤黄金正弦，⑥自适应收敛因子

算上上面的10种，加起来一共是16种智能算法改进策略。

学会这16种策略，当你再去查阅改进智能算法的相关文献，你就会惊奇的发现，很多文献的策略都逃不过这16种。

下面一一介绍今天新推出的6种改进策略！

为了方便大家对这最新的6种改进策略深入了解，作者同样将这6种策略用在简单易懂的粒子群算法中，以此来教大家如何运用这6种策略，今后也方便大家移植到别的智能算法中。

①纵横交叉

网上找到一篇文献，关于纵横交叉策略的介绍，写的还很不错。

关于纵横交叉策略，作者想说的是，这个策略基本上对所有的智能算法都可以适用，而且，加入后都会有很大的改进效果，但缺陷就是，加入这个纵横交叉策略之后，会增加智能算法的复杂度。所以说，万物都讲究一个平衡制约，阴阳调衡哈！

如果说，你的实际工程案例的适应度函数模型比较简单，那么就可以尝试该策略，会有不错的效果。但是如果说，你的实际工程案例模型迭代一次都需要很长时间，那么就建议不要用该策略了，因为当程序跑完的时候，你也差不多该毕业了。

参考文献：梁昔明,张洋,龙文.含有纵横交叉策略的蜘蛛猴优化算法[J].数学的实践与认识,2022,52(12):144-158.

②透镜成像反向学习(反向学习)

反向学习策略，作为智能算法常用的改进策略，在很多改进智能算法的文献都能找到他的影子！

透镜成像反向学习主要的思想是以当前坐标为基准通过凸透镜成像的原理生成一个反向位置来扩大搜索范围，这样可以既能跳出当前位置，又可以扩大搜索范围，提高了种群的多样性。

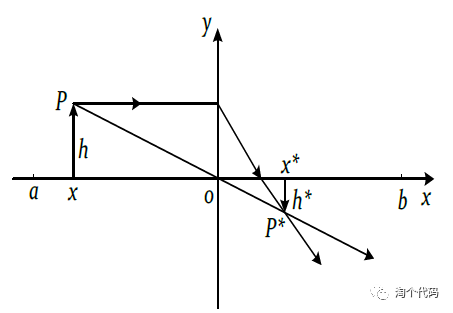
透镜成像反向学习策略示意图

基于透镜成像原理的反向学习公式如下：

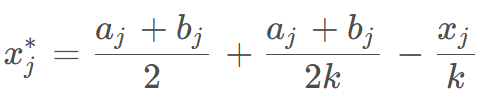
a,b就是解的上下限，当k=1时候，该公式就是标准的反向学习。

由上述可知，反向学习就是特殊的透镜成像反向学习，采用反向学习得到的是固定的反向解。而通过调整k 的大小，可以在透镜反向学习中获得动态变化的反向解，进一步提升算法的寻优能力。

参考文献：Di Wu, Honghua Rao, Changsheng Wen, et al. Modified Sand Cat Swarm Optimization Algorithm for SolvingConstrained Engineering Optimization Problems[J]. Mathematics. 2022, 10(22), 4350.

③动态反向学习

所谓动态反向学习，就在于a,b取值的巧妙，这里的a,b不再是初始化的时候给出的上下限，而是取每次迭代过程中，所有粒子位置每一维度的上下限。

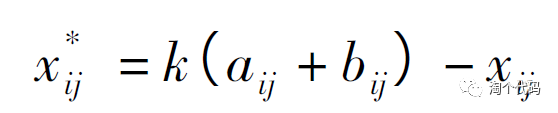
式中，aij = min(xij( t) ) ，bij = max(xij( t) ) ，分别为当前搜索空间的最小值和最大值，其随迭代次数的改变而变化。k为反向系数。

参考文献：陈娟,赵嘉,肖人彬等.基于动态反向学习和莱维飞行的双搜索模式萤火虫算法[J].信息与控制,2023,52(05):607-615.DOI:10.13976/j.cnki.xk.2023.2352.

④正余弦策略

大家在查阅很多很多改进的智能算法中，经常会见到融合正余弦的影子，这里也说一下正余弦策略（sinecosine algorithm，SCA）。通过利用正余弦模型震荡变化特性对粒子位置进行作用，维持粒子个体多样性，进而提高智能算法的全局搜索能力。SCA的中心思想是根据正余弦模型的振荡变化对整体和局部寻优，获取整体最优值。公式如下：

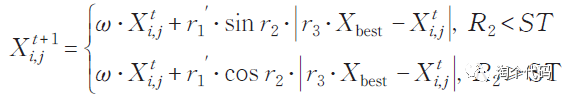
参考文献：李爱莲,全凌翔,崔桂梅等.融合正余弦和柯西变异的麻雀搜索算法[J].计算机工程与应用,2022,58(03):91-99.

⑤融合黄金正弦

黄金正弦也是一种常用的改进策略。可以看到目前有很多人融合该算法改进智能算法。

Golden-SA 不是模拟自然现象设计的，而是利用数学中的正弦函数进行计算迭代寻优，并在位置更新过程中引入黄金分割数使“搜索”和“开发”达到良好的平衡。公式如下：

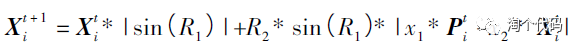
参考文献：肖子雅,刘升.精英反向黄金正弦鲸鱼算法及其工程优化研究[J].电子学报,2019,47(10):2177-2186.

⑥自适应收敛因子

这一个改进策略其实非常常见，也非常实用！在很多改进的算法里边都能看到。但是想要用好这一策略，需要大家不断的进行尝试。因为它会影响算法在不同阶段的收敛速度。

当然，这一阶段的公式，也是非常之丰富！但一般就是指数与非线性函数的组合。然后从一个数字增长或者降低到另一个数字。

比如：

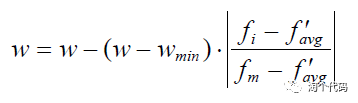
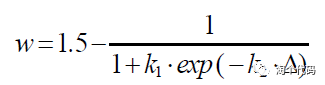
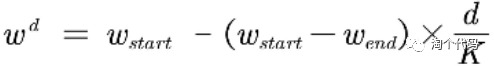
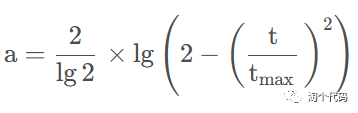
类似这样的公式还有很多很多，这一点改进一般也是最简单的，大家在今后的学习中自行探索即可！这里的参考文献太多了，就不放了哈！

结果展示

在CEC2005函数集进行展示，设置迭代次数1000次，种群个数100个。

其中PSO为原始粒子群，WPSO为自适应收敛因子策略，Goldensine为黄金正弦策略，Reverselearn为透镜成像反向学习策略，DynamicReverselearn为动态反向学习策略，Sincos为正余弦策略，Crisscrossing为纵横交叉策略。

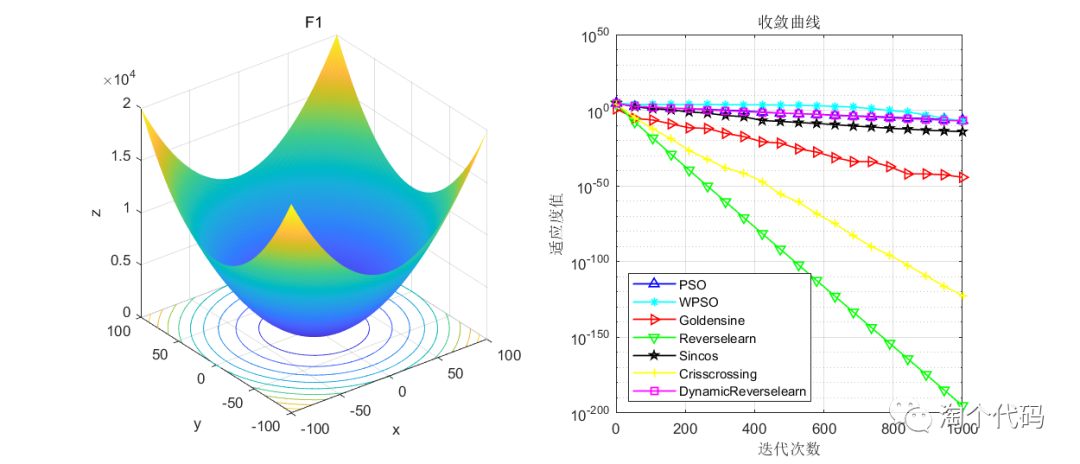
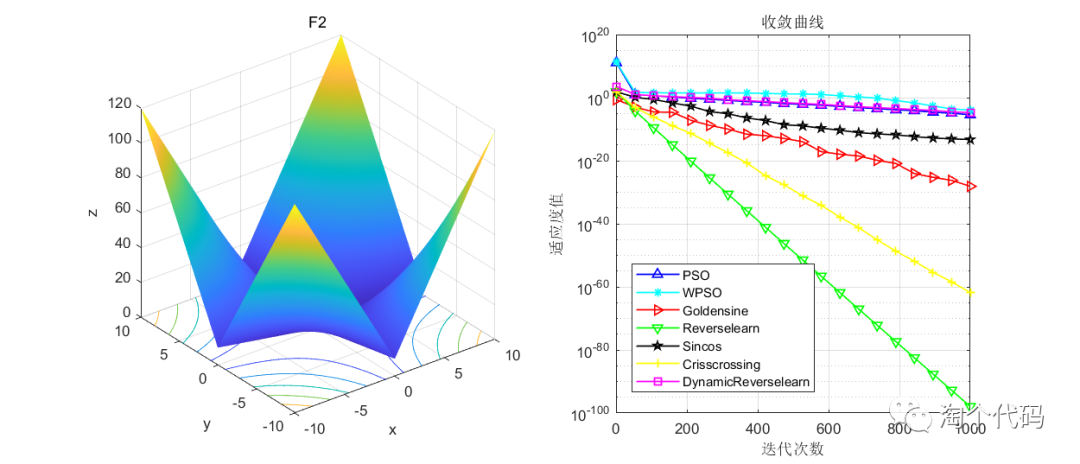
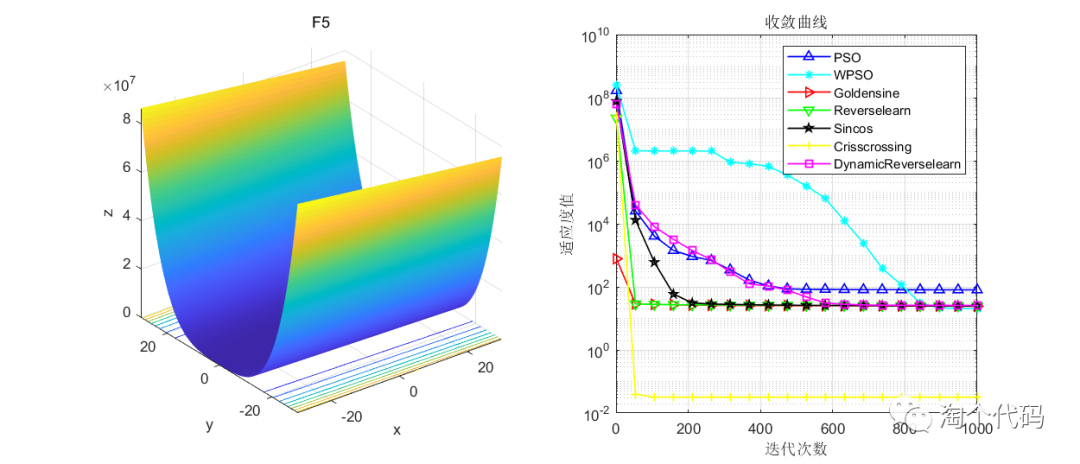
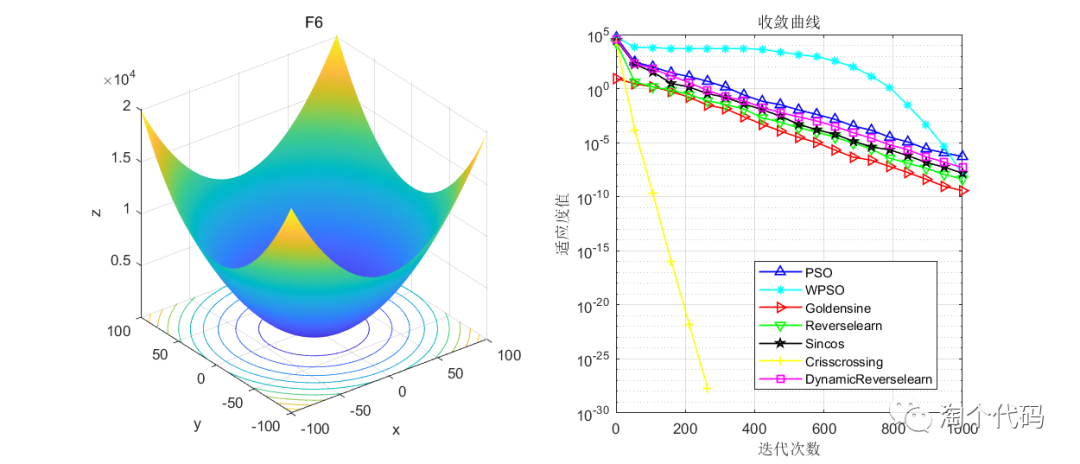
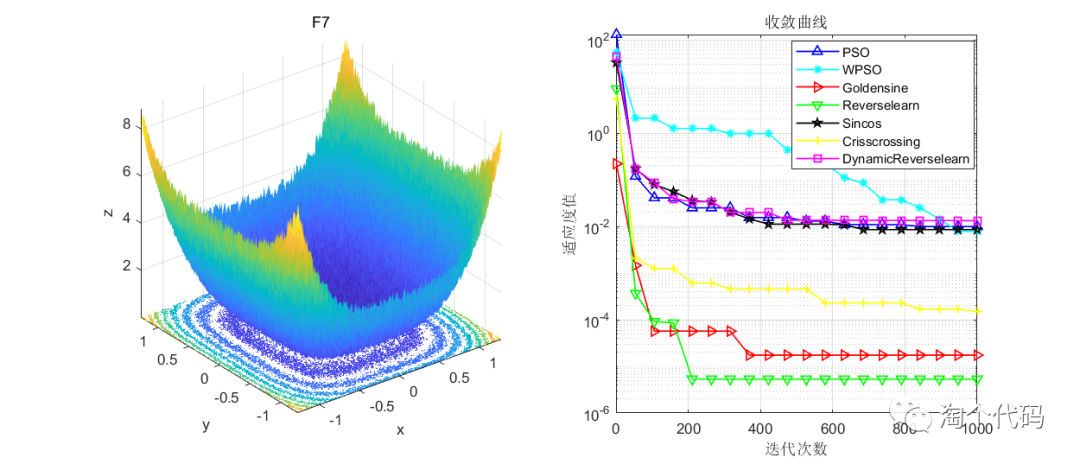
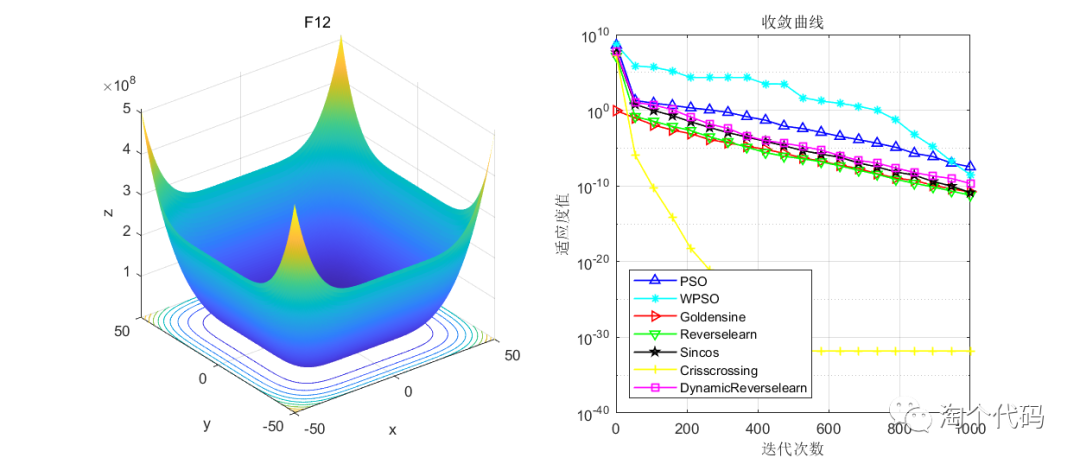
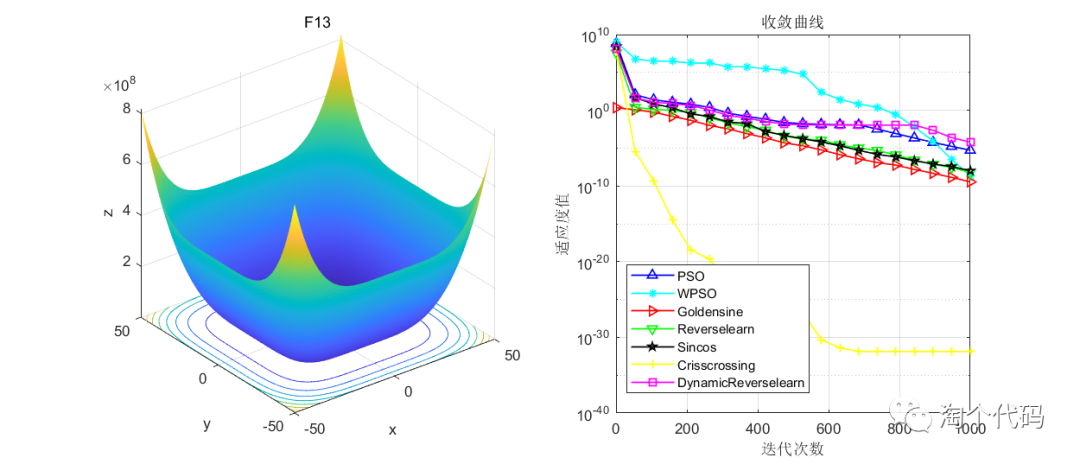
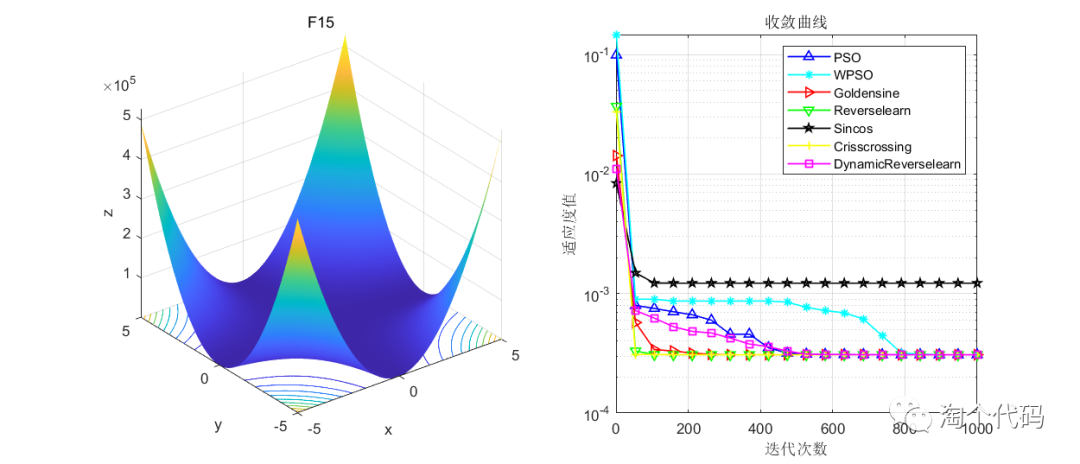
注意！本程序代码只是为了教大家如何使用这几种变异策略，如果看到改进后的算法没有原始算法效果好，请不要见怪！

但是可以看到的是，除了自适应收敛因子策略在一些函数表现不佳以外（也可能是作者加的这个公式不太好），其他的策略都比原始的粒子群算法要好。

友情提示：策略算法是给出了，但不是说只要你加入了策略，算法性能就一定能提升，关键还是要看这些策略的作用分别是什么，是帮助算法跳出最优解？是扩展搜索范围增强全局寻优能力？是加速算法收敛？只有明确了策略的功能和自己要改进算法的弊端，有效结合，才能提升自己的算法性能。要分析其原理并不断进行尝试！

代码展示

%%
clear
clc
close all
number='F15'; %选定优化函数，自行替换:F1~F23
[lb,ub,dim,fobj]=CEC2005(number);  % [lb,ub,D,y]：下界、上界、维度、目标函数表达式
SearchAgents=100;                      % population members 
Max_iterations=1000;                  % maximum number of iteration
 
 
%% 调用PSO算法
[fMin , bestX, PSO_Convergence_curve ] = PSO(SearchAgents, Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by PSO  for ' [num2str(number)],'  is : ', num2str(fMin)]);
fprintf ('Best solution obtained by PSO: %s\n', num2str(bestX,'%e  '));
 
 
%% 调用自适应权重因子的PSO
[Best_score,Best_pos,WPSO_curve]=WPSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);  % Calculating the solution of the given problem using WPSO
display(['The best optimal value of the objective funciton found by WPSO  for ' [num2str(number)],'  is : ', num2str(Best_score)]);
fprintf ('Best solution obtained by WPSO: %s\n', num2str(Best_pos,'%e  '));
 
 
%% 调用黄金正弦的PSO算法
[Alpha_score,Alpha_pos,Golden_sine_PSO_Convergence_curve]=Golden_sine_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by Golden_sine_PSO  for ' [num2str(number)],'  is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by Golden_sine_PSO: %s\n', num2str(Alpha_pos,'%e  '));
%% 调用正余弦的PSO算法
[Alpha_score,Alpha_pos,Sin_cos_PSO_Convergence_curve]=Sin_cos_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by Sin_cos_PSO  for ' [num2str(number)],'  is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by Sin_cos_PSO: %s\n', num2str(Alpha_pos,'%e  '));
%% 调用透镜成像反向学习的PSO算法
[Alpha_score,Alpha_pos,Reverse_learn_PSO_Convergence_curve]=Reverse_learn_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by Reverse_learn_PSO  for ' [num2str(number)],'  is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by Reverse_learn_PSO: %s\n', num2str(Alpha_pos,'%e  '));
%% 调用纵横交叉的PSO算法
[Alpha_score,Alpha_pos,Crisscrossing_PSO_Convergence_curve]=Crisscrossing_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by Crisscrossing_PSO  for ' [num2str(number)],'  is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by Crisscrossing_PSO: %s\n', num2str(Alpha_pos,'%e  '));
%% 调用动态反向学习的PSO算法
[Alpha_score,Alpha_pos,Dynamic_Reverse_learn_PSO_Convergence_curve]=Dynamic_Reverse_learn_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by Dynamic_Reverse_learn_PSO  for ' [num2str(number)],'  is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by Dynamic_Reverse_learn_PSO: %s\n', num2str(Alpha_pos,'%e  '));
 %% Figure
figure1 = figure('Color',[1 1 1]);
G1=subplot(1,2,1,'Parent',figure1);
func_plot(number)
title(number)
xlabel('x')
ylabel('y')
zlabel('z')
subplot(1,2,2)
G2=subplot(1,2,2,'Parent',figure1);
CNT=20;
k=round(linspace(1,Max_iterations,CNT)); %随机选CNT个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:Max_iterations;
if ~strcmp(number,'F16')&&~strcmp(number,'F9')&&~strcmp(number,'F11')  %这里是因为这几个函数收敛太快，不适用于semilogy，直接plot
    semilogy(iter(k),PSO_Convergence_curve(k),'b-^','linewidth',1);
    hold on
    semilogy(iter(k),WPSO_curve(k),'c-*','linewidth',1);
    hold on
    semilogy(iter(k),Golden_sine_PSO_Convergence_curve(k),'r->','linewidth',1);
    hold on
    semilogy(iter(k),Reverse_learn_PSO_Convergence_curve(k),'g-v','linewidth',1);
    hold on
    semilogy(iter(k),Sin_cos_PSO_Convergence_curve(k),'k-p','linewidth',1);
    hold on
    semilogy(iter(k),Crisscrossing_PSO_Convergence_curve(k),'y-+','linewidth',1);
    hold on
    semilogy(iter(k),Dynamic_Reverse_learn_PSO_Convergence_curve(k),'m-s','linewidth',1);
    
else
    plot(iter(k),PSO_Convergence_curve(k),'b-^','linewidth',1);
    hold on
    plot(iter(k),WPSO_curve(k),'c-*','linewidth',1);
    hold on
    plot(iter(k),Golden_sine_PSO_Convergence_curve(k),'r->','linewidth',1);
    hold on
    
    plot(iter(k),Reverse_learn_PSO_Convergence_curve(k),'g-v','linewidth',1);
    hold on
    plot(iter(k),Sin_cos_PSO_Convergence_curve(k),'k-p','linewidth',1);
   
    hold on
    plot(iter(k),Crisscrossing_PSO_Convergence_curve(k),'y-+','linewidth',1);
    hold on
    plot(iter(k),Dynamic_Reverse_learn_PSO_Convergence_curve(k),'m-s','linewidth',1);
end
grid on;
title('收敛曲线')
xlabel('迭代次数');
ylabel('适应度值');
box on
legend('PSO','WPSO','Goldensine','Reverselearn','Sincos','Crisscrossing','DynamicReverselearn')
set (gcf,'position', [300,300,1000,430])

代码目录

直接运行MAIN.m脚本文件即可！

代码获取

关注下方小卡片，获取更多代码