Fast-Planner论文第一篇：Robust and Efficient Quadrotor Trajectory Generation for Fast Autonomous Flight_fast planner论文

摘要：

采用运动动力学路径搜索方法在离散化控制空间中寻找安全、运动可行、最短时间的初始轨迹。利用b样条的凸包特性，结合欧几里得距离场(EDF)的梯度信息和动态约束，采用b样条优化方法提高轨迹的平滑度和间隙。最后，通过将最终轨迹表示为非均匀b样条，采用迭代时间调整方法保证轨迹的动态可行和开放性。

引言

在四旋翼运动规划领域存在两个重要的未被解决的问题：1、有限的时间和板载计算资源下，现有工作不能保证高成功率地生成安全和运动动力学可行的轨迹；2、为保证运动动力学可行性，对速度和加速度进行了较大限制。
在本文中，我们提出了一种完整且鲁棒的在线轨迹生成方法来系统地解决这两个问题。采用了基于启发式搜索和线性二次最小时间控制的运动路径搜索方法。该算法在离散化控制空间中高效地搜索安全、可行且时间最短的初始路径。然后通过精心设计的b样条优化来优化初始路径，该优化利用b样条的凸包特性来结合梯度信息和动态约束。该算法改进了初始路径，快速收敛到平滑、安全、动态可行的轨迹。最后，将轨迹表示为非均匀b样条，研究了导数控制点与时间分配的关系。在此基础上，采用迭代时间调整的方法将不可行的速度和加速度剔除，同时避免了对它们的保守约束。

运动动力学路径搜索

前端运动动力学路径搜索模块来源于为自动驾驶提出的混合状态A算法。它在体素网格地图中搜索一条相对于持续时间和控制成本最小的轨迹。

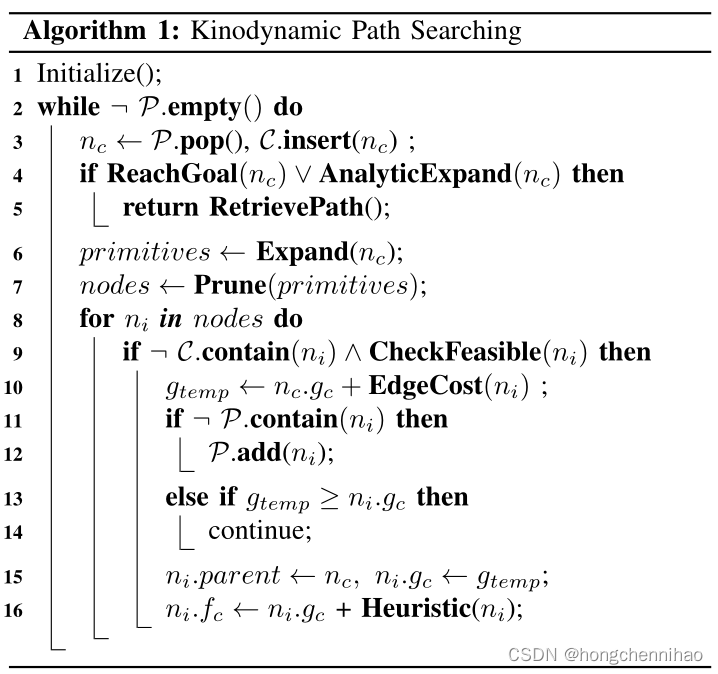
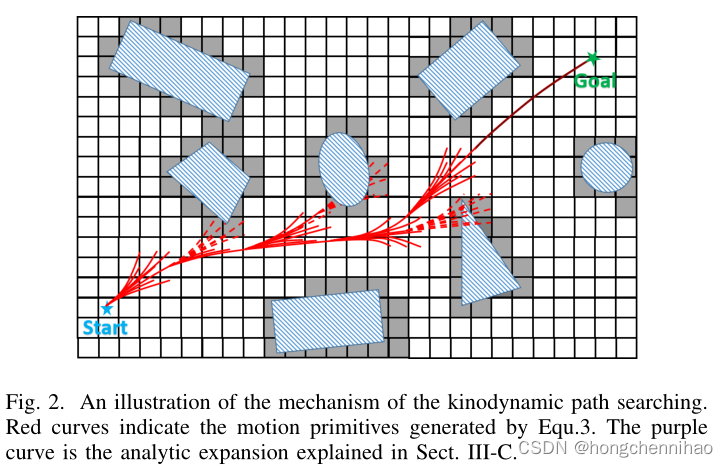如算法 1 和图 2 所示，搜索循环和标准 A 算法类似，其中 $P$ 和 $C$ 分别为开集和闭集。用符合四旋翼的运动基元代替直线作为边。一个结构 $Node$ 被用来记录一个基元、基元结束的体素和 $g_c$ 和 $f_c$ 代价（Sect. III-B）。基元迭代地扩展（Expand()）体素网格地图，除了具有最小的 $f_c$ 的基元，在同一体素网格结束的其他基元都将被修剪（Prune()）。之后 CheckFeasible() 会检查剩下的基元的安全性和动力学可行性。这个过程一直到有基元抵达终点或 AnalyticExpand() 成功为止。

基元生成

首先讨论 Expand() 中使用的运动基元的生成。四旋翼系统的微分平坦特性允许使用三个一维时间参数化多项式函数来表示轨迹[1]。
$$p(t):=[p_x(t),p_y(t),p_z(t){]}^T,p_{\mu }(t)=\sum _{k=0}^K{a}_k{t}^k$$
其中 μ ∈ { x , y , z } \mu \in \{x,y,z\} μ∈{x,y,z}。从四旋翼系统的角度来看，它对应于一个线性时不变(LTI)系统。让$\mathbf{x}(t):=[\mathbf{p}(t{)}^{\top },\dot{\mathbf{p}}(t{)}^{\top },\cdot \cdot \cdot ,{\mathbf{p}}^{(n-1)}(t{)}^{\top }{]}^{\top }\in \mathcal{X}\subset {\mathbb{R}}^{3n}$ 作为状态向量。让 $\mathbf{u}(t):={\mathbf{p}}^{(n)}\left(t\right)\in \mathcal{U}:={\left[-u_{\max },u_{\max }\right]}^3\subset {\mathbb{R}}^3$ 作为控制输入。状态空间模型可以被定义为：
x ˙ = A x + B u A = [ 0 I 3 0 ⋯ 0 0 0 I 3 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 ⋯ ⋯ 0 I 3 0 ⋯ ⋯ 0 0 ] , B = [ 0 0 ⋮ 0 I 3 ]

$$\begin{aligned} \dot{\mathbf{x}} & =\mathbf{A} \mathbf{x}+\mathbf{B u} \\ \mathbf{A} & =\left[\begin{array}{ccccc} \mathbf{0} & \mathbf{I}_{3} & \mathbf{0} & \cdots & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{I}_{3} & \cdots & \mathbf{0} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \mathbf{0} & \cdots & \cdots & \mathbf{0} & \mathbf{I}_{3} \\ \mathbf{0} & \cdots & \cdots & \mathbf{0} & \mathbf{0} \end{array}\right], \quad \mathbf{B}=\left[\begin{array}{c} \mathbf{0} \\ \mathbf{0} \\ \vdots \\ \mathbf{0} \\ \mathbf{I}_{3} \end{array}\right] \end{aligned}$$ x˙A​=Ax+Bu= ​00⋮00​I3​0⋮⋯⋯​0I3​⋮⋯⋯​⋯⋯⋱00​00⋮I3​0​ ​,B= ​00⋮0I3​​ ​​
状态方程的完全解为：
$$\mathbf{x}(t)=e^{\mathbf{A}t}\mathbf{x}(0)+{\int }_0^t{e}^{\mathbf{A}(t-\tau )}{\mathbf{B}}_{\mathbf{U}}(\tau )d\tau$$
上述方程给出了初始状态 $为x(0)$，控制输入为 $u(t)$ 的四旋翼系统的轨迹。
在 Expand() 中，给定无人机的当前状态，在持续时间 $\tau$ 内应用一组离散的控制输入 ${\mathcal{U}}_D\subset \mathcal{U}$。在实际中，我们选择 $n=2$，这对应于一个二重积分。每个轴$[-u_{max},u_{max}]$ 被均匀离散为 $\left\{-u_{max},-\frac{r-1}{r}{u}_{max},\cdot \cdot \cdot ,\frac{r-1}{r}{u}_{max},u_{max}\right\}$，这会得到 $(2r+1{)}^3$ 个基元。

实际代价和启发式代价

想要得到在时间和控制代价上都最优的轨迹，所以定义轨迹的代价为：
$$\mathcal{J}(T)={\int }_0^T\Vert \mathbf{u}(t){\Vert }^{2}dt+\rho T$$
在这个定义下，EdgeCost() 计算由离散输入 $u(t)=u_d$ 和持续时间 $\tau$（$e_c=(||{\mathbf{u}}_d|{|}^2+\rho )\tau$）生成的运动基元的代价。
用 $g_c$ 表示从开始状态 $x_s$ 到当前状态 $x_c$ 的一条最优路径的实际代价。最优路径由 $J$ 个基元组成，则：$g_c={\sum }_{j=1}^J(||{\mathbf{u}}_{dj}|{|}^2+\rho )\tau$。
设计了一个启发项 Heuristic()。通过应用 Pontryagins 最小化原理[16]，计算了从 $x_c$ 到目标状态 $x_g$ 的最小化 $\mathcal{J}(T)$ 的封闭轨迹：
p μ ∗ ( t ) = 1 6 α μ t 3 + 1 2 β μ t 2 + v μ c + p μ c [ α μ β μ ] = 1 T 3 [ − 12 6 T 6 T − 2 T 2 ] [ p μ g − p μ c − v μ c T v μ g − v μ c ] J ∗ ( T ) = ∑ μ ∈ { x , y , z } ( 1 3 α μ 2 T 3 + α μ β μ T 2 + β μ 2 T )

$$\begin{aligned} p_{\mu}^{*}(t) & =\frac{1}{6} \alpha_{\mu} t^{3}+\frac{1}{2} \beta_{\mu} t^{2}+v_{\mu c}+p_{\mu c} \\ {\left[\begin{array}{c} \alpha_{\mu} \\ \beta_{\mu} \end{array}\right] } & =\frac{1}{T^{3}}\left[\begin{array}{cc} -12 & 6 T \\ 6 T & -2 T^{2} \end{array}\right]\left[\begin{array}{c} p_{\mu g}-p_{\mu c}-v_{\mu c} T \\ v_{\mu g}-v_{\mu c} \end{array}\right] \\ \mathcal{J}^{*}(T) & =\sum_{\mu \in\{x, y, z\}}\left(\frac{1}{3} \alpha_{\mu}^{2} T^{3}+\alpha_{\mu} \beta_{\mu} T^{2}+\beta_{\mu}^{2} T\right) \end{aligned}$$ pμ∗​(t)[αμ​βμ​​]J∗(T)​=61​αμ​t3+21​βμ​t2+vμc​+pμc​=T31​[−126T​6T−2T2​][pμg​−pμc​−vμc​Tvμg​−vμc​​]=μ∈{x,y,z}∑​(31​αμ2​T3+αμ​βμ​T2+βμ2​T)​
其中，$p_{\mu c},v_{\mu c},p_{\mu g},v_{\mu g}$ 是当前和目标的位置和速度。为找到代价最小的最优时间 $T$，将 ${\alpha }_{\mu },{\beta }_{\mu }$ 代入 ${\mathcal{J}}^{\ast }(T)$ 并找到 $\frac{\partial {\mathcal{J}}^{\ast }(T)}{\partial T}=0$ 的根。选取代价最小记为 $min{\mathcal{J}}^{\ast }$并且轨迹可行的根，记为 $T_h$。使用 ${\mathcal{J}}^{\ast }(T_h)$ 作为启发项 $h_c$。最后，$f_c$：$f_c=g_c+h_c=g_c+{\mathcal{J}}^{\ast }(T_h)$。

分析扩展

因为输入是离散的，所以很难找到一个完全处于目标状态的基元端点。为了弥补这一缺陷并加速搜索，引入了一个分析扩展方案。当一个节点从开集弹出的时候，会使用与 Sec.III-B 中相同的方法计算一条从 $x_c$ 到 $x_g$ 的轨迹。如果它通过了安全和动力学可行性检查，搜索会被提前终止。这个策略对于提高效率是有效的尤其在稀疏环境中，因为它有更高的成功率并且会更早地终止搜索。

B 样条轨迹优化

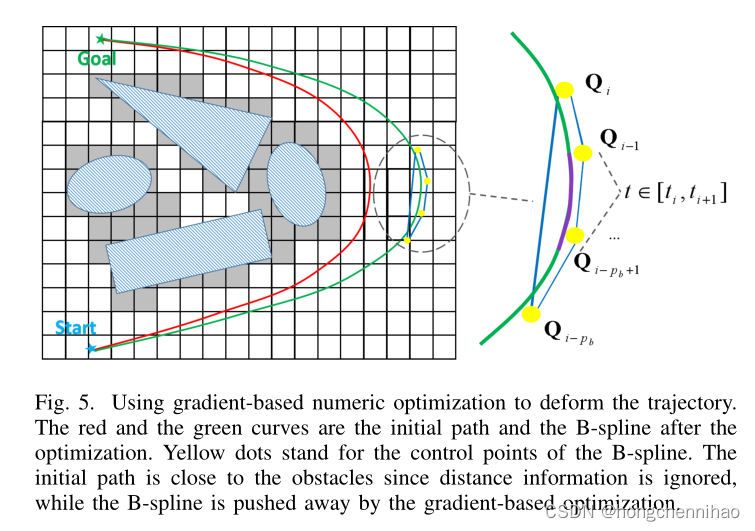
由路径搜索所产生的路径可能不是最优的。此外，因为自由空间的距离信息被忽略会导致路径经常会接近障碍物（如图 5）。因此，采用提出的 B 样条优化来提高路径的平滑度和间隙。利用 B 样条的凸包性融合来自欧氏距离场和动态约束的梯度信息，它可以在很短的时间内收敛，生成平滑、安全和动态可行的轨迹。

均匀 B 样条

B 样条是一个单独由它的阶数 $p_b$，$N+1$ 个控制点 $Q_0,Q_1,...,Q_N$ 集合以及一个节点向量$[t_0,t_q,...,t_M]$ 所决定的分段多项式，其中 $Q_i\in {\mathbb{R}}^3,t_m\in \mathbb{R},M=N+p_b+1$。B 样条轨迹用时间 $t$ 来参数化，$t\in [t_{pb},t_{M-pb}]$。对于均匀 B 样条，每个节点跨度都是相同的，$\Delta t_m=t_{m+1}-t_m$。为求出 $t\in [t_m,t_{m+1}]\subset [t_{p_b},t_{M-p_b}]$ 时刻的位置，首先将 $t$ 归一化为 $s(t)=(t-t_m)/\Delta t$。之后采用矩阵表示来求出位置[17]：
p ( s ( t ) ) = s ( t ) ⊤ M p b + 1 q m s ( t ) = [ 1 s ( t ) s 2 ( t ) ⋯ s p b ( t ) ] ⊤ q m = [ Q m − p b Q m − p b + 1 Q m − p b + 2 ⋯ Q m ] ⊤

$$\begin{array}{l} \mathbf{p}(s(t))=\mathbf{s}(t)^{\top} \mathbf{M}_{p_{b}+1} \mathbf{q}_{m} \\ \mathbf{s}(t)=\left[\begin{array}{lllll} 1 & s(t) & s^{2}(t) & \cdots & s^{p_{b}}(t) \end{array}$$ \right]^{\top} \\ \mathbf{q}_{m}=\left[ $$\begin{array}{lllll} \mathbf{Q}_{m-p_{b}} & \mathbf{Q}_{m-p_{b}+1} & \mathbf{Q}_{m-p_{b}+2} & \cdots & \mathbf{Q}_{m} \end{array}$$ \right]^{\top} \end{array} p(s(t))=s(t)⊤Mpb​+1​qm​s(t)=[1​s(t)​s2(t)​⋯​spb​(t)​]⊤qm​=[Qm−pb​​​Qm−pb​+1​​Qm−pb​+2​​⋯​Qm​​]⊤​
其中，$M_{pb+1}$ 是一个由 $p_b$ 决定的常数矩阵。本文中，$p_b$ 被设置为 3。导数的计算是完全相同的，因为 B 样条的导数也是 B 样条。
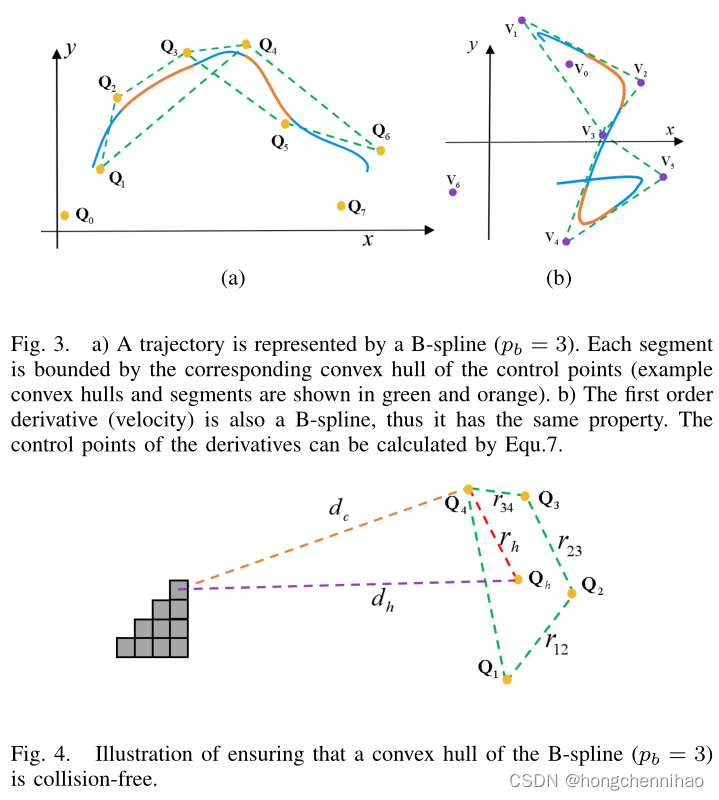
B 样条曲线的凸包特性（图3）对于优化公式的设计至关重要。我们在 Sect.IV -B 节中表明，它对于确保整个轨迹的动态可行性和安全性非常有用。

B.凸包性

如图3，本文广泛使用凸包性来确保动态可行性和安全性。
动态可行性要求约束所有的速度和加速度控制点 { V 0 , V 1 , . . . , V N − 1 } \{V_0,V_1,...,V_{N-1}\} {V0​,V1​,...,VN−1​}， { A 0 , A 1 , . . . , A N − 2 } \{A_0,A_1,...,A_{N-2}\} {A0​,A1​,...,AN−2​}，使其满足 $V_i\in [-v_{max},v_{max}{]}^3$， $A_i\in [-a_{max},a_{max}{]}^3$。$V_i,A_i$ 由下式计算，其中 $\Delta t$ 是节点跨度。
$${\mathbf{V}}_i=\frac{1}{\Delta t}({\mathbf{Q}}_{i+1}-{\mathbf{Q}}_i),{\mathbf{A}}_i=\frac{1}{\Delta t}({\mathbf{V}}_{i+1}-{\mathbf{V}}_i)$$
为了 B 样条的安全性，需要确保所有的凸包都是无碰撞的。即需要确保任意一个被占据的体素与任一个凸包上的点 $Q_h$ 之间的距离 $d_h>0$ （如图4）。
根据三角形不等式，可知：$d_h>d_c-r_h$，$d_c$ 是任意两个体素和控制点之间的距离。因为 $Q_h$ 是凸包内的点，所以也有：$r_h\le r_{12}+r_{23}+r_{34}$。两式相结合，则有：$d_h>d_c-(r_{12}+r_{23}+r_{34})$。因此，只需要保证：
d c > 0 , r j , j + 1 < d c / 3    ( j ∈ { 1 , 2 , 3 } ) ( 8 ) d_{c}>0,\quad r_{j,j+1}<d_{c}/3\ \ (j\in\{1,2,3\}) \quad(8) dc​>0,rj,j+1​<dc​/3  (j∈{1,2,3})(8)
之后就可以保证凸包是无碰撞的。

C.问题描述

对于由 $N+1$ 个控制点定义的 $p_b$ 阶 B 样条轨迹，优化 $N+1-2p_b$ 个控制点的子集 { Q p b , Q p b + 1 , . . . , Q N − p b } \{Q_{p_b},Q_{p_b+1},...,Q_{N-p_b}\} {Qpb​​,Qpb​+1​,...,QN−pb​​}。首位的 $p_b$ 个控制点不应该被改变，因为它们决定了边界状态。总的代价函数被定义为：
$$f_{total}={\lambda }_1{f}_s+{\lambda }_2{f}_c+{\lambda }_3(f_v+f_a)$$
其中，$f_s$ 和 $f_c$ 平滑度和碰撞代价， $f_v$ 和 $f_a$ 是速度和加速度的柔性限制， ${\lambda }_1，{\lambda }_2，{\lambda }_3$ 用来平衡平滑度、安全性和动态可行性。
通过一个捕捉轨迹几何信息的函数来定义平滑度代价 $f_s$，并且不依赖时间分配，与最近采用 snap 或 jerk 平方的积分的工作不同。原因是在优化之后时间分配可能会调整（Sect. V）。这可能会改变轨迹的导数改变，使优化后的 snap(jerk) 不那么有意义。使用弹性带代价函数（elastic
band cost function）[18, 19]（控制点$Q_{p_b-2}，Q_{p_b-1}$ 和 $Q_{N-p_b+1}，Q_{N-p_b+2}$ 没有被优化但是需要评估其总体平滑度。同样地，他们中的一些点作为常量被包含进等式 14，来计算导数）：
$$f_s=\sum _{i=p_b-1}^{N-p_b+1}\Vert \underset{{\mathbf{F}}_{i+1,i}}{\underbrace{\left({\mathbf{Q}}_{i+1}-{\mathbf{Q}}_i\right)}}+\underset{{\mathbf{F}}_{i-1,i}}{\underbrace{\left({\mathbf{Q}}_{i-1}-{\mathbf{Q}}_i\right)}}{\Vert }^2$$
从物理的角度，这个公式将一条轨迹看作一个弹性带，其中每个项 $F_{i+1,i}=Q_{i+1}-Q_i$ 和 $F_{i-1,i}=Q_{i-1}-Q_i$ 是分别连接节点 $Q_{i+1}，Q_i$ 和 $Q_{i-1}，Q_i$的两个弹簧的合力。如果所有项都等于 0，那么所有的控制点将均匀地分布在一条直线上，这是理想的平滑度。
同样地，碰撞代价表示为障碍物作用在每个控制点上的排斥力：
$$f_c=\sum _{i=p_b}^{N-p_b}{F}_c(d(Q_i))$$
其中，$d(Q_i)$ 是 $Q_i$ 与最近的障碍物的距离。$F_c$ 是一个可微的潜在代价函数，其中 $d_{thr}$ 是指定障碍物清除的阈值：
F c ( d ( Q i ) ) = { ( d ( Q i ) − d t h r ) 2 d ( Q i ) ≤ d t h r 0 d ( Q i ) > d t h r ( 12 ) F_{c}(d({\bf Q}_{i}))=\left\{

$$\begin{array}{c c}{ {(d({\bf Q}_{i})-d_{t h r})^{2}}}&{ {d({\bf Q}_{i})\le d_{t h r}}}\\ { {0}}&{ {d({\bf Q}_{i})>d_{t h r}}}\end{array}$$ \right. \quad (12) Fc​(d(Qi​))={(d(Qi​)−dthr​)20​d(Qi​)≤dthr​d(Qi​)>dthr​​(12)
如 Sect.IV-B，要使轨迹无碰撞，等式 8 必须被满足。因为碰撞代价会将控制点推离障碍物，所以 $d_c>0$ 是显然满足的。同时， $r_{j,j+1}$ 是只依赖于 B 样条参数化的可调参数。在实际中，只要选择足够小的 r j , j + 1 , ( j ∈ { 0 , 1 , . . . , N } r_{j,j+1},(j \in \{0,1,...,N\} rj,j+1​,(j∈{0,1,...,N}，在大多数情况下轨迹是安全的（在我们的实现中 $r_{j,j+1}<0.2$）。在环境十分混乱等极端情况下可能会失效。即便如此，可以选择更小的 $r_{j,j+1}$ 来重新参数化 B 样条曲线，之后等式 8 可以被满足。
采用与等式 12类似的方程，沿着轨迹超过最大允许值 $v_{max}，a_{max}$ 方向惩罚速度和加速度。一维速度 $v_{\mu }$ 的惩罚是：
$$F_v(v_{\mu })=\{\begin{array}{cc}{\left(v_{\mu }^2-v_{max}^2\right)}^2& v_{\mu }^2>v_{max}^2\\ 0& v_{\mu }^2\le v_{max}^2\end{array}$$
其中， μ ∈ { x , y , z } \mu \in \{x,y,z\} μ∈{x,y,z}。加速度惩罚有相同的形式。应用凸包性（图 3），定义了 $f_v，f_a$，使不可行的速度和加速度控制点会被惩罚：
f v = ∑ μ ∈ { x , y , z } ∑ i = p b − 1 N − p b F v ( V i μ ) , f a = ∑ μ ∈ { x , y , z } ∑ i = p b − 2 N − p b F a ( A i μ ) f_{v}=\sum_{\substack{\mu \in \\\{x, y, z\}}} \sum_{i=p_{b}-1}^{N-p_{b}} F_{v}\left(V_{i \mu}\right), \quad f_{a}=\sum_{\substack{\mu \in \\\{x, y, z\}}} \sum_{i=p_{b}-2}^{N-p_{b}} F_{a}\left(A_{i \mu}\right) fv​=μ∈{x,y,z}​∑​i=pb​−1∑N−pb​​Fv​(Viμ​),fa​=μ∈{x,y,z}​∑​i=pb​−2∑N−pb​​Fa​(Aiμ​)

V.时间调整

虽然在路径搜索和优化中约束了动力学可行性，有时仍然会得到不可行的轨迹。基本的原因是梯度信息倾向于延长整个轨迹，同时使其远离障碍物。因此，无人机必须飞行更激进以便在相同时间内飞行更远的距离，如果原来的运动已经逼近物理极限，这会不可避免地导致过度激进的运动。
为保证动态可行性，采用了一种基于导数控制点和非均匀 B 样条时间分配（节点跨度）之间关系的时间调整方法。由于这种关系，可以通过调整相关的时间分配来改变所期望的飞行激烈程度。因此，可以在没有过度保守的约束的情况下确保动态可行性。
首先介绍了时间调整的数学基础。然后提出了 Alg. 2 来解决过于激进的轨迹。

A.非均匀 B 样条

非均匀 B 样条是一种更一般的 B 样条。它与均匀 B 样条唯一的不同是它的每一个节点跨度 $\Delta t_m=t_{m+1}-t_m$ 是相互独立的。非均匀 B 样条的一阶 导数$V_i^{{}^{\prime }}$ 和二阶导数 $A_i^{{}^{\prime }}$ 的控制点可由下式计算：
V i ′ = p b ( Q i + 1 − Q i ) t i + p b + 1 − t i + 1 , A i ′ = ( p b − 1 ) ( V i + 1 ′ − V i ′ ) t i + p b + 1 − t i + 2 ( 15 )

$$\begin{array}{c c}{ {\displaystyle V_{i}^{\prime} = \frac{p_{b}(Q_{i+1}-Q_{i})}{t_{i+p_{b}+1}-t_{i+1}},}}&{ {\displaystyle\mathbf{A}_{i}^{\prime} = \frac{(p_{b}-1)(V_{i+1}^{\prime}-V_{i}^{\prime})}{t_{i+p_{b}+1}-t_{i+2}}}}\end{array}$$ \quad (15) Vi′​=ti+pb​+1​−ti+1​pb​(Qi+1​−Qi​)​,​Ai′​=ti+pb​+1​−ti+2​(pb​−1)(Vi+1′​−Vi′​)​​(15)
根据凸包性，要保证由非均匀 B 样条表示的轨迹的动态可行性，只需要保证一阶和二阶导数的所有控制点在可行域内即可。在 Sect. V-B 中，展示了通过改变不可行控制点相关的节点跨度即可达到这一目的。

B.节点跨度调整

使 ${\mathbf{V}}_i^{\prime }=[{\mathbf{V}}_{i,x}^{\prime },{\mathbf{V}}_{i,y}^{\prime },{\mathbf{V}}_{i,z}^{\prime }{]}^{\top }$ 为不可行的速度控制点。$V_{i,\mu }^{{}^{\prime }}$ 是最大的不可行分量并且 $\mid V_{i,\mu }^{\prime }\mid =v_m$。从等式 15 可知，$V_{i,\mu }^{{}^{\prime }}$ 受持续时间 $t_{i+p_b+1}-t_{i+1}$ 影响。如果改变持续时间为 ${\hat{\hat{t}}}_{i+p_b+1}-{\hat{t}}_{i+1}={\mu }_v(t_{i+p_b+1}-t_{i+1})$，$V_{i,\mu }^{{}^{\prime }}$ 也将改变为：
$$\begin{gathered} {\hat{V}}_{i,\mu }=\frac{Pb}{{\hat{t}}_{i+p_b+1}-{\hat{t}}_{i+1}}((Q_{i+1,\mu }-Q_{i,\mu }) \\ =\frac{1}{{\mu }_v}\frac{p_b}{t_{i+p_b+1}-t_{i+1}}(Q_{i+1,\mu }-Q_{i,\mu })=\frac{1}{{\mu }_v}{V}_{i,\mu }^{\prime } \end{gathered}$$
因此，如果我们设 ${\mu }_v=\frac{v_m}{v_{max}}$，之后速度是可行的，因为 $\mid {\hat{V}}_{i,\mu }\mid =\frac{v_{max}}{v_m}\mid V_{i,\mu }^{{}^{\prime }}=v_{max}\in [-v_{max},v_{max}]$。
加速度可行性的实施是类似的。$A_{i,\mu }^{{}^{\prime }}$ 实际受 $t_{i+p_b+2}-t_{i+1}$，因为它与 $V_{i,\mu }^{{}^{\prime }}$ 和 $V_{i+1,\mu }^{{}^{\prime }}$ 相连接。对于 m ∈ { i + 1 , i + 2 , . . . , i + p b + 1 } m \in \{i+1,i+2,...,i+p_b+1\} m∈{i+1,i+2,...,i+pb​+1}，改变 $\Delta t_m=t_{m+1}-t_m$ 为 $\Delta {\hat{t}}_m={\mu }_a\Delta t_m$，可得：
A ^ i , μ = p b − 1 t ^ i + p b + 1 − t ^ i + 2 ( V ^ i + 1 , μ − V ^ i , μ ) = 1 μ a p b − 1 t i + p b + 1 − t i + 2 ( 1 μ a V i + 1 , μ ′ − 1 μ a V i , μ ′ ) = 1 μ a 2 p b − 1 t i + p b + 1 − t i + 2 ( V i + 1 , μ ′ − V i , μ ′ ) = 1 μ a 2 A i , μ ′

$$\begin{aligned} \hat{A}_{i, \mu} & =\frac{p_{b}-1}{\hat{t}_{i+p_{b}+1}-\hat{t}_{i+2}}\left(\hat{V}_{i+1, \mu}-\hat{V}_{i, \mu}\right) \\ & =\frac{1}{\mu_{a}} \frac{p_{b}-1}{t_{i+p_{b}+1}-t_{i+2}}\left(\frac{1}{\mu_{a}} V_{i+1, \mu}^{\prime}-\frac{1}{\mu_{a}} V_{i, \mu}^{\prime}\right) \\ & =\frac{1}{\mu_{a}^{2}} \frac{p_{b}-1}{t_{i+p_{b}+1}-t_{i+2}}\left(V_{i+1, \mu}^{\prime}-V_{i, \mu}^{\prime}\right)=\frac{1}{\mu_{a}^{2}} A_{i, \mu}^{\prime} \end{aligned}$$ A^i,μ​​=t^i+pb​+1​−t^i+2​pb​−1​(V^i+1,μ​−V^i,μ​)=μa​1​ti+pb​+1​−ti+2​pb​−1​(μa​1​Vi+1,μ′​−μa​1​Vi,μ′​)=μa2​1​ti+pb​+1​−ti+2​pb​−1​(Vi+1,μ′​−Vi,μ′​)=μa2​1​Ai,μ′​​
类似地，使 ${\mu }_a=(\frac{a_m}{a_{max}}{)}^{\frac{1}{2}}$，可得 $\mid {\hat{A}}_{i,\mu }\mid =\frac{a_{max}}{a_m}\mid A_{i,\mu }^{\prime }\mid =a_{max}\in [-a_{max},a_{max}]$。

C.迭代时间调整

基于 Sect. V-B，采用 Alg. 2 来实现动态可行性。它迭代地找到轨迹中不可行的速度和加速度控制点 $\mathcal{V}\text{ and }\mathcal{A}$（第 2 行），并调整相关的节点跨度（第 3-10 行）。因为一个结点跨度 $∆t_m$ 会影响几个控制点，反之亦然，用两个略大于1的常数 ${\alpha }_v$ 和 ${\alpha }_a$ 来限定 ${\mu }_v$ 和 ${\mu }_a$ （第5，9行）可以防止任何时间跨度被过度延长。