二叉树详解（Java）_java二叉树算法详解

1、树

相信大家对于二叉树的概念并不陌生，什么是树？什么是二叉树？

1.1、树的定义

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

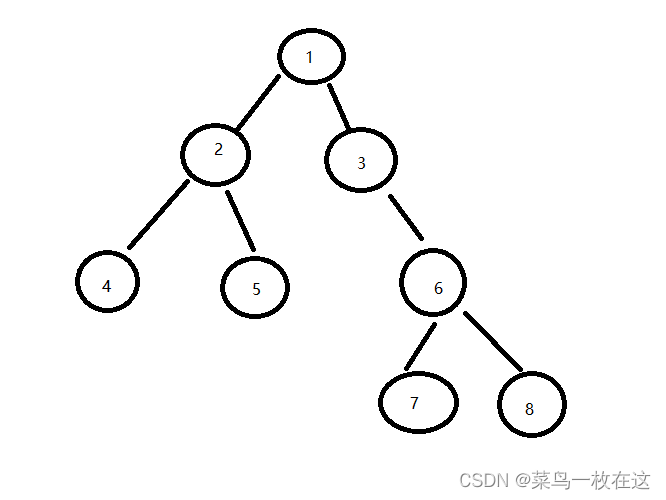
上图就是一颗正常的树，而对于只有一个节点的，也可以叫做单节点树

1.2、树的一些定义

• 节点的度：一个节点含有的子树的个数，叫做该节点的度。
• 叶节点和终端节点：度为零的节点。
• 双亲结点或父节点：如图，C为G的父节点。
• 孩子节点或子节点：如图，G为C的子节点。
• 兄弟节点：拥有相同父节点的节点称为兄弟节点。
• 树的度：一棵树中最大的节点的度称为树的度。
• 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推。
• 树的高度或深度：树中节点的最大层次，如图，高度为4。
• 祖先：从跟到该节点所经分支上的所有节点。A是所有节点的祖先。
• 森林：由m（m>0）棵互不相交的树的集合称为森林。

 1.3、树的表示

因为它是一种非线性的存储结构，所以类似于链表的存储形式，它有很多种表现形式,这里用最常见的子节点数组的形式展示：

class TreeNode {
    int val;
    TreeNode[] children;
 
    TreeNode() {
    }
 
    TreeNode(int val) {
        this.val = val;
    }
 
    TreeNode(int val, TreeNode[] children) {
        this.val = val;
        this.children = children;
    }
}

存储的结构为（这里以上面那个图为例）：

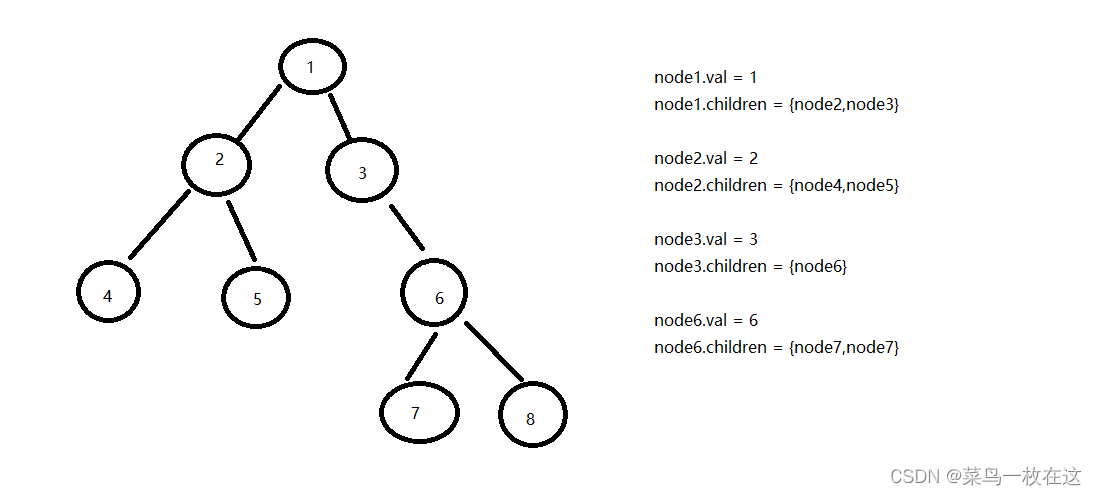
 那些值的操作这里就不做描述了，节点为空的也不做描述了。

2、二叉树

2.1、二叉树的概念

一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。

二叉树的特点：

1. 每个节点最多有两棵子树，即不存在超过度为2的节点。
2. 二叉树的子树有左右之分，且左右不能颠倒。

2.2、一些特殊的二叉树

满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。

 完全二叉树：完全二叉树是由满二叉树引出的。满二叉树要求每一层的节点数都达到最大值，完全二叉树仅要求除最后一层外的节点数达到最大值，也就是说最后一层可以不满。我们可以把满二叉树看错特殊的完全二叉树。所以满二叉树是特殊的完全二叉树。

 2.3、二叉树的性质

若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1) 个结点。
若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h- 1。
任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0＝n2＋1
若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=Log2(n+1)
对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：
（1）. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点

（2）. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子

（3）. 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

 2.4、二叉树的表示

其实二叉树的表示就和树的表示差不多，区分节点而已，表示如下

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
 
    TreeNode() {
    }
 
    TreeNode(int val) {
        this.val = val;
    }
 
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

3、二叉树的遍历

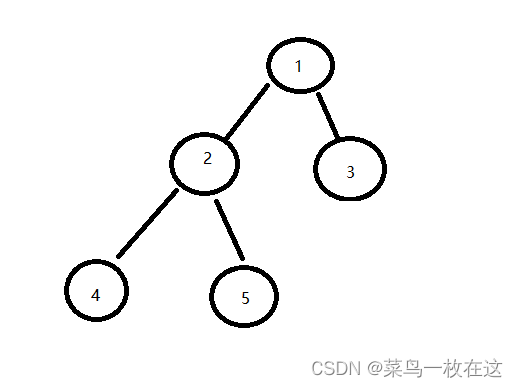
 下面都以此树为例子。

3.1、前序遍历

先访问根节点，再访问左节点，左节点不为空就递归前序遍历，再访问右节点，右节点不为空就递归前序遍历

顺序为：1 2 4 5 3

代码实现：

public static void preorderTraversal(TreeNode root) {
        if(root == null){
            return;
        }
        System.out.println(root.val);
        preorderTraversal(root.left);
        preorderTraversal(root.right);
    }

3.2、中序遍历

先访问左子节点，左子节点不为空就递归中序遍历，再访问根节点，然后再访问右子节点，右子节点不为空就递归中序遍历

顺序为：4 2 5 1 3

代码实现：

    public static void inorder(TreeNode1 root){
        if(root==null){
            return;
        }
        inorder(root.left);
        System.out.println(root.val);
        inorder(root.right);
    }

3.3、后序遍历

先访问左子节点，左子节点不为空就递归后序遍历，再访问右子节点，右子节点不为空就递归后序遍历，然后再访问根节点

顺序为：4 5 2 3 1

代码实现：

    public static void postorder(TreeNode1 root){
        if(root==null){
            return;
        }
        postorder(root.left);
        postorder(root.right);
        System.out.println(root.val);
    }