AllinToyou

这个屌丝很懒，什么也没留下！

热门标签

平衡二叉树详解-java实现

作者：AllinToyou | 2024-05-27 13:01:29

踩

平衡二叉树详解-java实现

前置知识：

二叉查找树

平衡二叉树（Balanced Binary Tree）又被称为AVL树（有别于AVL算法），且具有以下性质：

它是一棵空树或它的左右两个子树的高度差的绝对值不超过1
左右两个子树都是一棵平衡二叉树。

这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

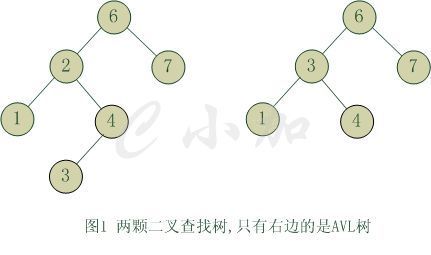
平衡二叉树大部分操作和二叉查找树类似，主要不同在于插入、删除的时候平衡二叉树的平衡可能被改变，并且只有从那些插入点到根结点的路径上的结点的平衡性可能被改变，因为只有这些结点的子树可能变化。

插入平衡二叉树不平衡的情形：

把需要重新平衡的结点叫做α，由于任意两个结点最多只有两个儿子，因此高度不平衡时，α结点的两颗子树的高度相差2.容易看出，这种不平衡可能出现在下面4中情况中：

1.对α的左儿子的左子树进行一次插入

2.对α的左儿子的右子树进行一次插入

3.对α的右儿子的左子树进行一次插入

4.对α的右儿子的右子树进行一次插入

实际上上面四种情况可以总结为LL、LR、RL、RR

以LL为例，它代表根节点的左侧子节点高，左侧子节点的左侧子节点高。其他三种情况同LL。

/**
 * 非平衡状态的判断，判断该节点属于LL、LR、RL、RR，并针对不同情况进行旋转平衡
 * @param node 从下向上第一次出现非平衡状态的节点
 */
public void unbalancedState(BalancedBinarySearchTreeNode node){
    if (node.left.hight() == node.hight()){
        if (node.left.left.hight()==node.left.hight()){
            //LL
            rightRotation(node);
        }else{
            //LR
            leftRightRotation(node);
        }
    }else {
        if (node.right.left.hight()==node.right.hight()){
            //RL
            rightLeftRotation(node);
        }else {
            //RR
            leftRoatation(node);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

情形1和情形4是关于α的镜像对称，二情形2和情形3也是关于α的镜像对称，因此理论上看只有两种情况，但编程的角度看还是四种情形。

第一种情况是插入发生在“外边”的情形（左左或右右），该情况可以通过一次单旋转完成调整；第二种情况是插入发生在“内部”的情形（左右或右左），这种情况比较复杂，需要通过双旋转来调整。

正如上面所说，平衡二叉树插入导致不平衡状态可以总结为上述四种情况，其他情况都是上述情况子节点存在与否变种而来，但不影响分析。

调整措施：

一、单旋转

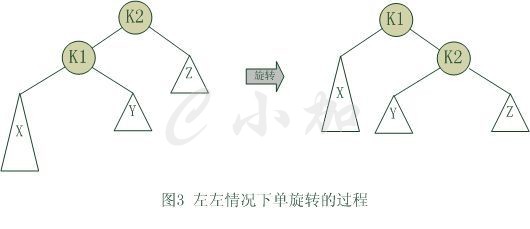
上图是左左的情况，k2结点不满足平衡性，它的左子树k1比右子树z深两层，k1子树中更深的是k1的左子树x，因此属于左左情况。

为了恢复平衡，我们把x上移一层，并把z下移一层，但此时实际已经超出了AVL树的性质要求。为此，重新安排结点以形成一颗等价的树。为使树恢复平衡，我们把k2变成这棵树的根节点，因为k2大于k1，把k2置于k1的右子树上，而原本在k1右子树的Y大于k1，小于k2，就把Y置于k2的左子树上，这样既满足了二叉查找树的性质，又满足了平衡二叉树的性质。

这种情况称为单旋转。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oeKCWqpe-1631694090874)(平衡二叉树详解 bingo.assets/image-20210915104751168.png)]

    //单旋转
    /**
     * 单旋转-右旋
     *                  6                                               3
     *          3                 7                             1               6
     *      1        4                           =>                2         4      7
     *        2
     * 步骤两步：
     * 1.将3提为root.
     * 2.将3的右子树转移给6作为左子树
     * 应用场景：在插入、删除之前平衡二叉查找树是空树或平衡树
     *          插入或删除后才产生非平衡状态
     * @param node：6，插入节点到6之间非平衡
     */
    public BalancedBinarySearchTreeNode rightRotation(BalancedBinarySearchTreeNode node){
        BalancedBinarySearchTreeNode newRoot = node.left;
        newRoot.parent=node.parent;

        node.left = newRoot.right;
        newRoot.right.parent=node;

        newRoot.right = node;
        node.parent=newRoot;

        return newRoot;
    }

    /**
     * 单旋转-左旋
     * @param node
     * @return
     */
    public BalancedBinarySearchTreeNode leftRoatation(BalancedBinarySearchTreeNode node){
        BalancedBinarySearchTreeNode newRoot = node.right;
        newRoot.parent=node.parent;

        node.right = newRoot.left;
        newRoot.left.parent = node;

        newRoot.left = node;
        node.parent=newRoot;
        return newRoot;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

二、双旋转

对于左右和右左两种情况，单旋转不能解决问题，要经过两次旋转。

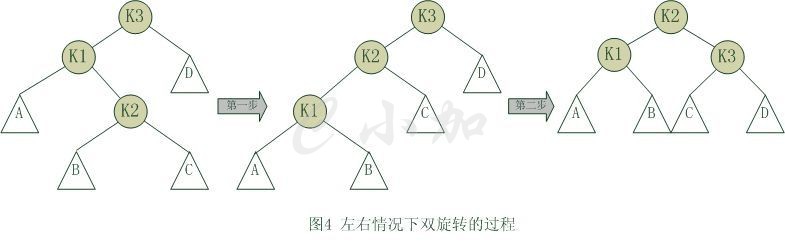
对于上图情况，为使树恢复平衡，我们需要进行两步，第一步，把k1作为根，进行一次右右旋转，旋转之后就变成了左左情况，所以第二步再进行一次左左旋转，最后得到了一棵以k2为根的平衡二叉树。

    //双旋转

    /**
     * 双旋转-左右旋
     *                    6                           6
     *              2           7    =>         4           7
     *          1      4                    2
     *               3                    1   3
     *
     *                     4
     *    =>        2           6
     *            1   3            7
     *
     *
     * 步骤：
     * 1.先对左子节点进行一次左旋
     * 2.再对根节点进行一次右旋
     * @param node
     * @return
     */
    public BalancedBinarySearchTreeNode leftRightRotation(BalancedBinarySearchTreeNode node){
        //在单旋的时候已经将节点的parent改过来了
        node.left = leftRoatation(node.left);
        BalancedBinarySearchTreeNode balancedBinarySearchTreeNode = rightRotation(node);
        return balancedBinarySearchTreeNode;
    }
    /**
     * 双旋转-右左旋
     */
    public BalancedBinarySearchTreeNode rightLeftRotation(BalancedBinarySearchTreeNode node){
        node.right = rightRotation(node.right);
        BalancedBinarySearchTreeNode balancedBinarySearchTreeNode = leftRoatation(node);
        return balancedBinarySearchTreeNode;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

三非平衡状态判断

/**
 * 非平衡状态的判断，判断该节点属于LL、LR、RL、RR，并针对不同情况进行旋转平衡
 * @param node 从下向上第一次出现非平衡状态的节点
 */
public void unbalancedState(BalancedBinarySearchTreeNode node){
    if (node.left.hight() == node.hight()){
        if (node.left.left.hight()==node.left.hight()){
            //LL
            rightRotation(node);
        }else{
            //LR
            leftRightRotation(node);
        }
    }else {
        if (node.right.left.hight()==node.right.hight()){
            //RL
            rightLeftRotation(node);
        }else {
            //RR
            leftRoatation(node);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

AVL树的删除操作：

同插入操作一样，删除结点时也有可能破坏平衡性，这就要求我们删除的时候要进行平衡性调整。

删除分为以下几种情况：

1.整个二叉树中不包含要删除的节点，搜索结束后直接返回不做处理。
2.删除的节点没有子节点
3.删除的节点有左节点或右节点
4.删除的节点既有左节点又有右节点

下面我们就上面的几种情况进行讨论：

1.整个二叉树中不包含要删除的节点，搜索结束后直接返回不做处理。

2.删除的节点没有子节点

没有子节点，直接将该节点进行删除，对删除的节点向上进行平衡性判断并再平衡。

删除后节点的不平衡情况和插入情况一致，按照插入的再平衡实现删除的再平衡。

3.删除的节点有左节点或右节点

将左节点或右节点插入到删除节点的位置

同样向上找到不平衡节点进行再平衡

4.删除的节点既有左节点又有右节点

分两种情况：

(1)、左子树高度大于右子树高度，将左子树中最大的那个元素赋给当前根节点，然后递归删除左子树中元素值最大的那个节点。

(2)、左子树高度小于右子树高度，将右子树中最小的那个元素赋给当前根节点，然后递归删除右子树中元素值最小的那个节点。

同样，做完删除操作后要进行平衡性判断

再平衡操作

① 将该结点直接从树中删除；

② 其父节点的子树高度的变化将导致父结点平衡因子的变化，通过向上检索并推算其父结点是否失衡；

③ 如果其父结点未失衡，则继续向上检索推算其父结点的父结点是否失衡…如此反复②的判断，直到根结点；如果向上推算过程中发现了失衡的现象，则进行④的处理；

④ 如果其父结点失衡，则判断是哪种失衡类型[LL、LR、RR、RL]，并对其进行相应的平衡化处理。如果平衡化处理结束后，发现与原来以父节点为根结点的树的高度发生变化，则继续进行②的检索推算；如果与原来以父结点为根结点的高度一致时，则可说明父结点的父结点及祖先结点的平衡因子将不会有变化，因此可以退出处理。

删除代码

//二叉查找树搜索
    public boolean contains(int target){
        return contains(target,this)!=null;
    }


    public BalancedBinarySearchTreeNode contains(int target,BalancedBinarySearchTreeNode node){
        if (node==null){
            return null;
        }
        if (target>node.val){
            return contains(target,node.right);
        }else if (target< node.val){
            return contains(target,node.left);
        }else {
            return node;
        }
    }

//平衡二叉树删除
/**
 * 删除节点没有子节点
 * @param node 要删除的节点
 */
public void delectNoChildenNode(BalancedBinarySearchTreeNode node){
    //节点删除
    if (node.parent.left == node){
        node.parent.left = null;
    }else {
        node.parent.right = null;
    }
    //再平衡
    BalancedBinarySearchTreeNode tem = node;
    while (tem.parent==null){
        if (Math.abs(tem.left.hight()- tem.right.hight())>1){
            unbalancedState(tem);
            
        }
        tem = tem.parent;
    }
}

/**
 * 删除节点只有左节点或者右节点
 * @param node 要删除的节点
 */
public void delectWithOneChildenNode(BalancedBinarySearchTreeNode node){
    if (node.parent.left == node){
        if (node.left != null) {
            node.parent.left = node.left;
            node.left.parent = node.parent;
        }
        else {
            node.parent.left = node.right;
            node.right.parent = node.parent;
        }
    }else {
        if (node.left != null) {
            node.parent.right = node.left;
            node.left.parent=node.parent;
        }
        else{
            node.parent.right = node.right;
            node.right.parent=node.parent;
        }
    }
    //再平衡
    BalancedBinarySearchTreeNode tem = node;
    while (tem.parent==null){
        if (Math.abs(tem.left.hight()- tem.right.hight())>1){
            unbalancedState(tem);
            
        }
        tem = tem.parent;
    }
}

/**
 * 删除节点既有左节点又有右节点
 * @param node 要删除的节点
 */
public void delecWithTwoChildenNode(BalancedBinarySearchTreeNode node){
    if (node.left.hight()>node.right.hight()){
        BalancedBinarySearchTreeNode maxNode = getMaxNode(node.left);
        delectNode(maxNode);
        if (node.parent.left==node){
            node.parent.left=maxNode;
            maxNode.parent=node.parent;
            maxNode.left=node.left;
            node.left.parent=maxNode;
            maxNode.right=node.right;
            node.right.parent=maxNode;
        }else {
            node.parent.right=maxNode;
            maxNode.parent=node.parent;
            maxNode.left=node.left;
            node.left.parent=maxNode;
            maxNode.right=node.right;
            node.right.parent=maxNode;
        }

    }else {
        BalancedBinarySearchTreeNode minNode = getMinNode(node.right);
        delectNode(minNode);
        if (node.parent.left==node){
            node.parent.left=minNode;
            minNode.parent=node.parent;
            minNode.left=node.left;
            node.left.parent=minNode;
            minNode.right=node.right;
            node.right.parent=minNode;
        }else {
            node.parent.right=minNode;
            minNode.parent=node.parent;
            minNode.left=node.left;
            node.left.parent=minNode;
            minNode.right=node.right;
            node.right.parent=minNode;
        }
    }
}

/**
 * 删除节点
 * @param target
 */
public void delectNode(int target){
    delectNode(target,this);
}

private void delectNode(int target, BalancedBinarySearchTreeNode node) {
    BalancedBinarySearchTreeNode targetNode = contains(target, node);
    if (targetNode.left==null&&targetNode.right==null){
        delectNoChildenNode(targetNode);
    }else if (targetNode.left!=null&&targetNode.right!=null){
        delecWithTwoChildenNode(targetNode);
    }else {
        delectWithOneChildenNode(targetNode);
    }
}
private void delectNode(BalancedBinarySearchTreeNode targetNode) {
    if (targetNode.left==null&&targetNode.right==null){
        delectNoChildenNode(targetNode);
    }else if (targetNode.left!=null&&targetNode.right!=null){
        delecWithTwoChildenNode(targetNode);
    }else {
        delectWithOneChildenNode(targetNode);
    }
}

/**
 * 获取以当前节点为根节点的树中的最小值
 * 因为二叉树左子树永远要小于根节点，所以在树的最左侧的一定是最小的节点
 * @param node
 * @return
 */
public BalancedBinarySearchTreeNode getMinNode(BalancedBinarySearchTreeNode node){
    if (node.left == null){
        return node;
    }else {
        return getMinNode(node.left);
    }
}

/**
 * 获取以当前节点为根节点的树中的最大值
 * 因为二叉树右子树永远要大于根节点，所以在树的最右侧的一定是最大的节点
 * @param node
 * @return
 */
public BalancedBinarySearchTreeNode getMaxNode(BalancedBinarySearchTreeNode node){
    if (node.right == null){
        return node;
    }else {
        return getMinNode(node.right);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177

全部代码

package datestructure;

import java.util.prefs.NodeChangeEvent;

public class BalancedBinarySearchTreeNode {
    BalancedBinarySearchTreeNode parent;
    BalancedBinarySearchTreeNode left;
    BalancedBinarySearchTreeNode right;
    int val;
    public BalancedBinarySearchTreeNode (BalancedBinarySearchTreeNode parent,BalancedBinarySearchTreeNode left,BalancedBinarySearchTreeNode right,int val){
        super();
        this.parent = parent;
        this.left = left;
        this.right = right;
        this.val = val;
    }

    public BalancedBinarySearchTreeNode(int val){
        this(null,null,null,val);
    }

    public BalancedBinarySearchTreeNode(BalancedBinarySearchTreeNode node,int val){
        this(node,null,null,val);
    }

    /**
     * 获取当前树的高度
     */
    public int hight(){
        BalancedBinarySearchTreeNode left = this.left;
        BalancedBinarySearchTreeNode right = this.right;
        //获取左子树的高度，递归实现
        int leftHight = left==null?0:left.hight();
        //获取右子树的高度，递归实现
        int rightHight = right==null?0:right.hight();
        //当前树高度
        return Math.max(leftHight,rightHight)+1;
    }




    //单旋转
    /**
     * 单旋转-右旋
     *                  6                                               3
     *          3                 7                             1               6
     *      1        4                           =>                2         4      7
     *        2
     * 步骤两步：
     * 1.将3提为root.
     * 2.将3的右子树转移给6作为左子树
     * 应用场景：在插入、删除之前平衡二叉查找树是空树或平衡树
     *          插入或删除后才产生非平衡状态
     * @param node：6，插入节点到6之间非平衡
     */
    public BalancedBinarySearchTreeNode rightRotation(BalancedBinarySearchTreeNode node){
        BalancedBinarySearchTreeNode newRoot = node.left;
        newRoot.parent=node.parent;

        node.left = newRoot.right;
        newRoot.right.parent=node;

        newRoot.right = node;
        node.parent=newRoot;

        return newRoot;
    }

    /**
     * 单旋转-左旋
     * @param node
     * @return
     */
    public BalancedBinarySearchTreeNode leftRoatation(BalancedBinarySearchTreeNode node){
        BalancedBinarySearchTreeNode newRoot = node.right;
        newRoot.parent=node.parent;

        node.right = newRoot.left;
        newRoot.left.parent = node;

        newRoot.left = node;
        node.parent=newRoot;
        return newRoot;
    }

    //双旋转

    /**
     * 双旋转-左右旋
     *                    6                           6
     *              2           7    =>         4           7
     *          1      4                    2
     *               3                    1   3
     *
     *                     4
     *    =>        2           6
     *            1   3            7
     *
     *
     * 步骤：
     * 1.先对左子节点进行一次左旋
     * 2.再对根节点进行一次右旋
     * @param node
     * @return
     */
    public BalancedBinarySearchTreeNode leftRightRotation(BalancedBinarySearchTreeNode node){
        //在单旋的时候已经将节点的parent改过来了
        node.left = leftRoatation(node.left);
        BalancedBinarySearchTreeNode balancedBinarySearchTreeNode = rightRotation(node);
        return balancedBinarySearchTreeNode;
    }
    /**
     * 双旋转-右左旋
     */
    public BalancedBinarySearchTreeNode rightLeftRotation(BalancedBinarySearchTreeNode node){
        node.right = rightRotation(node.right);
        BalancedBinarySearchTreeNode balancedBinarySearchTreeNode = leftRoatation(node);
        return balancedBinarySearchTreeNode;
    }

    //二叉查找树搜索
    public boolean contains(int target){
        return contains(target,this)!=null;
    }


    public BalancedBinarySearchTreeNode contains(int target,BalancedBinarySearchTreeNode node){
        if (node==null){
            return null;
        }
        if (target>node.val){
            return contains(target,node.right);
        }else if (target< node.val){
            return contains(target,node.left);
        }else {
            return node;
        }
    }

    /**
     * 非平衡状态的判断，判断该节点属于LL、LR、RL、RR，并针对不同情况进行旋转平衡
     * @param node 从下向上第一次出现非平衡状态的节点
     */
    public void unbalancedState(BalancedBinarySearchTreeNode node){
        if (node.left.hight() == node.hight()){
            if (node.left.left.hight()==node.left.hight()){
                //LL
                rightRotation(node);
            }else{
                //LR
                leftRightRotation(node);
            }
        }else {
            if (node.right.left.hight()==node.right.hight()){
                //RL
                rightLeftRotation(node);
            }else {
                //RR
                leftRoatation(node);
            }
        }
    }

    //平衡二叉树删除
    /**
     * 删除节点没有子节点
     * @param node 要删除的节点
     */
    public void delectNoChildenNode(BalancedBinarySearchTreeNode node){
        //节点删除
        if (node.parent.left == node){
            node.parent.left = null;
        }else {
            node.parent.right = null;
        }
        //再平衡
        BalancedBinarySearchTreeNode tem = node;
        while (tem.parent==null){
            if (Math.abs(tem.left.hight()- tem.right.hight())>1){
                unbalancedState(tem);
               
            }
            tem = tem.parent;
        }
    }

    /**
     * 删除节点只有左节点或者右节点
     * @param node 要删除的节点
     */
    public void delectWithOneChildenNode(BalancedBinarySearchTreeNode node){
        if (node.parent.left == node){
            if (node.left != null) {
                node.parent.left = node.left;
                node.left.parent = node.parent;
            }
            else {
                node.parent.left = node.right;
                node.right.parent = node.parent;
            }
        }else {
            if (node.left != null) {
                node.parent.right = node.left;
                node.left.parent=node.parent;
            }
            else{
                node.parent.right = node.right;
                node.right.parent=node.parent;
            }
        }
        //再平衡
        BalancedBinarySearchTreeNode tem = node;
        while (tem.parent==null){
            if (Math.abs(tem.left.hight()- tem.right.hight())>1){
                unbalancedState(tem);
                
            }
            tem = tem.parent;
        }
    }

    /**
     * 删除节点既有左节点又有右节点
     * @param node 要删除的节点
     */
    public void delecWithTwoChildenNode(BalancedBinarySearchTreeNode node){
        if (node.left.hight()>node.right.hight()){
            BalancedBinarySearchTreeNode maxNode = getMaxNode(node.left);
            delectNode(maxNode);
            if (node.parent.left==node){
                node.parent.left=maxNode;
                maxNode.parent=node.parent;
                maxNode.left=node.left;
                node.left.parent=maxNode;
                maxNode.right=node.right;
                node.right.parent=maxNode;
            }else {
                node.parent.right=maxNode;
                maxNode.parent=node.parent;
                maxNode.left=node.left;
                node.left.parent=maxNode;
                maxNode.right=node.right;
                node.right.parent=maxNode;
            }

        }else {
            BalancedBinarySearchTreeNode minNode = getMinNode(node.right);
            delectNode(minNode);
            if (node.parent.left==node){
                node.parent.left=minNode;
                minNode.parent=node.parent;
                minNode.left=node.left;
                node.left.parent=minNode;
                minNode.right=node.right;
                node.right.parent=minNode;
            }else {
                node.parent.right=minNode;
                minNode.parent=node.parent;
                minNode.left=node.left;
                node.left.parent=minNode;
                minNode.right=node.right;
                node.right.parent=minNode;
            }
        }
    }

    /**
     * 删除节点
     * @param target
     */
    public void delectNode(int target){
        delectNode(target,this);
    }

    private void delectNode(int target, BalancedBinarySearchTreeNode node) {
        BalancedBinarySearchTreeNode targetNode = contains(target, node);
        if (targetNode.left==null&&targetNode.right==null){
            delectNoChildenNode(targetNode);
        }else if (targetNode.left!=null&&targetNode.right!=null){
            delecWithTwoChildenNode(targetNode);
        }else {
            delectWithOneChildenNode(targetNode);
        }
    }
    private void delectNode(BalancedBinarySearchTreeNode targetNode) {
        if (targetNode.left==null&&targetNode.right==null){
            delectNoChildenNode(targetNode);
        }else if (targetNode.left!=null&&targetNode.right!=null){
            delecWithTwoChildenNode(targetNode);
        }else {
            delectWithOneChildenNode(targetNode);
        }
    }

    /**
     * 获取以当前节点为根节点的树中的最小值
     * 因为二叉树左子树永远要小于根节点，所以在树的最左侧的一定是最小的节点
     * @param node
     * @return
     */
    public BalancedBinarySearchTreeNode getMinNode(BalancedBinarySearchTreeNode node){
        if (node.left == null){
            return node;
        }else {
            return getMinNode(node.left);
        }
    }

    /**
     * 获取以当前节点为根节点的树中的最大值
     * 因为二叉树右子树永远要大于根节点，所以在树的最右侧的一定是最大的节点
     * @param node
     * @return
     */
    public BalancedBinarySearchTreeNode getMaxNode(BalancedBinarySearchTreeNode node){
        if (node.right == null){
            return node;
        }else {
            return getMinNode(node.right);
        }
    }



}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326

参考文献

https://www.jianshu.com/p/2a8f2b3511fd

https://www.cnblogs.com/zhangbaochong/p/5164994.html

对借鉴的文章表示感谢，如有侵权，并非有意，请私信，本人将做出修改

本人能力有限，如文中存在错误，也欢迎指出，本人定将虚心聆听并改正

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/AllinToyou/article/detail/632108