路径规划——搜索算法详解（四）：A*算法详解与C++代码_a*搜索c++

前面几篇文章已经讲解了Dijkstra算法、Floyd算法、RRT算法，前面两种算法都是广度优先搜索算法，能够搜索到全局最优路径，但是时间复杂度较高，而RRT算法则是基于采样的路径规划算法，其特点主要是快，但是在有限时间内不能保证搜索路径为最优路径。截至到目前为止，上述学习的三种算法都是没有借助目标点的有效信息，导致搜索较慢，RRT*算法可以在采样上给予一定的启发（感兴趣的朋友可以去看看，看懂RRT后很好理解的）。

本文笔者将给大家介绍一个基础有效、且被广为运用的算法——A*算法，可以看作是启发式算法的开山代表作了，当然，本系列还会介绍基于此提出的D*算法、LPA*算法、D*lite算法，预计本周就可更新完搜索算法篇，掌握这个系列会让你初步入门路径规划算法的研究，希望对大家有所帮助吧！

A*算法解决的问题与Dijkstra算法一样，解决在静态环境中搜索最短路径的问题，其与Dijkstra算法的区别在于添加额外的目标点启发项。由于A*算法的重要性，本文代码部分将提供ROS+Rviz（C++）仿真环境下的代码，需要的自取就好，代码注释很详细，有任何问题或者笔者有所纰漏的地方大家直接在评论区留言就好，笔者看到会回复的。

一、A*算法流程（案例来自于深蓝学院课程，有点小贵，大家可以先看我的案例讲解）：

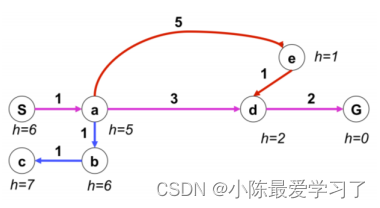
如上图所示，其中S为起点，G为终点，点与点之间的连线表示运动代价，如S-a运动代价为1，其含义与Dijkstra算法中的含义相同，现实含义可能表示两点之间的路程。而每一个路径点都具有一个启发值如S(h=6)，每一个路径点都具有一个启发值h，当目标点确定时候，可以通过特定的方式计算每一个路径点的启发值，如可以通过与终点的曼哈顿距离、欧氏距离来表示，可以根据实际情况来设计启发函数h。

1. 初始化：

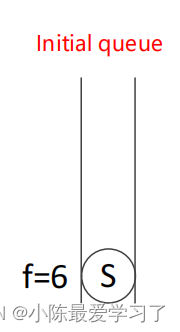
定义两个序列，其中一个为openlist M，用来存储待搜索的队列，一个为closelist N，存储已经搜索的队列，如上图所示，初始化时将起点加入openlist中，并计算其代价值f(s)=h(s)+g(s)，其中g(s)为s点距离起点的距离，而由于运动起点为其本身，g(s)=0，其启发项h(s)=6，故其f(s)=0+6=6，此时M={S(6)}、N={ }

2.排序与搜索（第一轮循环）：

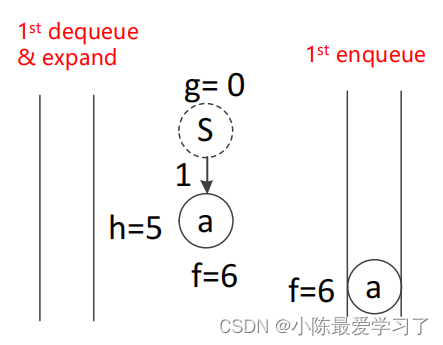
从openlist 并弹出f值最小的路径点），此时因为只有S一个元素，故选择将S放入到closelist N中，并计算与S连接的路径点（只与a有连接）的代价函数，并将其加入到openlist 中，此时与S相连的路径点为a，f(a)=h(a)+g(a)，此时g(a)为距离起点的距离：g(a) = 1，f(a) = 1+5 =6并将a加入到openlist 中，此时此时M={a(6)}、N={S}。

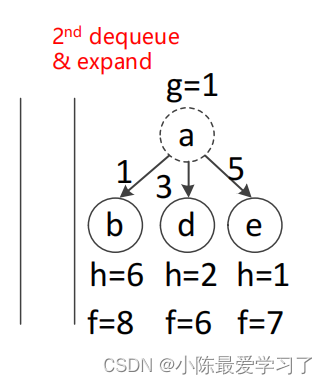
3.排序与搜索（第二轮循环）：

同理，此时在openlist M中弹出代价值f最小的路径点，此时只有a，故弹出a点，将a点加入到closelist N中，并搜索每一个与弹出节点a相连接的点，此处与a点连接的路径点有3个，分别为e、d、b，计算其代价函数，并加入到搜索队列M中。此时f(e)=h(e)+g(e)=1+5+1(5+1为距离起点的距离g(e))=7、f(d)=h(d)+g(d)=2+3+1=6、f(b)=h(b)+g(b)=6+1+1=8，此时M={e(7),d(6),b(8)}、N={S,a}。

4.排序与搜索（第三轮循环）：

此时在openlist根据代价值f进行排序，并且弹出f值最小的节点，此时f值最小的为d点，弹出d点将其加入到closelist中，计算与d相连接点G的f(G)=h(G)+g(G)=0(终点本身)+4+2=6，此时M={e(7),G(6),b(8)}、N={S,a,e}。

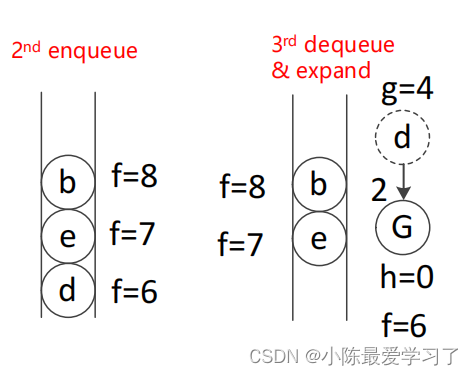
5.排序与搜索（第四轮循环）：

此时在openlist根据代价值f进行排序，并且弹出f值最小的节点，此时f值最小的为G点为目标点，弹出G点将其加入到closelist中，此次循环结束、N={S,a,e,G}。故生成的路径为S、a、e、G，在实际的算法中，A*算法流程如下，终止条件为openlist为空，当搜索不到终点时表示搜索失败，对于每一个节点记录其父节点，当搜索成功时进行回溯，得到最终路径。

初始化openlist和closelist；
将起点加入openlist中
if openlist不为空，则从openlist中选取f(n)最小的节点n：
    if 节点n为终点：
        从终点开始逐步追踪parent节点，回溯得到最终路径
        返回找到的结果路径，算法结束；
    if 节点n不是终点：
        将节点n从openlist中删除，并加入closelist中；
        遍历节点n所有的邻近节点：
            if 邻近节点m在closelist中：
                continue，选取下一个邻近节点
            if 邻近节点i也不在openlist中：
                设置节点i的parent为节点n
                计算节点i的f(i)
                将节点i加入openlist中

二、A*算法代码（C++）

代码已经上传到笔者的GITHUB中了，需要的朋友自取：

Adamaser/Path-Planning (github.com)