devbox
AllinToyou
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

五大经典算法-动态规划 及其算法应用_动态规划算法研究与应用

作者：AllinToyou | 2024-06-14 05:13:28

赞

踩

动态规划算法研究与应用

前言

整篇文章分析整个动态规划算法，什么是动态规划，及动态规划算法在字符串匹配中使用、分治法的差别点、动态规划优点；

概念

什么叫做动态规划(dynamic programming)，它是运筹学的一个分支，是求解决策过程最优化的数学方法。20世纪50年代数学家 R.E.Bellman等人 在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理，把多阶段过程转换为一系列单阶段问题，利用各阶段之间的关系，逐个求解，创立了解决这类过程优化问题的新方法-动态规划；应用在计算最短路径、库存管理、资源分配、设备更新、排序、装载等问题

特点

分析是由大到小，写代码是从小到大，计算过程中会把结果进行记录，最终结果在记录中找到

怎么去理解这个，从下面的基本思想中理解，我觉得大家就能理解了

基本思想 

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。

基本代码的实现

分治法一个简单的实现，之前用栈去解决斐波拉契数列这些问题，现在我们用动态规划去解决问题，用空间复杂度去换时间复杂度

原有栈的方式

  1.     public static int f(int n){
  2.         if(n==1 || n==2){
  3.             return 1;
  4.         }else{
  5.             return f(n-1)+f(n-2);
  6.         }
  7.     }

这种方式代码简单，但性能是非常不好的，一旦数据量大了之后这种方式时间消耗相当大，尤其是某些业务场景下，要求效率非常高；因此引入下面的代码动态规划，时间效率提高

  1. public static int sum1(int j) {
  2. 		int[] array = new int[j];
  3. 		array[0] = 1;
  4. 		array[1] = 1;
  5. 		for (int i = 2; i < array.length; i++) {
  6. 			array[i] = array[i - 1] + array[i - 2];
  7. 		}
  8. 		return array[j - 1];
  9. 	}

这就是通过动态规划去求最优化的解，这段代码的实现，小问题的结果相关联。分析过程是由大到小，而算法是由小到大的，通过存储空间记录，我们就能得到答案

总结

动态规划是求解具有某种最优性质的问题（子问题不是相互独立），并且和分治法一样都是将问题进行拆分，并且将拆分问题答案进行记录，从计算出最优的结果。明显可以看出动态规划是会多占用内存的，以空间复杂度来换取问题答案。

算法应用

最长公共子序列(Longest Common Subsequence,lcs)

这个应用在生活中应用的非常多，例如当前这个应用，就是对比数据的相似，截取公共部分，百度知道，相似度的比较:计算生物学DNA对比，图形相似处理,媒体流的相似比较,WEB页面中找非法言论等等

定义

一个序列A删除若干个字符得到新的序列B，而B就是A的子序列

 这样一删除字符过后就能获得到子序列

两个序列X和Y的公共子序列中，长度最长的那个，定义为X和Y的最长公共子序列

  例如X={A,B,C,B,D,A,B}，Y={B,D,C,A,B,A}则它们的lcs是{B,C,B,A}和{B,D,A,B}。求出一个即可。

这和顺序有关，相同的值的最大长度，并不管位置。怎么用动态规划去求出最长公共子序列，这就是我们动态规划去研究的，除了动态规划，我们还有什么方法，那当然是穷举法，这个最恶心，在于拿着一个字符一个字符，一位一位的去比对，就会找到，但性能糟糕，没法用的。

算法分析

我们用下面例子进行分析

X={B,D,C,A,B,A}，Y={A,B,C,B,D,A,B}则它们的lcs是{B,C,B,A}和{B,D,A,B}。求出一个即可。

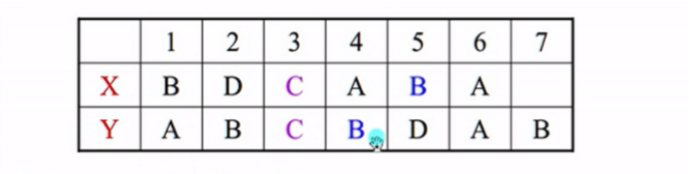
我们用上面 的来表示 ，比如Y4=B X4=A  通过这样来分析lcs求解 

  •  字符串X,长度m,从1开始计数
  • 字符串Y,长度n,从1开始计数
  • Xi=<x1,x2,...,xi>表示X序列的前i个字符(1<=i<=m)
  • Yj=<y1,y2,...,yj>表示Y序列的前j个字符(1<=j<=n)
  • LCS(X,Y)为字符串X和Y的最长公共子序列,其中的一个解为Z=<z1,z2,....zk>
  •   注意:LCS(X,Y)（最长公共子序列）其实为一个集合,Z为一个解

就像我在刚才分析那样，最长的公共子序列有多个解，所以是一个集合来存储，而Z就是其中的一个解

思路解析

首先取两个字符串的末尾进行取一个字符对比

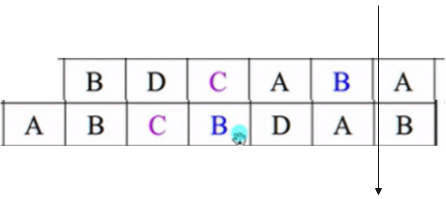
 如果两个字符串不相等则有两种情况下面

  • 第一种X去除末尾字符进行对比

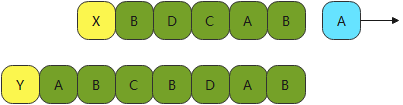
  •  Y去掉末尾字符进行对比

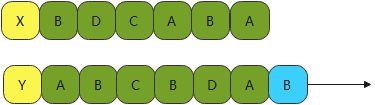
 如果最后一位是相同的，那就是下面种情况

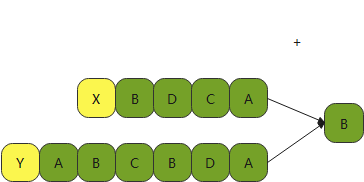
 就这样重复往前步骤，就是这样找到了最长子公共序列

 最终得到的结论就是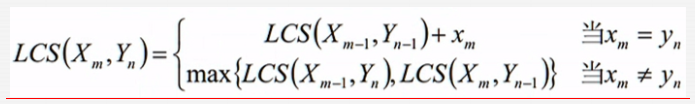

 这个结论

  • 如果 最后一位相等，上面个公式，最长子公共序列加上相同的xm 或者 ym
  • 如果最后一位不相等，取xm-1和yn的公共子序列和 xm和yn-1的公共子序列的最大的公共子序列，这就能找到最长公共子序列

代码分析与编码

我们需要建立一个二维数组，相同的取左上加1,不同取上和左的最大值 ，这也是从上面

 首位都填空字符串，都不填位置，

 

 按照规则不断填，就能填出上面的值，然后就能找到公共子序列的长度。这就是动态规划的算法，从前往后推，记录好之前的数据，不断往前推，而在去取长度。有规律，只要数据加长一位时，则表明相同的字符。

我们继续寻找最长的公共子序列，从后往前推，这样就能找到一个公共子序列，ABCB ,在反过来就是了 和BADB 

 先从建立一个小方法开始

  • 写一个字符长度不同的时求最大值
  1.     public static int max(int a,int b){
  2.         return (a>b)?a:b;
  3.     }
  •  建立核心方法getLCS 并创建一个二维数组 传入 x 和y字符串，用于后面的操作
  1.  char[] s1=x.toCharArray();
  2.         char[] s2=y.toCharArray();
  3.         int[][] array=new int[x.length()+1][y.length()+1];
  •  然后就按照我之前构造的数组，做个数据填充，当然也可以不填充
  1.  for (int i = 0; i < array[0].length; i++) {
  2.             array[0][i]=0;
  3.         }
  4.         for (int i = 0; i < array.length; i++) {
  5.             array[i][0]=0;
  6.         }
  • 使用动态规划的方式填入数据，一格一格判断字符串 这里需要减一次比较 ，s1和s2是原字符，相等因为在数组上数据是从1开始的，所以不能按照数组来。就已经能得到刚才的矩阵了
  1.  for (int i = 1; i < array.length; i++) {
  2.             for (int j = 1; j < array[i].length; j++) {
  3.                 if(s1[i-1]==s2[j-1]){//如果相等，左上角加1填入
  4.                     array[i][j]=array[i-1][j-1]+1;
  5.                 }else{
  6.                     array[i][j]=max(array[i-1][j],array[i][j-1]);
  7.                 }
  8.             }
  9.         }
  • 然后继续往前找结果，去找到数据，先搞一个栈进行存储，因为是反过来
Stack result=new Stack();
  • 往前找数据
  1.  int i=x.length()-1;
  2.         int j=y.length()-1;
  3.         while((i>=0) && (j>=0)){
  4.             if(s1[i]==s2[j]){
  5.                 result.push(s1[i]);
  6.                 i--;
  7.                 j--;
  8.             }else{//注意数组和String中的位置有一位差
  9.                 if(array[i+1][j+1-1]>array[i+1-1][j+1]){
  10.                     j--;
  11.                 }else{
  12.                     i--;
  13.                 }
  14.             }
  15.         }

这样求最长公共字串我们就能找到了，动态规划就能实现了

KMP算法（改进的字符串匹配算法）

kmp算法和lcs算法不同点在于撒，也就是lcs算法，在匹配两个字符串的相似度，而kmp算法也就是我们在java种字符串进行匹配，只有字符串在目标字符串中能找到时，才算是ok的。

是一种改进的字符串匹配算法，由由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为克努特-莫里斯-普拉特操作（简称kmp算法）

他的时间复杂度能达到o（m+n） 是相当快的， KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。

采用穷举法则是下面的情况

 这是大家都能想通的方式，但可以想象，我们jdk肯定不能这么简单的，那效率速度有多慢。

还有一种

  

将目标串先进行循环 对比的方式，最后两位和前面两位相同，然后下次倒退，倒退到前ab然后继续对比，这样也很消耗 性能，效率也很慢的。

接下来介绍kmp算法如何做的

既然利用动态规划的特性，需要用一个数组来帮我们存储帮助我们找到回退的次数的 假设为倒退数组next

规则

第一步 使得next[i]=j

第二步 i++

第三步判断i和j的字符是否相等

i和j的字符相等 j++; 

i和j的字符不同则 j=next[j-1];

下面继续分析字符串

  •  首先进行复制一个相同模式串，第一步先在next数组中填0，i从1开始，j从0开始，遇到不同，直接j++

  • 第二次遇到数据相同了，先赋值next，在j++

这样以此类推下去 

 j是不断在前三个做循环，然后 这样记录下了循环的动作，而i不断增加；

最后这个数组得到的值的特点，进行对比

 这种情况可以看到几个值相同的情况，这种，我就能发现在对比字符串时，如果对比不成功，就对比到退到哪一个节点，这就能很好的节约时间

 这个算法就是这样不断对比往里面推，一旦遇到不同 j=next[j-1]  这是j的值如果为3就跳到第三位字符上，截取过后与目标字符串进行对比，以达到成功的情况

代码实现

首先匹配串找到next数组建立kmpnext算法

  1.    public static int[] kmpNext(String dest){
  2.         int[] next=new int[dest.length()];
  3.         next[0]=0;
  4.         //开始推出next
  5.         for(int i=1,j=0;i<dest.length();i++){
  6.             //3
  7.             while(j>0 && dest.charAt(j) != dest.charAt(i)){
  8.                 j=next[j-1];
  9.             }
  10.             //1
  11.             if(dest.charAt(i)==dest.charAt(j)){
  12.                 j++;
  13.             }
  14.             //2
  15.             next[i]=j;
  16.         }
  17.         return next;
  18.     }
  • 这里做的是，先创建next数组
 int[] next=new int[dest.length()];
  • 重复下面的规则

第二步 i++

第三步判断i和j的字符是否相等

i和j的字符相等 j++; 

i和j的字符不同则 j=next[j-1];

第一步 使得next[i]=j

  1.             //判断字符是否相同的或者不同
  2.             while(j>0 && dest.charAt(j) != dest.charAt(i)){
  3.                 j=next[j-1];
  4.             }
  5.          
  6.             if(dest.charAt(i)==dest.charAt(j)){
  7.                 j++;
  8.             }
  9.             // 
  10.             next[i]=j;

然后实现kmp算法 

  1.  for(int i=0,j=0;i<str.length();i++){
  2.             while(j>0 && str.charAt(i) != dest.charAt(j)){
  3.                 j=next[j-1];
  4.             }
  5.             if(str.charAt(i)==dest.charAt(j)){
  6.                 j++;
  7.             }
  8.             if(j==dest.length()){//结束
  9.                 return i-j+1;
  10.             }
  11.         }

结束条件，最后通过i-j+1就能找到需要的位置，这个思路是相当精妙的;记录到快速找到左边连续的点。用来做回退的。

总结

动态规划算法应用非常广泛的，学习它的思路，在开发过程中，大家都有一个好的解决方法的思路，不要只是就用什么穷举法呀，大家都能想到，但是效率非常低，在项目中是不能使用的，小数据量还行，一旦数据量增大，时间非常长，希望这篇动态规划，通过原理和应用上讲解，能有成长。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/AllinToyou/article/detail/716556
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号